這篇文章是我這學期在大學學習遊戲設計的一些筆記摘錄和心得的彙總，分為上下兩篇，包含了一些遊戲設計理論文章的概念和我自己製作的桌遊的實踐手法。如果你想以一種更加系統和理論的方式瞭解遊戲設計的話，那麼這篇文章中介紹的概念和方法相信可以幫到你、並指引你入門遊戲設計。

閒話少說，讓我們直接步入正題吧！

遊戲的交互性

遊戲作為娛樂媒介的一大特色就是玩家能夠與其互動並得到反饋。而在設計領域中，遊戲設計可以被視為廣義交互設計中的一個大分支，而交互設計中的一些基礎定義也能在遊戲中發現共鳴的地方。

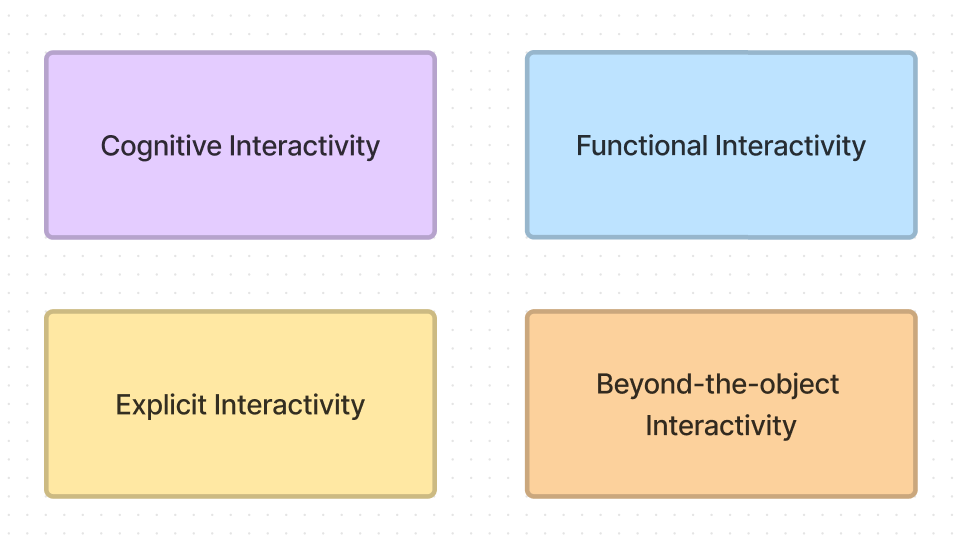
4類交互行為

在交互設計中，我們可以將交互行為分為4大類：認知交互（cognitive interactivity）、功能交互（functional interactivity）、內置交互（explicit interactivity）和文化交互（beyond-the-object interactivity）。其中和遊戲本體關聯最大的是內置交互，也就是遊戲中內置的分支、隨機事件、動態模擬以及所有對遊戲內互動產生貢獻的程序。對於視覺小說來講，內置交互就是玩家可以通過點擊推進劇情的行為所產生的互動感。

通過點擊和選擇推動劇情繼續

與內置交互對立的是功能交互。它們都屬於遊戲本身帶來的互動，但內置交互強調的是遊戲軟件，功能交互則突出遊戲硬件的反饋。如果你的手柄用起來非常舒服，按鍵下去不會有明顯的延遲，顯示屏上的文字UI清晰易懂、分辨率也很棒，那麼這個遊戲的功能交互就到位了。

Switch的手柄給予了特殊的功能性，但720p的顯示屏經常被詬病

當前兩種交互十分有效的情況下，認知交互和文化交互會更優秀的發揮價值。認知交互的定義是情緒上的共情，也就是遊戲內容如何打動玩家；文化交互則代表了一些玩家在體驗過遊戲後自發形成的粉絲團或者文化二創形式。

分支與選擇

那麼，在瞭解完基礎的4中交互行為後，讓我們聚焦在內置交互，並展開聊一聊最為普遍的一個例子——分支和選擇（choice-making）。交互作品通常會給予觀眾選擇的權力，而選擇本身可以分為“

微觀選擇”和“宏觀選擇”。

微觀選擇存在於當下，是玩家在當前遊戲狀態下做出的小決策；宏觀選擇存在於過去和未來，是玩家考慮到整體的遊戲走向做出的大方針。在國際象棋中，玩家操控棋子走的每一步都是一個微觀選擇，而玩家對整體棋局的把控和預判則是宏觀選擇。

國際象棋是一種經典的策略性遊戲

“行為-結果”模型（action > outcome unit）可以幫助我們剖析每一個遊戲中的選擇。這個模型共有5個步驟：

選擇出現前的遊戲背景和鋪墊
選擇在玩家心中的可能性（桌遊中的抽卡堆暗示著選擇的可能）
選擇呈現給玩家的形式（二選一、擲骰子、棋子行動……）
選擇導致的結果（以及對後續選擇的影響）
結果呈現給玩家的方式（比如說對話了導致好感度增加）

順帶一提，每個步驟都涵蓋了內在事件（internal event：遊戲系統內部對選擇的處理和接收）或外在事件（external event：選擇呈現給玩家）的其中一種。

舉一個簡單的例子。在《女神異聞錄5》（Persona 5）中，玩家扮演的怪盜在潛入反派的宮殿時總會遇到巡邏的敵人，這就引出了打或逃的選擇。想象一下，你正在一個宮殿中探索，然後發現前方走廊不遠處出現了一個來回巡邏的敵人，這個敵人的出現就是“選擇出現前的遊戲背景和鋪墊”。

遇到了敵人

現在你停下了腳步，開始思考應對它的方法：你可以直接衝上前以極快的速度開啟戰鬥，但也可能冒著被敵人發現使戰鬥開始陷入debuff的狀態；你可以尋找周圍的掩體躲避，並通過在不同掩體間跳轉逐步逼近敵人，以先手偷襲buff的狀態開啟戰鬥；你也可以直接衝破敵人防線（會被它發現，但你確信你跑的更快），或者通過掩體悄無聲息地繞過敵人。

在這段心理活動中，掩體和走廊代表著“選擇在玩家心中的可能性”，因為這兩種元素引申出了不同的選擇；而跑（鍵盤中的wasd鍵）和躲（鍵盤中的space鍵）則是“選擇呈現給玩家的形式”。“選擇導致的結果”有兩種：開啟戰鬥或者成功逃離；“結果呈現給玩家的方式”則是戰鬥界面或者後續的場景區域（對於戰鬥來說會產生“偷襲產生開場buff”或“被發現產生開場debuff”這兩種小的結果呈現形式）。

機制-動態-美學

MDA模型（Mechanics - Dynamics - Aesthetics）是一種適用於遊戲分析的理論模型，將遊戲分成“機制”（Mechanics）、“動態”（Dynamics）和“美學”（Aesthetics）三個部分。

讓我們首先簡單地定義一下這三個詞彙。“機制”代表了能讓遊戲可以遊玩所必要的所有成分，包含了遊戲規則、遊戲器材、遊戲場所和遊戲元素。如果我們將遊戲本身類比成一個系統的話，“機制”就是對系統的完整的介紹。

與此相對，“動態”則詮釋了遊戲中的行為、事件和遊戲運行時產生的現象和反饋。一言以蔽之——“遊戲在被遊玩時都發生了些什麼？”另一方面，可以認為“機制”的運作催生了遊戲中豐富多彩的“動態”。

最後，遊戲中的“美學”是玩家體驗遊戲時所產生的情感波動。遊戲如何進行決定了它如何激發玩家不同的情感反應。對於“機制”來說，它是一直存在的；對於“動態”來說，它只存在於遊戲運行時；而對於“美學”來說，它的存在與否取決於玩家如何體驗手頭的遊戲以及如何將遊戲中的“動態”轉換為更生活化的情感觸動。

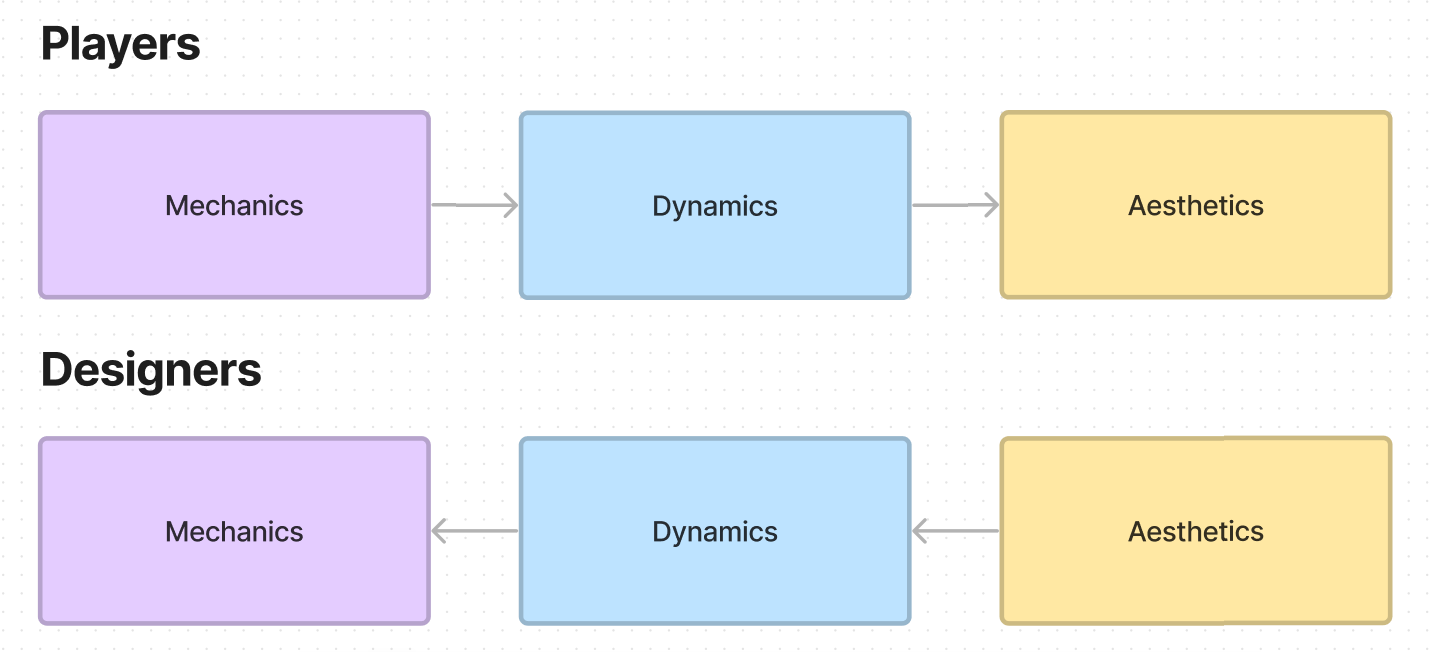
每一個玩家在玩遊戲時基本都是從認識“機制”開始，到體驗不同的“動態”，最後產生相應的“美學”情感。但是，對於遊戲設計師來講，他們必須反其道而行之，首先思考自己想傳遞給玩傢什麼樣的情感，再思考什麼樣的“動態”能激發出這種情緒，最後再設計出能承載這些“動態”的“機制”。遊戲“美學”具有很多類別，在這裡我挑取了“戲劇性”（Game as Drama）這一種類深入展開一下。

戲劇性的美學

在介紹具體的實現戲劇性美學的方法論前，我想先引入“戲劇性曲線”（Dramatic Arc）的概念。“戲劇性曲線”是對一個好故事的起承轉合的視覺表示，是一種服務於故事的美學模型。下圖是一個標準的“戲劇性曲線”，遊戲的極點（Climax）發生在頓悟（Realization）的時候，即遊戲的勝負已經可以預見、所有的不確定感全部消除的那一刻。

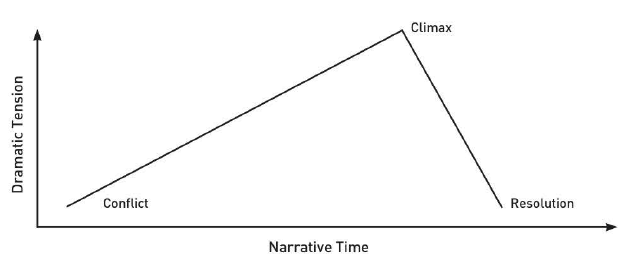
Dramatic Arc

在遊戲中，敘事本身並非是預先譜寫好的，而是由遊戲事件催生出的產物；遊戲事件構建了一個又一個衝突，而戲劇性元素則在這些衝突中誕生。那麼，如何在遊戲中植入一條完美的“戲劇性曲線”呢？這就引出了兩大法寶：“不確定性”（Uncertainty）和“必然性”（Inevitability）。

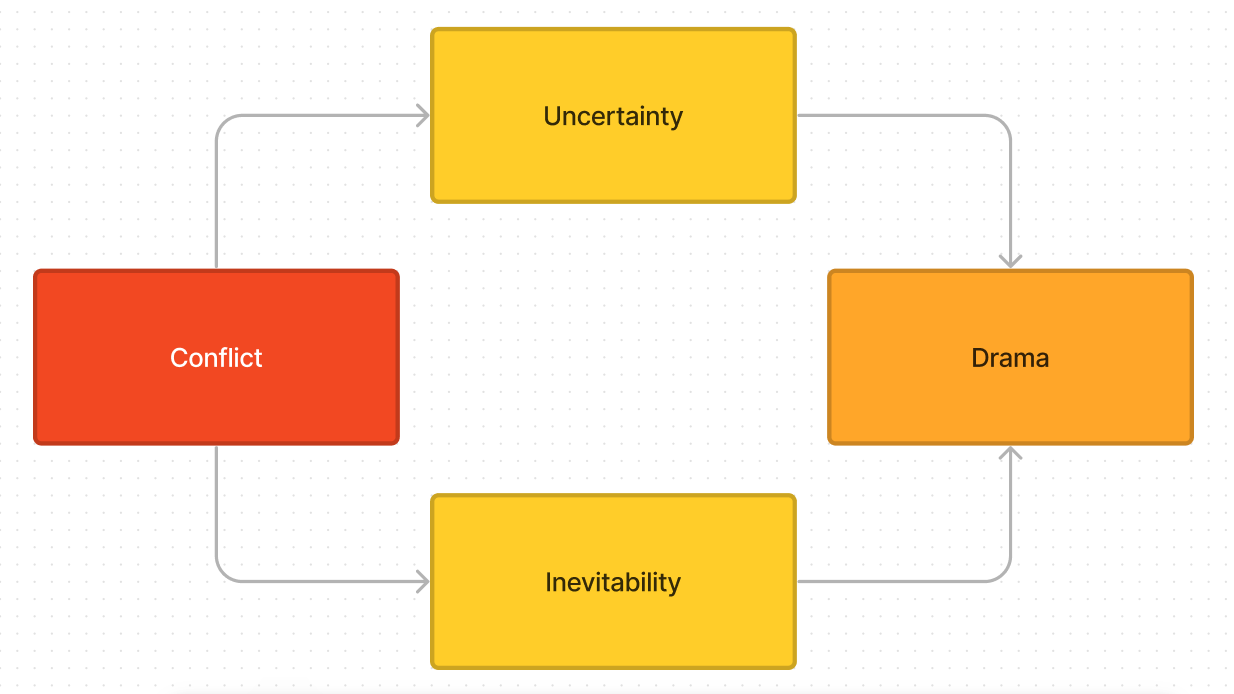
衝突通過“不確定性”和“必然性”創造戲劇性

首先，這兩個法寶可不是對立的。不確定性表示了遊戲中的隨機性和結局未定前的未知感；正是因為這種感覺玩家才能投入到遊戲中，因為勝負未定，一切都還有可能。必然性表示了遊戲終將走向結束的命運；如果一個遊戲沒有結束條件，那麼它就將永遠持續下去，而玩家們則會因為沒有目標而迷失在遊戲之中。一言以蔽之，遊戲終將結束、但勝負仍未分曉的感覺是我們所追求的。

方法論：不確定性

以下是一些常用的構建不確定性的方法：

反饋循環（Feedback Loop）：分為負反饋循環和正反饋循環，可以用來進行遊戲平衡，具體的介紹將在後續部分介紹，敬請期待。

在馬里奧賽車中，落後的玩家會獲得更強力的道具來幫助他們反超，而領先的玩家獲得的道具基本毫無用處，這就是負反饋循環所造成的結果。在RPG遊戲中，玩家擊敗怪物後會獲得成長，等級上升或是更多的技能解鎖，正反饋循環使得玩家在遊戲過程中越變越強。

排名越前道具越次

逐步加碼（Escalation）：在遊戲過程中，遊戲比分的變化速度逐漸加快，意味著遊戲結束前比開始時有更多的風險點。

在雙人搶答問題的遊戲中，假設總共有7題，第一題1分，第二題10分，第三題10分，以此類推。玩家1可能在遊戲前期次次搶答成功拿到了大多數的分數，但是因為後面題目的分值更大，勝負便仍未確定。積攢的優勢可能隨著遊戲推進迅速轉變，劣勢的玩家也有翻盤的機會，這就是逐步加碼的魅力。

隱藏能源（Hidden Energy）：遊戲中的潛在的得分手段，來源於玩家對得分系統的不完整的認知。

在賽車遊戲中，假設存在一個超級加速踏板，玩家踩下後會使賽車瘋狂加速，但這個踏板只能用5秒，也就意味著玩家需要決策需要在何時何地最有效的運用這個隱藏能源來最大化自己的利益。

賽車遊戲中的渦輪加速

戰爭迷霧（Fog of War）：模擬了玩家只能觀測到眼前的事物而非整個世界本身，通過有限的信息獲取製造了不確定性。

使用戰爭迷霧限制玩家視野

減速障礙（Decelerator）：一種在遊戲後期減緩玩家速度和優勢的障礙，改變遊戲的規模和節奏。

在真人闖關遊戲中，假設在遊戲末尾加入一個高臺，並從高臺下垂一張網，闖關者必須從網爬上高臺以進行後續的挑戰，也就意味著後面的闖關者會和第一位開始攀爬的闖關者逐漸縮短距離，因為攀爬是垂直方向的，而移動是水平方向的。這會給闖關者們帶來虛假的希望。請注意，不確定性不一定非得是真實的遊戲狀態的改變，也可以是催眠玩家的假象。

垂直的攀爬讓玩家誤以為縮小了距離

優勢提現（Cashing Out）：將遊戲比分重置為0，寬恕落後參賽者的分數差距，給每個選手一個獲勝的機會，無論多麼不可能。

以輪次為框架的遊戲中，每一輪比賽結束後，所有的優勢都變成了一個簡單的結果——排名第一的玩家會獲得獎盃。在這之後，所有的道具被重置，所有的失誤被清除，玩家們在下一輪對抗中以完全公平的狀態開始。在另一種情況下，每輪的得分可以被轉換成下一輪的數值上的優勢（比如更高的傷害），這也構成了一種正反饋循環。

方法論：必然性

“不確定性”讓玩家思考“誰會贏”，“必然性”則會讓玩家思考“我們什麼時候知道這個結果”。對於“必然性”來說，並沒有五花八門的方法，正所謂大道至簡。我們唯一擁有的王牌，叫做“**倒計時”（ticking clock）。“倒計時”是不可逆的過程，提供了一種時間的前進感，同時在遊戲中加入了時間限制的這個變量。

桌遊《禁閉島》（Forbidden Island）提供了一種典型的“倒計時”機制。這是一款多人合作類的桌遊，玩家需要在不同方形紙片的島嶼上移動他們的棋子。每一個輪次結束後一些隨機的島嶼就會擱淺或沉沒；而玩家的目標是在所有島嶼沉沒前，前往特定的島嶼收集一定數量的元素，併到達停機坪島嶼成功逃離這片禁閉島嶼。

桌遊《Forbidden Island》

在這個遊戲中，“倒計時”的機制分為兩個層面。在宏觀層面上，遊戲中具有水位線這個數值：每一輪結束後根據玩家會抽取接下來會沉沒的島嶼卡牌，而一定幾率下他們可能抽到水位上漲卡牌，這就會提升水位線。當水位線提升到最高值時，遊戲立即結束，玩家會直接被海洋淹沒。在微觀層面上，每一輪都會有新的島嶼變成擱淺或者沉沒狀態；當玩家首次抽到一個島嶼卡牌時，那個島嶼會變成擱淺狀態。玩家還是可以經過擱淺的島嶼並進行搶救使其恢復到正常狀態，但如果玩家在島嶼擱淺時再次抽取到了同樣的島嶼卡牌，該島嶼就會沉沒並移除遊戲地圖。

《禁閉島》通過宏觀和圍觀的兩種“倒計時”機制，成功塑造出了遊戲的目標感和緊迫感，防止了玩家悠哉遊哉地對待遊戲，將遊戲的節奏進一步強化。可以說，當你想去設計一款遊戲時，不妨考慮一下如何在遊戲中加入“倒計時”的機制，這總歸是一個不錯的潤滑油。接下來，我將會簡要介紹一下我是如何從《禁閉島》中提取靈感，並在我設計的桌遊中加入“倒計時”的。

案例：《蟑螂戰爭》

大學的宿舍生活總是充滿歡樂，而學生和宿管的勾心鬥角更是一直被津津樂道。你，作為一個已經在宿舍裡呆滿一年即將搬走的大學生，需要應對宿管最後的宿舍考察。你環顧了一下房間，發現你和你的好舍友已經將宿舍清潔忘了個一乾二淨，你們很確信如果宿管前來搜查宿舍，角角落落的蟑螂定會被逮個正著。正在你們打算做最後的補救時，敲門聲響了，啊偶，看來只能走一步看一步了。

《Roach Wars 蟑螂戰爭》是由兩名學生和一名宿管進行的合作對抗類遊戲，學生需要齊心協力阻止宿管在他們的宿舍中找到蟑螂，而宿管則需要拼盡全力發現更多的蟑螂（可能算績效的年終獎？）。遊戲的主戰場是學生的宿舍內，由4*4的地板方片組成，方片的正面風平浪靜，但背面可能就會是一個噁心的蟑螂。遊戲採取回合制的行動，玩家每回合有3次行動機會，學生可以選擇移動到不同地板上、翻開地板消滅蟑螂、或者交換兩個地板的位置，而宿管除了移動外，如果翻開地板時發現了蟑螂，那麼就會獲得一分，累積查到3只蟑螂後遊戲結束，宿管勝利。

嗯，我是不是漏說了一個很重要的部分？哦對，那麼學生應該如何才能取得勝利呢？這就是我們運用到“倒計時”機制的環節了。一開始我們的想法是製造一個最粗暴的“倒計時”，即在7個回合後若宿管仍未找到3只蟑螂，學生就會獲得遊戲的勝利。在測試的時候我們發現了一個問題：我們必須讓整個宿舍產生一種動態性，因為16塊地板很容易就會被全部翻完。這就像“井字棋”（tic tac toe）一樣，9個位置很快就會被填滿“o”或者“x”，遊戲失去了一種更新的感覺。於是，我們決定在每回合結束後，從一疊地板牌堆中抽取新的地板並放置到宿舍中隨機的地板之上（通過投骰子決定放置的具體位置）。新的地板上可能也會有新的蟑螂，給予了整個遊戲一直變化的動態。

能不能讓遊戲的動態更加多樣呢？當然可以，這就需要遊戲中常用到的特殊道具的出場了。2張地板被我們替換成了食物卡，一旦翻開食物卡，回合結束時抽取地板牌堆時就得多抽一張。其次，我們規定了地板牌堆中蟑螂的概率是 2/3，也就是說玩家翻開的食物卡越多，下一回合新增的蟑螂數量也會更多。這個改動平衡了學生和宿管的實力，給予了宿管正反饋循環（翻開的卡越多，越有可能翻到食物卡，而食物卡則會讓局勢偏向自己），使得遊戲後期的局勢越來越緊張。嗯，這或許也是一種“減速障礙”的體現啊。

改動到這裡，我們對一開始的那個粗暴的“倒計時”機制已經不太滿意了，因為我們發現了一個能更好表現倒計時的元素——地板牌堆。既然每回合結束後都必須抽取地板牌堆中的地板更新宿舍的話，那麼把牌堆中的數量卡成大概7個回合左右的量不就行了？如果只是固定7個回合結束遊戲的話，可能一些食物卡還沒翻開，地板牌堆也可能會有很多的剩餘。但是，如果我們直接將抽完地板牌堆作為遊戲結束的條件的話，遊戲的平衡性會更容易把控，因為所有的地板都不可避免地會進入到遊戲中。

未完待續

講到這裡，你是否對一些遊戲設計的概念有了瞭解和認識呢？正所謂知行合一，概念通常是苦澀的，如同茶葉一般。需要熱水泡開才能完全理解茶葉的清香。《Roach Wars》這個項目讓我掌握了“倒計時”機制的運用和迭代，而也希望這篇文章能幫助你更方便地理解我用了半學期才掌握的概念。在文章的下半部分，我將其深入講解遊戲中的反饋循環和湧現式模擬這兩個概念，敬請期待！