一 問題的符號學轉換
1.1
上篇文章從符號學理論的視角,系統地探討、定義了什麼是遊戲不平衡的實質。然後,一個新的問題就出現了。從嚴格意義上說,現實中的很多競技活動,特別是電競遊戲,其實際的對局,運行在一個不平衡的規則系統之上,因此嚴格來說,它是不平衡的對局。但是,在通常情況下,這種不平衡,似乎也並不影響現實競技活動的正常運行,也不影響比賽最終會決勝出實力更強的那一方。
1.11 按照上篇文章的理論定義,幾乎所有的電競遊戲,其自身的遊戲規則系統,都是一個不平衡的符碼規則系統。因此,從理論的嚴格意義上來說,這些電競遊戲的對局,必然就是一場不平衡的對局。
1.12 但是,儘管運行於一個不平衡規則系統之上,看起來,電競比賽似乎也並沒有完全受到這種不平衡的嚴重干擾和破壞,以至於,正常的比賽都無法進行下去。進而,也沒有影響到勝負的正常判定,即實力更強的獲勝,實力更弱的失敗。
1.13 當然,說完全沒有影響,那是不可能的。因為比賽的運行,即比賽文本的生產,是運用符碼規則來進行生產的。長久以來,每一個電競遊戲,關於平衡性的爭議都從未斷過。只不過,從長期、宏觀來看,這種爭議,並沒有嚴重到競技比賽無法正常進行下去的地步。
1.14 那麼,問題就來了,按照上篇文章所說,平衡不絕對,就是絕對不平衡。那麼在絕對不平衡的情況下,為什麼競技比賽活動還能正常運行下去呢?

1.2
這個問題,是上篇文章所遺漏的一個點。因為上篇文章,僅僅只是在探討規則系統的問題,沒有涉及到遊戲系統實際運行的問題,即比賽文本生產活動的問題。對這個問題的探討,需要從上述理論的視角,將這個問題細化。也就是說,要把這個問題本身進行一個符號學轉換,從而將其轉換為符號表意的問題。
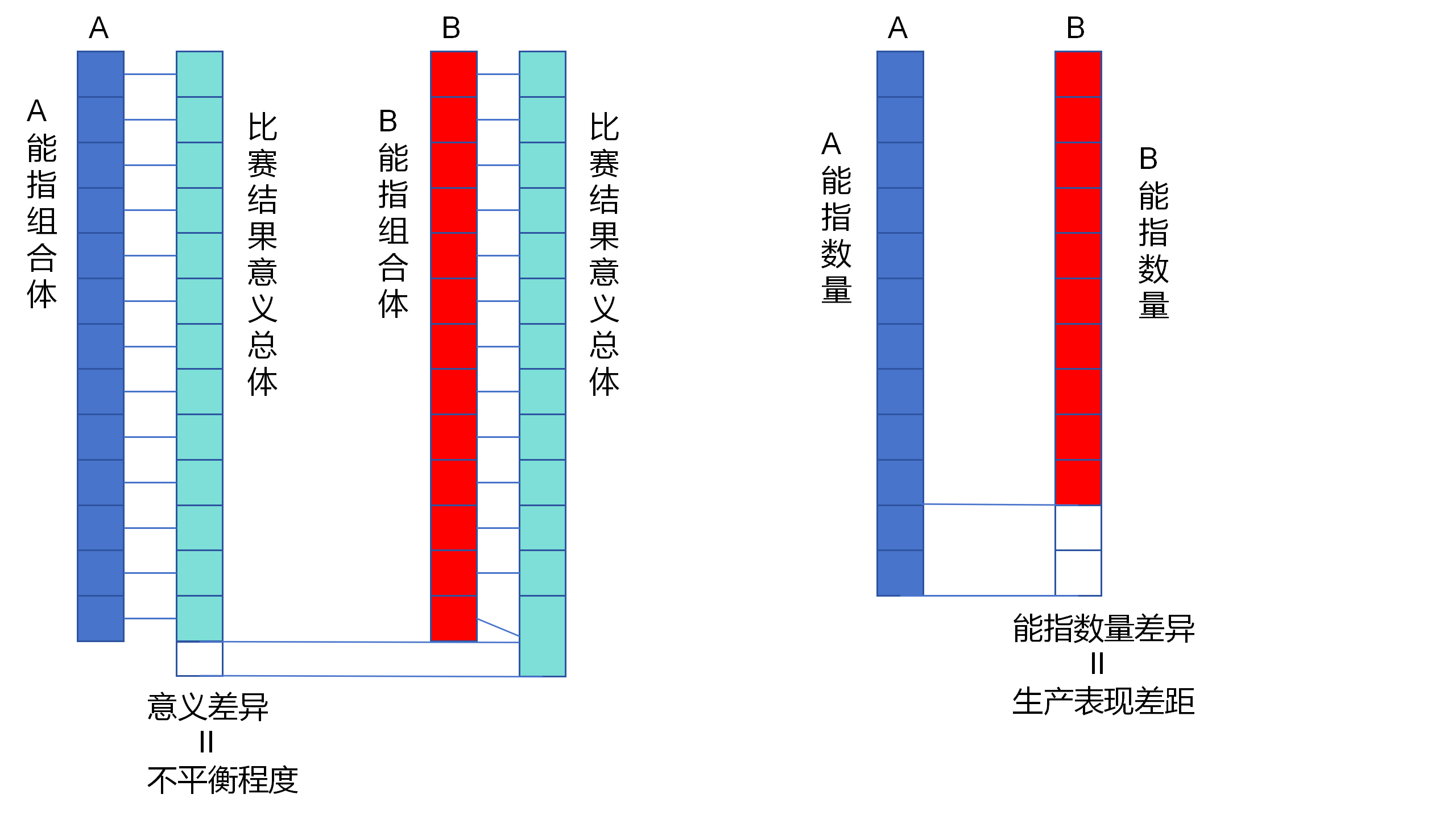
1.21 按照前述理論,平衡性問題,實質上是生產表現和比賽結果意義之間的關係問題。進而,也就是能指數量和意義總體之間的關係問題。所謂遊戲平衡,就是後者完全是由前者所決定的,完全是由前者所生產出來的。而只有在能指單元的意義完全同一的情況下,這一點才會成立,才能是平衡的。
1.22 在這個基礎之上,這個問題就可以被轉換為:在不同一的符碼規則系統下,什麼樣的因素,才會使得不同參賽者的能指數量的相同不同,與比賽結果意義之間的相同不同,彼此是一致的。也就是說,符碼規則的不同一,不會影響相同不同的能指數量,生產出相對應、相一致的 相同不同的比賽結果意義。
二 條件1:不平衡程度<能指數量差距
2.1
這裡的問題關鍵,不在於量上的差異,而在於質上的差異。也就是說,只要不平衡所導致的量的差異,沒有造成質的變化,那麼這個不同一的符碼規則系統,就不會影響到能指數量和比賽結果意義之間的決定關係。也就是說,符碼規則系統不會代替參賽者,決定比賽結果意義之間的相同不同關係。
2.11 所謂質,就是不同比賽文本的能指數量之間的相同不同關係,相應的不同比賽結果意義之間的相同不同關係,即相同還是不同。所謂量,就是能指數量,相應的比賽結果意義的具體內容(依不同遊戲而定,例如跑步比賽的XX秒)。
2.11 不同一的符碼規則系統,不會影響能指數量本身。因為能指的數量,與規則系統無關,它完全是在每一次競技活動中,由參賽者第一次生產出來的全新產品。規則系統絕不會設定每一場比賽中只能生產多少能指,無論規則系統平衡與否,能指的數量,都完全是由參賽者自身來決定的。
2.12 而每一個能指所對應的意義,就完全是預先被設定在符碼規則系統中的。作為預先存在,參賽者無法改變它。因此,符碼規則所能影響的,就是所有意義單位綜合構成的比賽結果意義。
2.13 在電競遊戲中,玩家所輸入的每一個動作指令,其對應的效果,完全是預先被設定在遊戲規則系統中的固定性存在,玩家無法改變它。而玩家所輸入的指令數量,以及所有指令的組合,則是每一次遊戲活動中的全新產物。
2.2
設定兩個參賽者,有著相同的生產表現,即組合了相同數量的能指。如果兩者的符碼規則系統不同一,那麼其對應的比賽結果意義,必然就是不相同的。相同的能指數量,對應著不相同的比賽結果意義。
2.21 這時,可以看一下兩個不相同的比賽結果意義,彼此之間的差異有多大。如果差異越大,則說明符碼規則系統的不同一程度,也就越大。也就是說,符碼規則系統的不平衡程度,也就越大。如此,兩個比賽結果意義之間的差異程度,就成為了規則系統不平衡程度的丈量器。不過,這必須是在兩邊能指數量完全相同的條件下,才能成立的。
2.22 但是,在實際情況中,即便是基本平衡的競技遊戲,平局也是不常見的。因此,參賽者所生產的能指數量,一般情況下,不太可能完全相同。通常會一方多於另一方,從而分出勝負。

2.3
在這裡,就出現了兩個差異關係:一個是在能指數量相同下,兩個比賽結果意義之間的差異,一個是參賽者之間能指數量的差異。前者代表符碼規則系統的不平衡程度;後者代表參賽者之間生產表現的差距,也就是通常所說的實力差距。
2.31 如果一個遊戲的不平衡程度,可以測量的話,那麼在確定的符碼規則系統下,這個不平衡程度,就會是一個確定值。在有了這個確定值之後,就可以把它和能指數量的差距相比較,也就是和不同參賽者之間生產表現的差距相比較。
2.32 如果能指數量的差距大於不平衡的值,即參賽者之間的實力差距,大於遊戲的不平衡程度。那麼即便遊戲不平衡,參賽者之間的實力差距,就可以抵消cover掉遊戲不平衡所帶來的影響。
2.33 因為,雖然遊戲不平衡,但是由於實力差距太大,能指數量的差距就會太大。大到一定程度,能指數量少的那一方,即便有意義單位不同一的加持,其對應意義所構成的比賽結果意義,也無法追趕上能指數量多的比賽結果意義。從而,比賽結果意義之間的不同,誰勝誰負的結果,本質上並沒有改變。能指數量的不同,與比賽結果意義的不同,仍然是一致的。這就是前面所說的,不平衡所導致的量的差異,沒有造成質的變化。
2.34 反過來,如果能指數量的差距小於不平衡的值,即參賽者之間的實力差距,小於遊戲的不平衡程度。那麼,參賽者之間的實力差距,就無法抵消遊戲不平衡所帶來的影響。在這種情況下,實際對局就將是不平衡的對局,即規則的不平衡轉換為實際上的不平衡。
2.34 不平衡能不能影響比賽結果,取決於,不平衡程度是否大於選手之間生產表現的差距。如果大於,則會決定比賽結果,如果小於,則不會決定。
2.4
公式1:不平衡程度≥生產表現差距→實際對局=不平衡
公式2:不平衡程度<生產表現差距→實際對局=平衡
2.41 這就是為什麼,在現實的競技活動中,特別是電競比賽,儘管經常運行在一個不平衡的規則系統之上,但是卻並不影響競技比賽的正常運行,不影響勝負結果的正常判定。
三 條件2:意義差值方向=能指數量差距方向
3.1
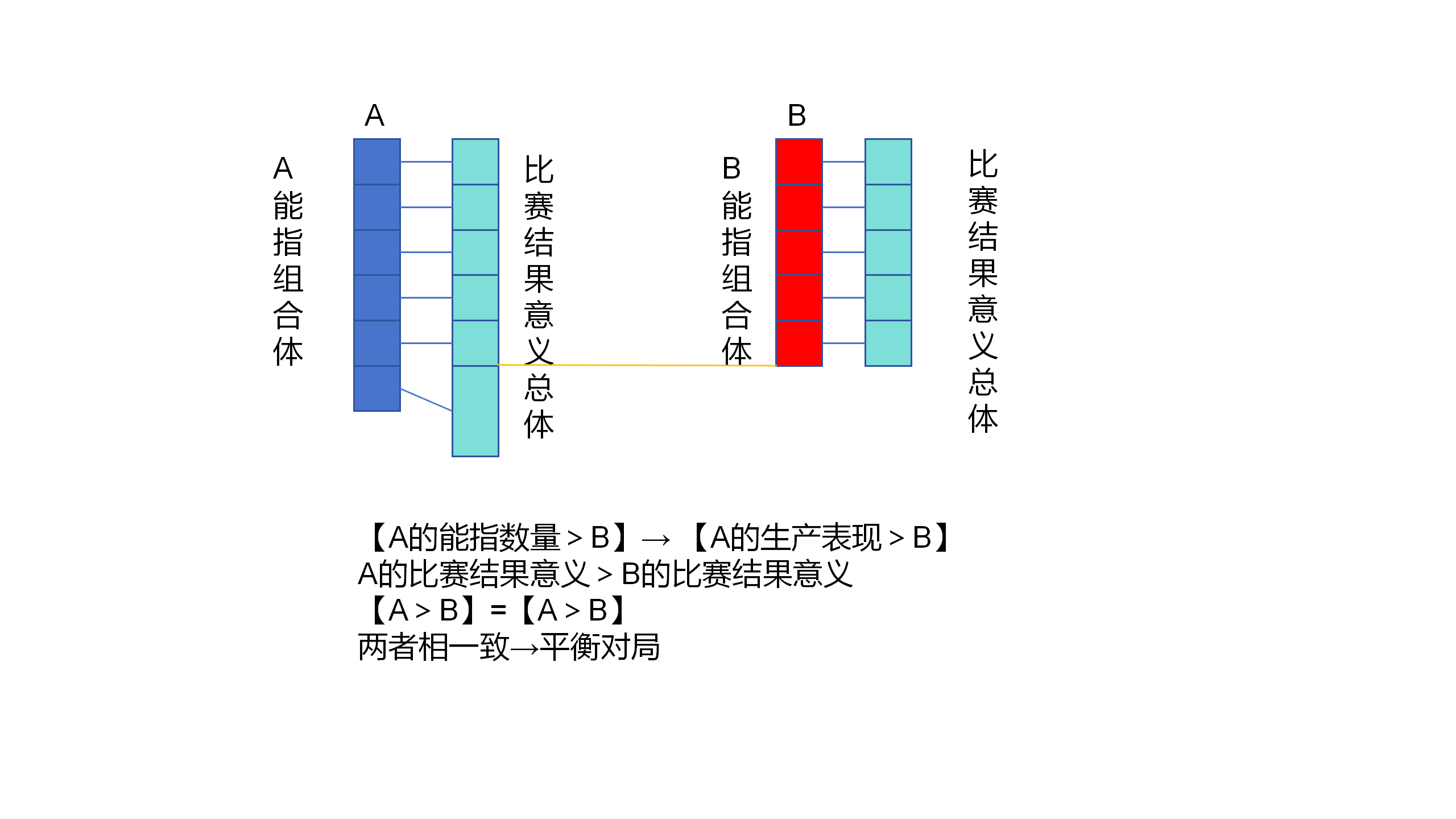
當然,還有一種可能的因素,那就是在意義層面上,雙方所有能指對應的意義,綜合起來而構成的比賽結果意義,恰好與雙方的生產表現是相一致的。也就是說,就這場對局而言,規則不平衡的方向,與勝負的方向,是一致的。規則不平衡所不利於的那一方,恰好就是生產表現更弱的那一方,也就是失敗的那一方。
3.11 例如,A生產了6個能指,B生產了5個能指。如果符碼規則是同一平衡的,那麼毫無疑問,A是獲勝者。
3.12 但是,如果符碼規則是不平衡的,並且這種不平衡有利於A,不利於B。也就是說,在這個遊戲的特定規則設定中,B文本中的能指,其所對應的意義,要弱於、差於A文本中的能指,所對應的意義。進而,B文本所構成的意義總體,差於A文本所構成的意義總體。
3.13 那麼在這種情況下,符碼規則的不平衡,也就不會影響到A理所應當的獲勝,B理所應當的失敗。也就是說,在這種情況下,參賽者最終生產出來的比賽結果意義總體,與自身的生產表現,是一致的。
3.2
在這種情況下,現實對局的平衡,實質上也是一種偶然。由於不平衡方向和生產表現差距的偶然一致,這一場對局實現了平衡性。但下一場,就不必然如此了。
3.21 並且,由於這兩者方向上的一致,符碼規則系統不同一、不平衡的實質,被完美地掩蓋了起來。在表面的遊戲過程中,在表面上的比賽場面和形勢中,根本察覺不到任何的失衡之處。
3.22 通俗來說,就是雙方的巨大實力差距,掩蓋了獲勝者在規則上所佔據的不公平優勢。
3.3
不同於上一種條件,是兩個差值關係之間的大小對比關係,是關係中的關係,頗為複雜。這個條件,更為簡單一些,它只是要求兩個差值在方向上一致,要求是同一個方向。
3.31 一個是意義單位的差值,一個是能指數量的差值。
3.32 不同參賽者背後的符碼規則系統,其中每一個能指對應著一個意義,作為構成比賽結果意義總體的基本意義元素,它是意義單位。在不平衡的遊戲中,不同參賽者的意義單位之間,存在著差距。可以稱之為意義差距。
3.33 在比賽過程中,不同參賽者所生產出來的能指數量也是有差距的,即能指量差距。
3.34 意義差距和能指量差距,兩者在方向上必須是一致的,是同一個方向。即獲勝者的意義單位和能指數量,均大於失敗者。
四 條件3:失衡無法察覺
4.1
當然,還有一種可能的情況,那就是在客觀實際上,不平衡確實對比賽的運行,產生了影響。不同一的符碼規則系統,在實際上確實代替了參賽者,生產出了比賽結果意義,從而決定了不同比賽結果意義之間的相同不同關係。
4.2
然而,這種導致失衡的影響干擾,同樣也是有量的程度區分的。
4.21 如果這種量的程度很小,比較微弱,在直接的感知上,無法被直接察覺到。或者說,在表面的感知呈現中,人們察覺到了一些疑似的異樣,但是對於是否失衡,無法準確把握和判定,沒有定論。那麼即便在客觀上確實是不平衡的對局,依然會被當作是一場平衡的對局來處理。勝利者的勝利,會被看作是理所應當的勝利,失敗者的失敗,會被看作是理所應當的失敗。
4.3
體育比賽中的很多爭議判罰,就屬於這種情況。特別是那種影響了比賽最終走向的關鍵判罰。
4.31 在這種情況下,對於判定裁判的判罰是否正確合理,各路人馬各執一詞,一部分人認為判罰正確合理,一部分認為判罰值得商榷,甚至完全錯誤。由於無法準確判定,因此,這場對局,只能被當作一個平衡的對局來處理。
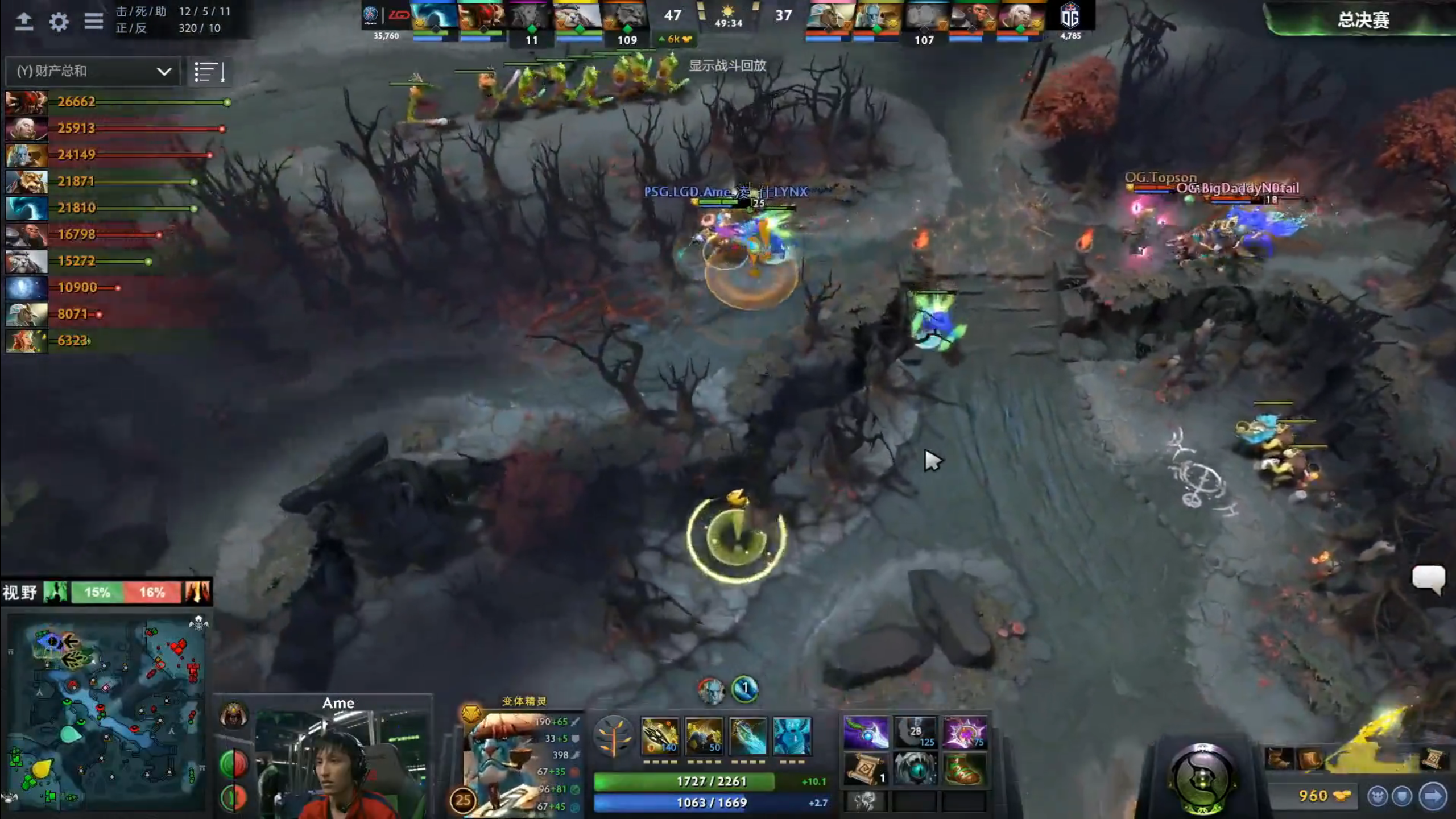
4.32 在電競中,也出現過類似的情況。在TI8決賽LGD和OG的第四局當中,由於遊戲出現了BUG,ame的水人喪失了一部分敏捷屬性。毫無疑問,這個BUG在這場對局中確實造成了一些不平衡,讓ame水人所對應的意義單位,差於OG方英雄所對應的意義單位。但是,這個不平衡對於比賽的走向,究竟產生了多大的影響,是否大到足以替換了參賽者ame,從而讓作為規則的BUG本身,來決定了最終的比賽結果呢?這是很難說的。要準確測量這個BUG是否決定性地影響了最終的比賽結果,將會是一個非常浩大的工程量。在這種沒有直接覺察到、無法確定的情況下,我們只能認為,OG是理所應當的獲勝,LGD是理所應當的失敗。
五 跑步比賽的能指和意義
5.1
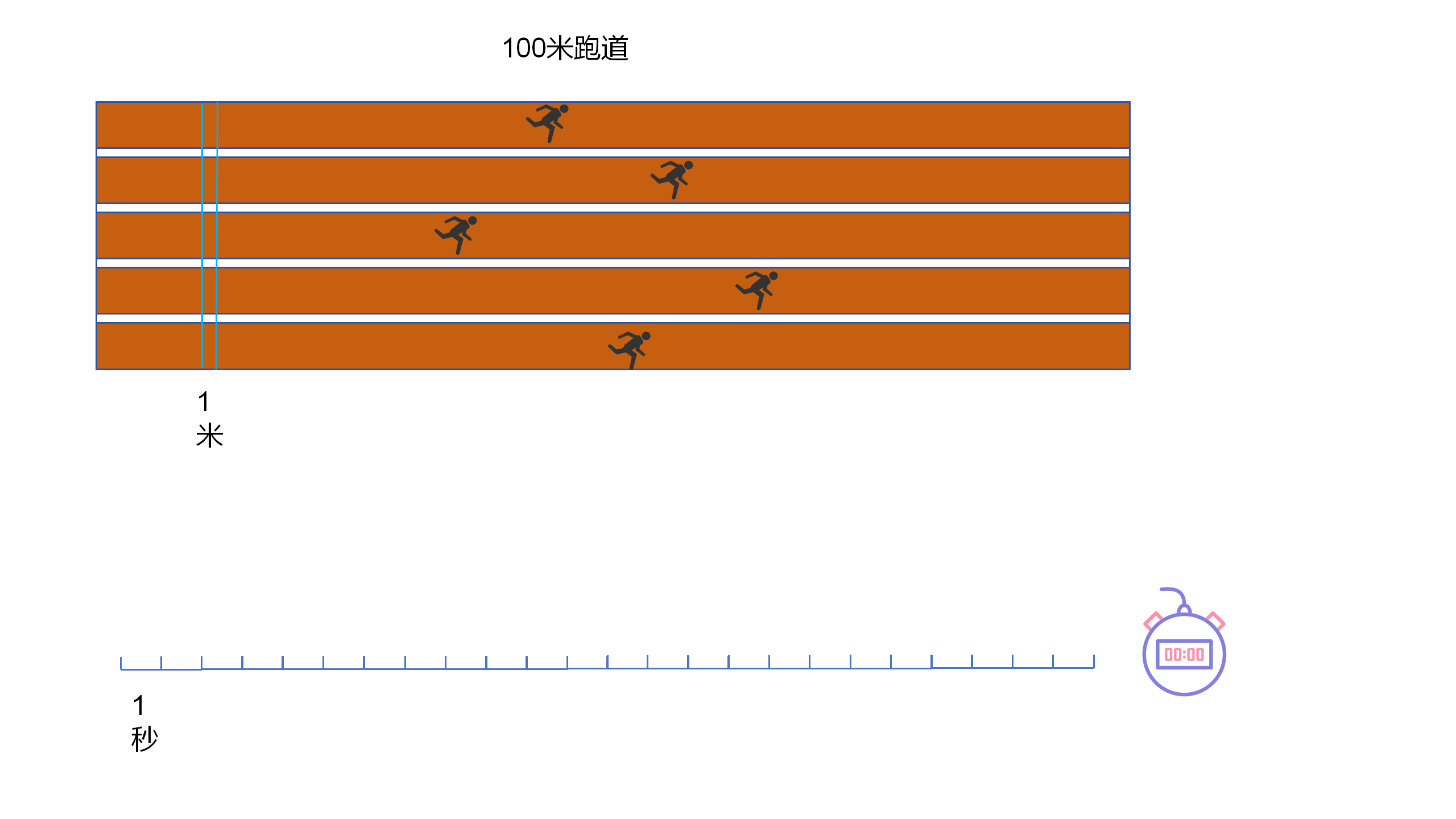
以跑步比賽為例,100米比賽,A和B兩個賽跑選手。首先要確定跑步遊戲的能指和意義。
5.11 毫無疑問,賽跑選手自身在進行跑步運動時的視覺形式,就是跑步比賽文本的能指的自然形式。那麼,跑步比賽的意義單位是什麼呢?毋庸置疑,賽跑運動是一個基本平衡的競技遊戲。那麼,按照理論,其能指所對應的意義單位,就必然是同一的。跑步遊戲中的同一意義單位,究竟是什麼呢?
5.12 首先從作為比賽結果意義的XX秒說起。設定A為獲勝者,100米用10秒跑完,B為失敗者,100米用12秒跑完。在這裡,作為跑步比賽結果的東西,並不僅僅只是單純的時間總量,而是時間總量和100米距離的對比關係,共同構成一個整體不可分的比賽結果意義。這個10秒、12秒,是針對100米距離長度而言的10秒、12秒,脫離這個100米的距離,單獨的時間總量,無法構成跑步比賽的結果意義。這就是跑步這個遊戲的特殊之處所在。
5.2 意義單位
如果進一步細看,我們會發現,在這個結果意義中,距離是相同的,差異在於時間。然而,將兩個結果意義進行對比,獲勝者所生產的時間總量,要少於失敗者所生產的時間總量,這似乎有悖於上述理論中的邏輯。在平衡的遊戲規則系統之下,獲勝者之所以獲勝,是因為生產出了更多數量的能指,進而所綜合構成的意義總體,勝於對方。按照這個邏輯,這個意義總體,如果是作為量化的存在,也應該是在量上多於失敗者,才能符合勝於對方的邏輯。但是,這裡的比賽結果意義,是時間和距離的對比關係,而不是單獨的時間量。因此,必須要更進一步,把這個對比關係本身,更進一步展開為一個單獨的量。
5.21 很簡單,就是用距離量除以時間量。因為跑步比賽,就是看賽跑選手用多長的時間,跑完這個預先確定的距離總量。通過相除,兩者的對比關係本身,就得出了一個作為單獨量的對比結果,這個結果就是通常所說的速度。在速度這個單獨量中,終於可以看到,獲勝者在量上是多於失敗者的。100÷10=10m/s,這是A的速度為1秒10米;100÷12≈8.3m/s,這是B的速度為1秒8.3米。10米>8.3米,因此A獲勝。由此,把比賽結果意義轉換成為了一個單獨的量化存在。而通過這個速度概念的揭示,也表明了跑步競技的實質:跑步競技遊戲,其所真正比拼的東西,是速度。因此,賽跑選手在跑步比賽中,所生產出來的比賽結果意義,其實是速度。速度這個概念本身,就包含了距離和時間兩個意義內容。何為速度?單位時間與時間內位移距離的對比值。
5.22 這兩個速度,作為時間總量和距離總量的對比值,是由時間單位1秒和距離單位1米,綜合構成的。而構成A速度的1秒和1米,構成B速度的1秒和1米,都是完全相同的同一個東西。是同一個1秒時間單位和1米距離單位,構成了A和B各自的速度。這是因為,10m/s中的1秒和1米,和8.3m/s中的1秒和1米,有著完全相同的時間運動幅度和距離幅度,即有著完全相同的意義內容。因此,跑步遊戲的同一意義單位,就是1秒和1米。
5.3
那麼,按照理論,在比賽過程中的每個1秒和1米,其所對應的跑步運動的視覺形態,就是這個同一意義單位所對應的單個能指。每一個這樣的單個能指,就共同構成了A和B各自的跑步文本。A生產出了更多量的這個能指,因而先於B到達終點線,獲得勝利。
5.31 然而,在這個視覺形態中,似乎找不到有任何量化的存在。因為這個視覺形態,單純只是一個純粹的視覺感知呈現,是一個純然的自然存在。在這種純粹自然性存在中,前一秒的跑步運動和下一秒的跑步運動,並沒有被感知所區分開來,是絕對的連續性視覺印象。而表意的能指顯然不會是這樣,表達前一秒的能指,和表達下一秒的能指,絕對不能混同。因此,在這種純粹的連續感知印象中,這種視覺形態,還並沒有被設定為能指。進而,它還不是一種量化的存在。

5.32 但是,按照前面的理論,意義才是能指的本體,在表意關係中,能指的自然形式是無關緊要的。因此,這裡可以通過符號學轉換,懸置掉跑步運動的自然形式。既然按照理論原則,每一個能指,都對應於同一的1米和1秒。那麼,就拋開現實世界中不同賽跑選手的千姿百態的跑步動作,把它們全部設定為完全同一的視覺形式。甚至可以更為極端,全部將正在跑步的運動員,處理為一個方塊。整個100米比賽,就是幾個方塊的位移過程。因為在這裡,跑步運動的視覺上的自然形態,是根本無關緊要的東西。
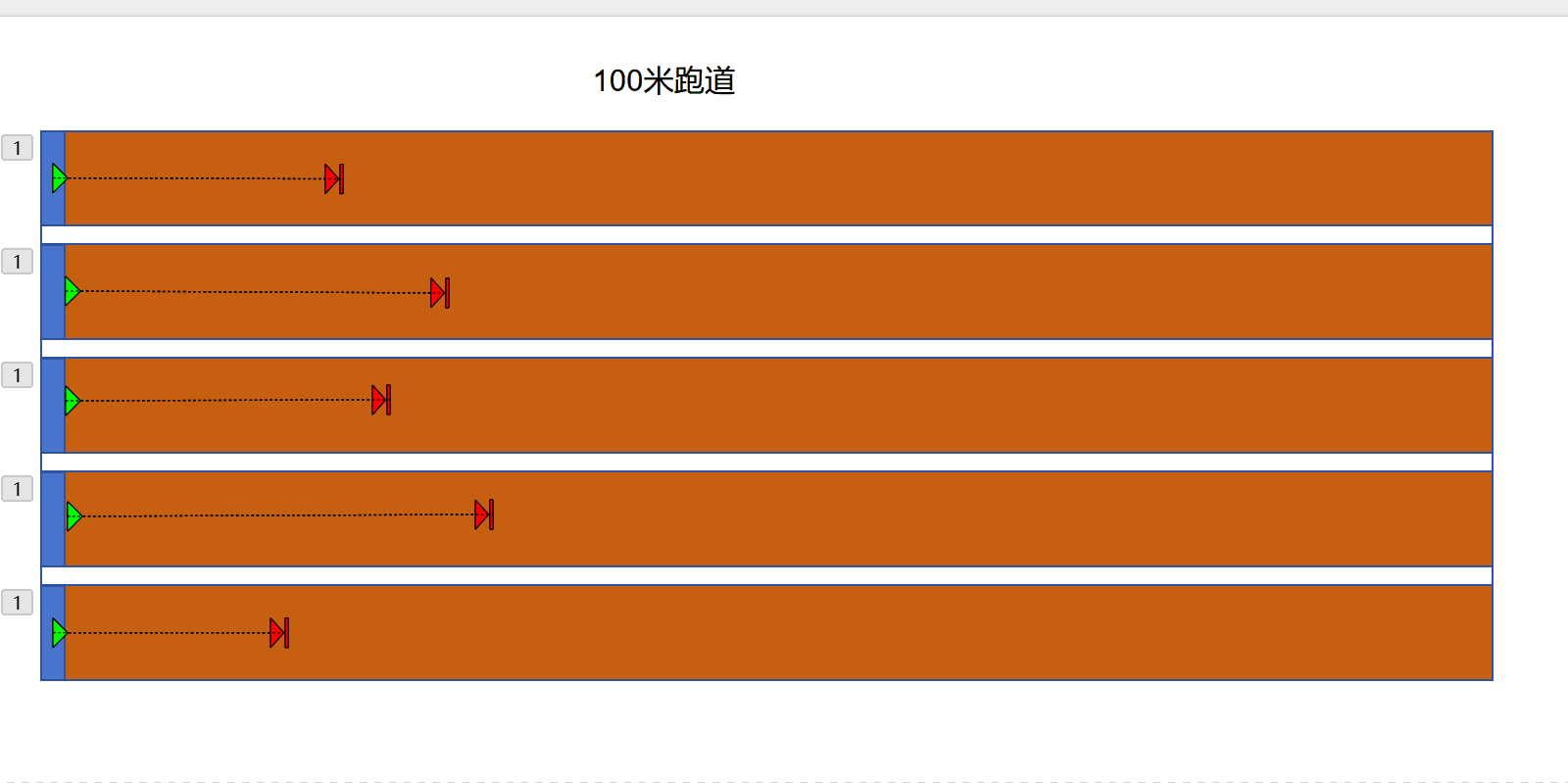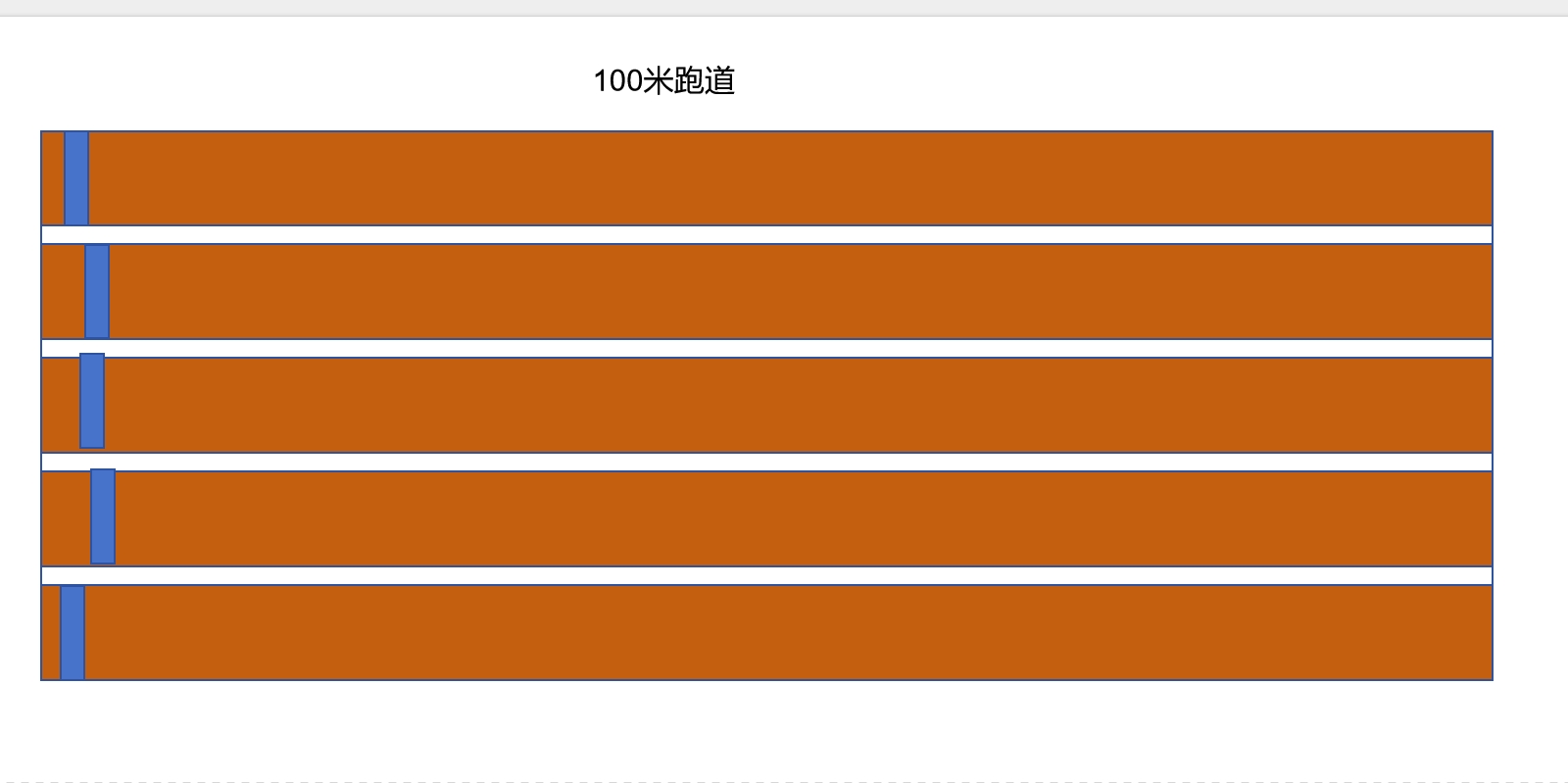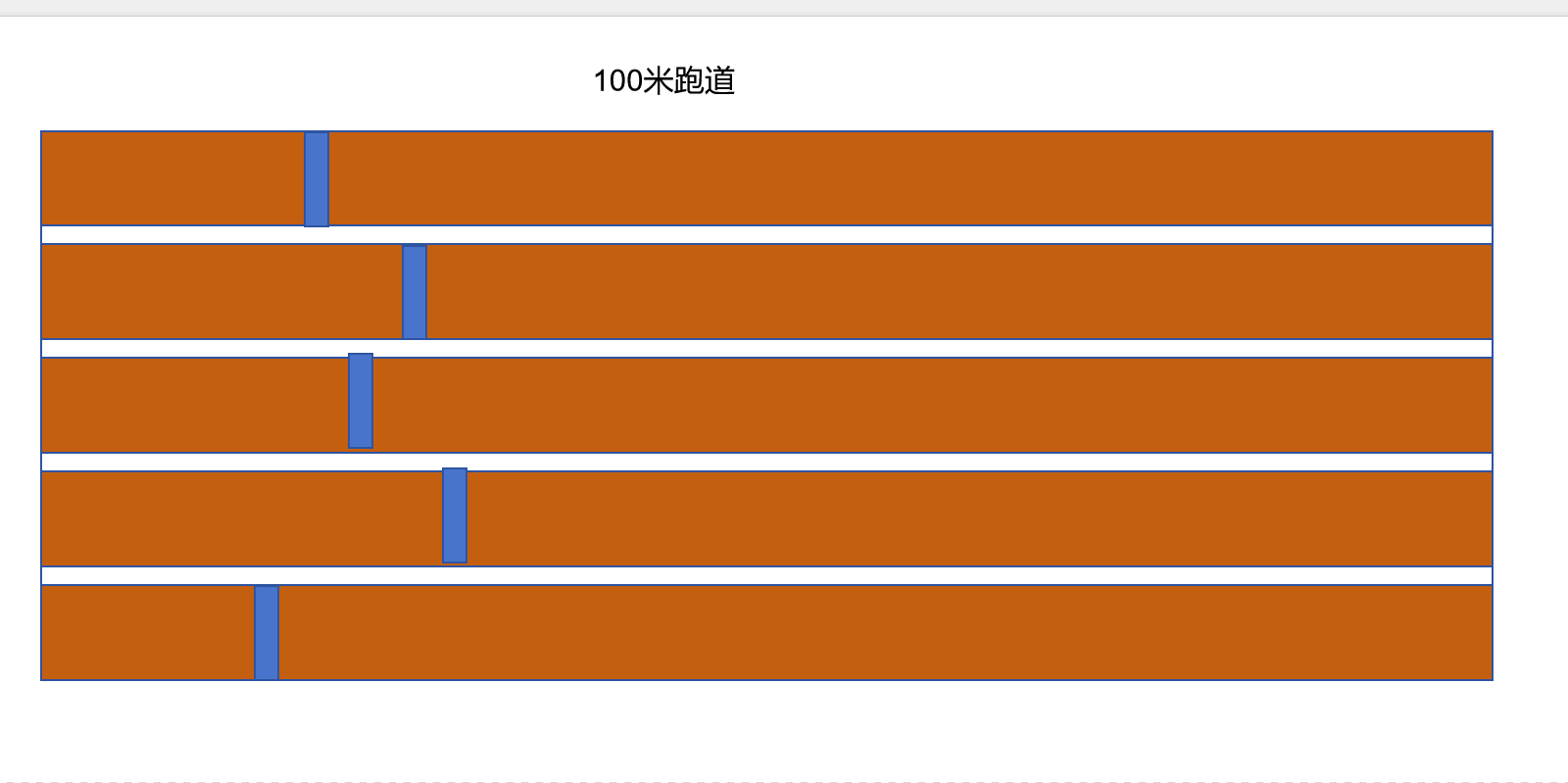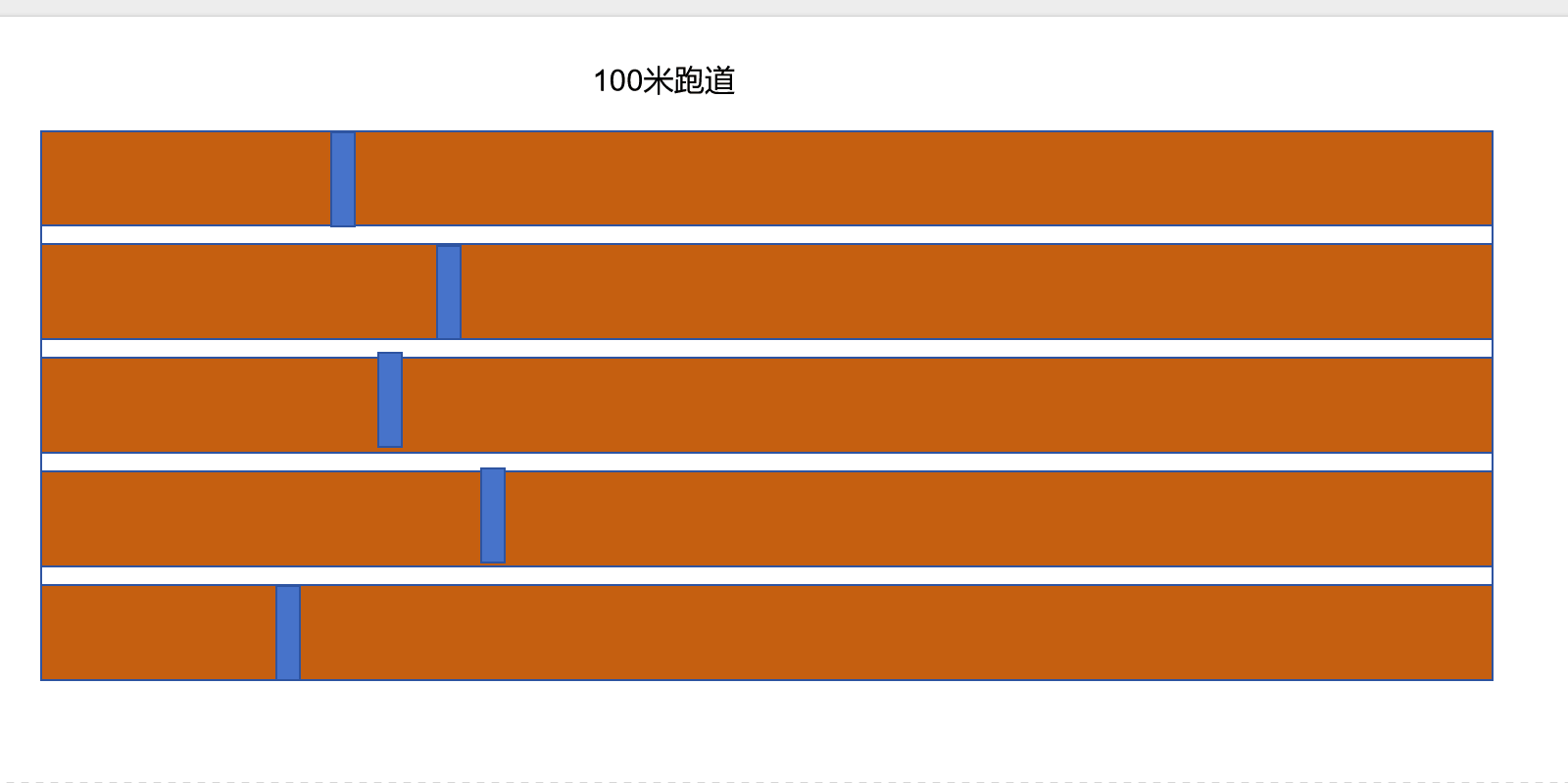
5.33 如此轉換過後,這個同一的方塊就成為了一個純粹的佔位符,就成為了一個純粹的標示而已。它僅僅只是標示著一個在位移的東西而已。跑步比賽的過程,就僅僅只是這個方塊的位移過程,這個方塊的位移過程,也就是跑步比賽的文本。
5.34 這個時候,把方塊的整個位移過程,即從起跑點位置移動到終點線位置,把這個作為時間過程的位移過程本身,以空間並列共存的形式,整個過程的每一部分,都共時地呈現出來。那麼,整個跑步比賽文本,就是一個100米跑道不同位置上的方塊,共同構成的一個序列。而由於這個方塊只是一個純粹的佔位符,自身不具有任何實質性。因此在這個過程序列中,真正實質的東西,是其所處的跑道位置。進而,這個過程的序列,實質上就是一個位置序列。實質上是跑道上每一個不同的位置,才真正意義上構成了這個作為一個序列的位移過程。
5.35 每一個位置,共同組合起來,就構成了整個100米的跑道。因此,這個位置是屬於跑道的不同位置,是跑道的組成部分。如此一來,通過懸置轉換,就會發現,在賽跑比賽這個符號表意活動中,對於運動員來說,最重要的東西是腳下所處的跑道位置,而不是自身跑步運動的視覺自然形式。每一個賽跑選手都要跑完整個跑道,因此,一個賽跑運動員進行跑步運動的過程,即生產比賽文本的過程,實際上就是生產一定量的位置的過程。
5.36 在這裡,已經揭示出跑步比賽的能指就是這個跑道上的位置。跑步遊戲的能指,不在於賽跑者自身上面,而在於賽跑者腳下的位置。因此,能指不在賽跑選手這裡,而在於跑道上面。那麼,同一意義單位的1米和1秒,其所對應的位置,具體是什麼能指呢?100米的跑道,是由什麼樣的位置組合而成的呢?
5.37 100米跑道,是作為一段空間距離而存在的。在遊戲規則中,這段距離被設定為100米的長度,它是由100個1米長度的距離單位,所組合構成的。也就是說,這段跑道被規則劃分為100個1米長度距離,這每一個1米長度距離,都是作為跑步遊戲的規則而存在的。而上面所說,每一個位置組合起來,構成了整個100米的跑道。如果位置作為能指,是一種量化的存在。那麼,按照這個規則的設定,其中的每一個位置,就必然對應於一個1米長度的空間距離。除此之外,在跑道中找不到任何量化的存在。
5.38 每一個具體的空間位置,都在遊戲規則中,量化為一個一米的空間距離。而在沒有被量化之前,它還不是表意的能指,是一種前表意的純粹自然存在,一個純粹的空間性視覺感知。只有當這個空間,被納入到一個跑道之中、成為跑道的一部分時,這個空間就通過計量工具,被遊戲規則設定為1米長的距離。
5.39 作為一個表意性的存在,這個空間距離,絕不是一個單純的物理性自然存在。只有當人們尋找到一個空間,將其作為短跑比賽的跑道時,這個空間,才能通過跑步遊戲規則,被設定為一個由諸多1米組合而成的跑道。沒有這個表意規則的設定,這個空間距離就不是跑道,僅僅只是一個單純的物理空間而已。
5.4 能指:距離單位
然而,問題出現了,1米不是同一的意義單位嗎?怎麼又變成了能指?同一個東西,怎麼又是能指,又是能指所表達的意義?因為在這裡,作為能指的1米,和作為意義的1米,僅僅只是擁有同一個詞語名稱而已,這同一個名稱,分別意指的是不同的東西。
5.41 作為能指的1米,是作為一個視覺性自然形式而存在,它是一個視覺感知中的空間範圍。每一個1米的能指本身,都是一個單獨的整體性空間範圍區域。它是一個完整不可再分的存在。而100米的跑道,就因為被切分成了100份這樣的單個空間範圍,才成為100米的跑道。或者說,因為100個這樣的單個空間範圍,共同組合在一起,才成為了100米跑道。
5.42 通常情況下,在跑道的設置中,我們基本上很難直觀到它,它僅僅只是以一個數字形式而存在。只有把100米跑道中的每一個1米的空間範圍,分別標示出來,我們才能直接直觀到這100個1米能指。只有這個時候,我們才會直觀感知到,100米跑道是由100個能指所組合而成的。
5.42 對於作為能指的1米,一個更容易幫助理解的例子是美式橄欖球的球場設置。美式橄欖球場 把球場縱向切分為100碼,即100個1碼空間距離組合成的球場。每一碼的空間範圍,都用白色標示了出來。在這裡,每兩條小標示線之間的空間範圍,作為一個被視覺感知到的空間區域形態,就是這個1碼能指的自然形式。每一個1碼能指,都是完全相同的同一個能指。

5.5 意義:距離範圍
而作為意義的1米,並不是這個作為空間區域的視覺性自然形式,而是這個空間區域的實質內容。每一個1米,作為空間區域,都是具有完全相同的距離和範圍的同一空間區域。因此,每一個1米空間區域,都是完全相同的能指。
5.51 而這個使得每一個1米能指都能夠完全相同的東西,就是1米能指所對應的意義內容。也就是說,每一個1米,都對應於完全相同的同一個意義內容。進而,每一個1米,才能是完全相同的空間範圍。
5.52 這個同一的意義內容,就是這個相同的空間距離範圍,它被設定一個具體的數值。通過同一個數值的測量和設定,每一個1米,作為一個空間區域範圍,就成為了一個相同的能指。這個被量化、作為特定數值而存在的距離數值,就是每一個1米能指,所對應的實質內容,即同一的意義單位。1米=光在真空中於1/299 792 458秒的時間內所經過的路線的長度。
5.53 在這裡,關鍵就在於區分這兩個東西:1米自身的空間性視覺形式,作為一個空間距離範圍的切分單位,和這個單位中所包含的實質範圍。而在日常的1米這個詞語表達中,這兩個東西往往被混在一起。
5.54 但是,這個區分是這裡的核心關鍵,如果不能區分,那麼就無法理解1米為什麼能夠同時成為能指和意義。1米,作為一個距離單位,這個單位本身,和其中所包含的實質性內容,並不是一回事,絕不能完全混為一談。
5.55 對於這一點,可以藉助其他的事物作為例子來幫助理解。1美元和1歐元,作為貨幣單位,同樣都是1元,但是其中所包含的內容,是完全不同的。再比如,1英里和1公里,同樣作為距離單位,都是1里路,但是其中所對應的實質範圍,是完全不同的。
5.56 在這裡,賽跑選手A和B所組合的1米單位能指,之所以是同一個1米單位,就是因為其對應的實質性範圍距離,是完全相同的同一個數值。如果A的1米單位,和B的1米單位,分別對應於不同的範圍數值,即分別是不同範圍的空間區域,那麼它們照樣可以擁有同一個名稱:1米。在這種情況下,雖然名稱相同,但意義內容就完全不一樣了。這在理論上是完全有可能的,而且在現實中,一個計量單位在其發展初期,其計量的範圍也往往是不統一的。因此,區分這兩者是極為關鍵和重要的事情。

5.6 能指:時間單位
同樣的,在時間單位上也是如此。要區分:1感知的一段運動變化,其作為時間單位;2這個時間單位中所包含的實質的運動變化範圍。
5.61 在1秒這個時間單位中,其能指的自然形式是一段感知體驗的運動變化過程,它是單純的運動變化本身的感知體驗。例如,我把一個東西從這裡移動到那裡,花費了1秒時間。在這裡,1秒時間單位的自然形式,是這個東西的空間位移過程本身的視覺感知,是這個位移運動本身,是對運動本身的視覺感知體驗。而不是這個在運動著的東西本身,也不是這個東西所處的空間位置本身。
5.62 而1秒時間單位,其對應的意義內容,就是這個運動變化過程的實質範圍。這個範圍被設定為:銫-133原子基態的兩個超精細能階之間躍遷時所輻射的電磁波的週期的9,192,631,770倍的時間。
5.63 正是由於每一個1秒的時間單位,都對應於這同一個時間範圍,因此每一個1秒,才能成為相同的能指。A選手跑步時所計量的1秒,和B選手跑步時所計量的1秒,才能是完全相同的時間單位能指。
六 示例:跑步比賽
6.1 條件1:不平衡程度<能指數量差距
現在,在確定了跑步遊戲的能指和意義之後,就可以以跑步比賽為例,具體地展示說明對局平衡的3個條件了。
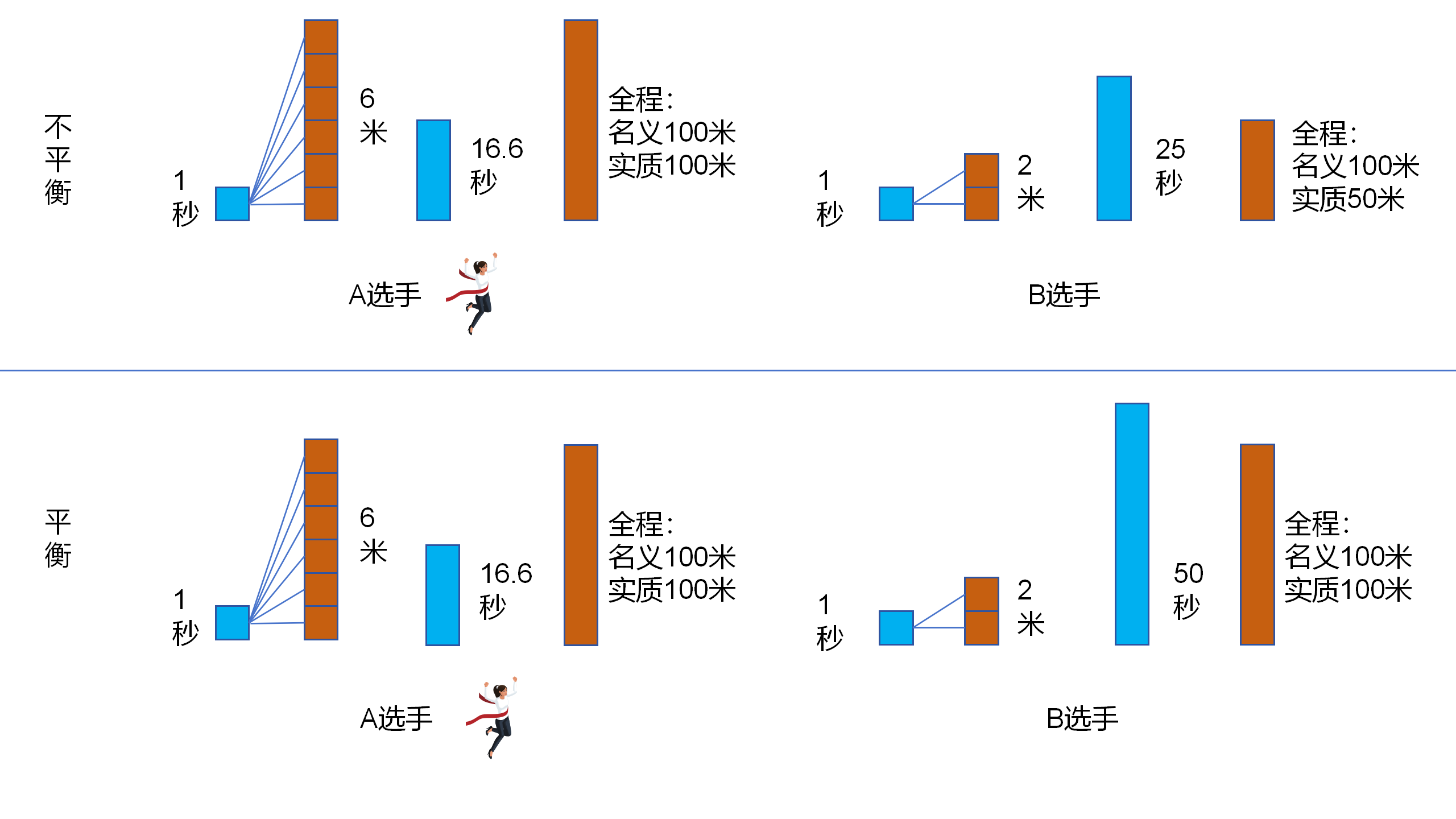
6.11 首先,要將A和B分別置於不同的符碼規則系統中。這個符碼規則就是1米和1秒,和其所對應的實質範圍。也就是說,要讓這兩者的1米和1秒,分別對應於不同的空間範圍和時間範圍。在這裡,僅僅假設一種最簡單的情況,即僅僅只是空間距離單位的不同一,時間單位是同一的。假設,B選手的1米範圍,僅僅相當於A選手的0.5米範圍,但是雙方的距離單位名稱都是1米。這樣,A的跑道全程是100米的範圍,B的跑道全程僅僅只是50米的範圍。這樣,A選手和B選手,就分別被置於不同的符碼規則系統中。這裡面的不平衡,是非常明顯的。
6.12 這時,在這種不同一的符碼規則系統下,如果A和B的速度相同,當A跑了1米的時候,B就已經跑了2米,用時相同,速度相同,兩個人跑出來的距離卻不相同。
6.13 當兩個人的速度相同,即在相同數量的時間單位內,生產出來了相同的米數,也就是生產出來了相同數量的能指。這時,兩者所跑出距離的實際範圍差距,就是這個符碼規則系統的不平衡程度。但是這個程度,並不是以一個固定的單個數字呈現出來的。因為隨著能指數量不同,這個具體的差距數值,都是不一樣的。不過,在任何一個相同數量的能指中,兩者的實際範圍,總是呈現為一個固定的比例:無論這個相同數量的能指是1、2、3......100,兩者各自生產的所有能指,所對應的總實際範圍,總是具有一個固定的比例關係。這個固定比例,正是兩者的能指單元,其對應的意義內容之間的比例:1:0.5=2:1。
6.15 因此,在這裡,跑步遊戲的不平衡程度,就是一個2:1的比例關係,即一方只是另一方的1/2。也就是說,在跑步比賽中,如果A和B的生產表現相同,即生產出了相同數量的能指,那麼A的比賽結果意義,就僅僅只是B的比賽結果意義的1/2。在此基礎上,就可以推算出,只有當A的生產表現,即能指數量,為B的2/1時,也就是2倍時,A的比賽結果意義,才能與B相同。也就是以2倍於B的速度,在相同的用時內,與B同時達到各自的終點。
6.16 進而,就可以知道,當A和B各自所生產的能指數量,彼此之間的比例關係大於2/1時,也就是一方是另一方的2倍以上時,這場不平衡規則系統下的跑步比賽,就是一場平衡的對局。因為在這種情況下,雙方生產表現差異的方向,與比賽結果意義差異的方向,是一致的。也就是說,參賽選手的生產表現,與其比賽結果意義,是相一致的。因為,在能指的意義單位同一的情況下,同樣也是這樣的結果。意義單位同一,即遊戲平衡下的比賽結果,與這個不平衡情況下的比賽結果,獲勝者和失敗者都是一樣的。也就是說,生產表現的巨大差距,抵消和cover了不平衡的負面影響。
6.18 以這個案例來說,當A的速度為B的3倍時,例如A為6m/s,B為2m/s。在遊戲不平衡的設定下,即A的全程為100米,B的全程為50米,A用時16.6秒,B用時25秒,A獲勝。在遊戲平衡的設定下,A和B的全程均為100米,A用時16.6秒,B用時50秒,依然還是A獲勝。在如此巨大的差距下,無論平衡與否,A均為獲勝者。
6.19 這個條件,是不平衡規則不利於獲勝者的情況。
6.2 條件2:意義差值方向=能指數量差距方向
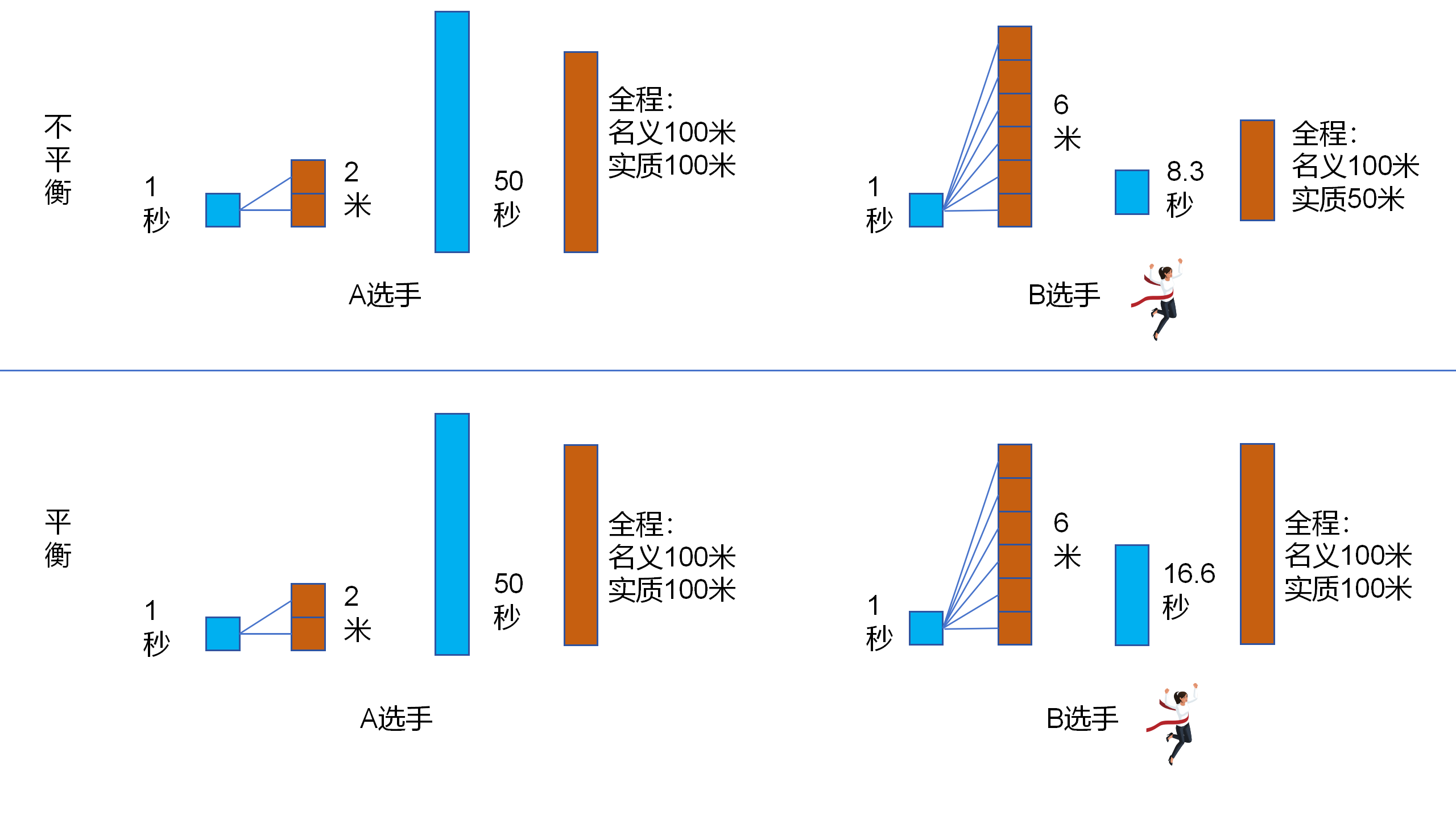
反過來,當不平衡規則利於獲勝者時,規則不平衡的方向,與勝負的方向,是一致的。規則不平衡所不利於的那一方,恰好就是生產表現更弱的那一方,也就是失敗的那一方。
6.21 設定B為獲勝者,設定B的速度為A的三倍。在遊戲不平衡的設定下,即A要跑100米,B只跑50米,B用時8.3秒,A用時50秒,B獲勝。在遊戲平衡的設定下,A和B的全程均為100米,B用時16.6秒,A用時50秒,依然還是B獲勝。在如此巨大的差距下,無論平衡與否,B均為獲勝者。
6.22 這是不平衡規則利於獲勝者的情況。
6.3條件3:失衡無法察覺
關於這一點,上面已經有更好的示例,這裡就不再闡述。
七 偶然平衡:經驗主義的設計思路
7.1
如上條件,歸結起來,無非就是一個原則:想辦法讓生產表現和比賽結果意義之間,彼此一致。這種一致,是質的一致,而不必是量的一致。也就是說,在勝負的大方向上彼此一致。而在量上,有稍許不相符,是無關緊要的事情。
7.11 也就是說,讓雙方所生產出來的能指數量之間的差距,與雙方比賽結果意義之間的差異,在方向上是一致相同的。
7.12 如果A的能指數量更多,按道理,A就應該獲勝。那麼只要每一個能指所對應的意義,共同綜合構成的意義總體,即比賽結果意義,仍然是A最好。這樣的話,哪怕規則是不平衡的,這種不平衡也不會替代參賽者,改變、決定比賽結果;這種不平衡,也似乎不會影響干擾到,比賽結果的相同不同,是由參賽者生產表現的相同不同所決定的。
7.2
當然,這裡說實際對局是平衡的對局,只是從最終的實際效果來說的。可以說,這是一種經驗主義的觀點。而在嚴格意義上,從原則上來說,它自身內在的規則系統,仍然是不平衡的。這場對局,在內在結構上仍然是不平衡的對局。它的比賽結果沒有受到不平衡規則的干擾影響,僅僅只是一種偶然。之所以偶然,是因為這種平衡,是由選手之間的表現差距所導致的,而不是規則自身所導致的必然平衡。
7.21 這場對局是平衡的,不代表下一場對局就一定會是平衡的。不平衡的規則系統,宛如達摩克利斯之劍,始終威脅著競技活動的運行。
7.22 從某種意義上來說,正是這種經驗主義的偶然平衡,大大緩衝了規則系統不平衡所帶來的嚴重破壞和干擾。從而,為遊戲設計的不平衡提供了辯護。進而,也提供了所謂相對平衡論的源泉和溫床。

最後,如果你也是對競技遊戲領域有興趣的人,那就讓我們彼此連接,共同推進這項事業的前進。感謝支持!
[未認證]競技研究社正在創作競技遊戲的理論學術研究 | 愛發電 (afdian.net)