最近看到一個求期望價格的題目,第一眼看上去覺得不過是尋常的馬爾科夫問題,但是讀罷之後發現設計者加入了一點創意,使得購買過程不再構成馬爾科夫鏈。那麼就需要尋求其他方法,可是卻得出了意料之外的結果,用AI驗證後一時也未得其因,後突然頓悟,甚覺有趣,在此作一分享
一、黑市買馬問題
在官方市場,有一匹馬的價格是500銅幣。玩家也可以前往黑市,黑市每次的入門費是20銅幣。每次進入黑市,都可能發生以下事件: (1)有1%的概率,以50銅幣購買一匹馬。 (2)有3%的概率,以100銅幣購買一匹馬。 (3)有X%的概率,以250銅幣購買一匹馬。 (4)有Y%的概率,獲得一枚碎片, 攢齊50枚碎片可以換一匹馬。 (5)有50%的概率,啥也沒有獲得。 假設市場信息暢通無阻,玩家知道這些信息。 問:如果希望黑市馬的期望價格與官方馬的價格相同,那麼事件(3)的發生概率X%應該是多少?
初看上去這似乎是一個馬爾可夫過程,下一次進入市場的狀態僅與當前有關,而與之前無關,那麼我們便可以直接列出期望價格方程進行求解,但這時便會發現情況(4)似乎打破了循環,玩家在黑市買馬時揹包裡如果已經擁有49枚碎片,便會干擾到下一次買馬的狀態,所以我們只能另尋解法。屏幕前的各位也可以先自己思考一下如何求解,看看求得的結果是否會出乎你的意料。
在遊戲的經濟系統建設中,加入黑市元素無疑會讓遊戲市場更加多元有趣,因為有現實原型的存在,玩家也很容易理解這個機制的特點,即小概率的超高收益與大概率的負收益。但受賭徒心理的影響,很多玩家都會或多或少的抱著搏一搏的心態在遊戲中嘗試一下,萬一自己歐皇附體呢?這樣就會節省一大筆錢,心情也能愉悅一整天。事實上受定勢思維影響,我們會打心底的認為黑市這種東西充滿了欺詐與騙術,看似會有高收益但是一定會有一雙無形大手在背後操盤,讓玩家輸的傾家蕩產,現實生活中確實如此。
二、題目分析
以此題為例,不考慮入場費,我們僅有1%和3%的概率分別按原價的一折與兩折買到馬(血賺!),此外還有X%的概率以五折的價格買到(小賺)。但機遇常常伴隨著風險,我們有Y%的概率只能得到一枚碎片,要想用碎片換馬我們至少要再來49次,即至少也要花費20*50=1000銅幣才能換得這匹馬(血虧),可更過分的是竟然有50%即一半的概率我們什麼也得不到,白花20銅幣(心疼)。
遊戲裡玩家看到這種設計,估計已經開始大罵官方吃相難看,裝一下都不裝,直接開始明搶了!但同時在論壇裡不斷看到有人發自己苟託到低價馬的截圖,甚至自己的好朋友也出貨了,便猶如百爪撓心,又躍躍欲試了。結果便可能是前期拿了一堆碎片,再花錢就虧本,不花錢繼續就前功盡棄,只得繼續投入。如果遊戲官方想借機回收玩家手裡的貨幣,便很可能會把玩家揹包裡的碎片持有量加入到概率公式,以在玩家獲得一定數量的碎片後減少碎片獲取概率,增大無事發生概率便能狠狠的收割這些可憐的玩家,而悲劇的是很少有人在投入大量沉沒成本後,還能保持理智及時收手,只得讓虧損最大化後悔不當初。

筆者在三國殺OL祈願臺最歐的一次,0.08%的概率直接苟託,但是後續祈願臺就被坑慘了
三、題目求解
分析了這麼多,我們還是來實際算一下,看能否通過調整X%和Y%使得馬的期望價格在數據上達到相同。既然不能直接算出期望公式,我們便先計算一下玩家平均每進入一次黑市要花費多少錢並記為
S,公式如下:
S=20+0.01×50+0.03×100+250X=23.5+250X
接著再計算玩家平均每進入一次黑市能買到幾匹馬記為N,假設我們試驗足夠多的次數,那麼根據大數定理,對於情況四就相當於我們有Y%的概率買到1/50匹馬,公式如下:
N=0.01×1+0.03×1+X+0.02Y+0.5×0=0.04+X+0.02Y
為達目的我們期望平均價格S是平均數量N的500倍,即
S=500N
接下來結合X+Y=0.46,聯立方程解得X≈-0.46%。這是一個糟糕的結果,正常情況下是不會出現概率為負的,而經過幾次驗算我們確信不是計算的問題,那麼是我們的解法有問題還是題目本身無解呢?
四、結果驗證
筆者決定藉助AI工具來驗證,首先本題的購買過程想用代碼復現並不複雜,藉助AI給出的代碼我們遍歷X從0到46,步長為1,輸出平均購買一匹馬花費最接近實際值500的情況。出乎筆者意料,代碼運行結果平均在485元/匹左右,最優情況是X趨於0,Y趨於0.46時,這也就意味著玩家進入黑市買馬的期望價格竟然低於正常買馬價格!而按照我們的設想,黑市買馬的平均花費一定是會大於正常買馬的,這也符合我們看到題設條件的第一印象,所以這是否意味著真的存在一個X,能夠使黑市買馬與正常買馬的期望價格相等?

PyCharm運行結果展示
接著就需要AI給出一個算法思想,GPT4.0給出了一個結果同為負數的求解算法,表明題目無解,但是算法過程有明顯錯誤故未採納。與此同時,筆者的朋友動用了當下最先進的Open AI o1模型,給出了一個遞歸思想的算法,過程如下圖:

o1模型給出的算法
AI藉助其強大的算力,將本題拆分後“暴力求解”,具體如何遞歸計算出X的過程並沒有給出。出於對o1模型的信任,筆者和朋友陷入了一陣自我懷疑當中,但仍不知錯在何處,且這種遞歸算法短期內並不能求證真偽。沒想到這樣一個看似簡單的期望求解卻讓人陷入了山重水複疑無路的境地。
五、柳暗花明
轉機出現在將AI給出的結果代入到代碼當中,我們發現運行的結果仍然小於500,甚至比剛才的情況還要更小!這時筆者的朋友提出了一個想法
有沒有可能在所給條件下通過黑市買馬,無論如何都是會賺的呢?
一語道破,柳暗花明。由於定勢思維,我們早早的把結果確定在了只虧不賺上,導致忽略了只賺不虧的情形,所以在一開始模擬購買時,我們讓X正向遍歷得到的結果只有一個,即X=0,Y=0.46,這種極端情況下玩家通過黑市買馬的期望價格最接近原價。一旦我們讓X從46反向遍歷到0,我們便會得到如下結果
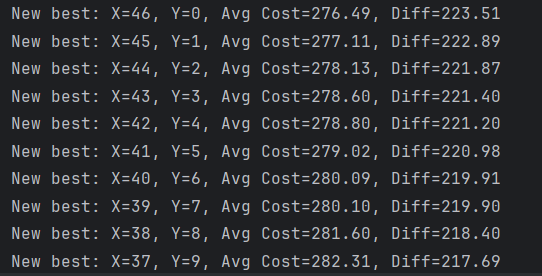
反向遍歷結果展實(部分)
所以結果證明這個黑市系統竟然是一個穩賺不賠的遊戲機制,在明晃晃的陷阱下竟包藏著官方滿滿的良心(bushi)!
六、結尾
其實現實不少遊戲中如魔獸世界、荒野大鏢客等都設有黑市系統,玩家可以在黑市中購買一些稀有道具或者出售自己多餘的物品,而在黑市中的物品價格往往都帶有隨機性,同一物品的價格在兩次進入黑市後可能天差地別。如果官方有公佈黑市規則的話,玩家可以自行研究一下是否值得,但如果規則對外隱藏的話,筆者建議還是儘量不要嘗試這類帶有賭博性質的活動,因為大部分情況下官方都不希望玩家能夠從一個新機制中獲利,最常見的情況是期望價格與正常價格相等,像本題這種低於正常價格的情形大概率是遊戲策劃自己計算失誤了hah。
最後,感謝各位看完本文,題目本身不難甚至是道錯題,但是解題過程中卻帶給筆者不少思考,有時思維定勢真的可能會影響我們做出決策,而且我們所看到的數值有時也會欺騙我們的直覺,此時就需要親自動手驗算一下了。如果屏幕前的你有其他的一些想法,也歡迎在評論區討論,我們下期再見!
