最近看到一个求期望价格的题目,第一眼看上去觉得不过是寻常的马尔科夫问题,但是读罢之后发现设计者加入了一点创意,使得购买过程不再构成马尔科夫链。那么就需要寻求其他方法,可是却得出了意料之外的结果,用AI验证后一时也未得其因,后突然顿悟,甚觉有趣,在此作一分享
一、黑市买马问题
在官方市场,有一匹马的价格是500铜币。玩家也可以前往黑市,黑市每次的入门费是20铜币。每次进入黑市,都可能发生以下事件: (1)有1%的概率,以50铜币购买一匹马。 (2)有3%的概率,以100铜币购买一匹马。 (3)有X%的概率,以250铜币购买一匹马。 (4)有Y%的概率,获得一枚碎片, 攒齐50枚碎片可以换一匹马。 (5)有50%的概率,啥也没有获得。 假设市场信息畅通无阻,玩家知道这些信息。 问:如果希望黑市马的期望价格与官方马的价格相同,那么事件(3)的发生概率X%应该是多少?
初看上去这似乎是一个马尔可夫过程,下一次进入市场的状态仅与当前有关,而与之前无关,那么我们便可以直接列出期望价格方程进行求解,但这时便会发现情况(4)似乎打破了循环,玩家在黑市买马时背包里如果已经拥有49枚碎片,便会干扰到下一次买马的状态,所以我们只能另寻解法。屏幕前的各位也可以先自己思考一下如何求解,看看求得的结果是否会出乎你的意料。
在游戏的经济系统建设中,加入黑市元素无疑会让游戏市场更加多元有趣,因为有现实原型的存在,玩家也很容易理解这个机制的特点,即小概率的超高收益与大概率的负收益。但受赌徒心理的影响,很多玩家都会或多或少的抱着搏一搏的心态在游戏中尝试一下,万一自己欧皇附体呢?这样就会节省一大笔钱,心情也能愉悦一整天。事实上受定势思维影响,我们会打心底的认为黑市这种东西充满了欺诈与骗术,看似会有高收益但是一定会有一双无形大手在背后操盘,让玩家输的倾家荡产,现实生活中确实如此。
二、题目分析
以此题为例,不考虑入场费,我们仅有1%和3%的概率分别按原价的一折与两折买到马(血赚!),此外还有X%的概率以五折的价格买到(小赚)。但机遇常常伴随着风险,我们有Y%的概率只能得到一枚碎片,要想用碎片换马我们至少要再来49次,即至少也要花费20*50=1000铜币才能换得这匹马(血亏),可更过分的是竟然有50%即一半的概率我们什么也得不到,白花20铜币(心疼)。
游戏里玩家看到这种设计,估计已经开始大骂官方吃相难看,装一下都不装,直接开始明抢了!但同时在论坛里不断看到有人发自己苟托到低价马的截图,甚至自己的好朋友也出货了,便犹如百爪挠心,又跃跃欲试了。结果便可能是前期拿了一堆碎片,再花钱就亏本,不花钱继续就前功尽弃,只得继续投入。如果游戏官方想借机回收玩家手里的货币,便很可能会把玩家背包里的碎片持有量加入到概率公式,以在玩家获得一定数量的碎片后减少碎片获取概率,增大无事发生概率便能狠狠的收割这些可怜的玩家,而悲剧的是很少有人在投入大量沉没成本后,还能保持理智及时收手,只得让亏损最大化后悔不当初。

笔者在三国杀OL祈愿台最欧的一次,0.08%的概率直接苟托,但是后续祈愿台就被坑惨了
三、题目求解
分析了这么多,我们还是来实际算一下,看能否通过调整X%和Y%使得马的期望价格在数据上达到相同。既然不能直接算出期望公式,我们便先计算一下玩家平均每进入一次黑市要花费多少钱并记为
S,公式如下:
S=20+0.01×50+0.03×100+250X=23.5+250X
接着再计算玩家平均每进入一次黑市能买到几匹马记为N,假设我们试验足够多的次数,那么根据大数定理,对于情况四就相当于我们有Y%的概率买到1/50匹马,公式如下:
N=0.01×1+0.03×1+X+0.02Y+0.5×0=0.04+X+0.02Y
为达目的我们期望平均价格S是平均数量N的500倍,即
S=500N
接下来结合X+Y=0.46,联立方程解得X≈-0.46%。这是一个糟糕的结果,正常情况下是不会出现概率为负的,而经过几次验算我们确信不是计算的问题,那么是我们的解法有问题还是题目本身无解呢?
四、结果验证
笔者决定借助AI工具来验证,首先本题的购买过程想用代码复现并不复杂,借助AI给出的代码我们遍历X从0到46,步长为1,输出平均购买一匹马花费最接近实际值500的情况。出乎笔者意料,代码运行结果平均在485元/匹左右,最优情况是X趋于0,Y趋于0.46时,这也就意味着玩家进入黑市买马的期望价格竟然低于正常买马价格!而按照我们的设想,黑市买马的平均花费一定是会大于正常买马的,这也符合我们看到题设条件的第一印象,所以这是否意味着真的存在一个X,能够使黑市买马与正常买马的期望价格相等?

PyCharm运行结果展示
接着就需要AI给出一个算法思想,GPT4.0给出了一个结果同为负数的求解算法,表明题目无解,但是算法过程有明显错误故未采纳。与此同时,笔者的朋友动用了当下最先进的Open AI o1模型,给出了一个递归思想的算法,过程如下图:

o1模型给出的算法
AI借助其强大的算力,将本题拆分后“暴力求解”,具体如何递归计算出X的过程并没有给出。出于对o1模型的信任,笔者和朋友陷入了一阵自我怀疑当中,但仍不知错在何处,且这种递归算法短期内并不能求证真伪。没想到这样一个看似简单的期望求解却让人陷入了山重水复疑无路的境地。
五、柳暗花明
转机出现在将AI给出的结果代入到代码当中,我们发现运行的结果仍然小于500,甚至比刚才的情况还要更小!这时笔者的朋友提出了一个想法
有没有可能在所给条件下通过黑市买马,无论如何都是会赚的呢?
一语道破,柳暗花明。由于定势思维,我们早早的把结果确定在了只亏不赚上,导致忽略了只赚不亏的情形,所以在一开始模拟购买时,我们让X正向遍历得到的结果只有一个,即X=0,Y=0.46,这种极端情况下玩家通过黑市买马的期望价格最接近原价。一旦我们让X从46反向遍历到0,我们便会得到如下结果
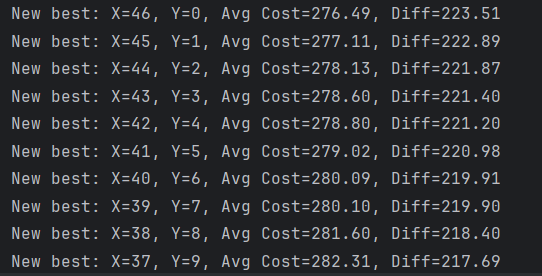
反向遍历结果展实(部分)
所以结果证明这个黑市系统竟然是一个稳赚不赔的游戏机制,在明晃晃的陷阱下竟包藏着官方满满的良心(bushi)!
六、结尾
其实现实不少游戏中如魔兽世界、荒野大镖客等都设有黑市系统,玩家可以在黑市中购买一些稀有道具或者出售自己多余的物品,而在黑市中的物品价格往往都带有随机性,同一物品的价格在两次进入黑市后可能天差地别。如果官方有公布黑市规则的话,玩家可以自行研究一下是否值得,但如果规则对外隐藏的话,笔者建议还是尽量不要尝试这类带有赌博性质的活动,因为大部分情况下官方都不希望玩家能够从一个新机制中获利,最常见的情况是期望价格与正常价格相等,像本题这种低于正常价格的情形大概率是游戏策划自己计算失误了hah。
最后,感谢各位看完本文,题目本身不难甚至是道错题,但是解题过程中却带给笔者不少思考,有时思维定势真的可能会影响我们做出决策,而且我们所看到的数值有时也会欺骗我们的直觉,此时就需要亲自动手验算一下了。如果屏幕前的你有其他的一些想法,也欢迎在评论区讨论,我们下期再见!
