1. 寻找游戏平衡
避免”一条狭窄的获胜策略“&”某个系统拥有不可逾越的优势“,平衡为玩家的自由探索提供了空间,用于玩家验证自己的心智模型。即,玩家无法迅速掌握获胜的诀窍,同时为所有玩家提供公平的机会。
从玩家角度,平衡代表着”游戏中所有玩家都承担着风险,即使失败也能恢复到以前的状态“
平衡是动态的,并通过迭代设计与测试来实现。
2. 方法与工具概述
定性和定量方法并非单一,而是可以互补的。
基于设计师的平衡:
平衡游戏的第一个主要方法是设计师的定性直觉,不同的设计师对平衡会有不同的理解。但仅通过定性直觉的平衡设计会犯下可怕的错误。启发式的平衡设计存在自身的极限,同时基于个人的设计会导致分歧和冲突的出现。
基于玩家的平衡:
玩家与游戏交互,设计师与该交互的结果进行交互,以对游戏进行改动。该步骤是游戏测试的核心内容。游戏测试极其有价值,是游戏设计师工具集的一部分。
分析法:
对数据进行分析不可避免地有一定程度的主观诠释,但该方法依然属于定量的方法。通过分析清除大量备选项,,并用对应的数据填充。常见的整体统计数据诸如留存,下载量,付费率等,较小的统计数据例如关卡的平均通关时间,特定任务的完成率等。通过数据分析找到最重要的相关性,并调整游戏平衡。通过玩家推进游戏的方式来评估游戏平衡。
需要注意的是,即使拥有足够的数据,分析法并不能发现所有游戏中存在的问题。仅通过收集数据,将其整合为一款游戏的并不会取得成功。数据需要在具体环境中进行诠释,并不能凌驾一切。
同时,样本量较小和信息失真也是在测试阶段容易产生的问题,特定的玩家群体和社区有时并不能做出有效代表。
数学方法:
通过数学建模进行平衡设计不像分析法是后顾性的,而是以前瞻性的视角构建游戏将如何运作的模型。
一般来说,数学建模技术是帮助确保以下内容:
(1)不同对象的成本和收益是平衡的
(2)不存在能击败所有个体或被所有个体击败的对象
(3)游戏中目标进程,成本进程和奖励进程以大致相同的速度推进,且该速度符合玩家公平和参与感。
3. 在游戏平衡中使用概率
概率作为定量工具在游戏平衡中担任重要角色。在具体的游戏中,设计师使用概率模拟并未真正实现的系统。
游戏设计师必须清楚游戏系统层次结构中的最低点位置,其表现为具体的名称与对应的数值,而非构成子系统。而概率提供过于难解和精细系统和合理替代数值。例如用命中率代替具体的刀剑和怪物的物理交互结果。
随机结果由代码生成的随机数控制,这种随机过程是简单的,只要代码所产生的随机数的周期低于可辩别的水平,对大部分游戏来说就是可接受的。且在大多数情况下,重要的是功能上可接受的随机性。
独立事件和相关事件:
以掷硬币为例,当将每次掷硬币当作独立事件看待,正反两面的概率都为50%,上一次的投掷结果并不会影响下一次的结果。
而当一组事件影响共同结果时,例如三次投掷硬币都是正面朝上,该事件就变得开始互相关联。最终结果的概率为每次结果概率的乘积(上述例子的概率为0.5*0.5*0.5=0.125)
概率分布:
在投掷两个D6骰子并将点数之和作为结果时,并非2-12的每个数字出现的概率都相同。计算方法是产生不同组合的数量除以骰子的面数(6),并自乘骰子数量的次数。
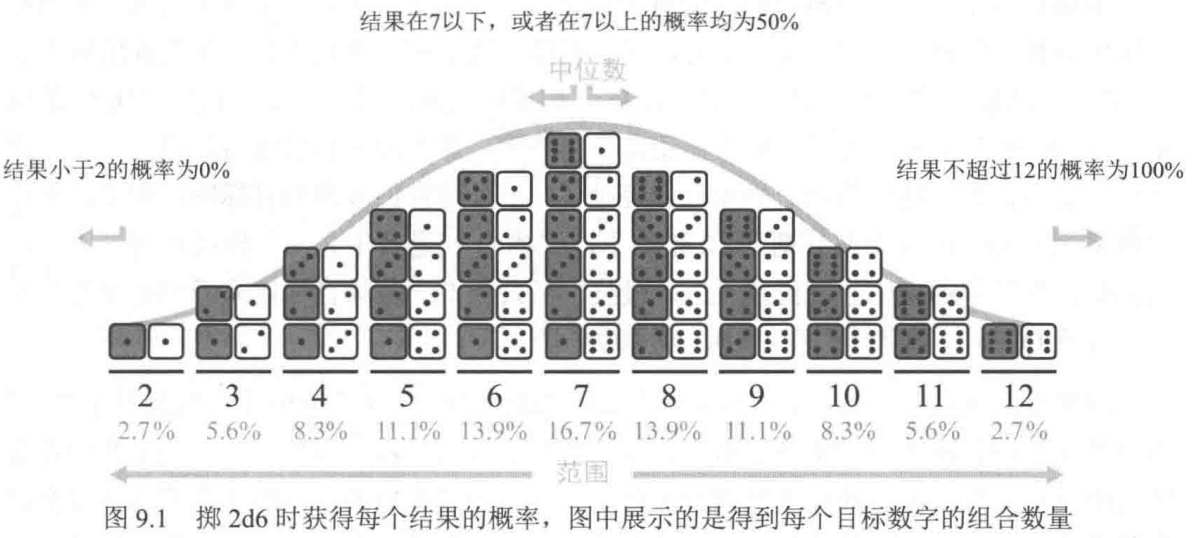
如上图所示,概率曲线组成了中间高两侧低的曲线形状,该分布被称为正态分布或高斯分布。当具有独立概率的多个事件一起相互作用时,通常出现该分布的特征。
在该分布中,均值为所有可能出现结果的平均数,曲线的顶部作为众数代表概率最高的结果。另,处于分布中央的的数字,即高于它和低于它的数字相等的特殊数字为中位数。分布所横跨的值为范围。
在对称分布中,均值,众数,中位数是相等的。但在游戏设计中,许多角色的属性分布并非对称分布,而且由明显的分布偏移。例如在1-100的范围内,某个角色造成的伤害均值可能高于50,则代表该角色相较于平均的,无优势的角色更强。
变化的概率:
例如在一副扑克牌中寻找特定的牌,每次抽取时不放回,则抽到该牌的概率一直处在变化中。
这种概率变化多用于赋予玩家“正在接近目标”的实际感觉(目标本身仅基于概率,而非玩家精通程度)。大量游戏中存在的盲盒玩法,会为不断抽奖的玩家积累中奖概率,以保持玩家的参与感。
认知偏差和三门问题:
一般来说,玩家不善于理解和估计概率。所谓的“三门问题”,一扇空的门,一扇有奖品的门和一扇背后有脏兮兮山羊的门。在玩家选择一扇门后,直到哪扇门存在奖品的主持人打开了另一扇门,玩家看到山羊后可以更换自己的选择。
从一般视角来看,玩家是否更换选择并未影响得奖的概率,但事实上换门是有利的,从数学上玩家的得奖概率在换门前是1/3,和换门后则是2/3。
该问题的核心是概率和人民的认知偏差有关。在本问题中,有一个要素是主持人知道门代表的答案,他并没有随机选择门,而是打开了有着山羊的门。
当玩家第一次选择是,获奖概率是1/3,而失败的几率则是2/3.而当知道答案的主持人选择山羊门时,他并没有随机打开三门中的一个,而是认为选择了山羊门。这意味着对你来说,中奖的概率仍然是1/3,但另一扇门拥有剩下的全部可能,即2/3的中奖率。
理解概率依据我们对其作用原理的认知偏差,是游戏设计师的重要技能。
公平:
玩家对于概率的认知主要包括“是否公平”是否平衡“。若玩家投掷六面骰子多次都为结果1,则会认为该游戏是不公平的。玩家会认为数学期望所代表的概率是正确的,即1/3的概率中奖,那么第三次一定中奖的感觉。玩家会以直觉行事,游戏的设计目的也是为例玩家的参与感和愉悦度,并非统计上的严谨性。
极低概率事件仍有发生的可能:
在玩家众多时,即使概率极低的事件也有可能会独立发生,因为玩家投掷骰子的次数足够多。当你希望极低概率的事件出现时,,也可尝试倾斜比例或依赖庞大的玩家基数来使其发生。例如”差一点中“的概率误读,例如玩家需要凑齐四件相同物体获得升级,先让玩家获得其中的三个,在第四次提供离该物品很相近的道具。这一切可以在软件中预先设计好,但会使得玩家有”下一次就会中“的错误体验。
4. 传递系统与非传递系统
传递平衡:
在具有传递部分所组成的系统中,每个部分都会优于一个特定部分,同时劣于另一个部分,例如石头剪刀布。类似具有传递关系的系统也包括金木水火土相生相克。
传递平衡的必要条件:
为了传递性的平衡一个系统,该系统必须包含奇数个部分,且满足“刚好能胜过剩余系统的一半,同时被另一半胜过”。同时,这种部分之间的控制有可能是概率性的,可知关系并不一定能带来确定性的胜利,但必须具有清晰明了的优势。偶数系统并不能维持稳定的传递平衡,例如魔兽中的部落和联盟,总会出现不均等的劣势或者优势。
实现传递平衡:
创建动态平衡的传递式游戏系统,通常在系统中各个部分共享的多个属性上下功夫。例如给步兵,骑兵,弓箭手配置四种属性:攻击、防御、射程、速度

如上图,每个兵种拥有相同的总体点数。同时在游戏中存在明显的克制关系:
步兵通过高攻击和足够的防御克制骑兵
骑兵通过高速度和足够的攻击克制弓兵
弓兵通过高射程和足够的速度克制步兵
不论如何,战斗系统是作为更大系统的一部分存在,这突出了游戏测试如此重要的原因:系统不能太严格使得对外部无反应。例如玩家使用弓箭手卡在岩石后面变得无敌,就使得弓箭手成为唯一制胜策略。故需要考虑其它系统对传递系统设计上的干扰。
非传递平衡:
当上述内容单独来看时,即仅包含步兵和骑兵两种兵种时,出现了非传递平衡的例子,即对任意两种不同的部分,其中一种优于另一种。本质上不平衡的传递通常会基于其成本和收益来进行平衡,例如风险代表更高的收益或者更低的成本。
非传递平衡系统会出现在包含进步系统的大部分游戏中,它通常的玩法体验包括玩家获得的某种形式的进步。例如玩家控制的军队,资源等内容在效用方面有所提升时。
使用这种方法解释游戏中对象会使得玩家更容易理解:生锈的匕首一般会比崭新的巨剑要便宜。而如何参考两者之间的属性差距进而确定成本差距也是设计师需要考虑的问题。通常需要保证这种差距是成比例的,并需要大量迭代来保持平衡。平衡非传递系统,需要定义必要的进程曲线。