1. 尋找遊戲平衡
避免”一條狹窄的獲勝策略“&”某個系統擁有不可逾越的優勢“,平衡為玩家的自由探索提供了空間,用於玩家驗證自己的心智模型。即,玩家無法迅速掌握獲勝的訣竅,同時為所有玩家提供公平的機會。
從玩家角度,平衡代表著”遊戲中所有玩家都承擔著風險,即使失敗也能恢復到以前的狀態“
平衡是動態的,並通過迭代設計與測試來實現。
2. 方法與工具概述
定性和定量方法並非單一,而是可以互補的。
基於設計師的平衡:
平衡遊戲的第一個主要方法是設計師的定性直覺,不同的設計師對平衡會有不同的理解。但僅通過定性直覺的平衡設計會犯下可怕的錯誤。啟發式的平衡設計存在自身的極限,同時基於個人的設計會導致分歧和衝突的出現。
基於玩家的平衡:
玩家與遊戲交互,設計師與該交互的結果進行交互,以對遊戲進行改動。該步驟是遊戲測試的核心內容。遊戲測試極其有價值,是遊戲設計師工具集的一部分。
分析法:
對數據進行分析不可避免地有一定程度的主觀詮釋,但該方法依然屬於定量的方法。通過分析清除大量備選項,,並用對應的數據填充。常見的整體統計數據諸如留存,下載量,付費率等,較小的統計數據例如關卡的平均通關時間,特定任務的完成率等。通過數據分析找到最重要的相關性,並調整遊戲平衡。通過玩家推進遊戲的方式來評估遊戲平衡。
需要注意的是,即使擁有足夠的數據,分析法並不能發現所有遊戲中存在的問題。僅通過收集數據,將其整合為一款遊戲的並不會取得成功。數據需要在具體環境中進行詮釋,並不能凌駕一切。
同時,樣本量較小和信息失真也是在測試階段容易產生的問題,特定的玩家群體和社區有時並不能做出有效代表。
數學方法:
通過數學建模進行平衡設計不像分析法是後顧性的,而是以前瞻性的視角構建遊戲將如何運作的模型。
一般來說,數學建模技術是幫助確保以下內容:
(1)不同對象的成本和收益是平衡的
(2)不存在能擊敗所有個體或被所有個體擊敗的對象
(3)遊戲中目標進程,成本進程和獎勵進程以大致相同的速度推進,且該速度符合玩家公平和參與感。
3. 在遊戲平衡中使用概率
概率作為定量工具在遊戲平衡中擔任重要角色。在具體的遊戲中,設計師使用概率模擬並未真正實現的系統。
遊戲設計師必須清楚遊戲系統層次結構中的最低點位置,其表現為具體的名稱與對應的數值,而非構成子系統。而概率提供過於難解和精細系統和合理替代數值。例如用命中率代替具體的刀劍和怪物的物理交互結果。
隨機結果由代碼生成的隨機數控制,這種隨機過程是簡單的,只要代碼所產生的隨機數的週期低於可辯別的水平,對大部分遊戲來說就是可接受的。且在大多數情況下,重要的是功能上可接受的隨機性。
獨立事件和相關事件:
以擲硬幣為例,當將每次擲硬幣當作獨立事件看待,正反兩面的概率都為50%,上一次的投擲結果並不會影響下一次的結果。
而當一組事件影響共同結果時,例如三次投擲硬幣都是正面朝上,該事件就變得開始互相關聯。最終結果的概率為每次結果概率的乘積(上述例子的概率為0.5*0.5*0.5=0.125)
概率分佈:
在投擲兩個D6骰子並將點數之和作為結果時,並非2-12的每個數字出現的概率都相同。計算方法是產生不同組合的數量除以骰子的面數(6),並自乘骰子數量的次數。
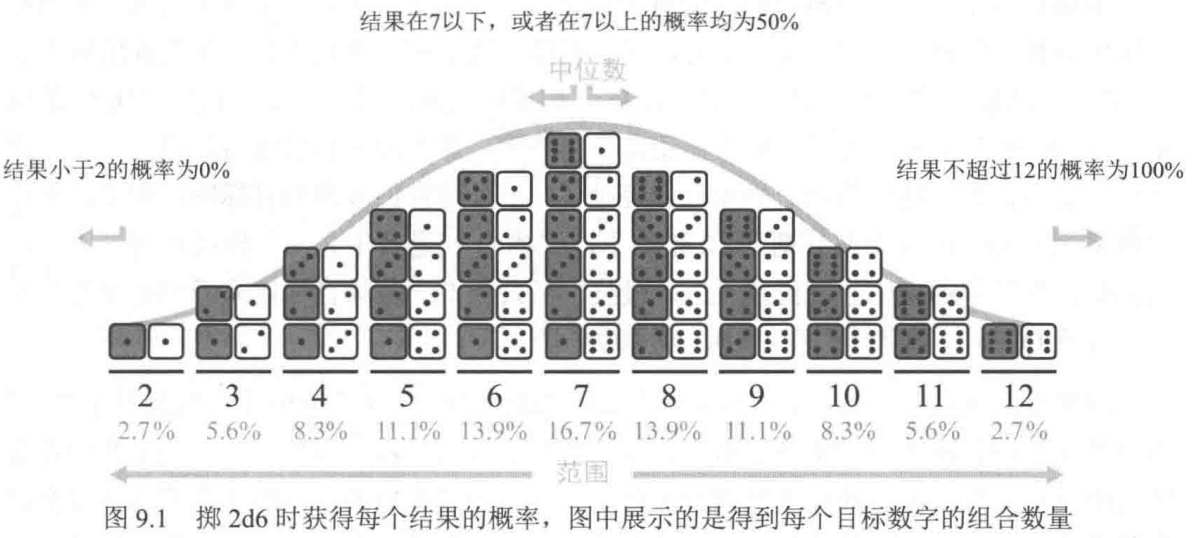
如上圖所示,概率曲線組成了中間高兩側低的曲線形狀,該分佈被稱為正態分佈或高斯分佈。當具有獨立概率的多個事件一起相互作用時,通常出現該分佈的特徵。
在該分佈中,均值為所有可能出現結果的平均數,曲線的頂部作為眾數代表概率最高的結果。另,處於分佈中央的的數字,即高於它和低於它的數字相等的特殊數字為中位數。分佈所橫跨的值為範圍。
在對稱分佈中,均值,眾數,中位數是相等的。但在遊戲設計中,許多角色的屬性分佈並非對稱分佈,而且由明顯的分佈偏移。例如在1-100的範圍內,某個角色造成的傷害均值可能高於50,則代表該角色相較於平均的,無優勢的角色更強。
變化的概率:
例如在一副撲克牌中尋找特定的牌,每次抽取時不放回,則抽到該牌的概率一直處在變化中。
這種概率變化多用於賦予玩家“正在接近目標”的實際感覺(目標本身僅基於概率,而非玩家精通程度)。大量遊戲中存在的盲盒玩法,會為不斷抽獎的玩家積累中獎概率,以保持玩家的參與感。
認知偏差和三門問題:
一般來說,玩家不善於理解和估計概率。所謂的“三門問題”,一扇空的門,一扇有獎品的門和一扇背後有髒兮兮山羊的門。在玩家選擇一扇門後,直到哪扇門存在獎品的主持人打開了另一扇門,玩家看到山羊後可以更換自己的選擇。
從一般視角來看,玩家是否更換選擇並未影響得獎的概率,但事實上換門是有利的,從數學上玩家的得獎概率在換門前是1/3,和換門後則是2/3。
該問題的核心是概率和人民的認知偏差有關。在本問題中,有一個要素是主持人知道門代表的答案,他並沒有隨機選擇門,而是打開了有著山羊的門。
當玩家第一次選擇是,獲獎概率是1/3,而失敗的幾率則是2/3.而當知道答案的主持人選擇山羊門時,他並沒有隨機打開三門中的一個,而是認為選擇了山羊門。這意味著對你來說,中獎的概率仍然是1/3,但另一扇門擁有剩下的全部可能,即2/3的中獎率。
理解概率依據我們對其作用原理的認知偏差,是遊戲設計師的重要技能。
公平:
玩家對於概率的認知主要包括“是否公平”是否平衡“。若玩家投擲六面骰子多次都為結果1,則會認為該遊戲是不公平的。玩家會認為數學期望所代表的概率是正確的,即1/3的概率中獎,那麼第三次一定中獎的感覺。玩家會以直覺行事,遊戲的設計目的也是為例玩家的參與感和愉悅度,並非統計上的嚴謹性。
極低概率事件仍有發生的可能:
在玩家眾多時,即使概率極低的事件也有可能會獨立發生,因為玩家投擲骰子的次數足夠多。當你希望極低概率的事件出現時,,也可嘗試傾斜比例或依賴龐大的玩家基數來使其發生。例如”差一點中“的概率誤讀,例如玩家需要湊齊四件相同物體獲得升級,先讓玩家獲得其中的三個,在第四次提供離該物品很相近的道具。這一切可以在軟件中預先設計好,但會使得玩家有”下一次就會中“的錯誤體驗。
4. 傳遞系統與非傳遞系統
傳遞平衡:
在具有傳遞部分所組成的系統中,每個部分都會優於一個特定部分,同時劣於另一個部分,例如石頭剪刀布。類似具有傳遞關係的系統也包括金木水火土相生相剋。
傳遞平衡的必要條件:
為了傳遞性的平衡一個系統,該系統必須包含奇數個部分,且滿足“剛好能勝過剩餘系統的一半,同時被另一半勝過”。同時,這種部分之間的控制有可能是概率性的,可知關係並不一定能帶來確定性的勝利,但必須具有清晰明瞭的優勢。偶數系統並不能維持穩定的傳遞平衡,例如魔獸中的部落和聯盟,總會出現不均等的劣勢或者優勢。
實現傳遞平衡:
創建動態平衡的傳遞式遊戲系統,通常在系統中各個部分共享的多個屬性上下功夫。例如給步兵,騎兵,弓箭手配置四種屬性:攻擊、防禦、射程、速度

如上圖,每個兵種擁有相同的總體點數。同時在遊戲中存在明顯的剋制關係:
步兵通過高攻擊和足夠的防禦剋制騎兵
騎兵通過高速度和足夠的攻擊剋制弓兵
弓兵通過高射程和足夠的速度剋制步兵
不論如何,戰鬥系統是作為更大系統的一部分存在,這突出了遊戲測試如此重要的原因:系統不能太嚴格使得對外部無反應。例如玩家使用弓箭手卡在岩石後面變得無敵,就使得弓箭手成為唯一制勝策略。故需要考慮其它系統對傳遞系統設計上的干擾。
非傳遞平衡:
當上述內容單獨來看時,即僅包含步兵和騎兵兩種兵種時,出現了非傳遞平衡的例子,即對任意兩種不同的部分,其中一種優於另一種。本質上不平衡的傳遞通常會基於其成本和收益來進行平衡,例如風險代表更高的收益或者更低的成本。
非傳遞平衡系統會出現在包含進步系統的大部分遊戲中,它通常的玩法體驗包括玩家獲得的某種形式的進步。例如玩家控制的軍隊,資源等內容在效用方面有所提升時。
使用這種方法解釋遊戲中對象會使得玩家更容易理解:生鏽的匕首一般會比嶄新的巨劍要便宜。而如何參考兩者之間的屬性差距進而確定成本差距也是設計師需要考慮的問題。通常需要保證這種差距是成比例的,並需要大量迭代來保持平衡。平衡非傳遞系統,需要定義必要的進程曲線。