隨著植物大戰殭屍雜交版的爆火,我也回想起小時候和父親一起玩植物大戰殭屍的日子,記得當時我特別喜歡把向日癸種在最左側第一排,而父親卻喜歡將豌豆射手放在那兒,特別不能理解為什麼,還時常詢問老爸為什麼。

現在上了大學突然意識到這個問題可能能通過數學建模完成,於是我就嘗試了一下(不過我不是該專業方向的,有問題和想法也歡迎指正和討論)
《植物大戰殭屍》是一塔防類策略遊戲,玩家在每一關卡中種植植物抵禦各種殭屍入侵。
本文在分析植物大戰殭屍人機博弈機制的基礎上對博弈邏輯進行了模擬,通過遺傳算法、動態規劃求解植物大戰殭屍一般通關模型,得到通關最優策略及最大陽光數量,並使用隨機模擬及隱馬爾科夫神經網絡對 未知殭屍生成情況下的關卡進行模擬分析求解,
使用統計分析方法得到更復雜情況的最優策略及最大陽光數量期望。
1. 參數定義
1. 時間參數
t:時間,以秒為單位。
2. 場地參數
G:網格大小,表示遊戲場地的行和列。
Gij:表示場地上第 i 行第 j 列的格子。
3. 植物參數
P:植物集合。
Pi:第 i 種植物。
C(Pi):種植植物 Pi 所需的陽光數量。
A(Pi):植物Pi 的攻擊力。
R(Pi):植物Pi 的生產陽光速率(生產植物)。
H(Pi):植物Pi 的生命值。
4. 殭屍參數
Z:殭屍集合。
Zj:第 j 種殭屍。
S(Zjj):殭屍 Zj 的速度。
D(Zj):殭屍Zj 的耐久度(生命值)。
E(Zj):殭屍Zj 吃植物所需的時間。
5. 遊戲參數
Y:當前陽光數量。
2. 通關模型建立
1. 狀態定義
S(t):時間 t 時的遊戲狀態,包括植物位置、殭屍位置、陽光數量等。
2. 狀態轉移
植物生長:每秒生產植物增加陽光數量。
植物攻擊:攻擊植物對殭屍造成傷害,殭屍生命值減少。
殭屍移動:殭屍每秒向左移動一格。
殭屍攻擊:殭屍吃掉植物,植物生命值減少。
3. 目標函數
最大化陽光數量:max∑t=0TY(t)\max \sum_{t=0}^{T} Y(t)max∑t=0TY(t)
通關條件:在所有殭屍到達最左側前將其消滅。
4. 約束條件
植物種植:Y(t)≥C(Pi)Y(t) \geq C(P_i)Y(t)≥C(Pi)
植物生命:H(Pi,t)>0H(P_i, t) > 0H(Pi,t)>0
殭屍生命:D(Zj,t)≤0D(Z_j, t) \leq 0D(Zj,t)≤0
3. 最終模型建立
1. 遺傳算法優化
初始化:生成初始種植策略集合。
適應度函數:根據陽光數量、通關時間等評估每個策略的優劣。
選擇:選擇適應度高的策略進行交叉和變異。
迭代:多次迭代,直到找到最優策略。
2. 動態規劃求解
階段劃分:將遊戲過程分為若干階段,每個階段為一個子問題。
狀態定義:每個階段的狀態包括當前植物和殭屍的狀態、陽光數量等。
狀態轉移:根據當前狀態和決策轉移到下一狀態。
最優策略:通過動態規劃找到每個階段的最優策略,最終獲得全局最優解。
3. 隨機模擬
模擬過程:通過大量隨機模擬評估不同策略的效果。
結果分析:統計分析不同策略在各種情況下的表現,找出最優策略和最大陽光數量期望。
4. 隱馬爾科夫模型和神經網絡預測
殭屍生成預測:結合隱馬爾科夫模型和神經網絡預測殭屍的生成模式。
策略調整:根據預測結果動態調整策略,提高通關成功率。
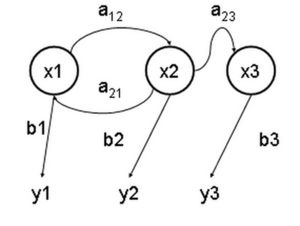
通過對上述模型的分析,可以判斷該模型是離散優化問題,在整場遊戲中對時間進行離散化處理,對每一秒通過上一秒進行模擬即可得到每一秒植物、殭屍、子彈的狀態,進而遞推整場遊戲的情況。因此首先應該構造該遊戲的模擬程序,其次再尋求解決改離散優化問題的算法。
好的,讓我們深入探討如何設計模擬仿真程序,以及如何通過算法設計和求解分析實現對《植物大戰殭屍》遊戲模型的優化。
1. 設計模擬仿真程序
1.1 程序架構
模擬仿真程序的架構可以劃分為以下幾個模塊:
-初始化模塊:初始化遊戲參數、植物和殭屍屬性、場地狀態等。
- 狀態更新模塊:模擬每一秒鐘的遊戲狀態,包括植物的生產和攻擊,殭屍的移動和攻擊等。
- 策略評估模塊:評估當前策略的效果,包括陽光數量、剩餘植物、殭屍情況等。
- 優化模塊:應用遺傳算法、動態規劃等方法優化策略。
1.2 初始化模塊
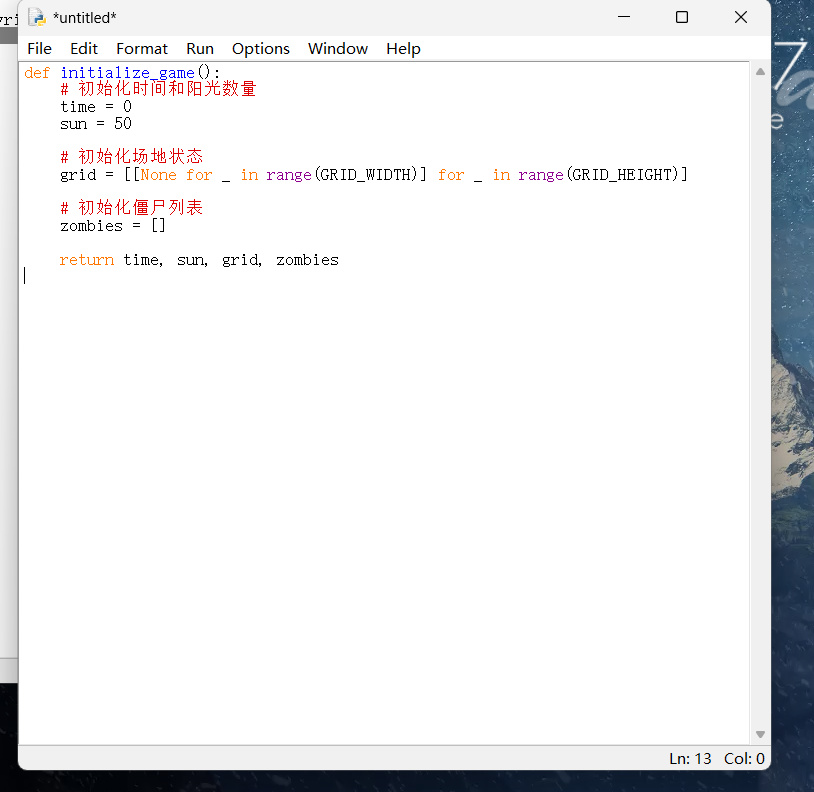
1.3 狀態更新模塊
1.4 策略評估模塊
2.算法設計
2.1 遺傳算法
2.2 動態規劃
3. 求解分析
3.1 模擬仿真
通過模擬遊戲中的每一秒,我們可以記錄下各種策略的表現,並通過統計分析找到最優策略。
3.2 遺傳算法
遺傳算法通過多代迭代優化策略,每一代都選擇表現較好的策略進行交叉和變異,從而逐步逼近最優解。
3.3 動態規劃
動態規劃通過將問題分解為子問題並存儲子問題的解來找到全局最優解,適用於確定性的遊戲過程。
最終結果,截止目前本人也在還在搗鼓中(果然數學會就是會,不會就是不會),大家有想法歡迎討論,我會認真研究的