随着植物大战僵尸杂交版的爆火,我也回想起小时候和父亲一起玩植物大战僵尸的日子,记得当时我特别喜欢把向日癸种在最左侧第一排,而父亲却喜欢将豌豆射手放在那儿,特别不能理解为什么,还时常询问老爸为什么。

现在上了大学突然意识到这个问题可能能通过数学建模完成,于是我就尝试了一下(不过我不是该专业方向的,有问题和想法也欢迎指正和讨论)
《植物大战僵尸》是一塔防类策略游戏,玩家在每一关卡中种植植物抵御各种僵尸入侵。
本文在分析植物大战僵尸人机博弈机制的基础上对博弈逻辑进行了模拟,通过遗传算法、动态规划求解植物大战僵尸一般通关模型,得到通关最优策略及最大阳光数量,并使用随机模拟及隐马尔科夫神经网络对 未知僵尸生成情况下的关卡进行模拟分析求解,
使用统计分析方法得到更复杂情况的最优策略及最大阳光数量期望。
1. 参数定义
1. 时间参数
t:时间,以秒为单位。
2. 场地参数
G:网格大小,表示游戏场地的行和列。
Gij:表示场地上第 i 行第 j 列的格子。
3. 植物参数
P:植物集合。
Pi:第 i 种植物。
C(Pi):种植植物 Pi 所需的阳光数量。
A(Pi):植物Pi 的攻击力。
R(Pi):植物Pi 的生产阳光速率(生产植物)。
H(Pi):植物Pi 的生命值。
4. 僵尸参数
Z:僵尸集合。
Zj:第 j 种僵尸。
S(Zjj):僵尸 Zj 的速度。
D(Zj):僵尸Zj 的耐久度(生命值)。
E(Zj):僵尸Zj 吃植物所需的时间。
5. 游戏参数
Y:当前阳光数量。
2. 通关模型建立
1. 状态定义
S(t):时间 t 时的游戏状态,包括植物位置、僵尸位置、阳光数量等。
2. 状态转移
植物生长:每秒生产植物增加阳光数量。
植物攻击:攻击植物对僵尸造成伤害,僵尸生命值减少。
僵尸移动:僵尸每秒向左移动一格。
僵尸攻击:僵尸吃掉植物,植物生命值减少。
3. 目标函数
最大化阳光数量:max∑t=0TY(t)\max \sum_{t=0}^{T} Y(t)max∑t=0TY(t)
通关条件:在所有僵尸到达最左侧前将其消灭。
4. 约束条件
植物种植:Y(t)≥C(Pi)Y(t) \geq C(P_i)Y(t)≥C(Pi)
植物生命:H(Pi,t)>0H(P_i, t) > 0H(Pi,t)>0
僵尸生命:D(Zj,t)≤0D(Z_j, t) \leq 0D(Zj,t)≤0
3. 最终模型建立
1. 遗传算法优化
初始化:生成初始种植策略集合。
适应度函数:根据阳光数量、通关时间等评估每个策略的优劣。
选择:选择适应度高的策略进行交叉和变异。
迭代:多次迭代,直到找到最优策略。
2. 动态规划求解
阶段划分:将游戏过程分为若干阶段,每个阶段为一个子问题。
状态定义:每个阶段的状态包括当前植物和僵尸的状态、阳光数量等。
状态转移:根据当前状态和决策转移到下一状态。
最优策略:通过动态规划找到每个阶段的最优策略,最终获得全局最优解。
3. 随机模拟
模拟过程:通过大量随机模拟评估不同策略的效果。
结果分析:统计分析不同策略在各种情况下的表现,找出最优策略和最大阳光数量期望。
4. 隐马尔科夫模型和神经网络预测
僵尸生成预测:结合隐马尔科夫模型和神经网络预测僵尸的生成模式。
策略调整:根据预测结果动态调整策略,提高通关成功率。
通过对上述模型的分析,可以判断该模型是离散优化问题,在整场游戏中对时间进行离散化处理,对每一秒通过上一秒进行模拟即可得到每一秒植物、僵尸、子弹的状态,进而递推整场游戏的情况。因此首先应该构造该游戏的模拟程序,其次再寻求解决改离散优化问题的算法。
好的,让我们深入探讨如何设计模拟仿真程序,以及如何通过算法设计和求解分析实现对《植物大战僵尸》游戏模型的优化。
1. 设计模拟仿真程序
1.1 程序架构
模拟仿真程序的架构可以划分为以下几个模块:
-初始化模块:初始化游戏参数、植物和僵尸属性、场地状态等。
- 状态更新模块:模拟每一秒钟的游戏状态,包括植物的生产和攻击,僵尸的移动和攻击等。
- 策略评估模块:评估当前策略的效果,包括阳光数量、剩余植物、僵尸情况等。
- 优化模块:应用遗传算法、动态规划等方法优化策略。
1.2 初始化模块
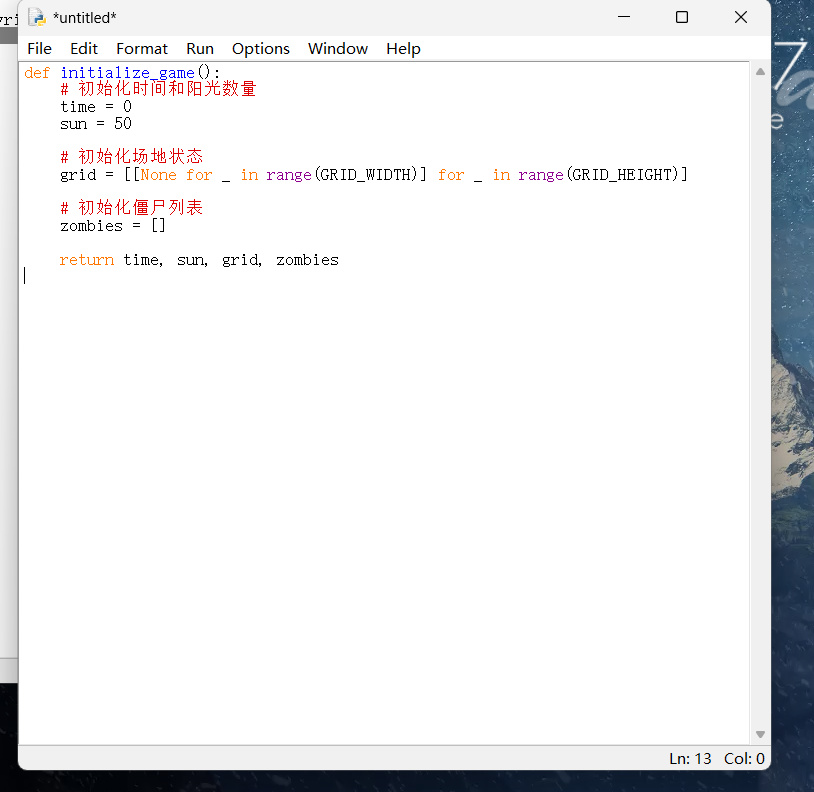
1.3 状态更新模块
1.4 策略评估模块
2.算法设计
2.1 遗传算法
2.2 动态规划
3. 求解分析
3.1 模拟仿真
通过模拟游戏中的每一秒,我们可以记录下各种策略的表现,并通过统计分析找到最优策略。
3.2 遗传算法
遗传算法通过多代迭代优化策略,每一代都选择表现较好的策略进行交叉和变异,从而逐步逼近最优解。
3.3 动态规划
动态规划通过将问题分解为子问题并存储子问题的解来找到全局最优解,适用于确定性的游戏过程。
最终结果,截止目前本人也在还在捣鼓中(果然数学会就是会,不会就是不会),大家有想法欢迎讨论,我会认真研究的