前言
如果說2025年春節期間有什麼關鍵詞,DeepSeek和AI肯定是其中之一。雖然敲一些關鍵字就能生成遊戲的時代還沒有完全到來,但AI確實在快速更新人們使用計算機和互聯網的方式。
以我個人體驗來說,目前DeepSeek在很多時候都是比百度和google更好的查資料來源(知識類、交通出行、概括總結等);雖然偶爾也有一些細節上的錯誤,但也可以通過對話指出其問題使其自動糾錯。
而在遊戲相關的領域,其實之前虛幻官方力推的基於照片掃描的三維重建(3D Reconstruction)就已經得到廣泛應用了。這是一項從前AI時代就開始提出的技術線,現在正在被AI深度學習狠狠地加持發展。如果說之前提這個事情還比較抽象的話,相信經歷了《黑神話:悟空》以後,大部分玩家應該也清楚了照片掃描能達到的效果。
AI三維重建的另外幾個方向,比如視頻生成、3D模型生成等也在不斷發展。在目前比較新的技術線上,其推算與生成的性能和準確度是由被稱為高斯點雲渲染(Gaussian Splatting)的算法來保證,而其在AI領域的更早期的技術是神經網絡輻照度場(NeRF)。這些可能都是我後面會讀到的內容——在這個系列的“上半場”應該都還不會讀到AI相關的內容,而是以一些基礎算法和理論為主。
至於AI生成圖象和動畫,以及從視頻進行動作捕捉等,目前已經進入了非常成熟足夠商用的階段了。但我個人的讀文章系列中可能不會涉及這兩部分。
對我個人而言,要基本看懂三維重建相關的內容還是難度不小的。目前這個系列我計劃在一年內以寫翻譯筆記的形式更新我的學習心得,如果有理解得不對的地方也歡迎指正。
為了趕時髦,我讓DeepSeek幫我總結了一下三維重建的一些關鍵點,構成了第一部分。另外還是老樣子,PPT部分以翻譯為主,打星號的部分是我的個人理解或補充。
一、三維重建的歷史脈絡
*這部分DeepSeek的概括我覺得足夠好了,因此就沒刪改(包括標點符號和樣式)——大家可以感受下。基本上我的三維重建粗讀計劃就是基於這些關鍵詞來進行的。
1. 早期探索(1960s-1970s)
- 計算機視覺的誕生:20世紀60年代,計算機視覺領域開始興起,研究者嘗試從二維圖像中提取三維信息。
- 基礎理論:70年代,研究者提出了許多基礎理論,如立體視覺(Stereo Vision)和結構光(Structured Light)技術。
2. 算法發展(1980s-1990s)
- 立體匹配:80年代,立體匹配算法得到顯著發展,研究者提出了多種匹配方法,如基於區域的匹配和基於特徵的匹配。
- 多視角幾何:90年代,多視角幾何理論逐漸成熟,研究者開始利用多張圖像進行三維重建。
3. 技術進步(2000s-2010s)
- 激光掃描:2000年代,激光掃描技術(LIDAR)被廣泛應用於三維重建,尤其是在建築和考古領域。
- 結構光與深度相機:2010年代,結構光和深度相機(如Microsoft Kinect)的出現,使得實時三維重建成為可能。
4. 深度學習與AI(2010s-至今)
- 深度學習:2010年代後期,深度學習技術被引入三維重建領域,顯著提高了重建的精度和效率。
- 自動化與實時重建:近年來,基於AI的三維重建算法能夠實現自動化和實時重建,廣泛應用於虛擬現實(VR)、增強現實(AR)和自動駕駛等領域。
5. 未來展望
- 高精度與實時性:未來,三維重建技術將繼續向高精度和實時性方向發展。
- 多模態融合:結合多種傳感器和數據源(如RGB圖像、深度圖像、激光掃描等)進行多模態融合,進一步提升重建效果。
三維重建技術的發展歷程反映了計算機視覺、傳感器技術和人工智能等多個領域的進步,未來有望在更多應用場景中發揮重要作用。
*這次讀立體視覺(Stereo Vision)我選擇了斯坦福大學Professor Fei-Fei Li 在2021年的課件。篇幅原因這次會讀其中的前半部分。
二、立體視覺概述——Introduction to stereo vision
*部分頁數顯示不連貫,可能是我抽選了一些頁,也有些是課件本身就沒標。
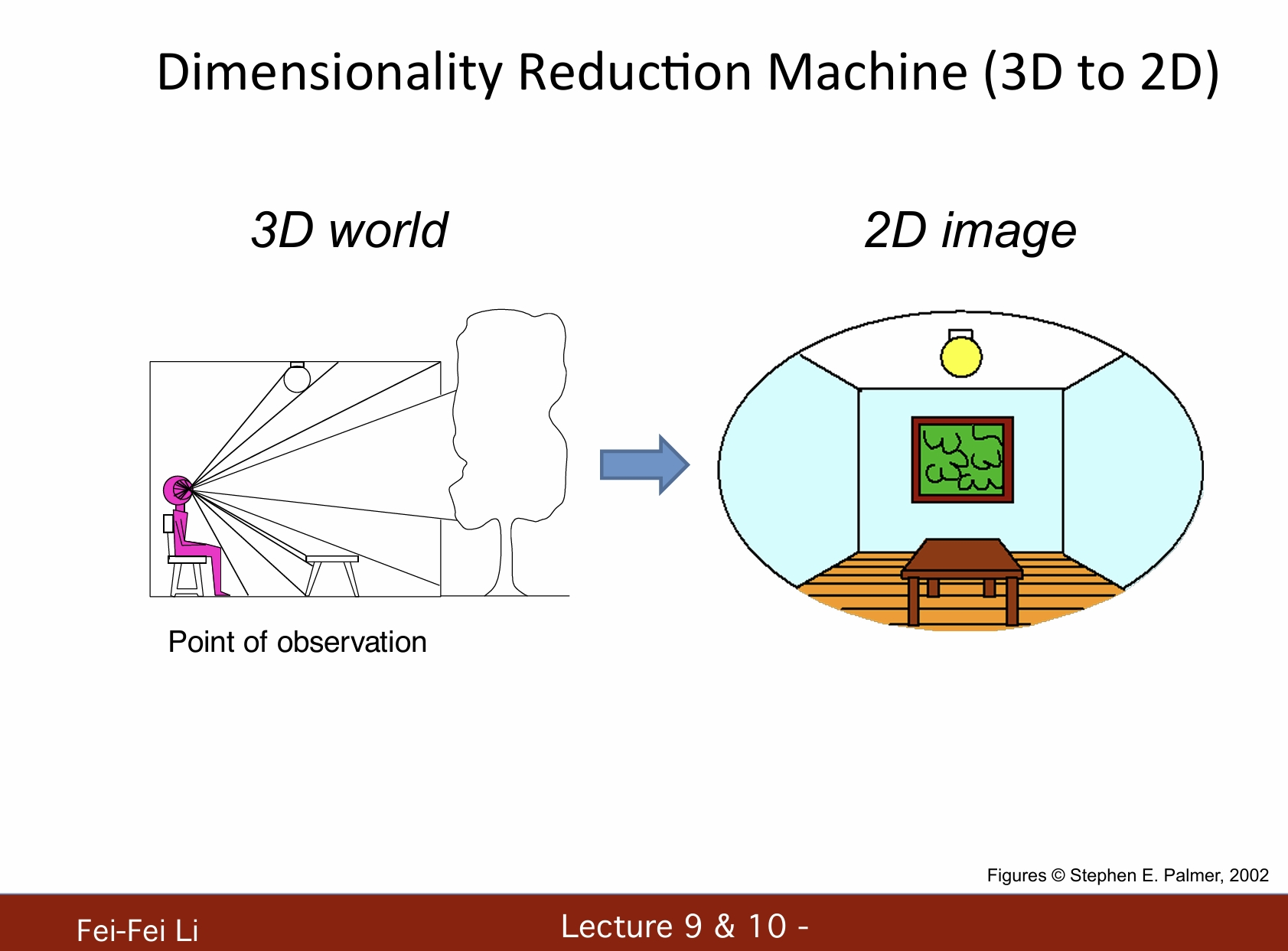
*這裡提出了降維機器(3D到2D)的概念,例如相機就是一種降維機器。
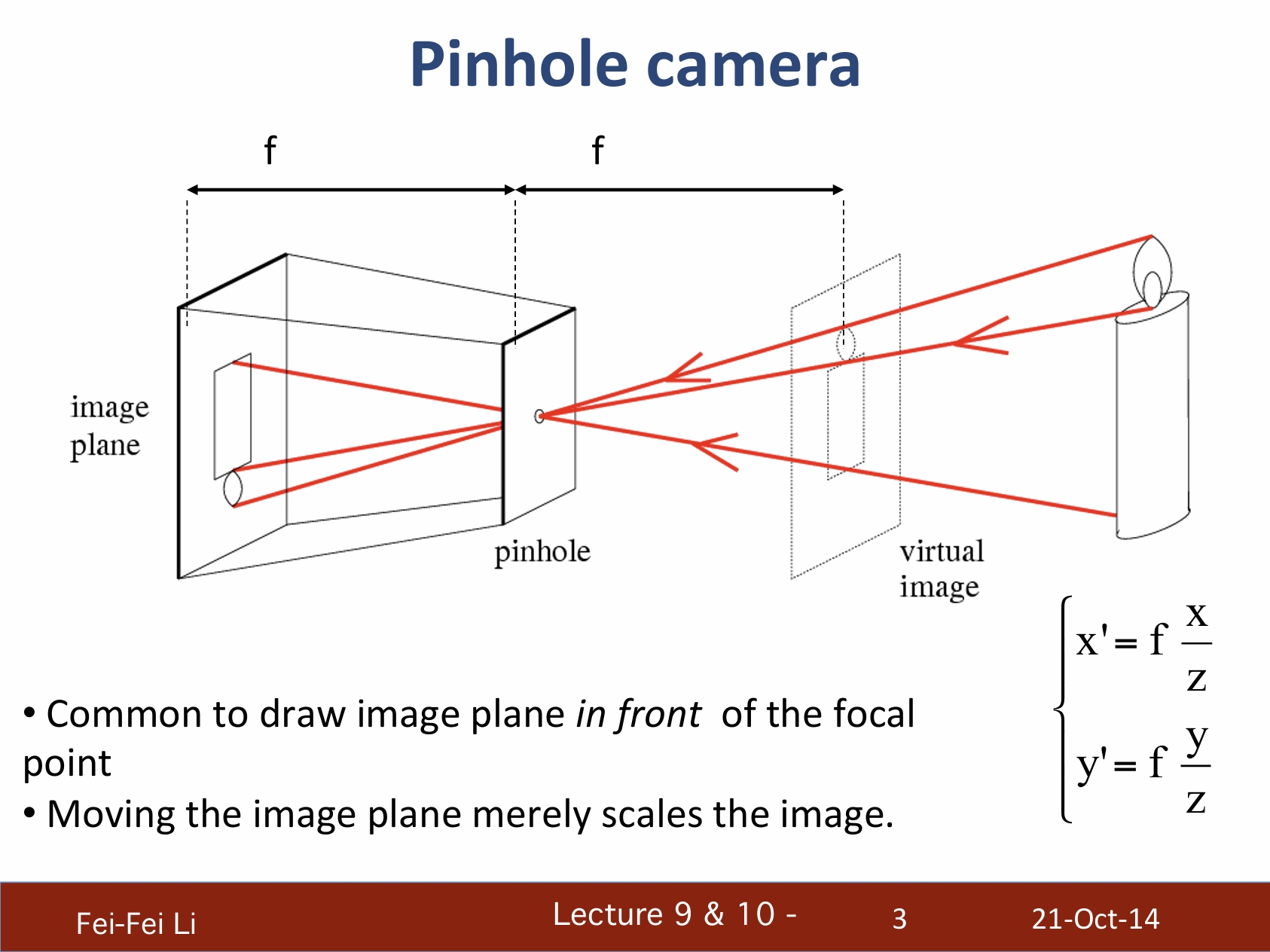
針孔相機(小孔成像)
- 能對焦點前方的範圍成像
- 移動成像平面能使圖像內容縮放
*圖中標出了在前後等距的位置可以視為有一個“虛擬圖像”,前後兩者是顛倒但是尺寸相同的。
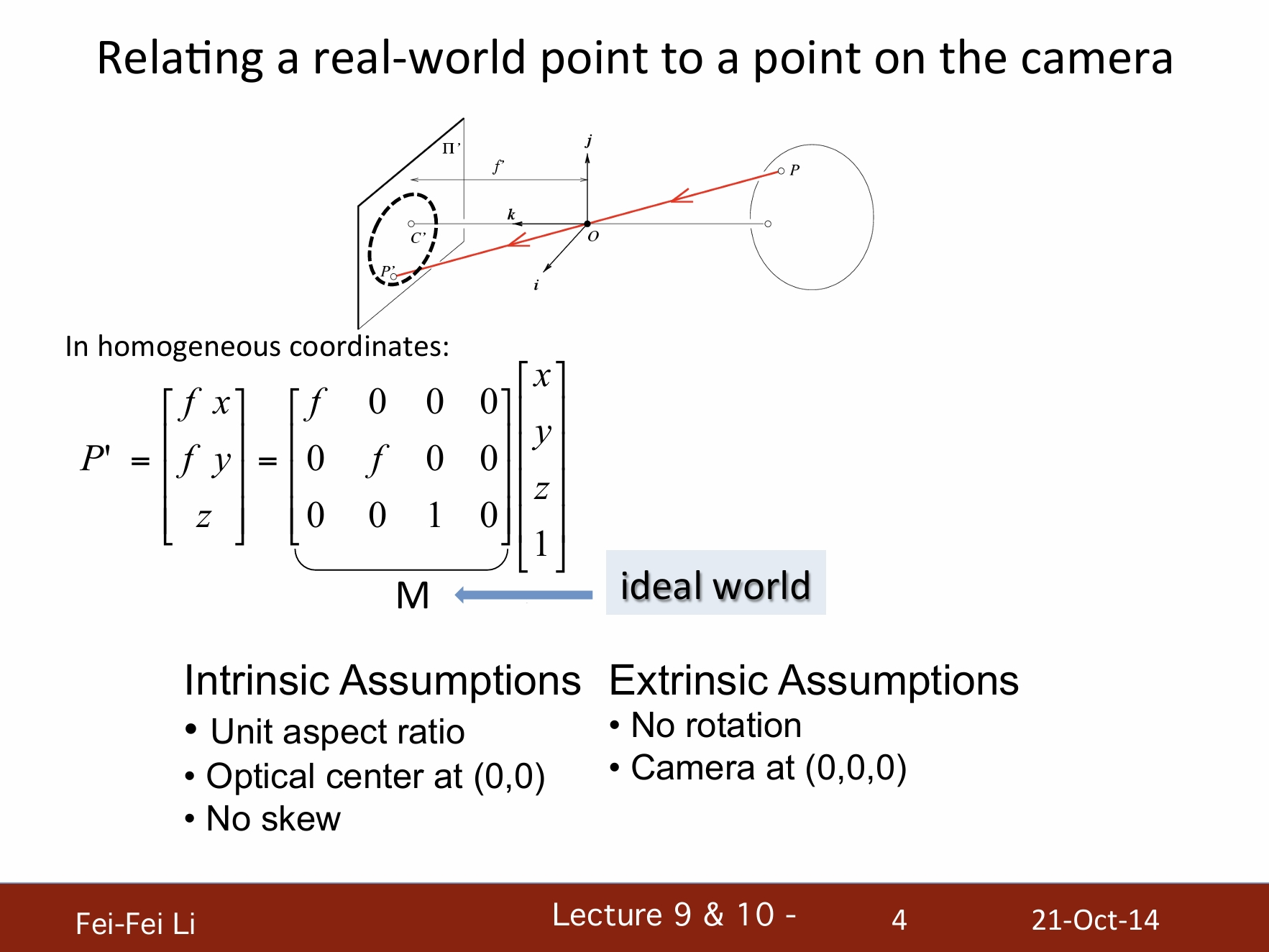
真實世界的點和攝像機中的點關聯
*這裡列出了一個基礎的齊次座標(homogeneous coordinates) 變換,其目的是計算真實世界的一點P是如何對應到成像平面的P'點的。其中XYZ是P的座標。
*這裡假設了變換矩陣M是一個“理想型”,即它符合這些預設:
- 內在假設:統一的縱橫比;光學中心在(0,0)點;沒有偏斜。
- 外在假設:沒有旋轉;攝像機在(0,0,0)點。
*齊次座標我還能聯想到的應用就是在遊戲引擎計算視錐體透視投影時。這裡附一張圖但是不展開了,有興趣的還是可以去看Games101。

*這裡矩陣K提出去,內部變成了單位矩陣I的形式。
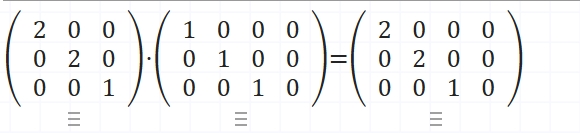
假設K=2,在矩陣計算器中還原了一下。

真實世界的攝像機
內在假設:光學中心在(u0,v0)點;矩形像素點陣;輕微的偏斜。
*這部分內在假設反映在變換矩陣中,u0、v0在矩陣中的位置用於計算平移,而α和β則反映了縱橫比的不統一,係數s則用於計算偏斜(扭曲)值。偏斜可以想象矩形扭成平行四邊形的情況。

真實世界的相機+真實世界的變換
外在假設:允許旋轉,攝像機在(tx,ty,tz)點。
*對應其中r系列的9個參數用來表示旋轉變換,而t系列3個參數表示攝像機的平移變換。
*至此內在假設和外在假設都變成了參數矩陣,並且兩者相乘也被賦予了意義。
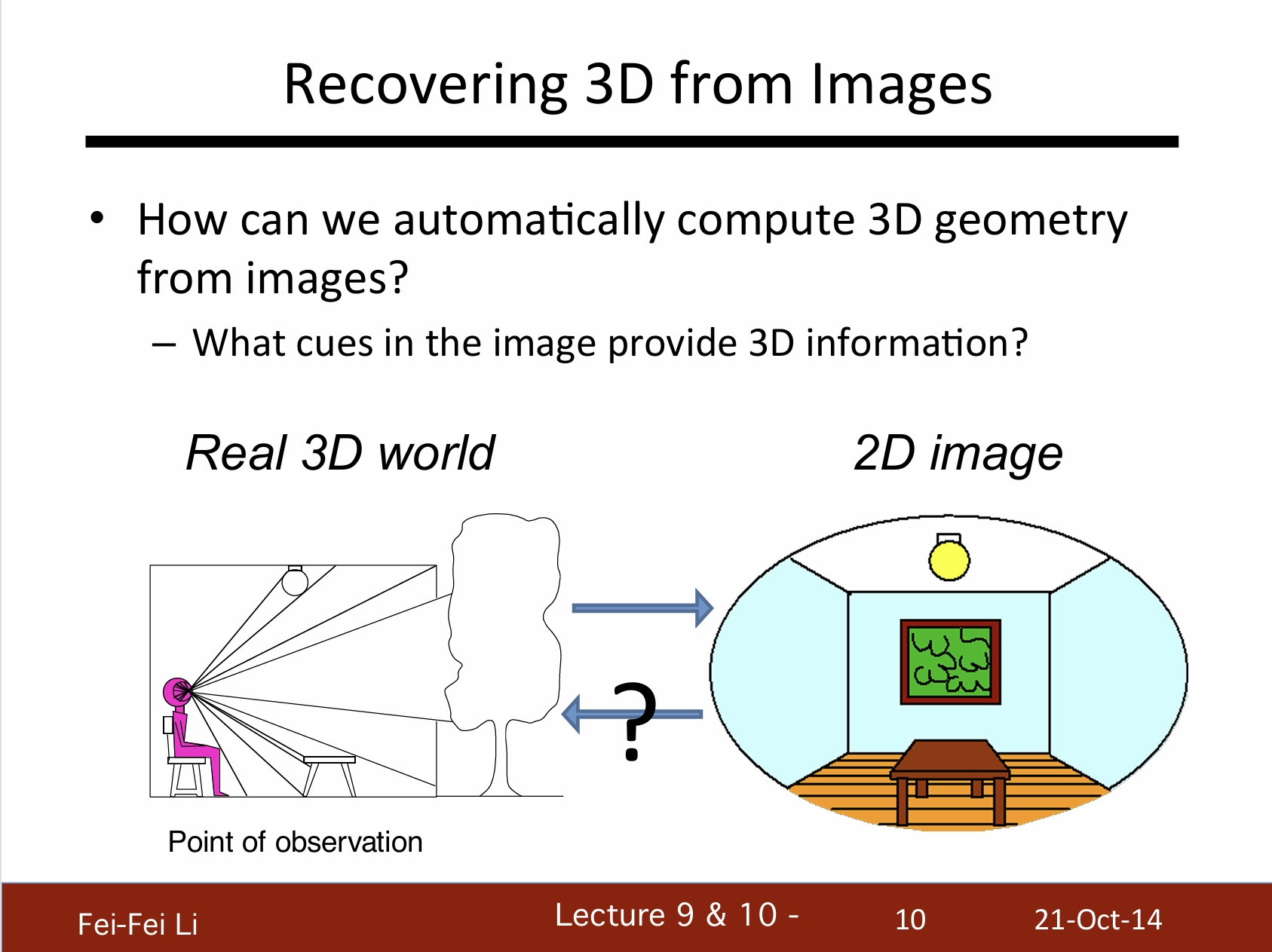
從圖像中還原3D
我們如何從圖像中計算3D幾何信息呢?——哪些圖像中的線索能提供3D信息?
明暗
*圖中的這個公司Merle Norman Cosmetics是一個換妝品牌子,和主題無關。

紋理
*這裡指有一定規律的紋理走向。

焦點

動態

其它:高光、陰影、剪影、內反射、對稱型、光學偏振等。
課件中會聚焦在motion這一類線索——追蹤圖像中某些特徵點在不同圖像空間的位置。
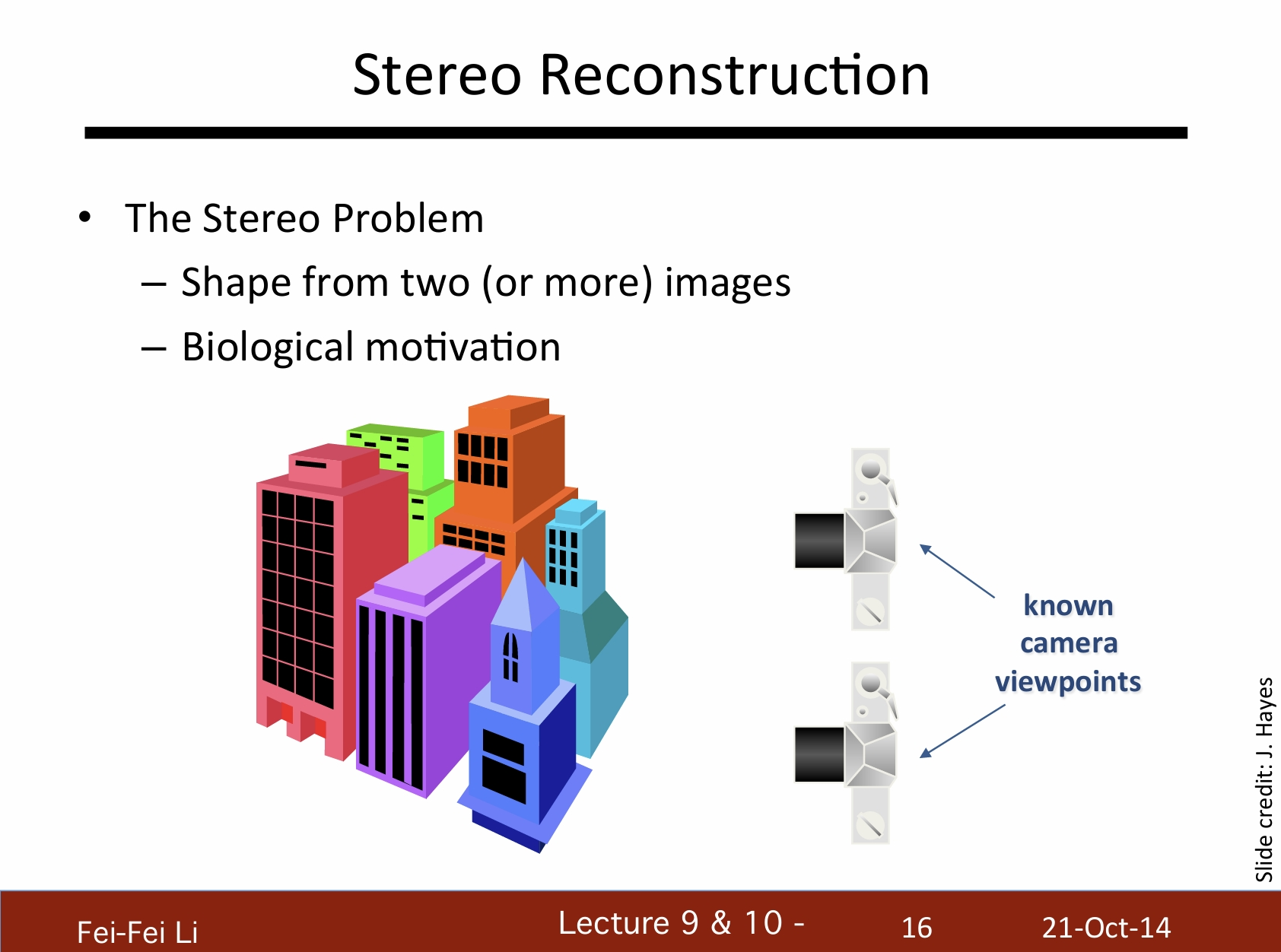
立體重建
立體課題(指為什麼要使用多視角):
- 通過兩張(或更多)圖片生成形體
- 生物性動機(人眼)

1. 二比一更好

2. 從匯聚點還原深度
*基於人眼可以感受雙眼夾角的原理,通過圖中的公式就可以計算出距離。
三、對極幾何的簡單引入——Epipolar geometry: a gentle intro
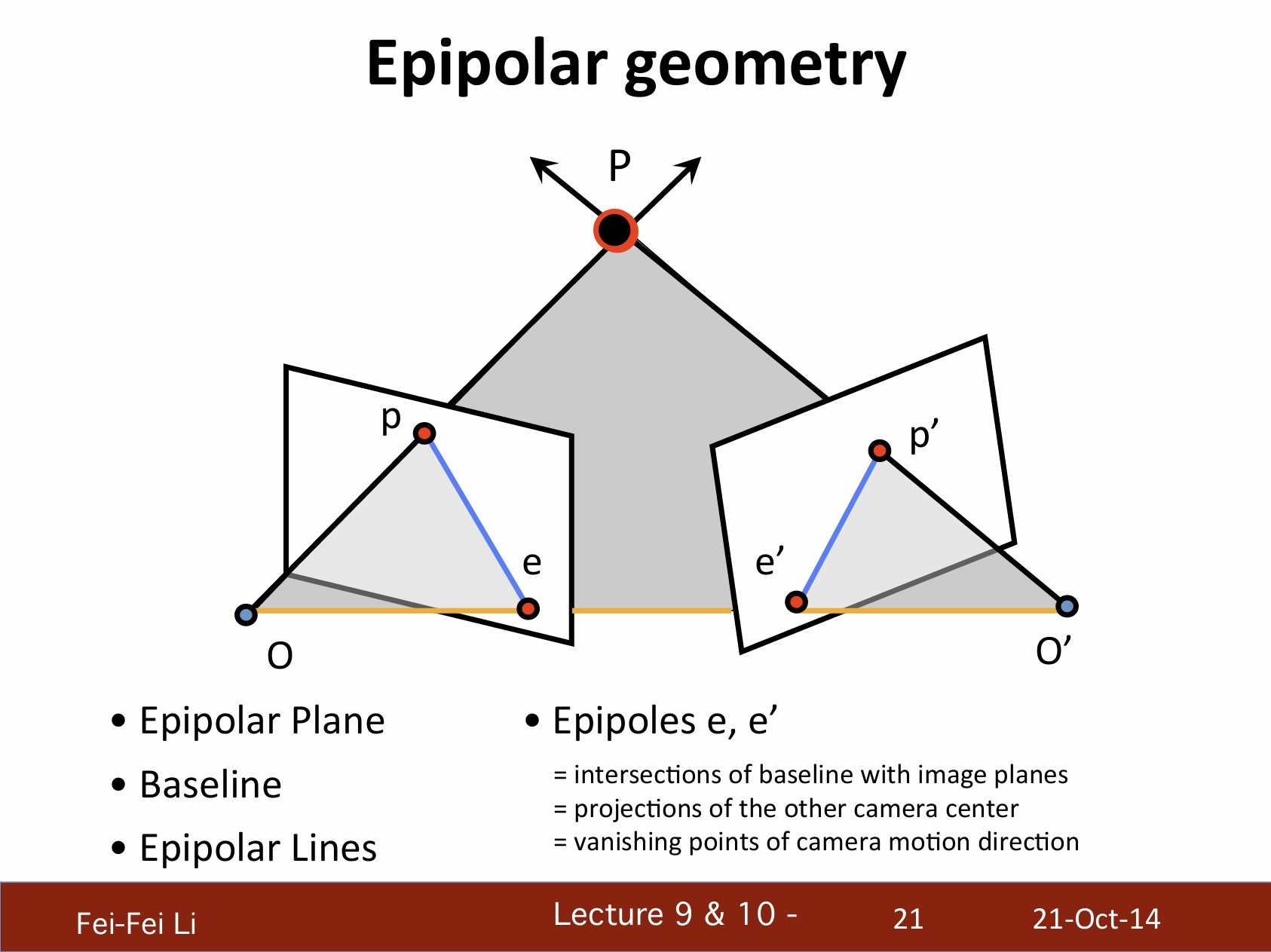
對極幾何
*這裡引入了幾個基本概念:對極平面、基線(黃色)、對極線。
*其中極點e、e'表示:
- 基線和圖像平面的交點
- 另一攝像機中心的投影
- 攝像機動態方向的消失點

例子:匯聚圖像平面

對極約束
- 同一個物體的不同視角
- 假設已知攝像機的位置和矩陣
- 給定一個左側圖片的點,如何確定右側圖片中該點的位置?
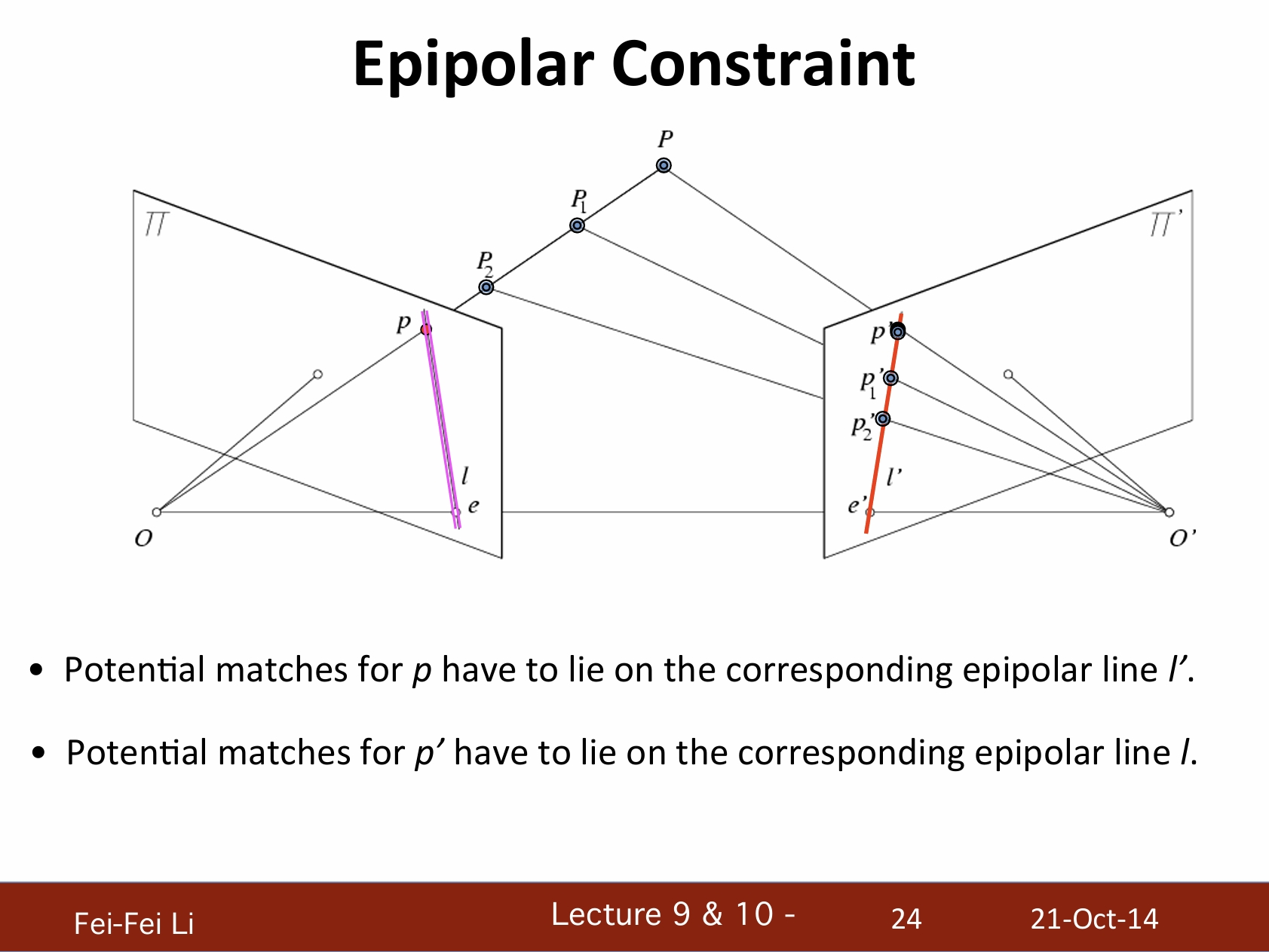
- p點的潛在匹配點必須在對應的極線l'上。
- p'點的潛在匹配點必須在對應的極線l。
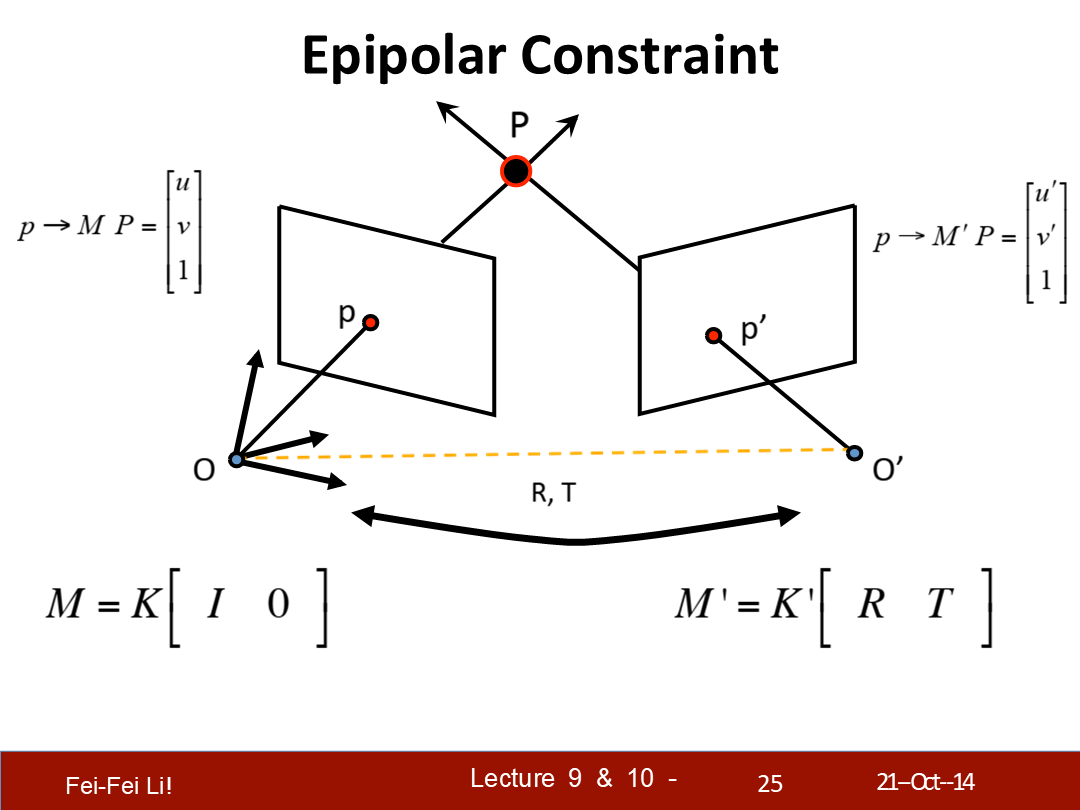
*圖中右側上方應該是p'點,課件應該是寫錯了。p和p'都是在各自圖像平面上投影的點。
*M是左側攝像機對應的矩陣,寫成了之前一節中的形式,K對應之前提到的內部假設,後面的單位陣I是默認旋轉矩陣、0則是默認位移矩陣。
*M'則是經過了旋轉R和平移T之後的攝像機矩陣。
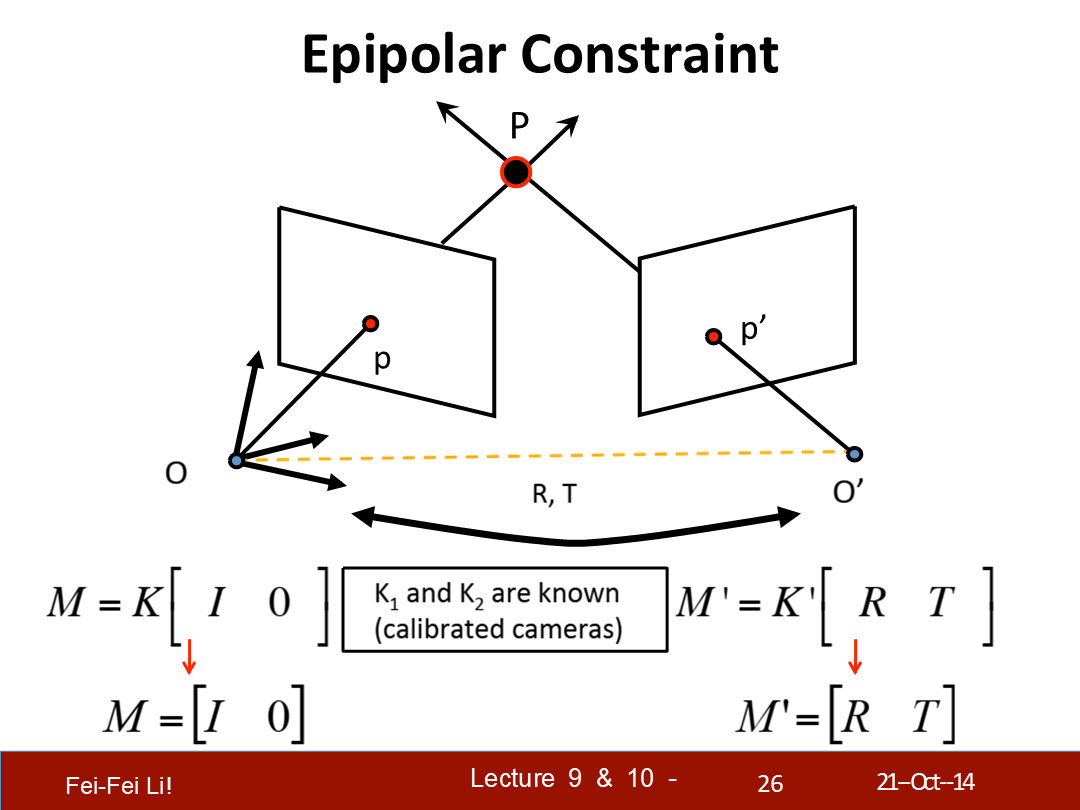
*兩者的K值是由校準相機(calibrated camera)的參數來確保的。
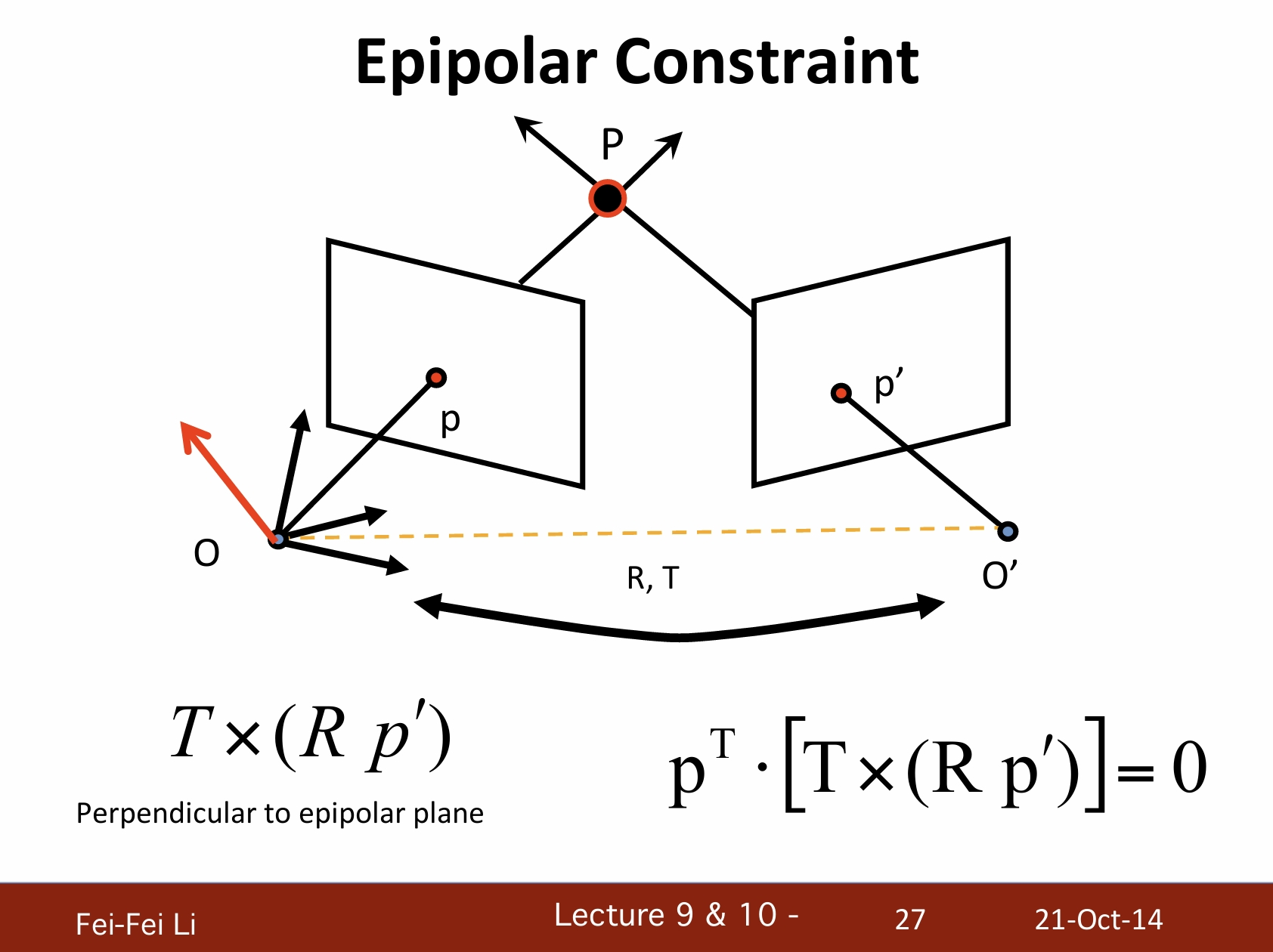
*T叉乘(Rp')得到的向量與對極平面垂直。
*p的轉置與之的點乘等於0——代表兩者也垂直。矩陣的轉置可以理解為將其行列翻轉的結果。
*向量點乘得到的是一個標量,而叉乘得到的是一個與兩者垂直的法向量。

向量叉乘轉為矩陣乘法
*這裡引入了一個斜對稱矩陣的概念,其對角線上值為0,其它位置的值分佈如圖。
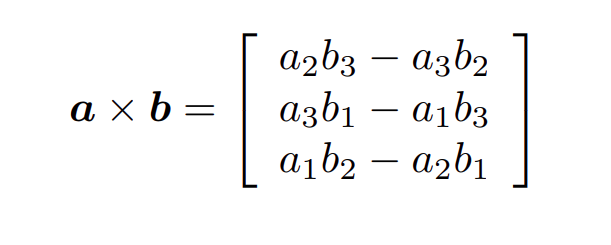
作為參照這裡展示了向量叉乘的計算結果
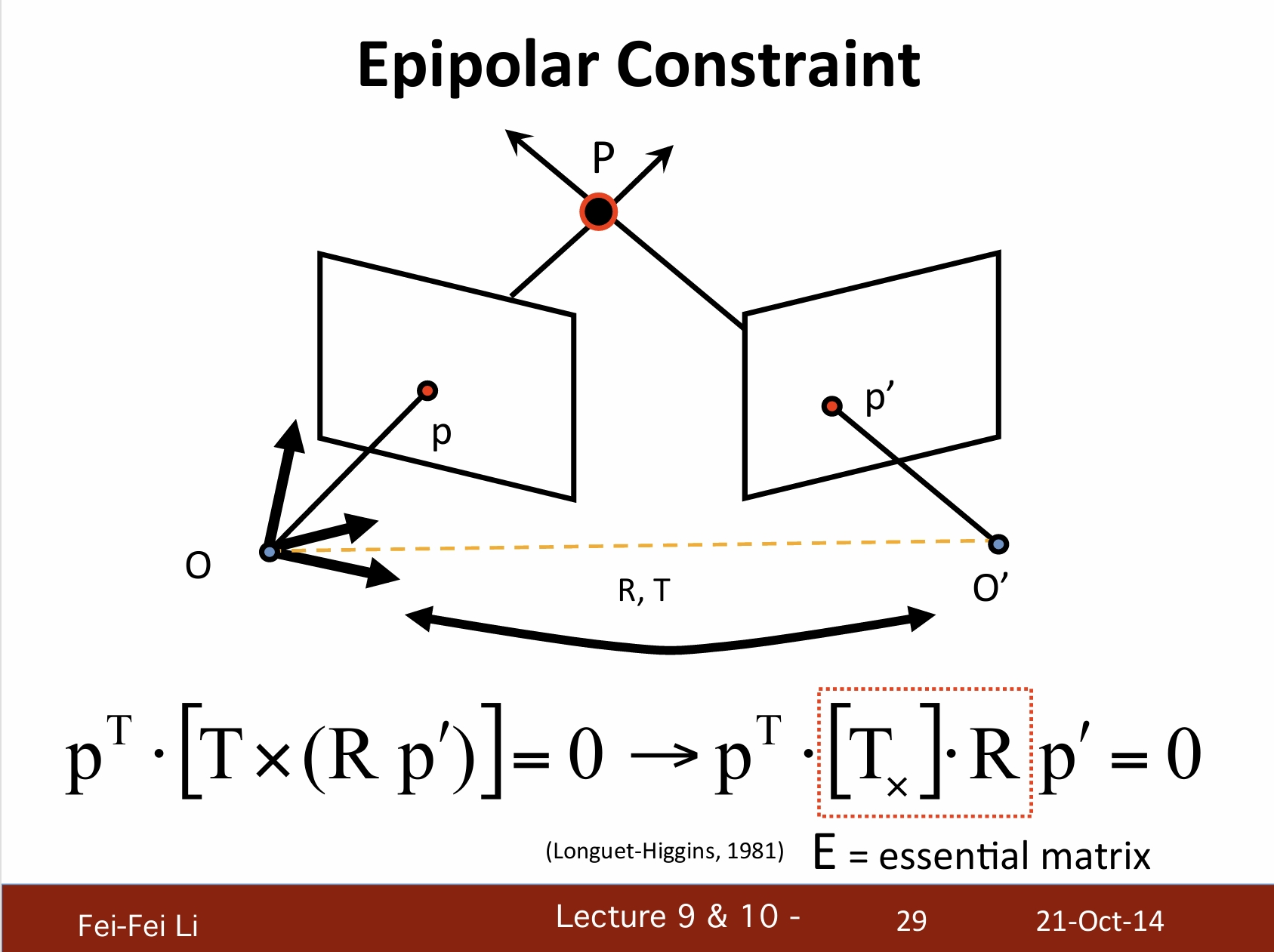
*將之前叉乘的部分轉換為矩陣點乘,其中提出的部分被稱為本質矩陣。通過它可以快速運算出另一個圖像中的極線。
*這一概念於1981年由Higgins提出,這一概念的翻譯也在矩陣學中被廣泛使用。
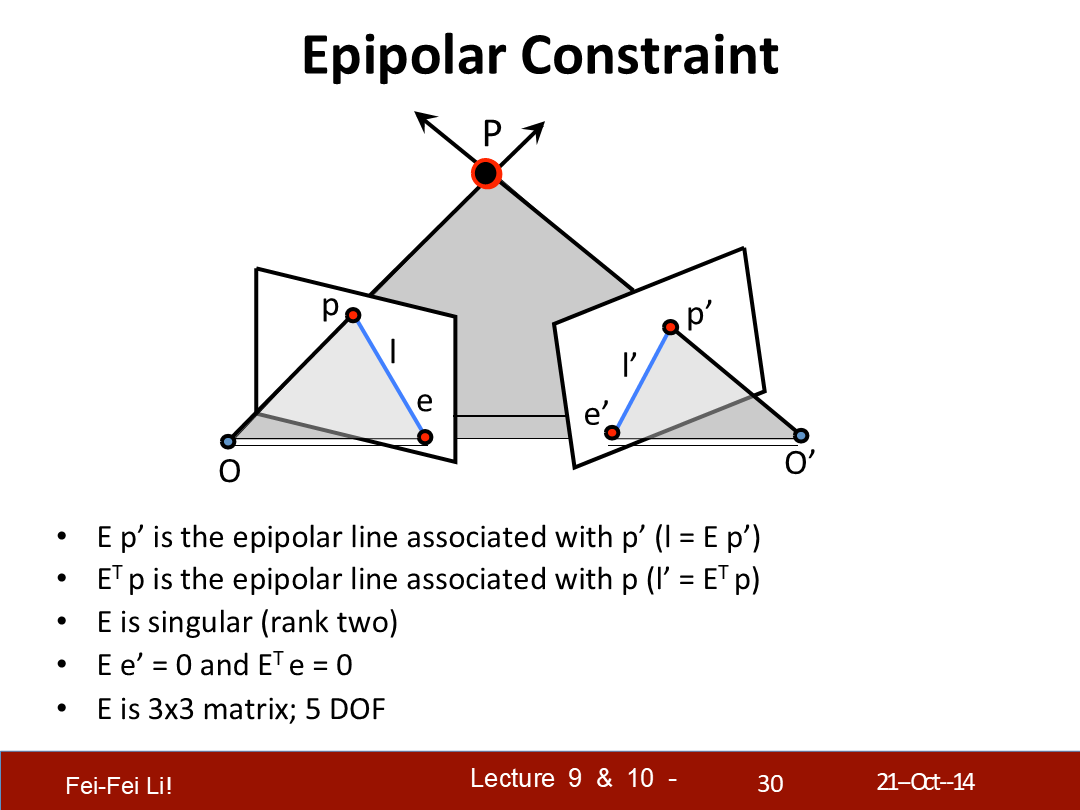
本質矩陣的一些特質如下:
- E乘p'是與p'相關的極限l。
- “E的轉置”乘p是與p對應極線p'。
- E是一個奇異矩陣。它沒有逆矩陣,並有著EX=0有無限多解的特性。
- E乘e'等於0,E的轉置乘e等於0。(這類計算時e和e'視為向量)
- E是一個3X3的矩陣,它有著5的自由度。
*DOF是degree of freedom的縮寫,以通俗但不算準確的方式來描述,矩陣自由度值有其中最少多少個參數能確定其約束;又由於對極約束是等式為零的約束,所以對E乘以任意非零常數後,對極約束仍然滿足——這件事情稱為E在不同尺度下是等價的。 基於平移3個參數、旋轉3個參數,尺度等價減1(指其它參數可以按一個參數做等比例縮放),得到自由度為5。
四、平行圖片與圖像校正——Parallel images & image rectification
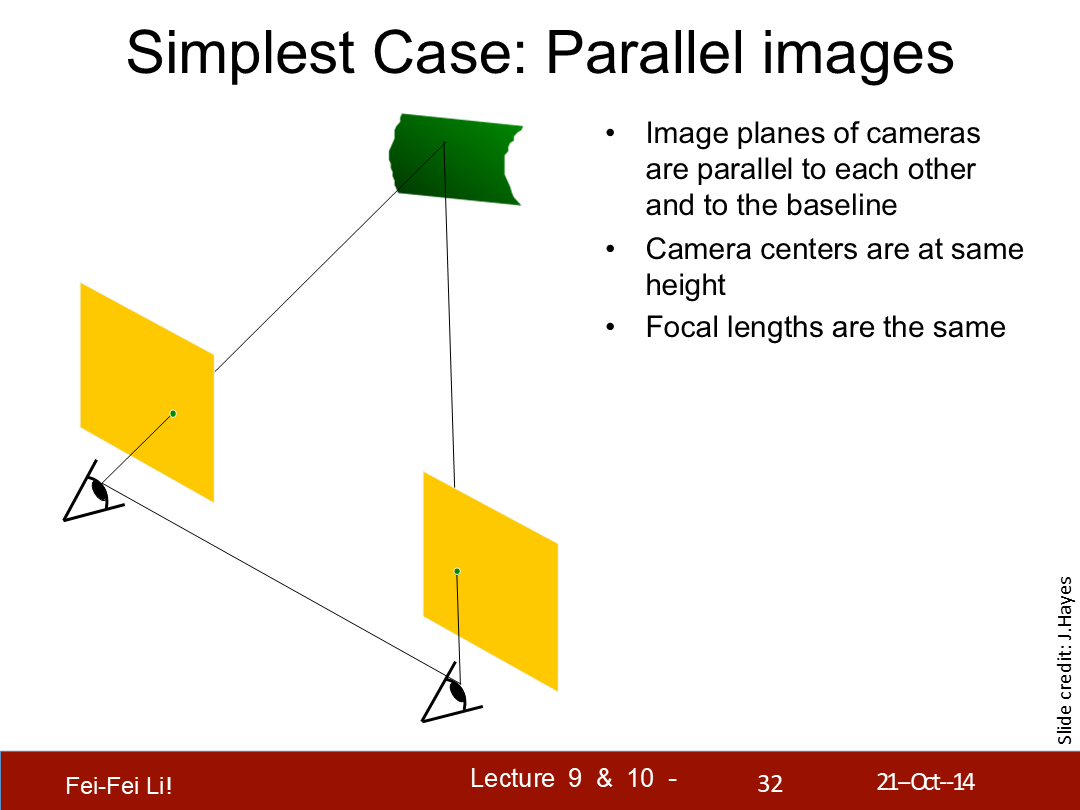
最簡單的例子——平行圖片
- 攝像機的圖像平面彼此平行並與基線平行
- 攝像機中心在同一高度
- 焦距相同
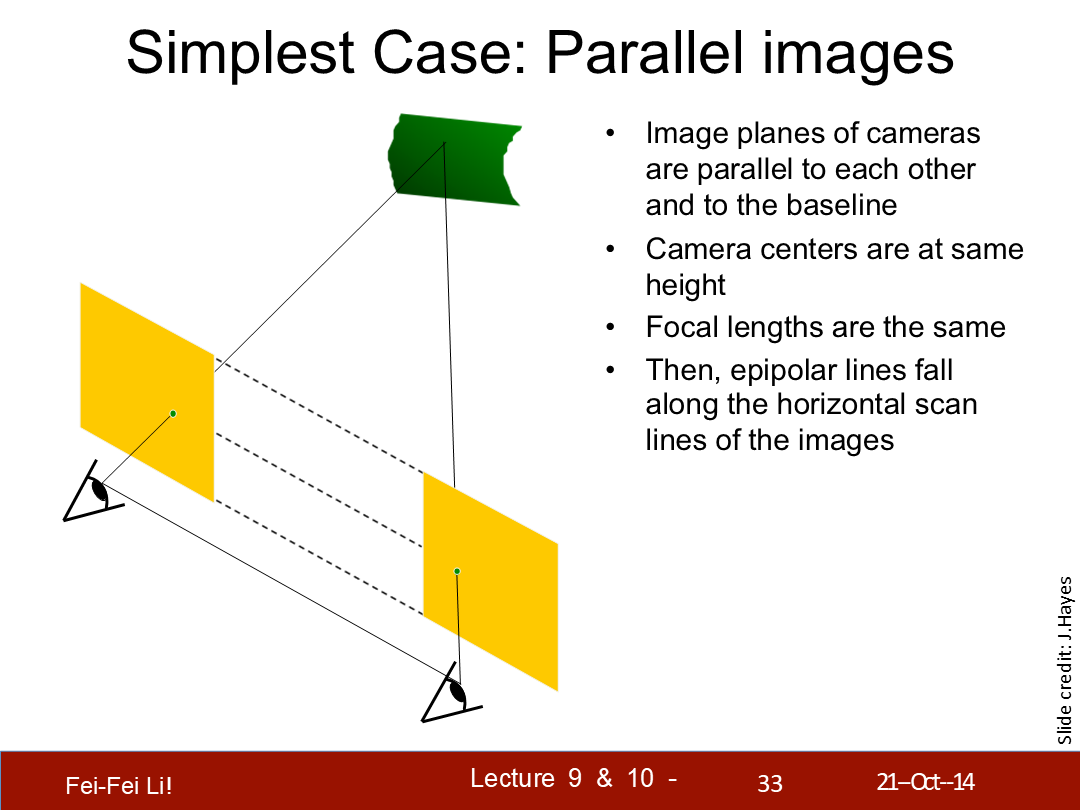
此時,極線就沿著圖片的水平掃描線分佈。

平行圖片的本質矩陣
*這裡將t按照之前的規則轉換成斜對角矩陣[tx],而R是單位矩陣——這樣就得到E。

*由於矩陣乘是有結合律的,因此可以得出v=v'的結論,即圖中所說的對應兩點的y座標相同。
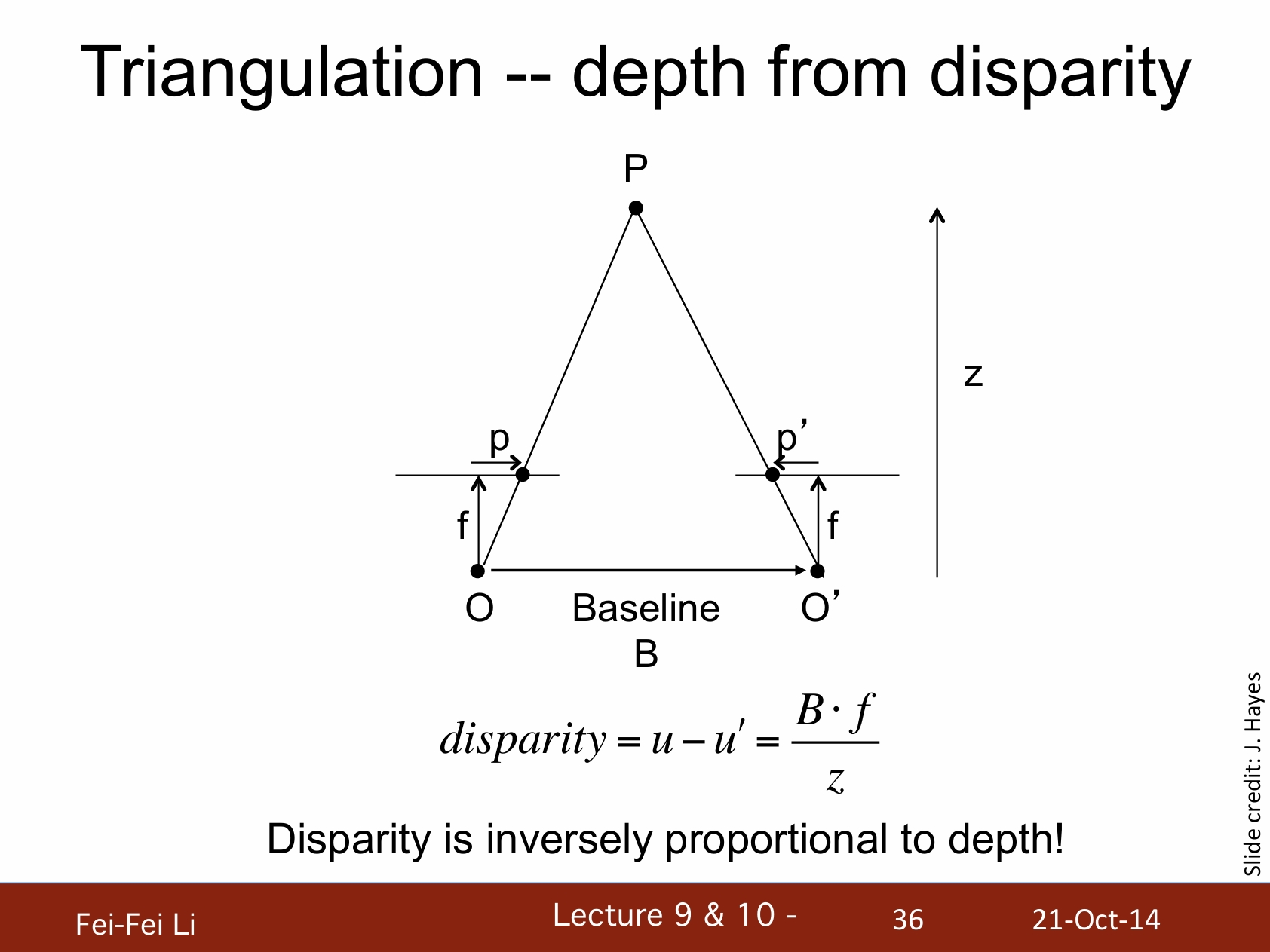
三角測量——依據差異計算深度
*差異(disparity)值是和深度成反比的。
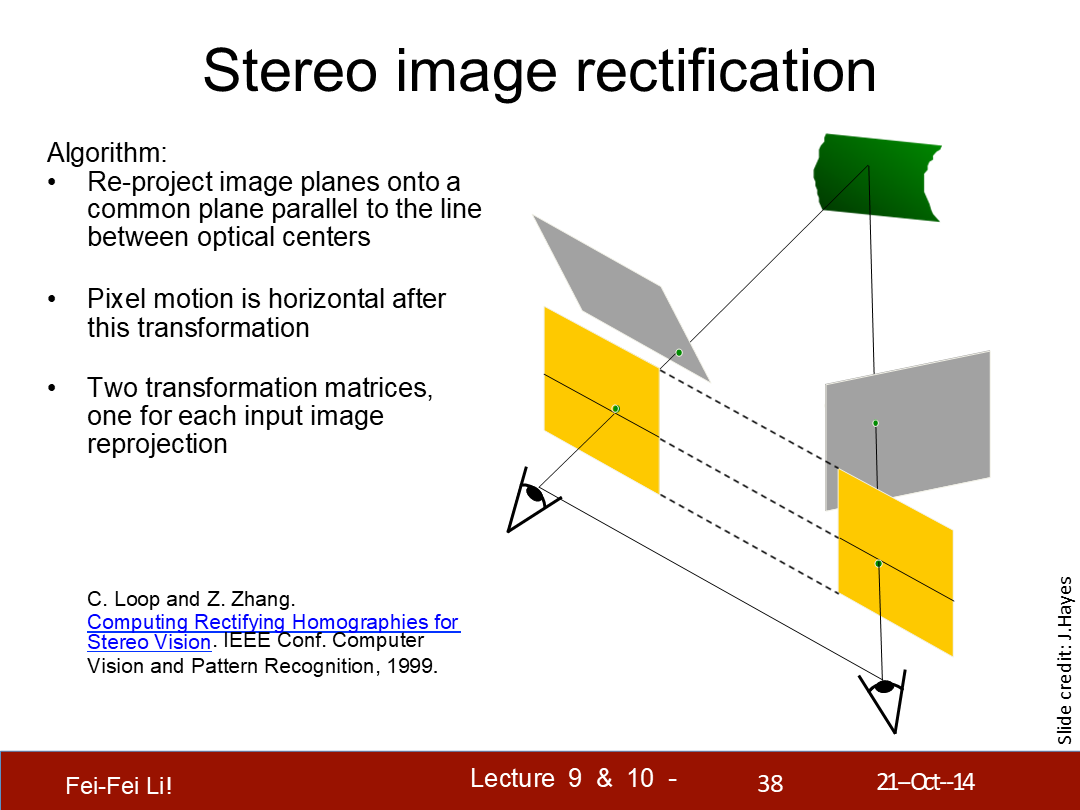
立體圖像校正
算法:
- 重投影圖像平面,至兩個與視覺光學中心線平行的平面上。
- 這次變化之後像素的移動是水平的。
- 兩個變換矩陣,對應每個輸入圖片的投影各一個。
*直譯過來稍微有些彆扭,但結合示意圖理解,實際上是想用多一個步驟的圖像平面變換來達到簡化計算以及利用三角測量的意義。

校準示例

應用:視覺變形

移除透視扭曲(校正)
結語
由於課件沒有解說稿,因此能感覺到有些部分直接上各種公式計算還是缺一點鋪墊。而如此高密度的各種矩陣計算,有些我能掌握,也有很多方面我是純萌新——有些東西只能概念性的把握一下,沒法深入再去了解了。
但儘管如此,相信不管是我還是讀到這裡的各位,應該能從示意圖感受到這些計算機視覺領域的前期研究是在處理哪些方面的問題,併為之設計了哪些數學工具和算法的。
儘管只是開了個頭,距離讀到最前沿和AI都還挺遠,但也算是開啟了這個讀計算機視覺和三維重建方面文章的系列。下週會繼續更新這篇課件的下半部分。
最後是一些資料鏈接:
立體視覺的WIKI
一篇介紹本質矩陣的知乎
一個實用的矩陣計算器工具
介紹攝像機校準的一篇文章
斯坦福大學這篇課件的地址