前言
如果说2025年春节期间有什么关键词,DeepSeek和AI肯定是其中之一。虽然敲一些关键字就能生成游戏的时代还没有完全到来,但AI确实在快速更新人们使用计算机和互联网的方式。
以我个人体验来说,目前DeepSeek在很多时候都是比百度和google更好的查资料来源(知识类、交通出行、概括总结等);虽然偶尔也有一些细节上的错误,但也可以通过对话指出其问题使其自动纠错。
而在游戏相关的领域,其实之前虚幻官方力推的基于照片扫描的三维重建(3D Reconstruction)就已经得到广泛应用了。这是一项从前AI时代就开始提出的技术线,现在正在被AI深度学习狠狠地加持发展。如果说之前提这个事情还比较抽象的话,相信经历了《黑神话:悟空》以后,大部分玩家应该也清楚了照片扫描能达到的效果。
AI三维重建的另外几个方向,比如视频生成、3D模型生成等也在不断发展。在目前比较新的技术线上,其推算与生成的性能和准确度是由被称为高斯点云渲染(Gaussian Splatting)的算法来保证,而其在AI领域的更早期的技术是神经网络辐照度场(NeRF)。这些可能都是我后面会读到的内容——在这个系列的“上半场”应该都还不会读到AI相关的内容,而是以一些基础算法和理论为主。
至于AI生成图象和动画,以及从视频进行动作捕捉等,目前已经进入了非常成熟足够商用的阶段了。但我个人的读文章系列中可能不会涉及这两部分。
对我个人而言,要基本看懂三维重建相关的内容还是难度不小的。目前这个系列我计划在一年内以写翻译笔记的形式更新我的学习心得,如果有理解得不对的地方也欢迎指正。
为了赶时髦,我让DeepSeek帮我总结了一下三维重建的一些关键点,构成了第一部分。另外还是老样子,PPT部分以翻译为主,打星号的部分是我的个人理解或补充。
一、三维重建的历史脉络
*这部分DeepSeek的概括我觉得足够好了,因此就没删改(包括标点符号和样式)——大家可以感受下。基本上我的三维重建粗读计划就是基于这些关键词来进行的。
1. 早期探索(1960s-1970s)
- 计算机视觉的诞生:20世纪60年代,计算机视觉领域开始兴起,研究者尝试从二维图像中提取三维信息。
- 基础理论:70年代,研究者提出了许多基础理论,如立体视觉(Stereo Vision)和结构光(Structured Light)技术。
2. 算法发展(1980s-1990s)
- 立体匹配:80年代,立体匹配算法得到显著发展,研究者提出了多种匹配方法,如基于区域的匹配和基于特征的匹配。
- 多视角几何:90年代,多视角几何理论逐渐成熟,研究者开始利用多张图像进行三维重建。
3. 技术进步(2000s-2010s)
- 激光扫描:2000年代,激光扫描技术(LIDAR)被广泛应用于三维重建,尤其是在建筑和考古领域。
- 结构光与深度相机:2010年代,结构光和深度相机(如Microsoft Kinect)的出现,使得实时三维重建成为可能。
4. 深度学习与AI(2010s-至今)
- 深度学习:2010年代后期,深度学习技术被引入三维重建领域,显著提高了重建的精度和效率。
- 自动化与实时重建:近年来,基于AI的三维重建算法能够实现自动化和实时重建,广泛应用于虚拟现实(VR)、增强现实(AR)和自动驾驶等领域。
5. 未来展望
- 高精度与实时性:未来,三维重建技术将继续向高精度和实时性方向发展。
- 多模态融合:结合多种传感器和数据源(如RGB图像、深度图像、激光扫描等)进行多模态融合,进一步提升重建效果。
三维重建技术的发展历程反映了计算机视觉、传感器技术和人工智能等多个领域的进步,未来有望在更多应用场景中发挥重要作用。
*这次读立体视觉(Stereo Vision)我选择了斯坦福大学Professor Fei-Fei Li 在2021年的课件。篇幅原因这次会读其中的前半部分。
二、立体视觉概述——Introduction to stereo vision
*部分页数显示不连贯,可能是我抽选了一些页,也有些是课件本身就没标。
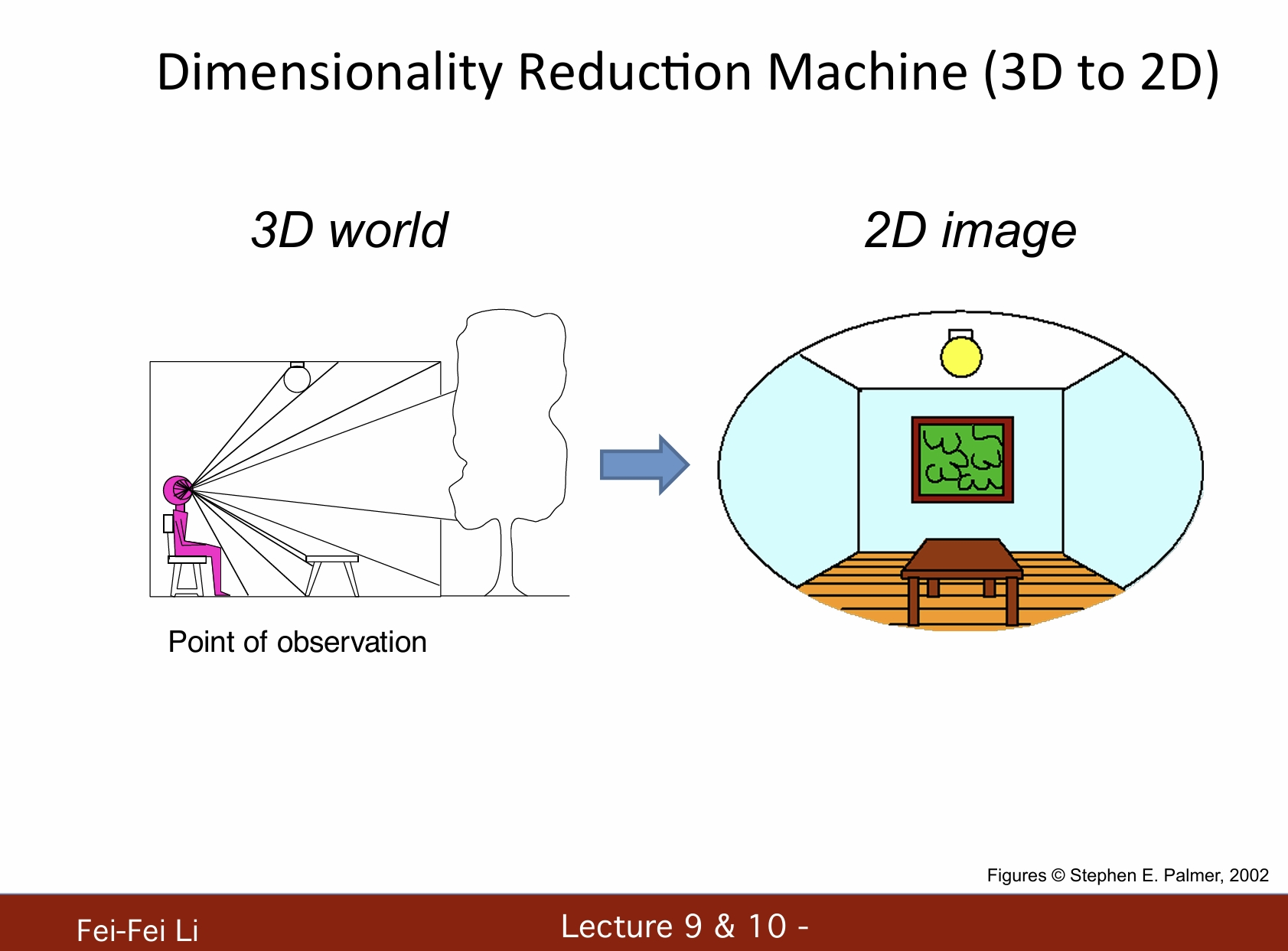
*这里提出了降维机器(3D到2D)的概念,例如相机就是一种降维机器。
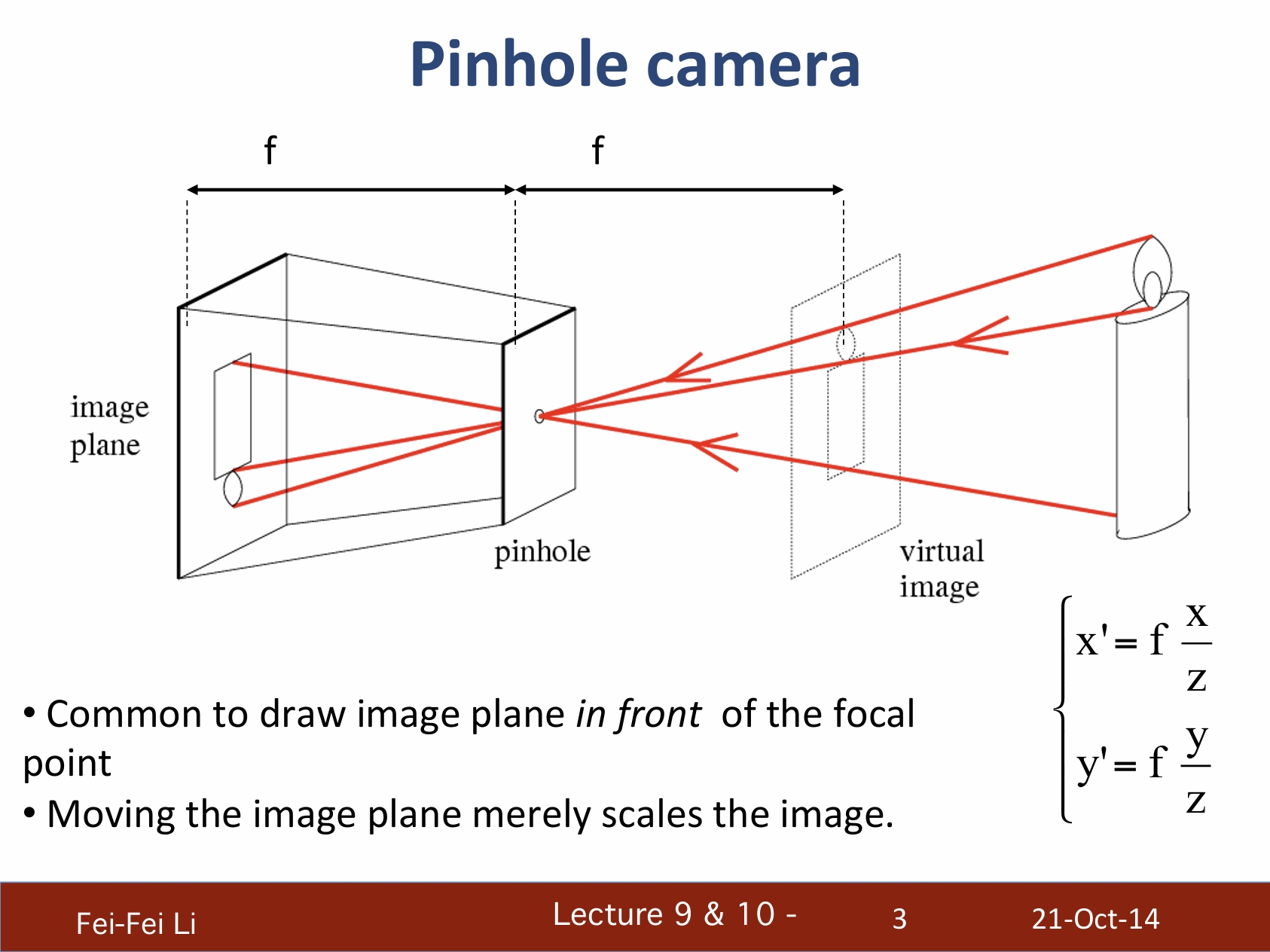
针孔相机(小孔成像)
- 能对焦点前方的范围成像
- 移动成像平面能使图像内容缩放
*图中标出了在前后等距的位置可以视为有一个“虚拟图像”,前后两者是颠倒但是尺寸相同的。
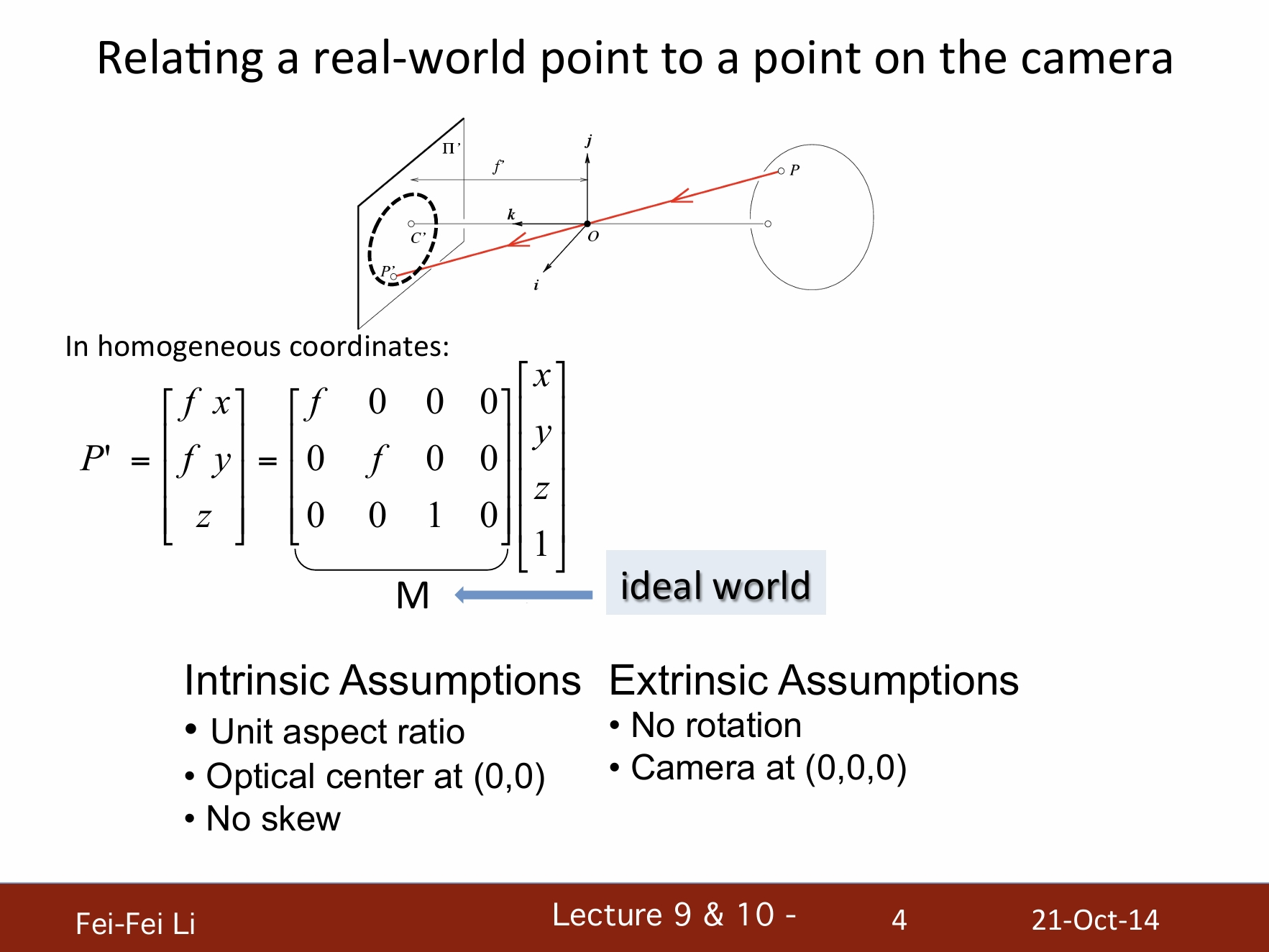
真实世界的点和摄像机中的点关联
*这里列出了一个基础的齐次坐标(homogeneous coordinates) 变换,其目的是计算真实世界的一点P是如何对应到成像平面的P'点的。其中XYZ是P的坐标。
*这里假设了变换矩阵M是一个“理想型”,即它符合这些预设:
- 内在假设:统一的纵横比;光学中心在(0,0)点;没有偏斜。
- 外在假设:没有旋转;摄像机在(0,0,0)点。
*齐次坐标我还能联想到的应用就是在游戏引擎计算视锥体透视投影时。这里附一张图但是不展开了,有兴趣的还是可以去看Games101。

*这里矩阵K提出去,内部变成了单位矩阵I的形式。
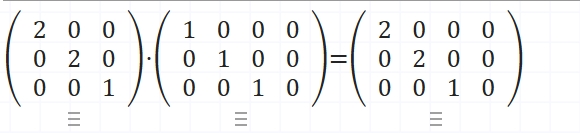
假设K=2,在矩阵计算器中还原了一下。

真实世界的摄像机
内在假设:光学中心在(u0,v0)点;矩形像素点阵;轻微的偏斜。
*这部分内在假设反映在变换矩阵中,u0、v0在矩阵中的位置用于计算平移,而α和β则反映了纵横比的不统一,系数s则用于计算偏斜(扭曲)值。偏斜可以想象矩形扭成平行四边形的情况。

真实世界的相机+真实世界的变换
外在假设:允许旋转,摄像机在(tx,ty,tz)点。
*对应其中r系列的9个参数用来表示旋转变换,而t系列3个参数表示摄像机的平移变换。
*至此内在假设和外在假设都变成了参数矩阵,并且两者相乘也被赋予了意义。
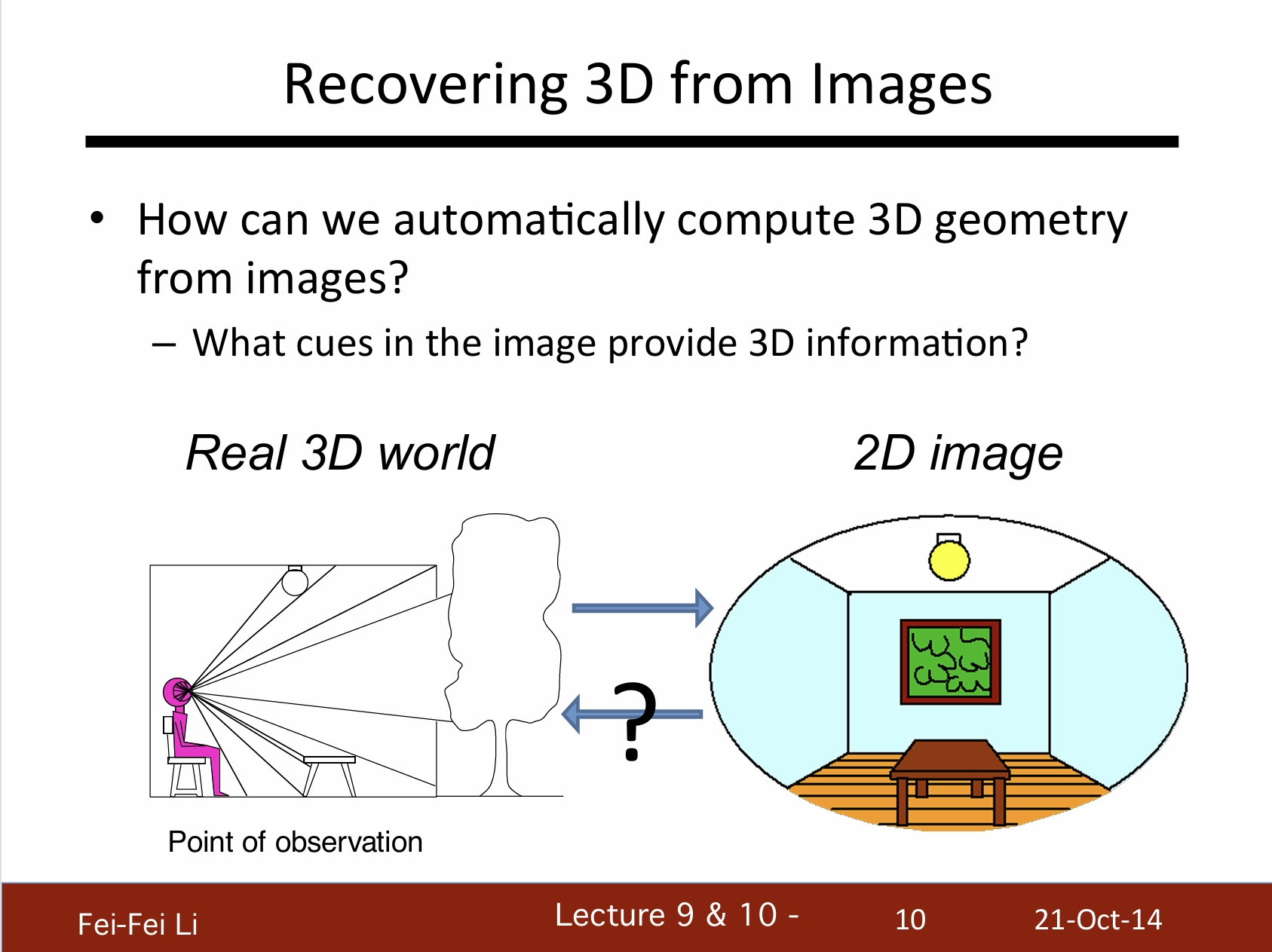
从图像中还原3D
我们如何从图像中计算3D几何信息呢?——哪些图像中的线索能提供3D信息?
明暗
*图中的这个公司Merle Norman Cosmetics是一个换妆品牌子,和主题无关。

纹理
*这里指有一定规律的纹理走向。

焦点

动态

其它:高光、阴影、剪影、内反射、对称型、光学偏振等。
课件中会聚焦在motion这一类线索——追踪图像中某些特征点在不同图像空间的位置。
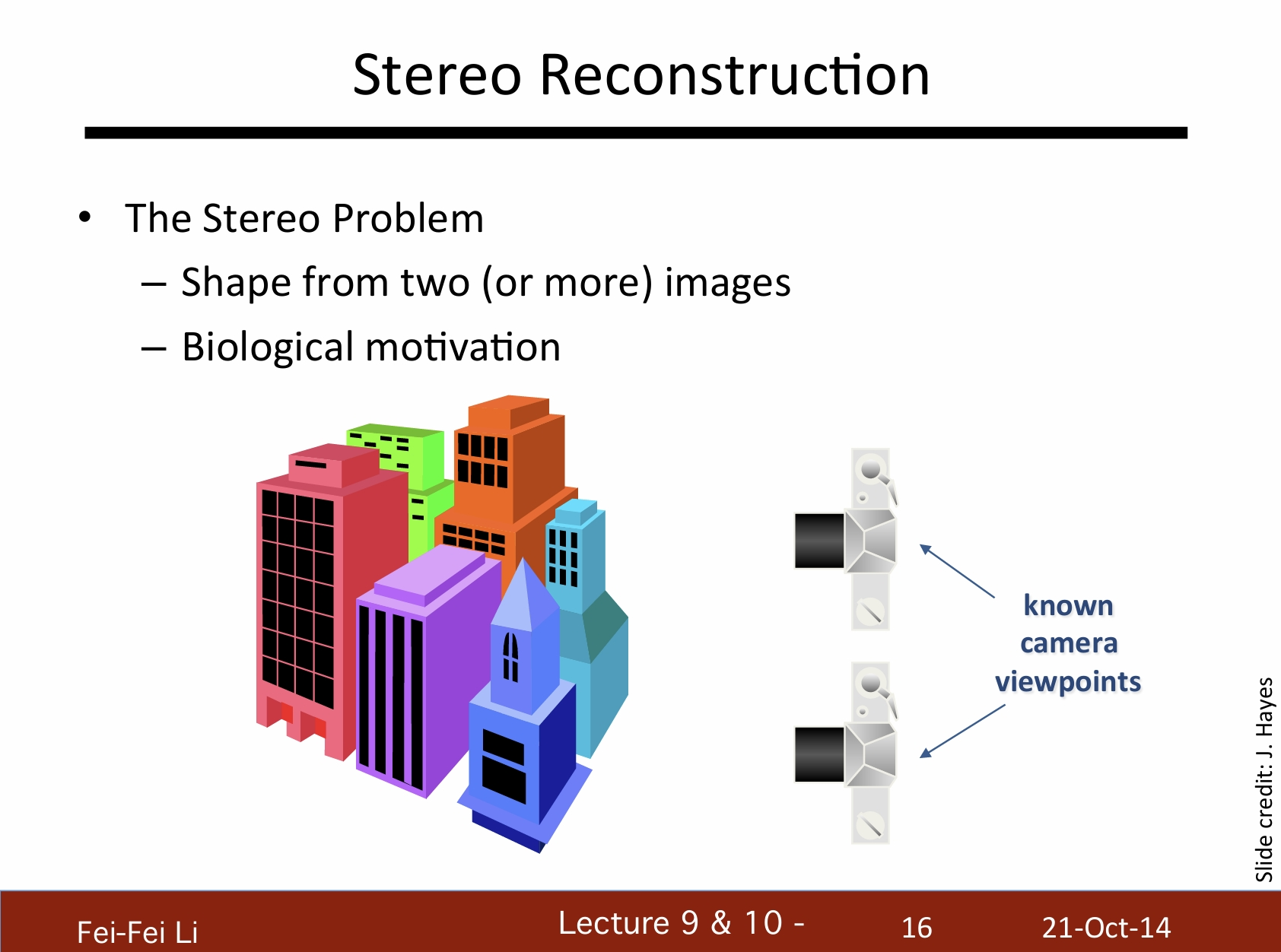
立体重建
立体课题(指为什么要使用多视角):
- 通过两张(或更多)图片生成形体
- 生物性动机(人眼)

1. 二比一更好

2. 从汇聚点还原深度
*基于人眼可以感受双眼夹角的原理,通过图中的公式就可以计算出距离。
三、对极几何的简单引入——Epipolar geometry: a gentle intro
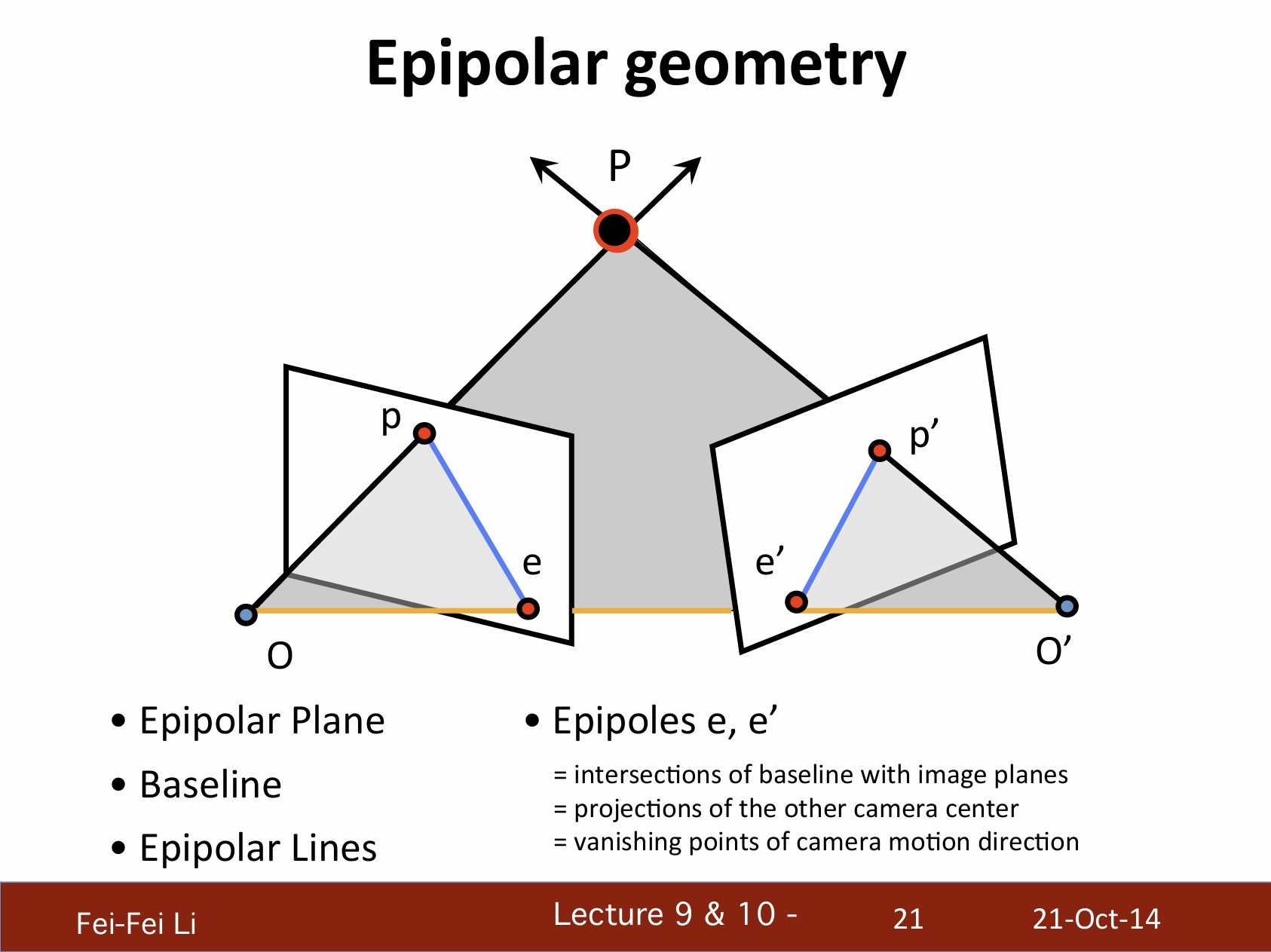
对极几何
*这里引入了几个基本概念:对极平面、基线(黄色)、对极线。
*其中极点e、e'表示:
- 基线和图像平面的交点
- 另一摄像机中心的投影
- 摄像机动态方向的消失点

例子:汇聚图像平面

对极约束
- 同一个物体的不同视角
- 假设已知摄像机的位置和矩阵
- 给定一个左侧图片的点,如何确定右侧图片中该点的位置?
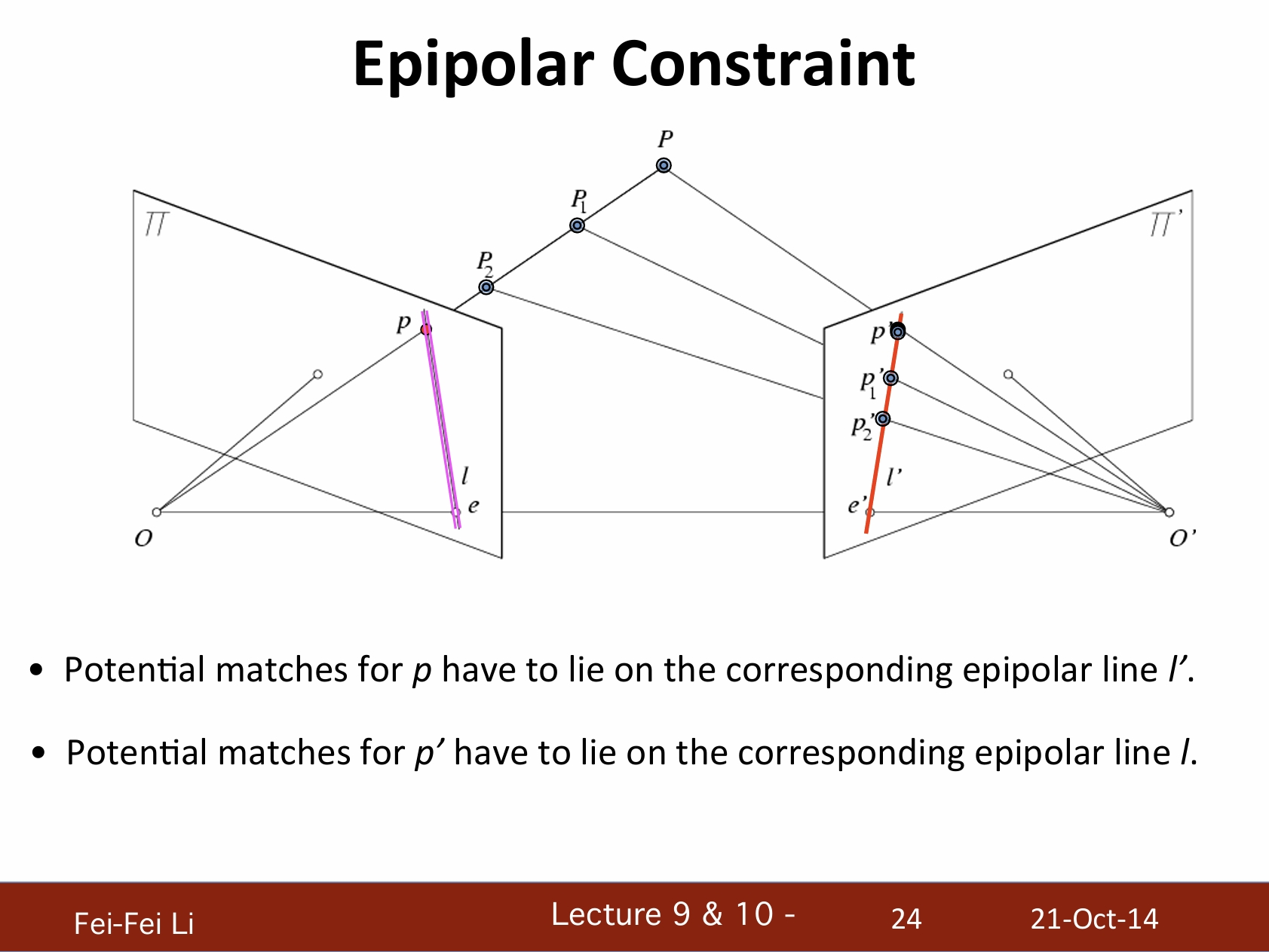
- p点的潜在匹配点必须在对应的极线l'上。
- p'点的潜在匹配点必须在对应的极线l。
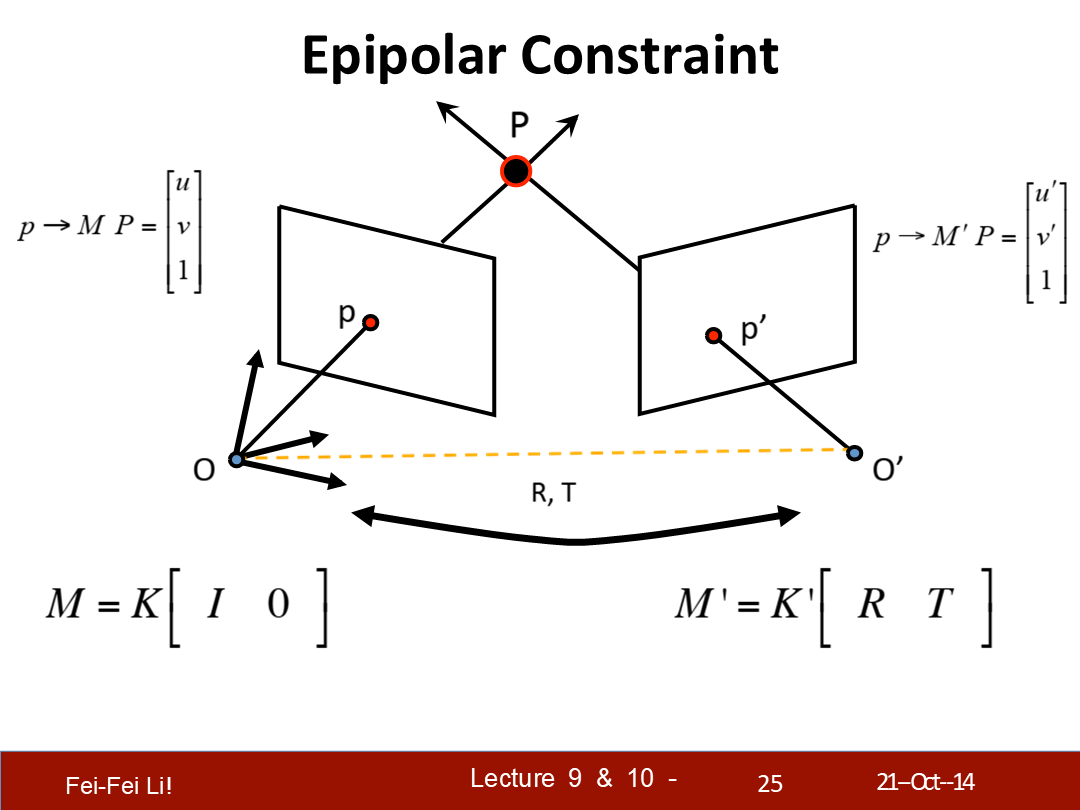
*图中右侧上方应该是p'点,课件应该是写错了。p和p'都是在各自图像平面上投影的点。
*M是左侧摄像机对应的矩阵,写成了之前一节中的形式,K对应之前提到的内部假设,后面的单位阵I是默认旋转矩阵、0则是默认位移矩阵。
*M'则是经过了旋转R和平移T之后的摄像机矩阵。
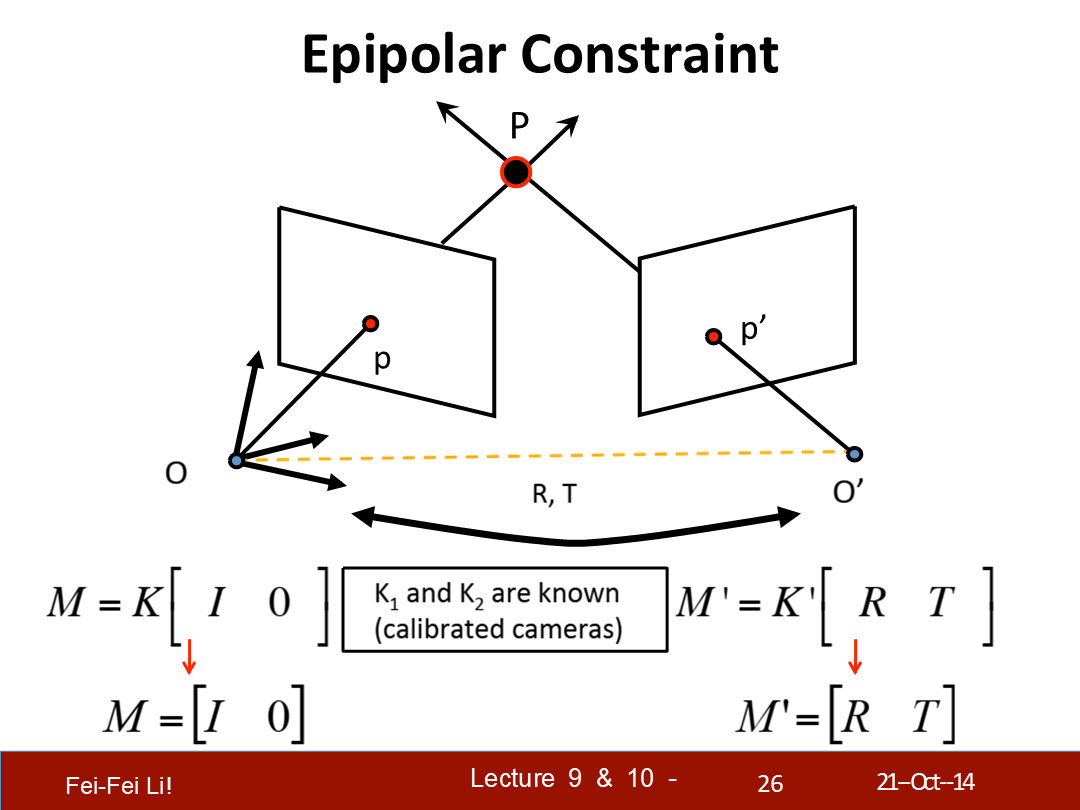
*两者的K值是由校准相机(calibrated camera)的参数来确保的。
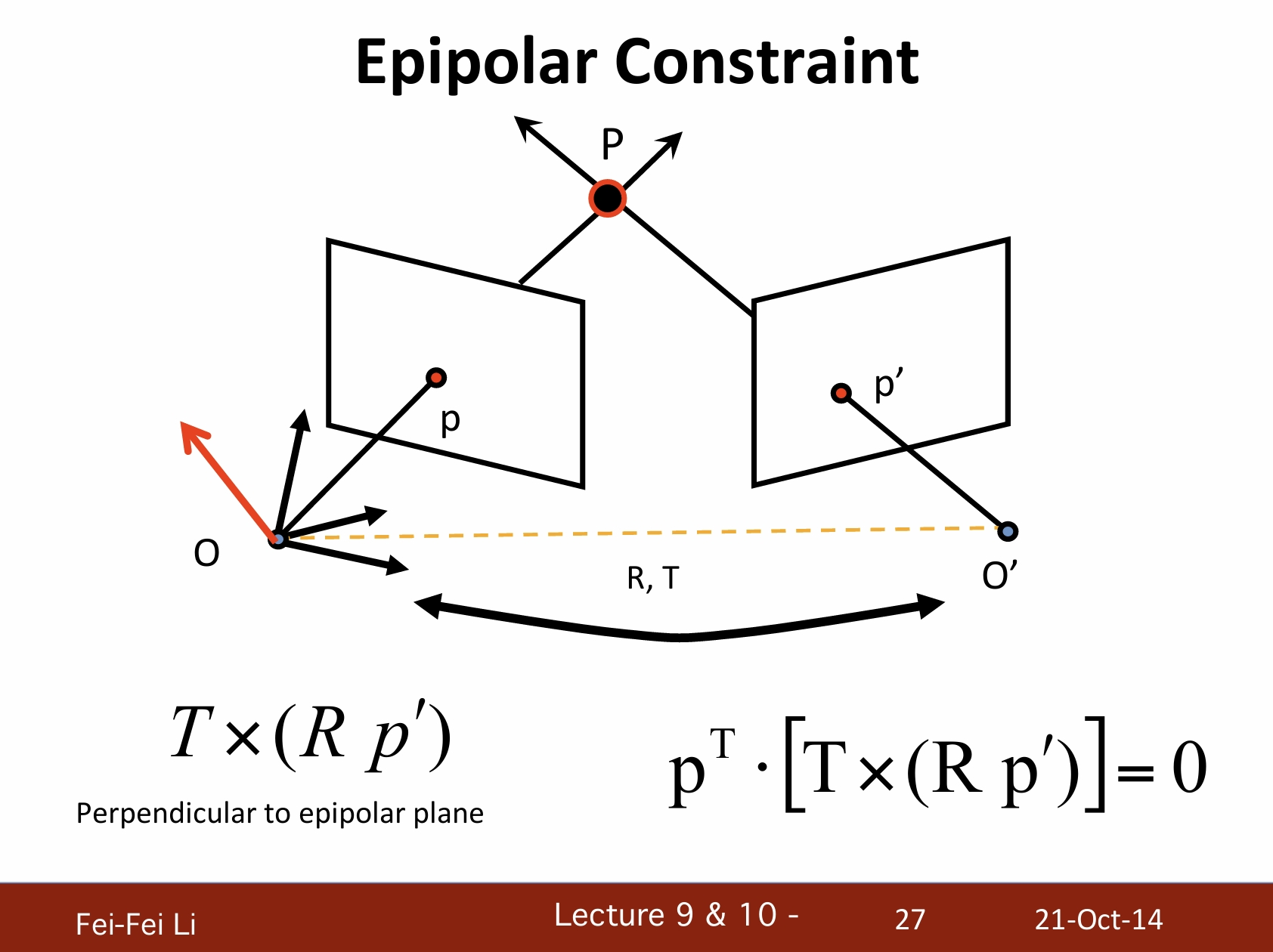
*T叉乘(Rp')得到的向量与对极平面垂直。
*p的转置与之的点乘等于0——代表两者也垂直。矩阵的转置可以理解为将其行列翻转的结果。
*向量点乘得到的是一个标量,而叉乘得到的是一个与两者垂直的法向量。

向量叉乘转为矩阵乘法
*这里引入了一个斜对称矩阵的概念,其对角线上值为0,其它位置的值分布如图。
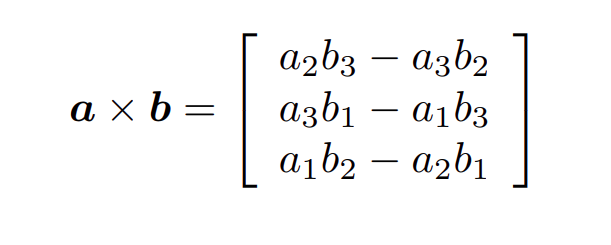
作为参照这里展示了向量叉乘的计算结果
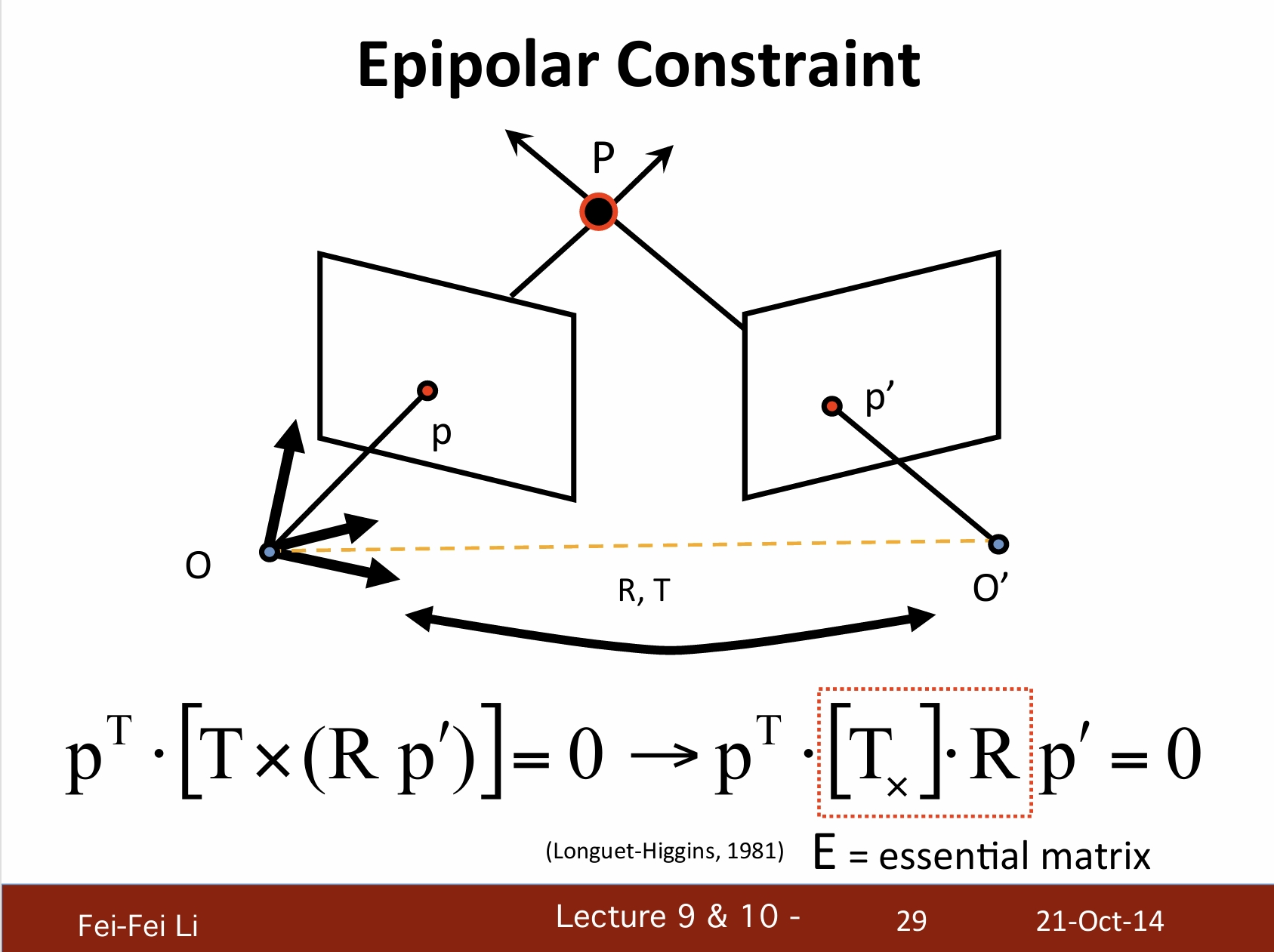
*将之前叉乘的部分转换为矩阵点乘,其中提出的部分被称为本质矩阵。通过它可以快速运算出另一个图像中的极线。
*这一概念于1981年由Higgins提出,这一概念的翻译也在矩阵学中被广泛使用。
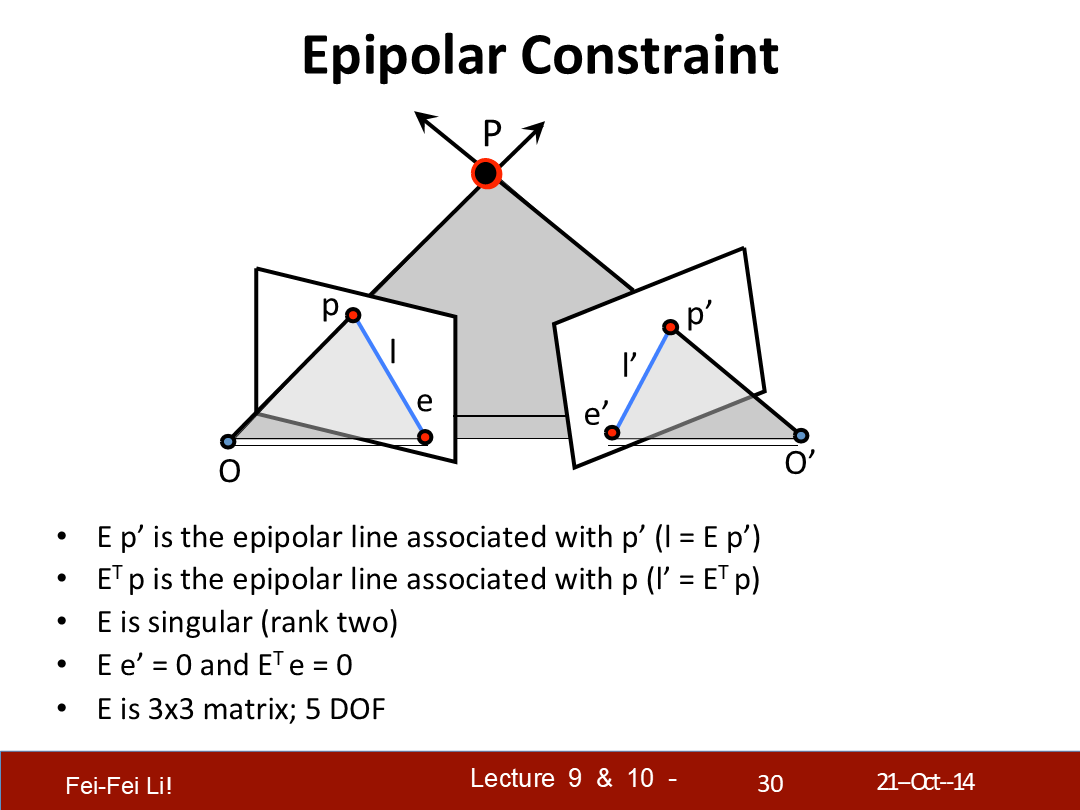
本质矩阵的一些特质如下:
- E乘p'是与p'相关的极限l。
- “E的转置”乘p是与p对应极线p'。
- E是一个奇异矩阵。它没有逆矩阵,并有着EX=0有无限多解的特性。
- E乘e'等于0,E的转置乘e等于0。(这类计算时e和e'视为向量)
- E是一个3X3的矩阵,它有着5的自由度。
*DOF是degree of freedom的缩写,以通俗但不算准确的方式来描述,矩阵自由度值有其中最少多少个参数能确定其约束;又由于对极约束是等式为零的约束,所以对E乘以任意非零常数后,对极约束仍然满足——这件事情称为E在不同尺度下是等价的。 基于平移3个参数、旋转3个参数,尺度等价减1(指其它参数可以按一个参数做等比例缩放),得到自由度为5。
四、平行图片与图像校正——Parallel images & image rectification
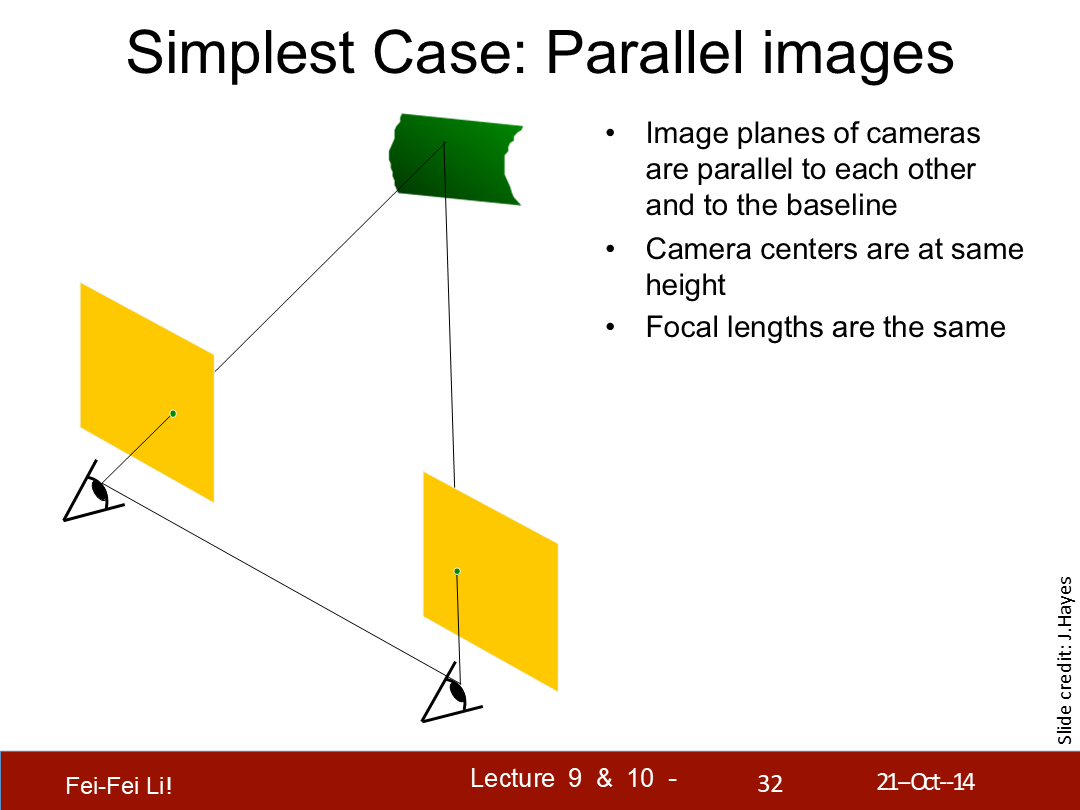
最简单的例子——平行图片
- 摄像机的图像平面彼此平行并与基线平行
- 摄像机中心在同一高度
- 焦距相同
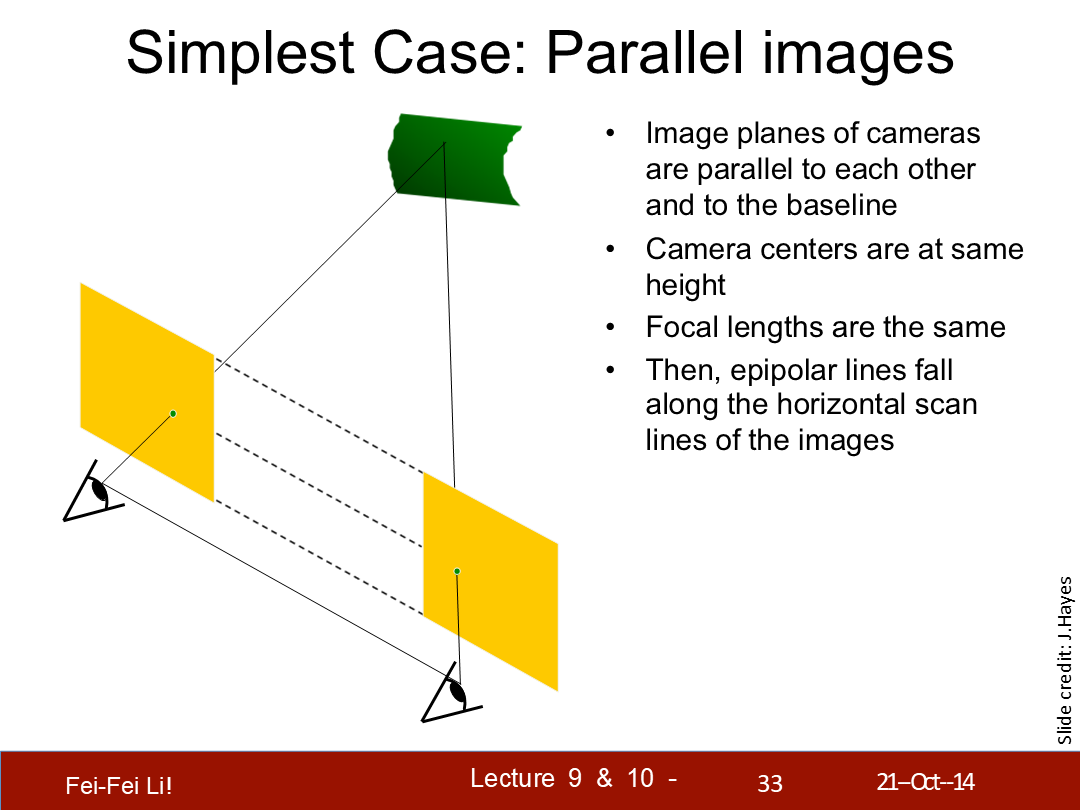
此时,极线就沿着图片的水平扫描线分布。

平行图片的本质矩阵
*这里将t按照之前的规则转换成斜对角矩阵[tx],而R是单位矩阵——这样就得到E。

*由于矩阵乘是有结合律的,因此可以得出v=v'的结论,即图中所说的对应两点的y坐标相同。
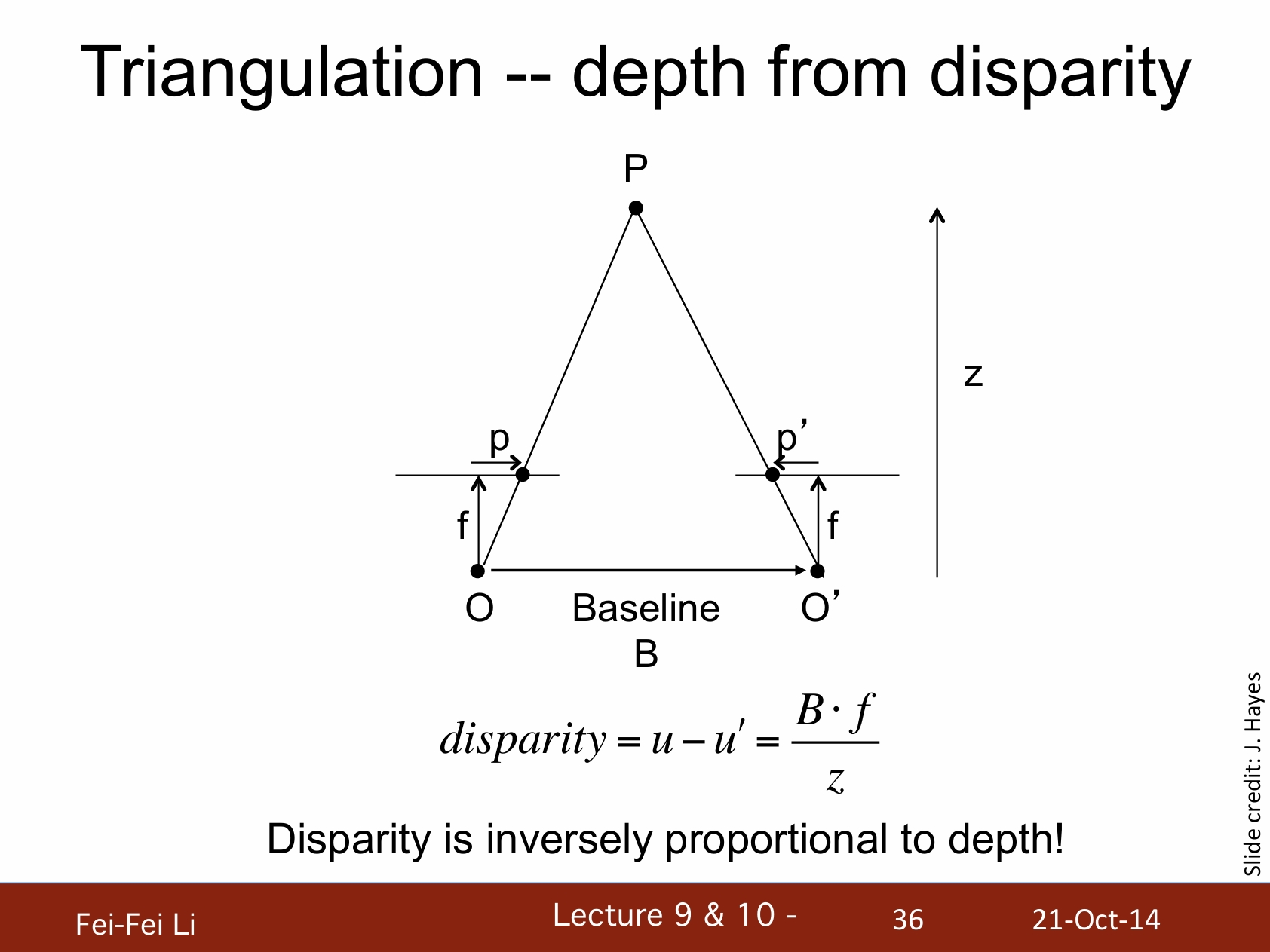
三角测量——依据差异计算深度
*差异(disparity)值是和深度成反比的。
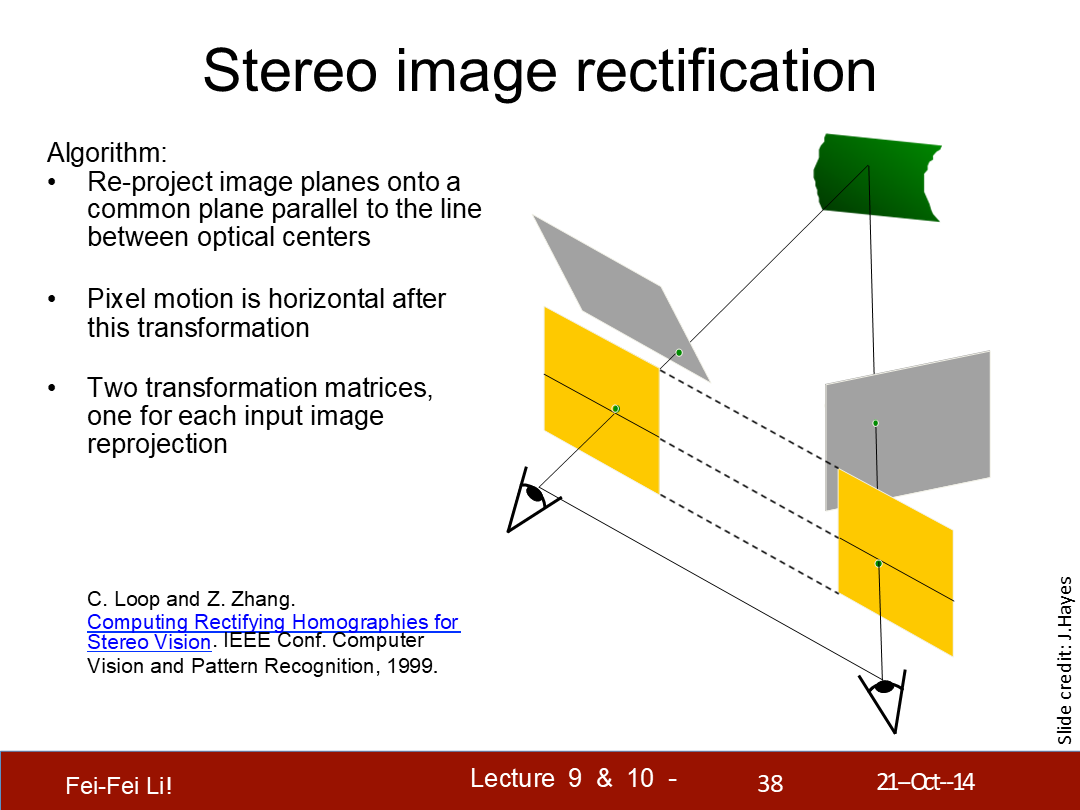
立体图像校正
算法:
- 重投影图像平面,至两个与视觉光学中心线平行的平面上。
- 这次变化之后像素的移动是水平的。
- 两个变换矩阵,对应每个输入图片的投影各一个。
*直译过来稍微有些别扭,但结合示意图理解,实际上是想用多一个步骤的图像平面变换来达到简化计算以及利用三角测量的意义。

校准示例

应用:视觉变形

移除透视扭曲(校正)
结语
由于课件没有解说稿,因此能感觉到有些部分直接上各种公式计算还是缺一点铺垫。而如此高密度的各种矩阵计算,有些我能掌握,也有很多方面我是纯萌新——有些东西只能概念性的把握一下,没法深入再去了解了。
但尽管如此,相信不管是我还是读到这里的各位,应该能从示意图感受到这些计算机视觉领域的前期研究是在处理哪些方面的问题,并为之设计了哪些数学工具和算法的。
尽管只是开了个头,距离读到最前沿和AI都还挺远,但也算是开启了这个读计算机视觉和三维重建方面文章的系列。下周会继续更新这篇课件的下半部分。
最后是一些资料链接:
立体视觉的WIKI
一篇介绍本质矩阵的知乎
一个实用的矩阵计算器工具
介绍摄像机校准的一篇文章
斯坦福大学这篇课件的地址