譯前言:
Puzzle這個概念本身其實不好譯,即使只談作為名詞的puzzle game,在中文裡它也對應到一大堆不同的東西:益智遊戲、智力遊戲、解謎遊戲。也可以指解謎玩具和益智玩具,比如七巧板和華容道。也可以指那些純粹形式的謎題,比如謎語和問題。本文討論的幾個遊戲實例,俄羅斯方塊、Drop7和Orbital,在舊有的中文分類中一般看作是“益智遊戲”(順便一提,這個名稱也側顯了遊戲在中文世界的文化困境,需要“益”智以正名),考慮到探討的嚴肅性和puzzle一詞本身的含義,統一處理為“解謎遊戲”、“解謎”或“謎題”。
譯自 Ian Bogost
How to Talk About Video Games,2015.11
Chapter13 ,pp103-110
松果 / 譯
正文
要討論抽象的解謎遊戲其實很難,特別是探討為什麼某些特定的範例能稱為解謎遊戲的傑作。我們可以討論這些遊戲的形式特性、感官美學、界面;我們可以討論它們的新穎和創新;我們可以討論它們遊玩的挑戰性。但對Drop7或者Orbital這樣的遊戲來說,這樣的觀察似乎只是隔靴搔癢。我們是否能夠用和討論《生化奇兵》(Bioshcok)、《吃豆人》(Pac-man)或者《模擬城市》(Simcity)一樣的方式去討論它們?無論是通過敘事、角色塑造還是模擬,這些遊戲都提供了某種“關於性”(aboutness)。每個遊戲都通過規則和環境,表現一些確鑿的主題。
討論抽象的遊戲,難就難在它們不是確鑿的。有些抽象遊戲有著明顯的實際主題,這給了它們詮釋的切入點。比如,國際象棋,很明顯是從軍事衝突中獲得靈感,不僅是因為它的歷史淵源和作戰的玩法,也因為它的棋子雕刻和命名。當一個騎士吃掉卒子時,很容易就能聯想到作戰的姿態。
而圍棋則有點難以定性。正如哲學家德勒茲和瓜塔裡所說的:“圍棋的棋子,(和象棋)正相反,是小球、是圓盤、是簡單的計數單位,只有一些不具名的、集體的或者是第三人稱的功能:‘它走了一步’。它可以是一個男人、一個女人、一隻蝨子、一頭大象。”儘管人們可以把圍棋的棋子想象成一個士兵、一頭大象甚至一家沃爾瑪,這個遊戲的根本仍然是關於疆域的:誰佔領得多,誰就贏。謎題會帶來更多麻煩。有些邏輯和數學謎題採用了清晰的主題或者故事線,像“三間小屋謎題”。其他像數獨這樣的謎題卻沒有。大多數情況下,謎題在形式上完全是概念性的,表現出的具體性僅僅是一種意外。
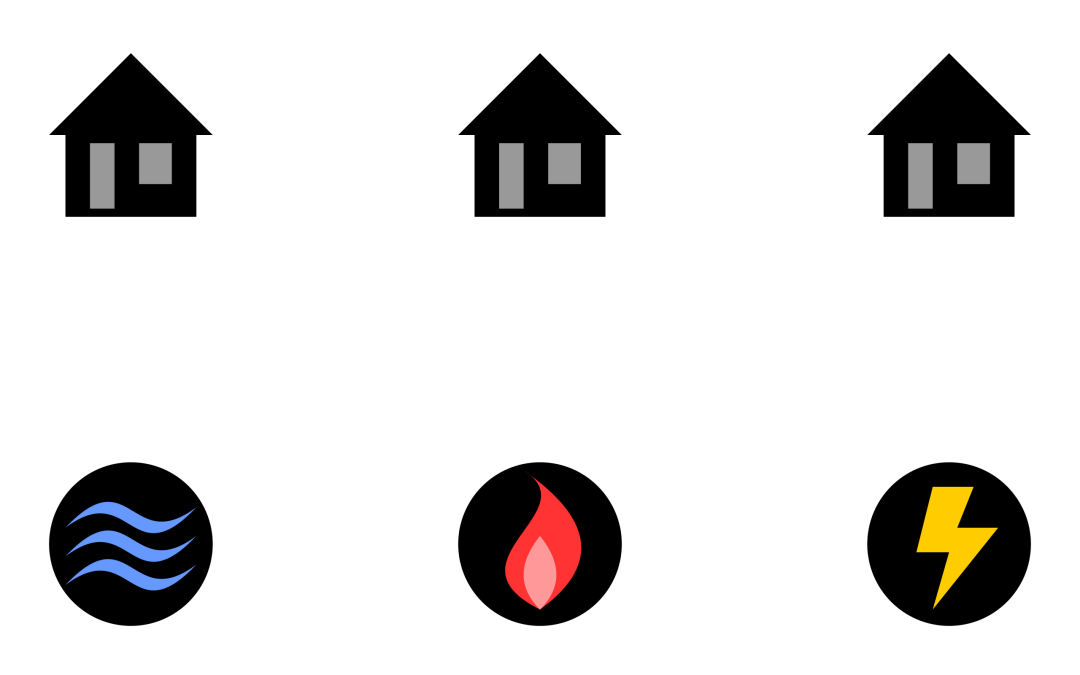
“三間小屋”謎題:假設在平面上(或是在球面上)有三間小屋,要連接到天然氣公司、水廠以及電力公司。若不考慮使用立體架構,也不通過任何小屋或是其他公共設備來傳送資源,是否可以用九條線連結三間小屋及三間公共設備,而且九條線完全沒有交錯?
一盒拼圖遊戲,完成後上面可能會印著一片風景或者一個漢堡,但這個主題和謎題本身並無關係。它只是一個皮膚,用來加速建構拼圖的工作。對於一些可操作的謎題(manipulable puzzles),道理也是如此,比如七巧板。另外一些謎題則是完全抽象的,和世界上的任何存在和行動之間都沒有明顯的關係,比如紙牌接龍和魔方。
電子遊戲從很大程度上繼承瞭解謎的傳統。文字和圖像冒險利用了邏輯謎題,特別是需要操縱物品來開門的謎題。我們也有大量的對傳統的抽象桌遊的改編。不過對當下的抽象遊戲影響最大的,還是可操作的謎題,這有很充分的理由:“空間關係”有很好的可轉化性,而電子遊戲很擅長在空間中操作物體。但是當我們試圖批判性地討論解謎遊戲時,問題就出現了:我們很難對謎題做出縝密的批評,因為謎題傳遞意義的方式並不像小說、電影、繪畫那樣。例如,連鎖商店裡的一副孔明棋(peg solitaire)並不具備宗教文本的功能。
理解抽象藝術的一種方式,是把它們看成隱喻或者寓言。在某些情況下,藝術品的名字有助於我們理解。杜尚的立體主義繪畫《下樓梯的裸女》(Nude Descending a Staircase)迅速揭示了人形在運動中的多視角和疊加。蒙德里安著名的最後一幅作品《百老匯爵士樂》(Broadway Boogie Woogie)也是如此,它抽象地表達了紐約的喧囂。
在別的情況下,作品本身並不能提供這樣的助益,觀者必須尋求自己的闡釋。比如,蒙德里安的《帶黃色塊的構圖》(Composition with Yellow Patch)就是這種情況,繪畫的標題和畫面裡,都沒有解釋的入口。遊戲,也很少通過名稱給我們很多信息,主要是因為遊戲和繪畫史沒有強烈的譜系學關係。然而,如果願意的話,我們的解釋能力還是讓我們能從任何東西里讀出意義來。
對於抽象的解謎遊戲,最著名也最有代表性的解釋是針對最著名的遊戲提出:俄羅斯方塊。Janet Murray在她1997年出版的《全息甲板上的哈姆雷特》(Hamlet on the Holodeck)一書中,將俄羅斯方塊描述為“美國人超負荷生活的完美體現”。方塊骨牌落下,像必須完成的任務、必須閱讀的郵件、必須參加的會議。人們必須迅速行動,否則就會被淹沒。但是檢查完畢、歸檔完畢、或者滿足要求之後,這個過程只會全部重來。沒有安全退出的可能,只有註定的失敗。
評論家Markku Eskelinen質疑Murray的說法十分荒唐:“Murray沒有研究實際上的遊戲,而是試圖解釋它的所謂主題,或者說,是把她偏好的主題投射其上。因此我們沒有學到任何讓俄羅斯方塊得以成為遊戲的特性。”一個蘇聯遊戲竟然被解釋為美國工作倫理的寓言,Eskelinen觀察到了其中的奇異之處,並且提出,“如果有人因為有階級、組織之分的黑白社群之間的持續鬥爭,性別不平等,受困的棋子沒有醫療保險等等,就把國際象棋解釋成一個完美的美國遊戲,那也是同樣離譜至極。”
不過,Murray的闡釋其實是完全合理的。從文學或者藝術批評的角度來看,她提到了一些本質的東西:來自作品本身的根據。遊戲製作於鐵幕之後,這一點其實無足輕重。一部作品可以脫離它的創作語境,和全新的解釋用無數種未曾設想的方式結合,哲學家德里達稱之為“撒播”(dissemination)。沒人能告訴你一件作品的“真正含義”,只要你能從文本中拿出證據來證明你的解釋是合理的。
在討論抽象的解謎遊戲上,Murray和Eskelinen各自方法的問題是:一個希望遊戲只通過某種敘事起作用,另一個希望遊戲只通過形式起作用。但這二者缺一不可。問題似乎是在此:抽象解謎遊戲的“意義”存在於其機制(mechanics)和動態(dynamics)之間的部分,而不是隻存在於其中一個。
哲學家伊曼努爾·康德在18世紀寫就的美學鉅著中,區分了“優美”和“崇高”。他把“美”和對事物形式的非邏輯、主觀的判斷聯繫起來,從想象力和理性之間的關係出發描述“崇高”。
康德描述了兩種類型的崇高。“數學上的崇高”(mathematical sublime)是一種無垠或者浩瀚感,是由無限的“大”產生的反映。金字塔就是這種結構的的例子,它無法一眼窺得全貌;“力學上的崇高”(dynamical sublime)則是一種被壓倒的感覺,它往往來源於自然力量,比如海邊的懸崖或者巨大的雷雲。數學上的崇高產生於巨大,力學上的崇高產生於畏懼。
《Drop7》和《Orbital》這類遊戲的意義,從崇高的層面上理解是最好的,特別是數學上的崇高。
《Drop7》要求玩家將印有1到7的數字的棋子放置到7x7網格的各列中。在重力的作用下,這些數字會下落到底部或者堆積到其他數字上。如果一個棋子上的數字和它所在的行或者列上棋子的數量相同,它就會消失。灰色棋子要在解鎖並顯示出數字後才能消失,想讓灰色棋子解鎖,就要讓與灰色棋子相鄰的棋子消失兩次。每次棋子消失都有分數獎勵,連環combo和清場都有額外獎勵。
《Drop7》中也有很多運氣因素,遊戲開始時盤面上已經有一些棋子。玩家要放置的每個棋子都是隨機抽取的。在某些情況下,出現的是一個恰好需要的數字,讓玩家能夠實行連鎖計劃或者避免危險情況的出現;在別的情況下,一個不需要的棋子會迫使玩家改變計劃。此外,灰色棋子出現時,其內容對玩家來說仍是未知,直到周圍的棋子讓它顯現。總而言之,這些機制要求玩家每回合都重新評估棋盤的狀態。灰色棋子可以被視為不確定因素,但這樣做是不明智的。更好的做法是為最壞情況提前做好準備。

但即便如此,每一局遊戲還是需要根據上一局遊戲的結果和這局的盤面作出全面的重新評估。國際象棋和圍棋中也有突發狀況的存在,但《Drop7》讓每一步行動的長期影響顯示在所有玩家眼前,就算新手玩家也能看清。因此,玩《Drop7》所能得到的體驗是,在一組緩慢變化的確定因素下,針對未來的或然情況做出當下的行動。可能情況的數量只能在一時之間數得過來,但很快就被新信息的隨機性擾亂。這也正是玩家觸及到這個遊戲“數學上的崇高”之處。
對遊戲的掌握總是暫時的,每一步棋都會讓之前的無數可能性崩潰,然後形成一個全新的定局。但不像國際象棋或者圍棋那樣的持續變化,《Drop7》的每一步棋都會在之後揭示出關於自己的更多情況,因為之前屬於未知的影響開始對現狀施加作用。
在《Orbital》中,玩家從界面底部不停旋轉的槍裡發射球體。這些球體在牆面上和彼此之間不停彈射,直到慣性使其停止【譯註:作者此處應該犯了一個錯誤。慣性並不會讓運動的物體停止】。運動一旦停止,球就會開始膨脹,直到它們碰到牆或者另一個球,膨脹才會停止。玩家的目標是通過用新的球撞擊三次來打破這些停止膨脹的球(每個球上的數字顯示了當前的碰撞次數),從而得到一分。然而,如果一個球反彈到了玩家槍口上方的白線以下,遊戲就結束了。為了契合遊戲的宇宙主題,遊戲裡的球體會製造出影響後續球體軌跡的引力場。

像《Drop7》一樣,《Orbital》的玩家也必須面對一個取決於不斷增加的偶然性的遊戲環境。遊戲的策略之一是根據環境的摩擦力和引力去估算小球的軌跡。比如,玩家可以試著把球體聚集在角落裡,這樣也許一次發射就能摧毀許多球體。但是隨著球體位置的確定,它們又會改變一部分遊戲區域裡的引力,這有效地抹去了玩家對於早期結構的理解。值得注意的是,就算玩家成功了,這種迷茫還是會出現,因為小球的爆炸同樣會改變區域內的重力。
在《Drop7》裡,數學上的崇高通過或然性進入遊戲,即兩種棋子的隨機生成。在《Orbital》裡,無論如何都沒有任何的或然性,遊戲裡的所有運動都是可計算的,但是宇宙的變動不居讓人類玩家無法做到這一點。玩家的每次射擊都必須同時把握時機和物理,不論這次操作是不是預料之內的。《Orbital》是苛刻的,它把那條代表失敗、輕觸即潰的細線擺在屏幕上,《Drop7》則是慢慢地削減選擇,直到失敗來臨。
玩《Drop7》和《Orbital》就像在推演弦理論,在評估無限未來的未知可能。不論一個人玩得好不好,這些遊戲都迫使玩家審視系統——那個驅動遊戲的系統、那個每一步都自我更新的系統——在數學上的無垠。
我們能說《Drop7》和《Orbital》這樣的遊戲是“關於”什麼的嗎?如果可以,又到底是“什麼”?這時就有必要回到Murray對俄羅斯方塊的闡釋,畢竟人們可能會在俄羅斯方塊的遊玩中體會到類似的數學崇高。每個方塊都會改變遊戲的結構,玩家必須變換結構才能繼續遊戲,而幾率決定了哪些形狀能夠被用來填補之前留下的幾何空缺。《Drop7》和《Orbital》與之不同的重要一點是:它們是回合制的,而不是連續的。玩家必須參與其中來進行下一步動作,這是一個反思艱鉅任務的機會,也是一種來自崇高的要求。
當Murray將俄羅斯方塊視作一個關於工作的西西弗寓言時,她不是在說遊戲有數學上的崇高的動態性,而是遊戲操作的時間動態性。而“時間”,恰好是Eskelinen在反駁了Murray的敘事主義之後提出的正式解釋。辦公事務【譯註:這裡指俄羅斯方塊所需要的、近乎工作的反覆勞動】並不像《Drop7》和《Orbital》那樣崇高,能快速產生分叉的平行世界,但它往往是一種對時間之箭的體驗,對無法阻擋的過程的體驗,無論是否取得結果。
在俄羅斯方塊中,遊玩的方式阻礙了我們通往崇高。但是在《Drop7》《Orbital》和中,玩家對崇高的沉思和反應卻因為回合制的行動模式得到加強。每一步之間的停頓,都可能讓感覺更富寓意,並將其視為遊戲的主題。比如說,《Drop7》帶來了一種體驗:面對不可知的恐懼和渺小——不僅僅是對未來(等待放置的棋子)的不可知,而且是對過去(灰色棋子)的不可知。這種體驗感覺很像,比如說,個人選擇——一個人該向紅十字會捐款嗎?該皈依伊斯蘭教嗎?該找個情人嗎?
要說清楚的是,《Drop7》的表層設計和模型實際完全沒有這種感覺,但是這種關於數學上的崇高的經驗在兩個案例裡都是相似的。從這方面,也許會有人說《Drop7》比《神鬼寓言》(Fable)和《生化奇兵》更加註重道德選擇。雖然後兩者可能模擬出了“決定”這一行為,但就像俄羅斯方塊和“工作”的關係一樣,他們沒有更加動態地去貼近“選擇”的主題。
《Orbital》建立在這一主題之上,但走向了完全不同的方向。在排除了隨機性後,Orbital的主題圍繞著“放置”(placement)展開。即便擁有關於宇宙物理的全部動力學知識(這個主題合適地寄身於遊戲的視覺呈現),人類玩家在經過一定時間後還是太過容易犯錯。就算是高手也會有欠缺。對此類遊戲的這種闡釋,也只是眾多闡釋中的一種,它們不會產生於遊戲的機制,或者機制運行產生的動態過程中。相反地,它們形成於玩家在這二者之間寓言般地竭力感知的過程。
好的解謎遊戲可以做很多事。但是根據成癮性、深度、優雅性這樣的特性——這是評判俄羅斯方塊、《Drop7》或者《Orbital》這些遊戲的常見價值維度——認為這些遊戲是“好”的,就等於是在說抽象遊戲只能對玩家施加冷血的、形式上的影響。而崇高,正是冷酷的形式主義的對立面:一種壓倒性的、廣闊和豐沛的感覺。崇高讓我們看到自身理性的侷限,向我們展示世界的變動和浩瀚。當然,這樣的主題並不能被區區幾個磚塊、數字和形狀的遊戲窮盡,就像它也無法被區區幾個關於戰爭、犧牲和失去的遊戲把握一樣。解謎遊戲在數學上的崇高,就是要讓我們拋開作為造物者和批評者的目標。我們通過把遊戲和電影、繪畫、文學這些熟悉的表現性藝術作比較,去發現什麼是遊戲的“傑作”。但是崇高也在別處:在建築裡,在自然裡、在天氣裡。或許,我們也應從這些地方尋求啟發。