這個盒友又在刷小黑盒了,與其把空閒時間用來刷盒,不如多多學習提升自我,來看一道簡單的小學數學題吧!
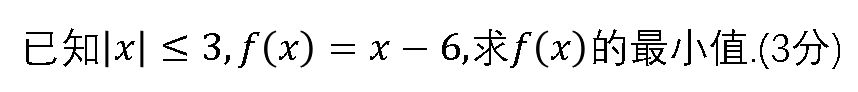
簡單的小學數學題
聰明的盒友一眼就看出來了,答案是-9!
很明顯這是一道帶約束的求函數最小值的問題,那麼把問題稍微拓展一下,我們來看一道類似的題目吧!
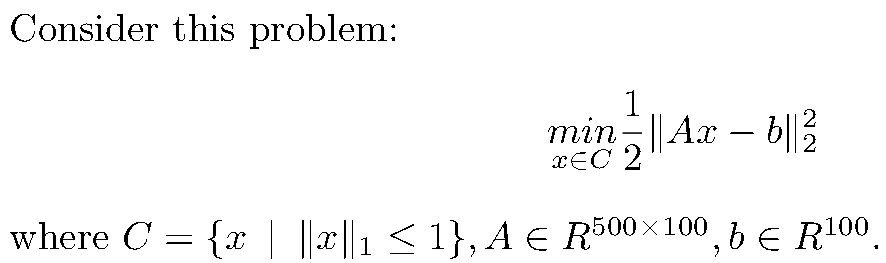
類似簡單的小學數學題的問題
可以看到,這同樣是帶約束的函數最小值求解問題,但是規定了自變量向量x的L1範數的上界,同時係數的維度過大,讓問題變得稍微有一點難。不過不要擔心,讓作者帶領盒友解決這個問題。
導數與梯度下降法
眾所周知,求解函數最小值可以用求導數的方法解決。如果函數是凸的(Convex),會有最小值點的一階導數(First-order gradient)會等於零,同時二階導數(Second-order gradient)會大於零。那麼讓我們先拋開事實(約束)不談,對函數進行求導。很容易得到函數的導數如下:
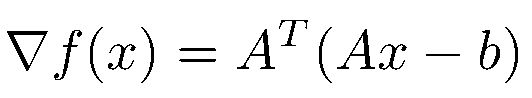
一階導數
在這裡我們假設二階導數總是大於零的,不考慮二階導數的問題,這涉及到逃離鞍點(escape saddle point)問題。
接著我們只要令一階導數為全零向量,就能求得函數的全局最小值。但是求解析解需要計算逆矩陣,這導致了O(n^3)的時間複雜度,即使一些改進的算法也只能夠逼近O(n^2.81)的時間複雜度,這與向量維度成多項式比,是我們不可接受的。而很多時候我們不需要非常精確的結果,只要求一個近似值,因此我們可以採用梯度下降法(Gradient descent)來對x進行逼近:
梯度下降法的迭代公式
其中t是步長(step size)。
近端梯度法與投影
但是不要忘了,我們還有約束限制,而任何一步梯度下降可能會導致原先在約束下的變量迭代為不滿足約束的變量,在幾何意義上就是點跳出了集合代表的封閉空間。
因此我們考慮這樣一種方法:每經過一次梯度迭代,我們求一個既最小化約束項、又距離迭代後的點足夠近的點。這種方法稱為近端梯度法(Proximal gradient method,PGD),其核心在於求上述這個被稱為近端算子(prox-operator)或者近端映射(proximal mapping)的點。其公式如下:
prox-operator
其中h(u)是約束項。
但上述方法沒有明確的定義域限制,即可以接受x不在定義域之中,這是我們的設定有所區別。因此我們將約束項h(x)看作是x的指示函數(indicator function),即相當於將約束項的懲罰變為無窮大,其定義如下:
indicator function
那麼近端算子的公式就變為了
prox-operator
這個式子在幾何意義上,就是將x投影到集合C所代表的封閉空間上。
回到問題,我們的約束是x的L1範數的上界,也就是說我們要把一個點投影到L1範數球(norm ball)上。以三維空間舉例,就是把點投影到下圖中的那個八面體上。
一個有名的範數幾何圖
但是我們的維度足足有100,如何正確地把點進行投影就是我們接下來要解決的問題。
L1範數球投影
在上一節中,我們得到了帶指示函數的近端算子,從原理上來講,近端算子所求的點就是投影之後的點。那麼經過簡單地數學計算,我們有:
soft-thresholding
其中k表示向量x的第k個分量,這一步也稱軟閾值(Soft-Thresholding)算子。而lambda受下列等式約束:
然後我們只要求得lambda的解析解,就能得到任意x的近端算子了;得到近端算子,就能對梯度迭代後的點進行投影了;重複梯度迭代、投影,就能求得約束限制下最小化目標函數的近似解了。
這個解析解作者剛開始還不會求,幸好有盒友相助,在這裡要感謝盒友的智慧。
總之,lambda的解析解如下:將x的分量的絕對值從小到大排列:
lambda
這樣就能輕鬆愉快地求解原函數在約束下的最小值啦!
最後,針對隨機高斯分佈的矩陣A和向量b,利用這種方法求解函數最小值的過程曲線如下:
PGD
參考文獻:
Gradient Methods for Minimizing Composite Objective Function
Optimization Methods for Large-Scale Systems
A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems
A Proximal Stochastic Gradient Method with Progressive Variance Reduction