这个盒友又在刷小黑盒了,与其把空闲时间用来刷盒,不如多多学习提升自我,来看一道简单的小学数学题吧!
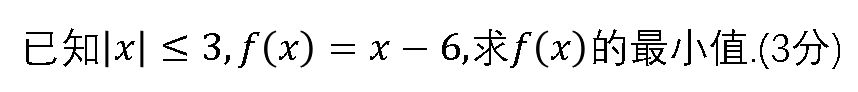
简单的小学数学题
聪明的盒友一眼就看出来了,答案是-9!
很明显这是一道带约束的求函数最小值的问题,那么把问题稍微拓展一下,我们来看一道类似的题目吧!
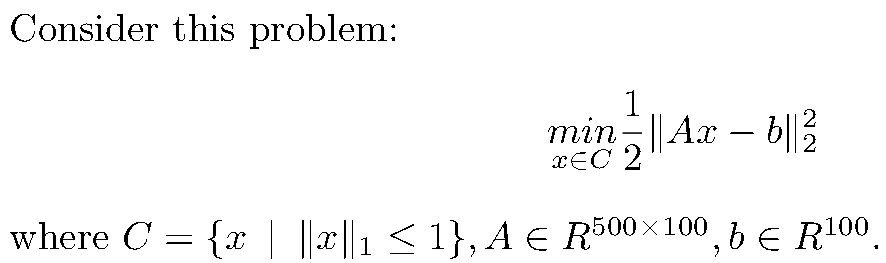
类似简单的小学数学题的问题
可以看到,这同样是带约束的函数最小值求解问题,但是规定了自变量向量x的L1范数的上界,同时系数的维度过大,让问题变得稍微有一点难。不过不要担心,让作者带领盒友解决这个问题。
导数与梯度下降法
众所周知,求解函数最小值可以用求导数的方法解决。如果函数是凸的(Convex),会有最小值点的一阶导数(First-order gradient)会等于零,同时二阶导数(Second-order gradient)会大于零。那么让我们先抛开事实(约束)不谈,对函数进行求导。很容易得到函数的导数如下:
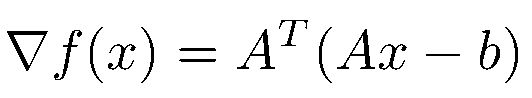
一阶导数
在这里我们假设二阶导数总是大于零的,不考虑二阶导数的问题,这涉及到逃离鞍点(escape saddle point)问题。
接着我们只要令一阶导数为全零向量,就能求得函数的全局最小值。但是求解析解需要计算逆矩阵,这导致了O(n^3)的时间复杂度,即使一些改进的算法也只能够逼近O(n^2.81)的时间复杂度,这与向量维度成多项式比,是我们不可接受的。而很多时候我们不需要非常精确的结果,只要求一个近似值,因此我们可以采用梯度下降法(Gradient descent)来对x进行逼近:
梯度下降法的迭代公式
其中t是步长(step size)。
近端梯度法与投影
但是不要忘了,我们还有约束限制,而任何一步梯度下降可能会导致原先在约束下的变量迭代为不满足约束的变量,在几何意义上就是点跳出了集合代表的封闭空间。
因此我们考虑这样一种方法:每经过一次梯度迭代,我们求一个既最小化约束项、又距离迭代后的点足够近的点。这种方法称为近端梯度法(Proximal gradient method,PGD),其核心在于求上述这个被称为近端算子(prox-operator)或者近端映射(proximal mapping)的点。其公式如下:
prox-operator
其中h(u)是约束项。
但上述方法没有明确的定义域限制,即可以接受x不在定义域之中,这是我们的设定有所区别。因此我们将约束项h(x)看作是x的指示函数(indicator function),即相当于将约束项的惩罚变为无穷大,其定义如下:
indicator function
那么近端算子的公式就变为了
prox-operator
这个式子在几何意义上,就是将x投影到集合C所代表的封闭空间上。
回到问题,我们的约束是x的L1范数的上界,也就是说我们要把一个点投影到L1范数球(norm ball)上。以三维空间举例,就是把点投影到下图中的那个八面体上。
一个有名的范数几何图
但是我们的维度足足有100,如何正确地把点进行投影就是我们接下来要解决的问题。
L1范数球投影
在上一节中,我们得到了带指示函数的近端算子,从原理上来讲,近端算子所求的点就是投影之后的点。那么经过简单地数学计算,我们有:
soft-thresholding
其中k表示向量x的第k个分量,这一步也称软阈值(Soft-Thresholding)算子。而lambda受下列等式约束:
然后我们只要求得lambda的解析解,就能得到任意x的近端算子了;得到近端算子,就能对梯度迭代后的点进行投影了;重复梯度迭代、投影,就能求得约束限制下最小化目标函数的近似解了。
这个解析解作者刚开始还不会求,幸好有盒友相助,在这里要感谢盒友的智慧。
总之,lambda的解析解如下:将x的分量的绝对值从小到大排列:
lambda
这样就能轻松愉快地求解原函数在约束下的最小值啦!
最后,针对随机高斯分布的矩阵A和向量b,利用这种方法求解函数最小值的过程曲线如下:
PGD
参考文献:
Gradient Methods for Minimizing Composite Objective Function
Optimization Methods for Large-Scale Systems
A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems
A Proximal Stochastic Gradient Method with Progressive Variance Reduction