在動筆寫這篇文章之前,我其實猶豫了挺久。
作為一個經驗並不豐富的設計師,我不能確定在三週的期限內,自己是否真的製作出了一款“好玩的”策略遊戲,也不知道是否配得上站在“設計師”的視角,寫一篇這樣的分析文章。
不過在最後,我還是決定斗膽把這篇文章寫完發出來。我想其中應該有不少錯誤之處,也更有許多自以為是的見解。希望這能作為一個例子,供大家分析和批判吧。
很歡迎大家與我討論!
一 冒險決策與穩妥決策
Games are a series of interesting decisions. 遊戲是一系列有趣的決策。 ——席德 · 梅爾
這裡,我想暫時拋開本次設計的遊戲不談,先聊一聊“有趣的決策”:如果有兩個選項A和B擺在面前,如何讓做出抉擇的過程變得“有趣”呢?
我認為,一個決策之所以會“有趣”,其中至少需要包含兩個要素:
首先,兩個選擇不應該有明顯的優劣之分,一個選擇不應在絕大多數場合下都優於另一個選擇。當然,這不意味著在當下的場合,選項之間真的沒有優劣,可能在某些情況下,選項A更為合適,但在另一些情況下選項B更為合適。但這個過程不應該是顯然的,而是需要進行一些思考與評估。例如,在玩一款Roguelike DBG遊戲的時候,你可能會在“獲得10點格擋”與“造成10點傷害”的兩張卡牌之間做出有意義的選擇——這取決於卡組中目前的攻擊牌與防禦牌的比例、質量、特殊效果,甚至你期望的打法等。雖然一個非常熟練的玩家在觀看時,可能會認為在當前場合選擇前者會明顯更優,但是對做出決定的玩家而言,這卻是實實在在的、通過思考和評估做出的抉擇。但是,如果是“造成10點傷害”與“造成8點傷害”之間的抉擇,就會變得毫無意義——如果不考慮遊戲本身的特殊機制,前者顯然是要比後者好的,無論是在什麼卡組中。
其次,兩個選擇需要導向不同的遊戲體驗。這個遊戲體驗是廣義的,包括而不限於數值體驗、構築的流派、緊張程度,甚至可以是視聽效果、劇情體驗。舉幾個例子:在Battle Royale類遊戲中,還剩下10個人、即將縮圈時,是選擇冒著巨大風險率先進圈佔據有利位置,還是選擇先找個安全的地方等待,在最後時刻再嘗試向內圈移動,在此刻就會導向完全不同的緊張程度和對戰體驗。在Roguelike DBG遊戲中,在前期選擇拿一張很難打出combo但一旦成型就非常厲害的牌,還是選擇拿一張無論何時都能穩定取得少量收益的牌,會直接影響這局的構築思路和遊戲體驗。
在一款策略遊戲中,如何用最簡單的方法構造出一個有趣的選擇呢?
我認為,應該是引入一個“冒險決策”和一個“穩妥決策”,例如:
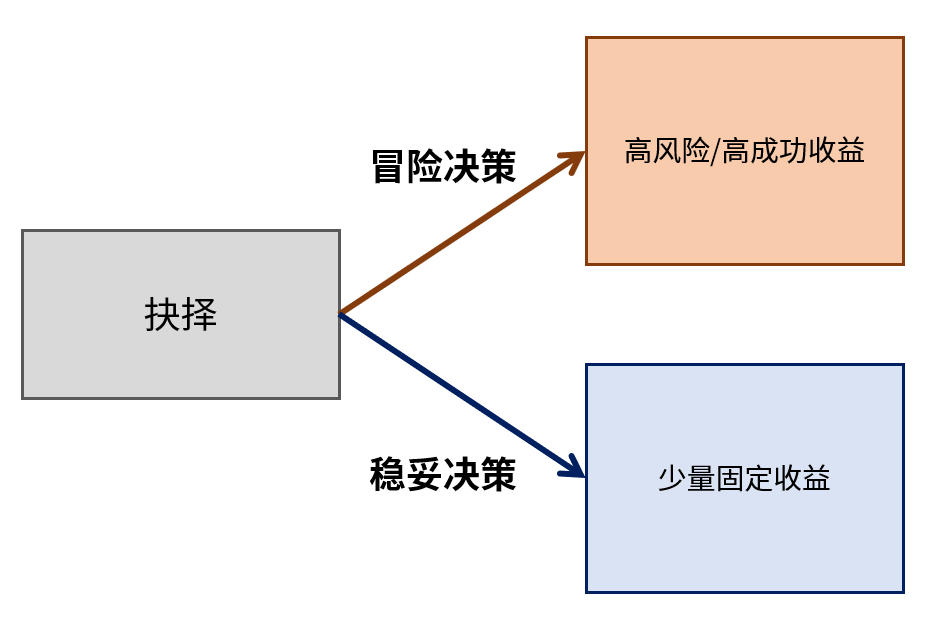
冒險決策與穩妥決策的選擇
這是最常見的有意義決策:選擇高收益、高風險,或是選擇一個固定的較低收益。
在這裡,我嘗試用一個特定的視角,進一步分析上面兩個決策的數學意義。當然,這只是一種基於個人觀點的片面解讀方法。雖然《豐饒女神之骰》的部分設計使用了這種思路,但這個分析框架本身未必正確,也顯然也不能用於總結所有的決策設計,僅作為一種解讀思路參考:
- 高風險、高收益,一般意味著收益的上限被提高,而下限無法提高(有時候反而會降低)。這不一定意味著你的收益期望會提高,但一定意味著收益的方差被提高。
- 固定的較低收益,一般意味著收益的下限被提高,而上限不會有明顯的變化。這意味著你的收益的方差被降低。
也就是說,如果採用了這種解讀方式,我們可以將兩種決策用更加數學化的方式表達出來:
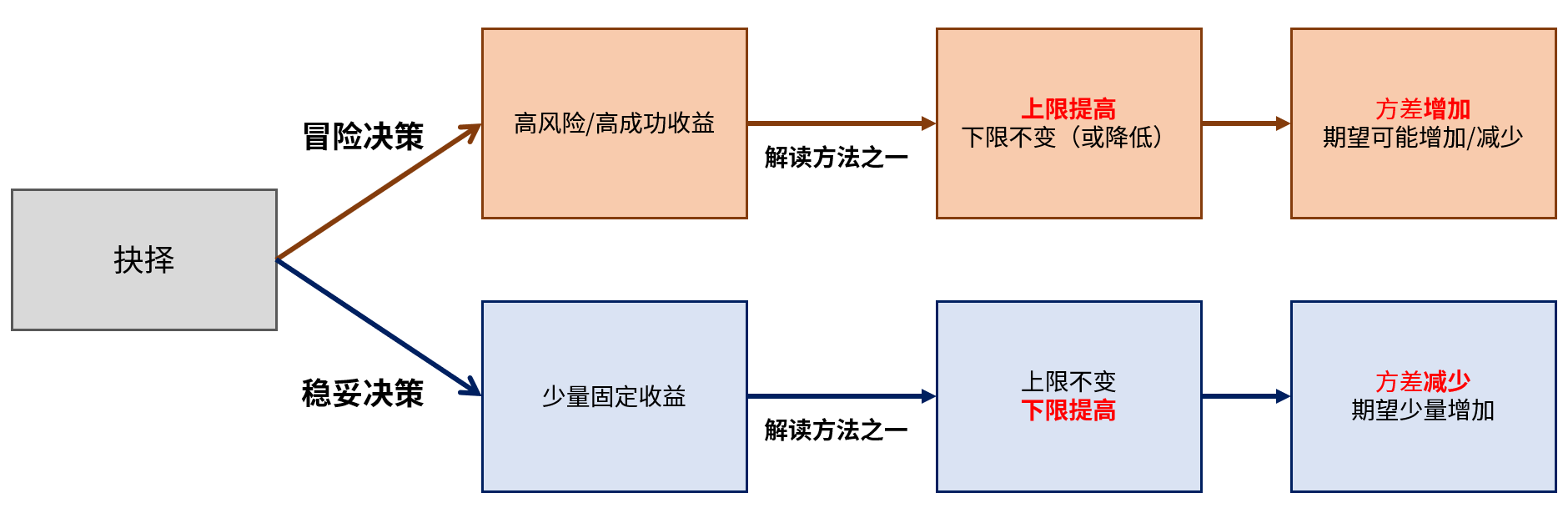
用方差和上下限的視角來看待兩種決策的區別
具體到一局遊戲中,期望往往代表了你的宏觀“勝率”,也就是這個決策“好不好”。而方差往往代表了這局遊戲中的體驗差別:是緊張地等待神抽,還是穩妥地等待勝利。
而兩類決策的主要區別,也不是取決於“期望”,而是取決於“方差”的增減。
雖然可能不太精確,但我們可以試著將每個決策中包含的“冒險決策”與“穩妥決策”成分畫到一個二維座標系上。其中X軸代表了一個決策的“穩妥性”,換句話說是,這個決策增加收益下限的能力。而Y軸代表了一個決策的“冒險性”,也就是這個決策增加收益上限的能力。
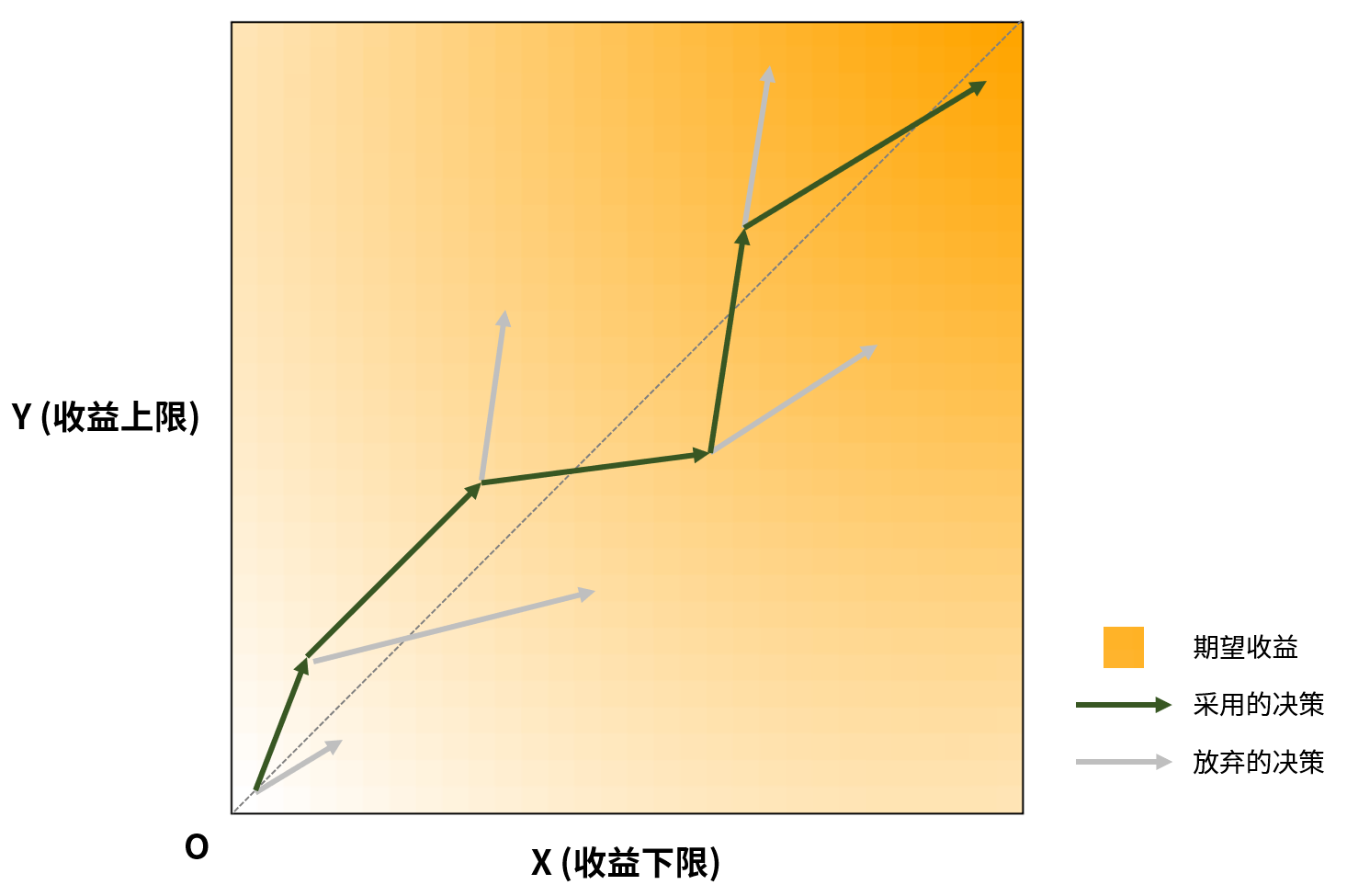
一局虛構Roguelike遊戲中,玩家做出的幾次關鍵決策,其中深色箭頭的連線代表玩家的幾次抉擇所定義出的“決策路徑”。越靠近左上角,代表玩家此時的狀態越“冒險”,越靠近右下角,代表玩家此時的狀態越“穩妥”
如圖所示,這張圖定性地(非定量地)描述了某局虛構Roguelike遊戲中玩家做出的幾次關鍵抉擇。
一般而言,如果遊戲有比較強的策略性,那麼玩家需要控制選擇“冒險決策”和“穩妥決策”的比例。當兩者的比例比較均衡時,通常能夠獲得最高的收益。反之,如果選擇兩種決策的比例過於懸殊,則會陷入困境(過於冒進/過於保守往往會導致一些懲罰)。而具體到每一次的收益大小,就需要審時度勢地結合各種因素進行考慮。
這在圖中體現在,沿著虛線方向前進一般會獲得最高的收益,但每次玩家面對的兩個箭頭,則可能有不同的方向與長度(卡牌或裝備是否強力/是否適合當前build)。
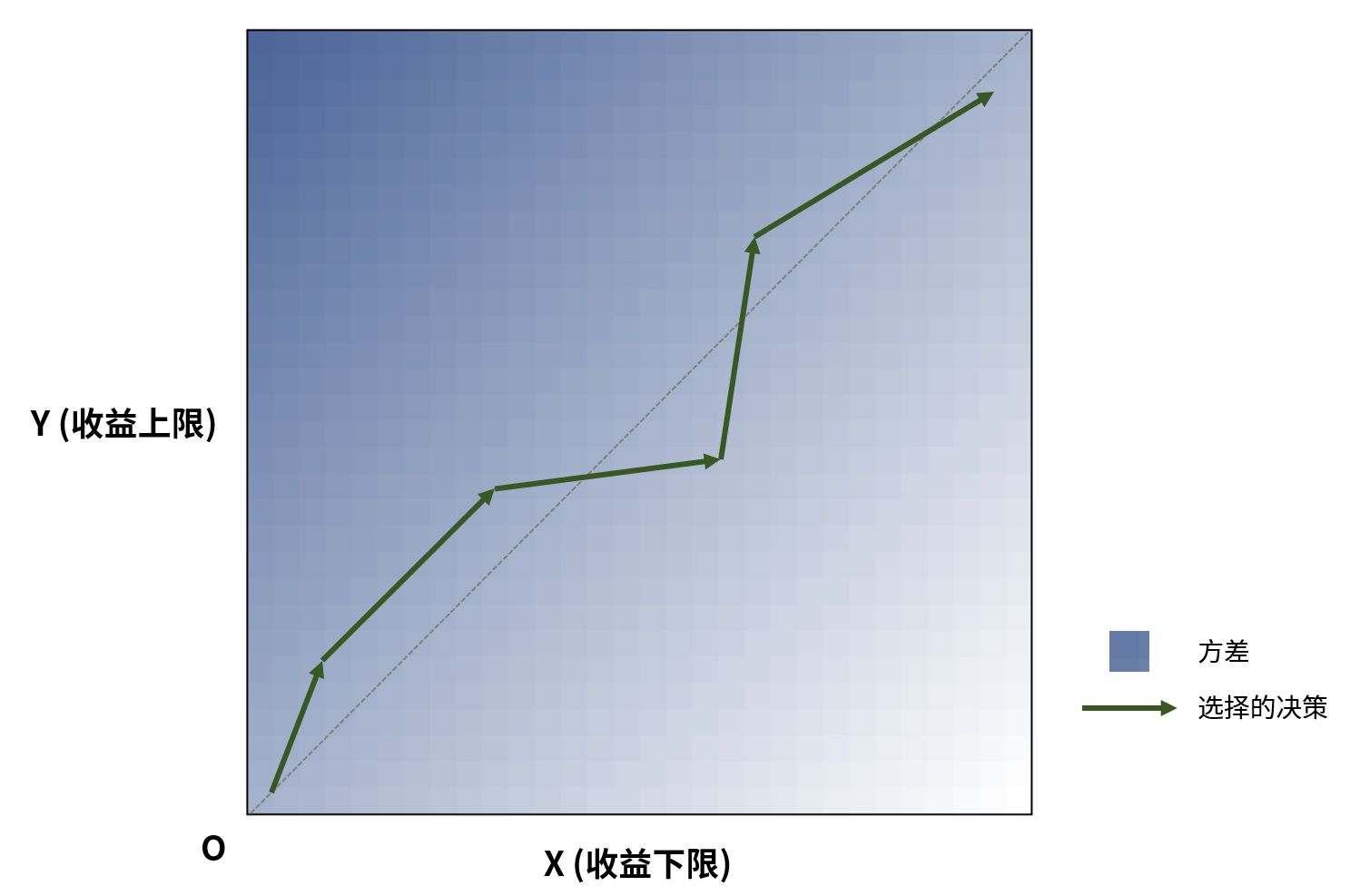
同上,只不過背景顏色代表了收益的方差而非期望。向上前進會導致方差增加,向右前進會導致方差減少
現在來關注這些決策對應的方差變化。箭頭更偏向上的決策可以被認為是“冒險決策”,這會導致方差增加;而箭頭更偏向右的決策可以被認為是“穩妥決策”,這會導致方差減少。
總結一下,在這個分析框架中,如果想創建出一個“有趣的決策”,我們可以遵循以下規律:
- 創建一些A類決策,使得這些選擇能夠增加收益上限,也會增加收益的方差,給遊戲帶來更多不確定性。對應著圖中偏向上的決策箭頭,在方差分佈圖上沿著這個箭頭走,顏色會變深。
- 創建一些B類決策,使得這些選擇能夠增加收益下限,也會降低收益的方差,給遊戲帶來更多可控性。對應著圖中偏向右的決策箭頭,在方差分佈圖上沿著這個箭頭走,顏色會變淺。
- 遊戲勝利要求玩家選擇A類決策和B類決策的數量大致保持均衡。這對應了橙色背景的期望分佈圖中,最高的收益區域集中在右上角(顏色最深)。
- 玩家需要根據場上的局勢,評估何時選擇哪類決策。這意味著兩種決策對應的決策箭頭(長度和方向)必須有一定的變化性(根據場上局勢不同而有所區別),而不能令決策的收益始終一成不變。
這四條規律會在第二章再次提到。
之所以要引入這麼多數學概念,解釋這麼多內容。我想意義在於,我們可以真的拉來一個遊戲,來定量地分析,它提供的決策是否符合這個框架。
正好,這次就把我做的這個遊戲《豐饒女神之骰》拉來分析吧。
雖然它只是一次Gamejam中的倉促之作,但我在思考遊戲框架時確實使用了一些上面的分析方法。我無法下定論說,這個框架在遊戲中最後的實現效果是理想的,但是,姑且作為一個例子,供大家參考吧。
二 《豐饒女神之骰》中的兩種決策
首先說結論,這也是件稍微有一些反直覺的事情:
《豐饒女神之骰》中的A類決策(冒險決策)對應了大部分卡牌的升級,而B類決策(穩妥決策)對應了區域的升級。這兩類決策,並沒有作為同一個系統中並列的兩個選項出現,而對應了兩種完全不同的機制。
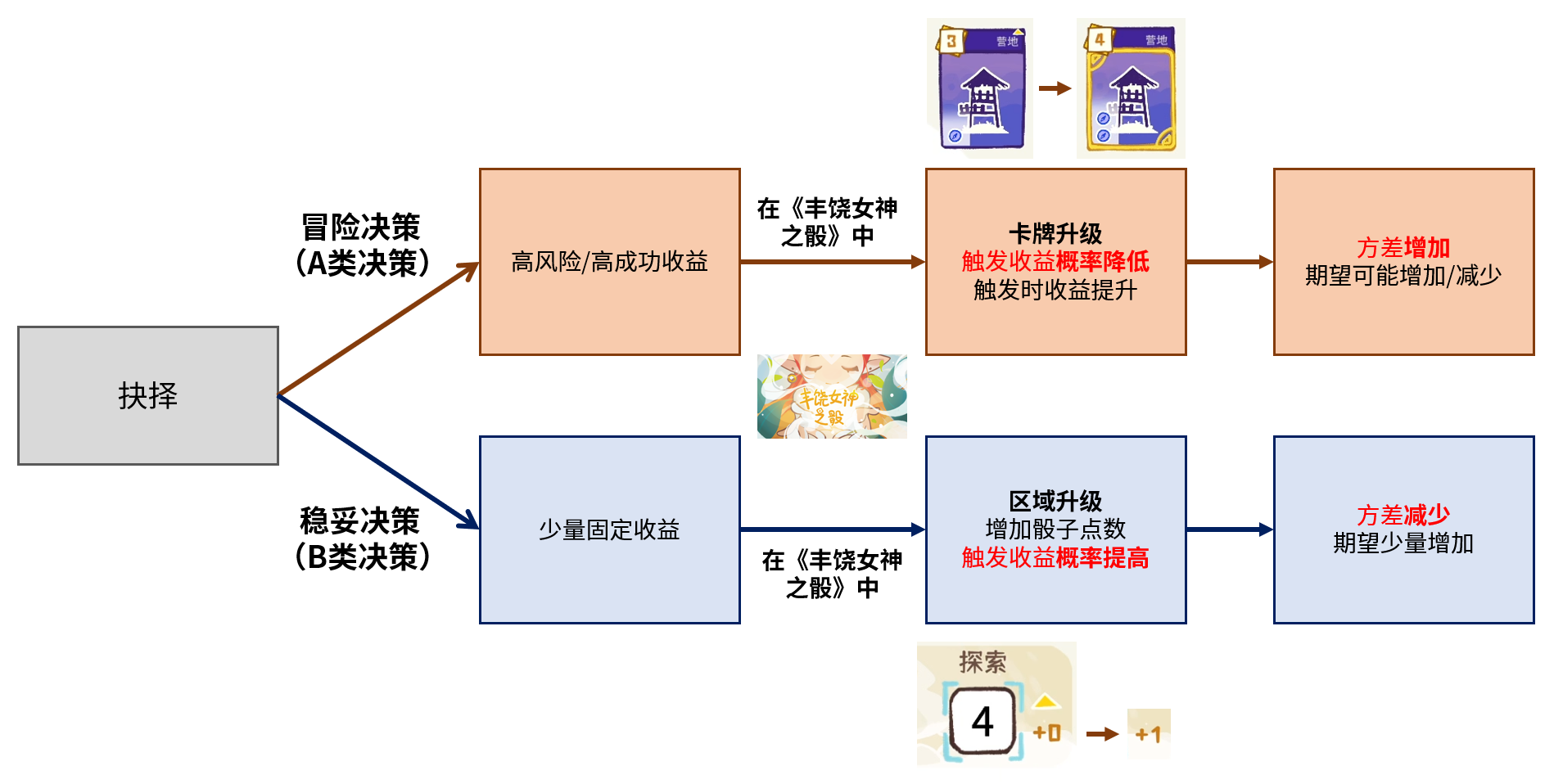
《豐饒女神之骰》中的決策設計思路
一般來說,在卡牌遊戲中,實現兩種決策的常見方式是選擇不同的卡牌,其中一張卡牌偏向於A類決策,而另一張偏向於B類決策。而在這個遊戲中,卡牌的選擇本身幾乎與兩類決策無關,隻影響你的發展路線選擇。而一般認為是穩妥正收益(B類決策)的“卡牌升級”,在遊戲中其實是具有風險的A類決策。真正的B類決策藏在了一個不太常見的機制——“區域升級”中。
我們先來看一個最簡單的原始模型。如果有體驗過這款遊戲(非常感謝!),應該能迅速知道我在說什麼,但即使沒有體驗過也沒關係,因為這個模型很簡單:
假設你每回合會扔出一個骰子,骰子為純隨機的1~6六面骰子。在初始設定下,如果你擲到3點(目標點數)或者更高,就能拿到一個蘋果。現在你有兩個強化的選擇:
- A強化:將目標點數增加1,但是成功後獲得的蘋果也增加1個;(舉例:在強化一次之後,當你擲出4點或更高時,可以獲得2個蘋果,但擲出3點就不能得到任何東西了)
- B強化:將你的所有骰子點數增加1。(舉例:在強化一次之後,你擲出的2點被視為3點)
假設在每個回合結束後,你都能選擇其中一個選項進行強化。每項強化可以進行多次。你要如何保證5回合過去之後,期望獲得的蘋果總數最多呢?
假設我們進行了x次B強化,以及y次A強化。可以計算出,這回合獲得蘋果的概率是:
p = Clamp((4 + x - y) / 6, 0, 1)
(Clamp函數將概率限制在0~1之間)
這回合如果獲得了蘋果,獲得的個數是:
w = 1 + y
所以,獲得蘋果數量的期望是:
E = wp
獲得蘋果數量的方差是:
σ² = w²p(1-p)
我們直接把這些計算方法代入上面的圖像中,作為期望值和方差值:
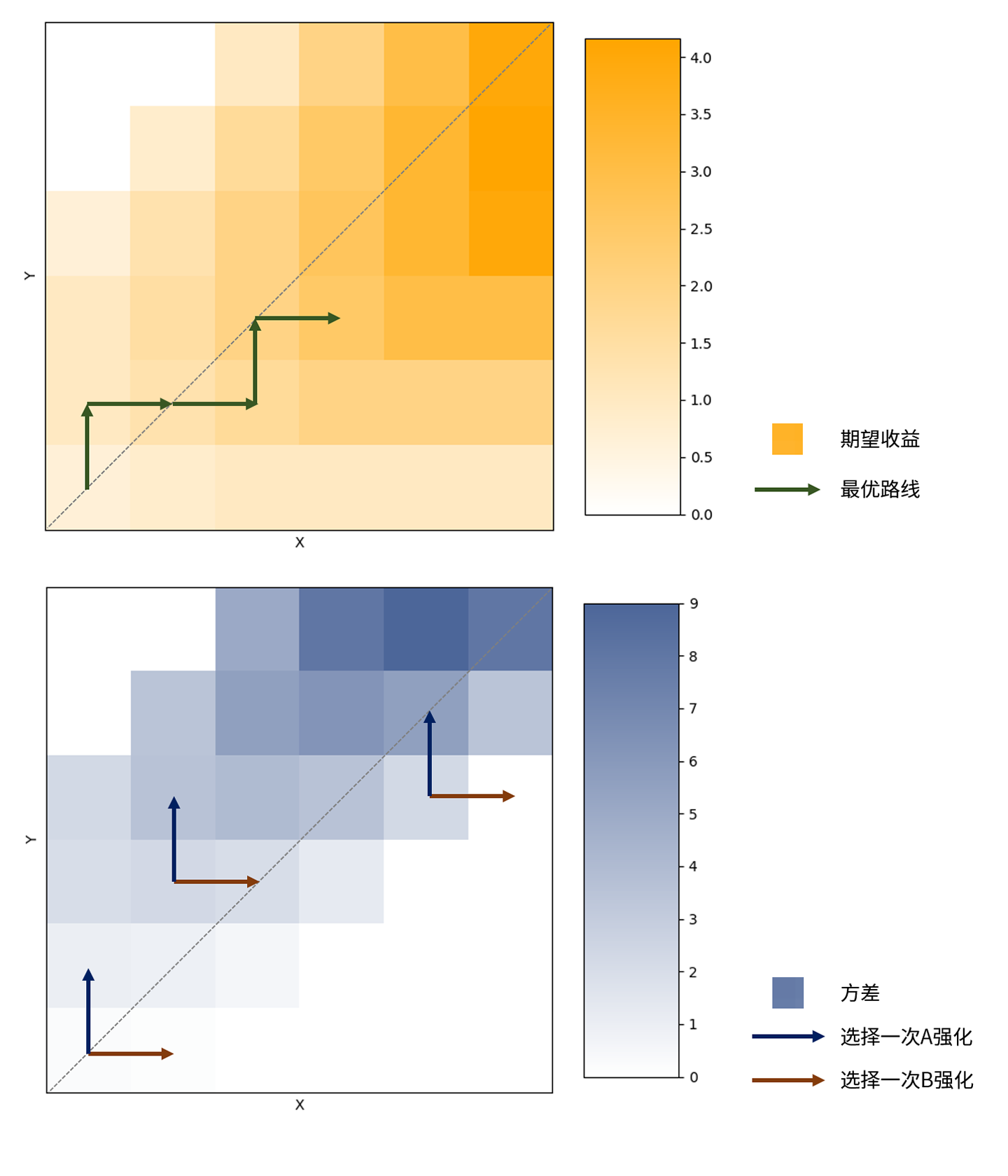
上述模型下,經過數次強化後,獲得蘋果數量期望與方差的分佈圖
其中X座標代表了已選擇B強化(增加骰子點數)的次數,而Y座標代表了已選擇A強化(增加目標點數和產出)的次數。
首先看第一張圖,也就是期望分佈圖,可以看出,這是基本符合我們在上一章討論的規律的。收益較高的區域集中在右上角,也就意味著遊戲勝利(較高的收益)要求玩家選擇A類決策和B類決策的數量基本保持均衡,換言之,玩家經過的決策路徑應當始終在虛線附近(虛線上的點代表了選擇同樣數量的A強化與B強化)。
其次看第二張圖,方差分佈圖。如果我們假設玩家始終位於虛線附近(較高收益的區域)做決策,那麼他們的每一個選擇A強化或B強化的決策,恰好對應了上面說的A類決策與B類決策,也即:前者增加方差(顏色變深),而後者減小方差(顏色變淺)。圖中的幾組箭頭就是幾個典型的例子。
和上一章的理想方差分佈圖有所不同的是,此圖左上角的方差反而減少了。這是因為在此時事件的觸發概率非常接近或者等於0,但在正常情況下,決策幾乎不會走到這個區域。
那麼最後一條需要驗證的規律,就是“玩家需要根據場上的局勢,評估何時選擇哪類決策”。在這個遊戲中,這條規律體現為:你可以先擲出骰子,再選擇如何強化。這會導致在當前回合的一次即時收益,影響兩種決策的收益天平。
例如,在上面的例子中,假設玩家已經選擇了兩次A強化,且在下個回合開始前,事先得知自己將擲出6點,並且要進行一次A強化還是B強化的抉擇。此時,即使再次選擇A強化,增加了目標點數,當前回合依然能夠100%觸發收益,並且額外獲得了1個蘋果。雖然這個行為會導致下個回合的期望偏離最優,但本回合獲得的資源,也足以與未來的期望收益略微降低構成一個小型的決策點。
在正式的遊戲中,雖然具體情況和上面的簡化模型有所不同,但這種A類決策與B類決策之間的抉擇,從第二回合便開始了(在第一回閤中無法升級,且骰子的結果是鎖定的):

第2回合開始時,需要面對的幾種抉擇
(注:圖上幾張卡牌的升級效果均為“難度等級+1,且對應產出+1”,即A強化。而左邊的四個“+0”上的箭頭代表著你還可以強化放置於該區域的骰子點數,使其視為+1,即B強化。)
假設這是一局遊戲的第二回合,你擁有的資源(木材)只允許你升級其中一個卡牌或區域。
在這個回合,你投出了很高的點數。就算你選擇升級卡牌,也能拿滿所有獎勵。但這意味著如果下個回合出現較低點數的骰子,它很可能將毫無作用。當然,你也可以選擇保留升級資源,在下個回合擲出低點數骰子之後,再臨時升級想要觸發的區域。
是冒著未來運氣不好會空過的風險,升級卡牌並即刻多拿一個資源呢(A類決策)?還是選擇將資源留著,在未來運氣不好時升級區域增加點數,保證較高的卡牌觸發率呢(B類決策)?
這就是一個典型的、如上一章所說的,“冒險決策”與“穩妥決策”之間的抉擇。
在實際遊戲中,由於玩家能夠擁有大量卡牌和四個區域,考慮到各種因素,每張卡牌被設定為只能升級一次。而在上面的簡化模型中,作為A類決策來展示的“卡牌的多次升級”,事實上被拆分為了“多張卡牌的分別升級”,“卡牌的增益效果”以及“逐漸能選擇拿到難度等級更高但產出也更高的卡牌”。但其核心依然在於“大部分卡牌產出變多的同時,會增加難度等級,從而作為A類決策出現”。另一方面,區域的多次升級被完整地繼承到了正式的遊戲流程中,起到的效果也十分相仿。
(此外,在實際遊戲中,區域升級帶來的另一個B類決策是骰面的升級,這個會在下一章簡單提一下)
最後,這個系統在最終的實現層面,其實也是有不少問題的。最顯著的問題出現在:這個較為反直覺的系統,使得在玩家真正熟悉整個系統之前,都會遭受持續較長時間的一個明顯負面體驗:“這個遊戲運氣因素過大”。
在這幾天的思考之後,我認為可能的原因是:在玩家多次進行了卡牌升級後,根據大部分遊戲的普遍直覺,會認為自己做出了大量B類決策,這本應讓自己的發展非常穩健。但事實上則是在不知不覺中做出了大量A類決策,導致了只有靠運氣roll到高的骰子點數才能不空過。
(不一定對,歡迎大家對此提出更多的想法與建議)
雖然意識到這件事本身的過程會迎來一些“尤里卡時刻”,但是,這件事的反直覺性導致整體的學習曲線大概並不算很好。在這一點的設計與引導上,這個遊戲有很大的改進空間。
三 骰子、隨機性和Build
區域升級作為遊戲中的B類決策,可以增加對應區域的骰子點數以降低方差。但遊戲中的B類決策,只有這個就足夠了嗎?
也許在調整數值之後,是夠的,但這似乎不夠豐富。
構成遊戲豐富性和變化性的另一塊重要拼圖,則是骰面的升級。
在遊戲中,你一共擁有3個骰子,當你每次對區域進行升級時,還可以對一個骰面進行升級。每個骰面只能升級一次,並且你只能按照原始點數1~6的順序,依次升級每個骰子的各個骰面。換句話說,除了Build場上的牌以外,你還可以對骰子作出一些特殊的Build。
當你第一次升級區域時,你會從三個骰子中選擇1個,將其點數為1的那面進行強化,每個骰子會隨機提供一個選項,如下圖所示:
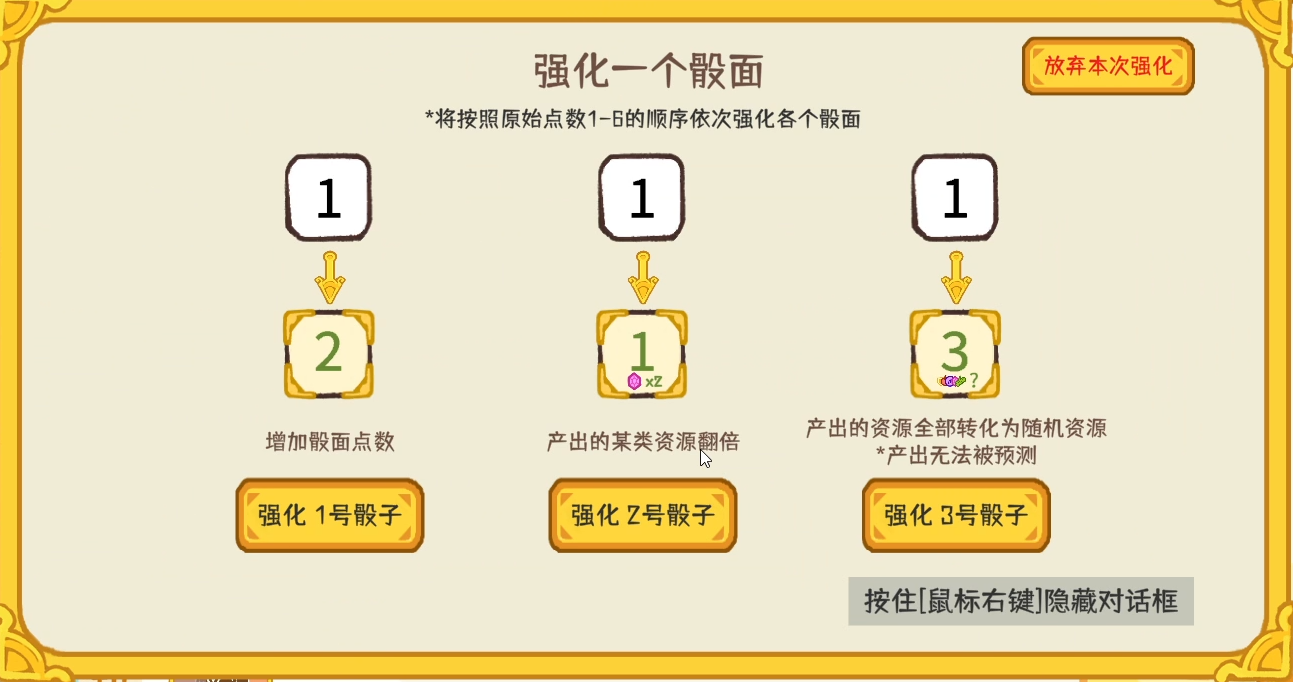
骰面強化的界面,這是遊戲中的首次強化,因此只能在3個1點骰面中選擇1個進行強化
當你強化了某個骰子的1點所在面之後,下次強化時,這裡就會出現該骰子2點所在面的強化選項了。總而言之,前期你只能強化較低的點數,而後期隨著強化次數的增多,就可以慢慢強化骰子上較高的點數。其中,大部分強化都能夠增加骰麵點數,少部分強化會以減少其骰麵點數,使某類資源的產出翻倍。
之所以要規定“必須從1到6依次強化各個骰面”,而不是隨機出現三個未強化的骰面,或是讓玩家直接挑選想要強化的那個骰面,其實有多個考慮因素,主要有下面幾個:
- 前期最大的失敗和負面運氣來源——點數為1的骰面,可以通過作為B類決策的區域強化來將其點數變為2(大概率),從而永遠避免擲出1點。而2點骰子在區域點數+1的幫助下,前期能觸發很多尚未升級的卡牌,是有作用的。這樣的話,升級區域作為最主要的B類決策,其效果更好、更明顯,也能更有效地降低運氣帶來的不確定性(也就是方差)。其中最主要一個點是,如果你在前三個回合不幸擲出了很多個1點,可以直接通過升級區域進行骰子強化,來大概率將一個已擲出的1點骰子立刻變為可用的2點。
- 與上述的B強化類決策的“點數增加”相比,低點數骰面的某些技能,也能提供一些額外的A類決策選項,最明顯的如“減少點數但某種產出變為雙倍”。對於高點數的骰子而言,這種強化的價值一般遠超“骰麵點數+1”,因為即使6點的骰子減到了5點,也能觸發大部分卡牌,幾乎不存在風險,也就不能構成有效的A類決策。但對於一個1點或2點的骰子而言,這幾乎意味著你要放棄這個骰面在前期發揮的作用(增加風險),在後期區域等級提升之後,才能穩定地觸發並獲得大量收益。這就出現了一種類似於“犧牲前期穩定性,而獲得後期收益”的新選項,增加了遊戲的決策深度。
- 避免了自由選擇18個骰面強化時造成的決策過載。也避免了隨機強化骰面進一步增加這款遊戲的隨機性,而是多了一個有可靠預期的強化/Build內容。
骰子還能提供一些很有意思的build,比如問號骰子的妙用,可以幫助處理溢出防護值的同時,在前期獲得一些珍貴的晶石資源。由於篇幅問題,在這裡就不對上述內容展開分析了。
四 關於難度設計的一些雜談
最後想聊一下《豐饒女神之骰》的難度梯度設計。作為一款以數值為核心的策略遊戲,加入難度選項是必須的。
在這款遊戲中,遊戲的難度增加當然意味著數值提升。但提升哪些數值,要如何提升,我認為也是有很大講究的。一個好的難度設計,會引導玩家在難度逐漸提升的時候,依次重新理解各個系統機制的重要性,與此同時不要讓任何一個難度出現信息過載或學習成本過高的情況。
在這款遊戲中,設計各個難度的大致思路如下:
標準難度。作為附帶新手教程的、玩家首次接觸的難度,需要保證各個機制都是完整的,並且需要給予充足的容錯率和探索遊戲系統的時間,儘量避免玩家因為經驗不足而直接導致失敗。為此,應該放寬一切內容的“時限”並減少直接導致失敗的可能性:作為主要壓力點和失敗點的暴風雪,其威力的增加速度較為緩慢。即使因為種種原因多花費了很多回合,緩慢增長的暴風雪威力也不會輕鬆將玩家擊敗。而需要在時限內解決、需要玩家迅速響應的事件卡,也設定了較為寬鬆的時間。其次,作為失敗另一大原因的食物壓力,也在此難度設置為了一個較為平緩的值。
困難難度。與標準難度相比,這個難度強調的主要是“時限”。在玩家通過了標準難度,初步瞭解了整個遊戲系統與流程的情況下,困難難度會非常強調回合數的重要性:時限較短的事件卡要求玩家能夠靈活應對各類事件,甚至為了解決事件來改變一些決策。而更重要的是,在遊戲的中後期,暴風雪的威力有了巨大的提升,尤其是第三次連續暴風雪(大約在遊戲的55回合),被設定為了一個極難扛過的強度,將遊戲拖至此時將大概率迎來失敗。這意味著玩家必須熟悉通關的流程和要求,並且儘量在55回合之前達成三種通關條件之一。甚至為此在中期就要規劃獲得通關所需的材料,而不能慢慢等待各項設施全部建造完成、資源大量溢出後,選擇一個結局通關。
非常困難難度。作為遊戲的最高難度,與困難難度相比,這個難度強調了遊戲中最後兩個重要維度的作用:食物與探索點數。在其餘難度下,玩家可能會發現,只需要較少的食物與探索卡就足以支撐起通關的要求,在大部分時間內專注於採集木材和建造防護即可。但在最高難度下,食物與探索點數的壓力被提高,這意味著一部分原本用於採集和防護的骰子資源與卡牌資源,需要重新考慮被分配的方式,尤其是在資源十分珍貴的前期。遊戲的四類區域與卡牌,也從“兩強兩弱”的價值分佈變成了“四種資源都很急很缺”。這顯然讓思考的複雜度提高了不少,與“最高難度”相般配。最高難度中四種資源的相對價值,也是在調整這款遊戲的數值時,真正的平衡基準線。

遊戲中的三種難度設計
按照上面的思路,我最終敲定了《豐饒女神之骰》中各個難度等級的機制與數值變化。在這裡也很希望在這裡收到更多的玩家反饋(畢竟自己並不能“真正”模擬初次接觸遊戲的玩家),如果想要分享挑戰高難度時或好或壞的遊戲體驗,或是想對難度等級提出一些改進意見,歡迎在評論區留言討論!
結語
非常非常感謝大家耐心看到這裡。這次BOOOM活動的體驗很不錯,收穫了很多寶貴的開發經驗,也很高興能有這樣一次機會,與各位優秀的玩家和開發者交流。希望未來也能與大家多多交流、共同進步!