總結
- 從底注11開始,小丑牌的難度顯著增加。
- 無盡模式確實是無限的,你不能真正“通關遊戲”。
契機
我經常發現自己組一個還不錯的卡組,但在達到某個底注級別後,遊戲難度會急劇增加。戰勝盲注的分數變得如此之大,以至於遊戲感覺無法戰勝。
於是,我很好奇遊戲到底是如何計算盲注分數的。從遊戲包中提取了 Lua 文件後,使用關鍵字“300”(初始盲注金額),我找到了 misc_functions.lua 中的get_blind_amount(ante)。
發現
以下是完整方法:
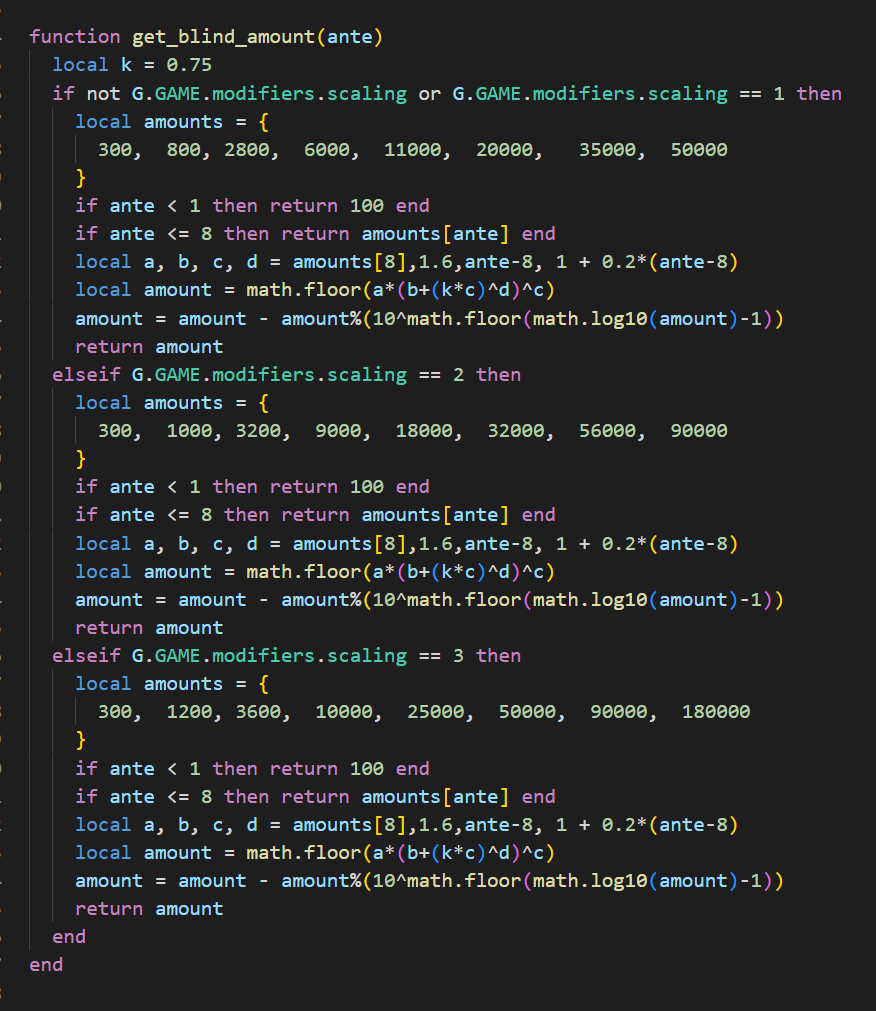
這個方法很好分析:
有三個 if 語句,根據不同的ante_scaling參數來設置每一回合的初始金額,其中 1 是最低,3 是最高。

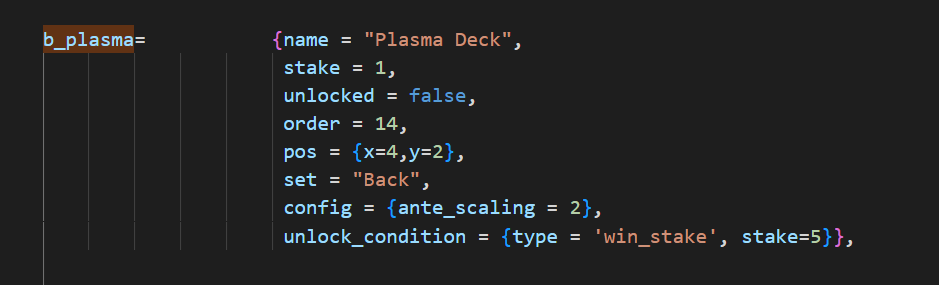
例如,在game.lua這個文件中,我們會發現等離子卡組為被設置成了2。
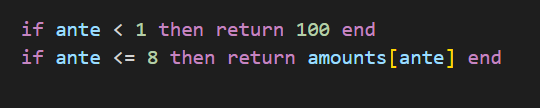
每個if判斷語句的剩餘代碼相同,根據盲注等級(ante)設置分數(amount)。當盲注小於1時,分數為100。當盲注小於等於8時,分數從分數列表(amounts)中取。

然後,代碼使用盲注等級和分數列表設置參數 a, b, c, d 來計算當盲注大於8時的盲注金額。


隨著盲注等級n趨近無窮,由於 c 和 d 是關於n的的線性函數,A 實際上超越了我們熟知的指數增長,進入迭代冪次的領域。這一個很有意思的數學概念,在這裡就不過多介紹了。
分析
底注等級 = 8
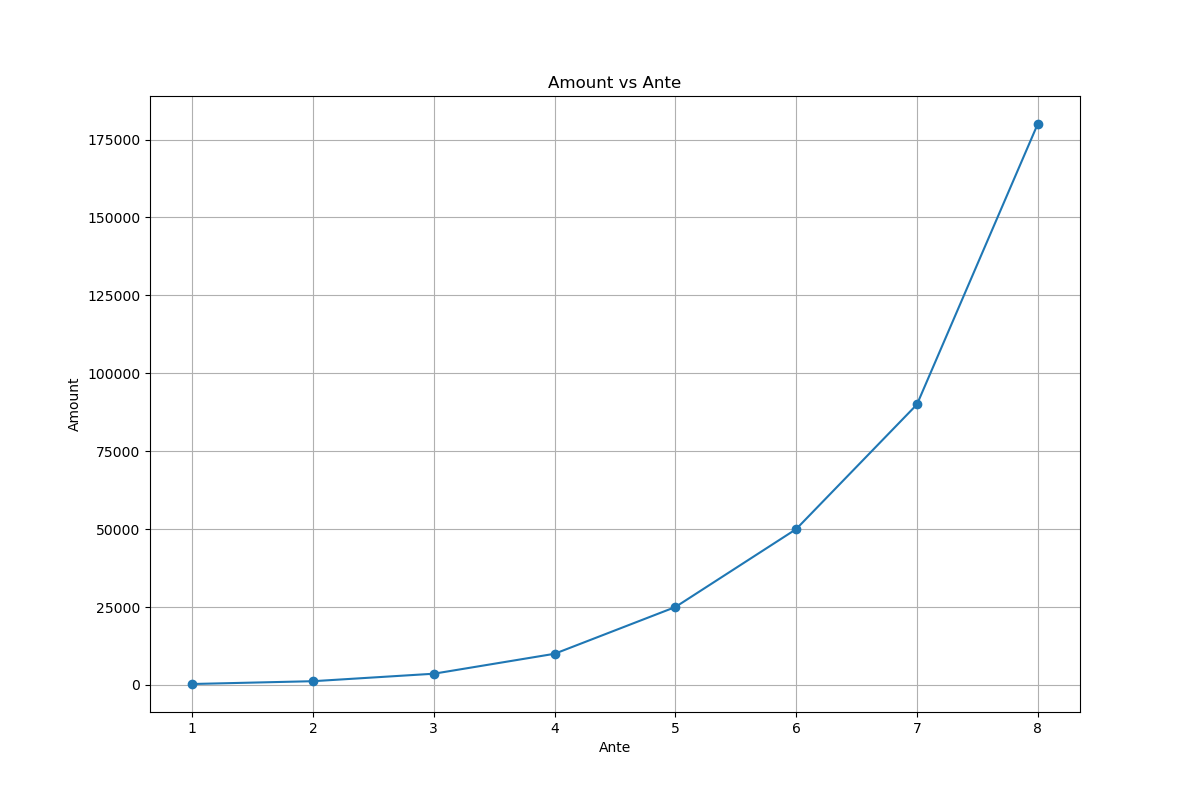
在觀察曲線時,發現無盡模式在底注等級為1到8時,曲線較為平滑,盲注分數還算“可控”。
底注等級 = 9,c=1,d=1.2,成長性還不錯,但和之前的數差別不大。
底注等級 = 10,c=2,d=1.4,成長性更明顯,但可能還沒有顯著超過最後一步計算(A - A mod 10那一項)的舍入閾值 。
底注等級 = 11,c=3,d=1.6,成長性非常顯著,從圖中可以看到明顯的飛躍,盲注金額飆升。
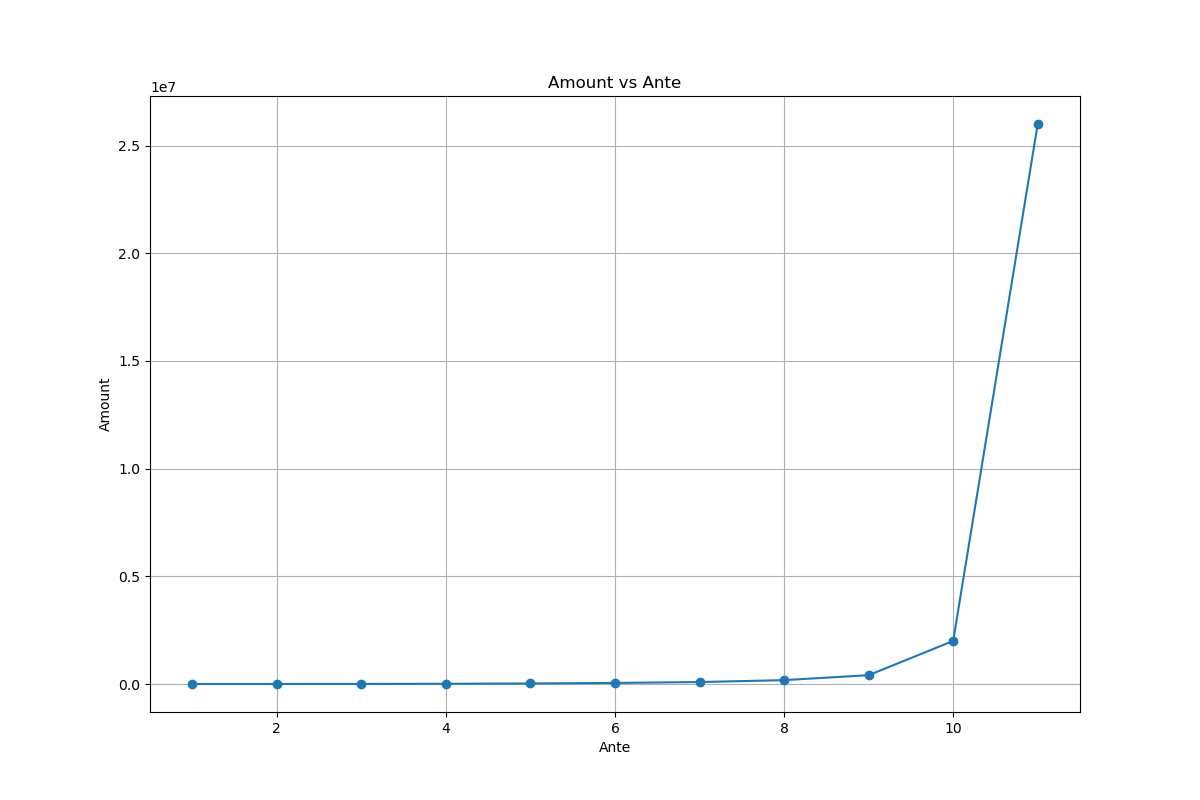
注意,這裡我想表達的“難度”其實是感知上的,用了“還不錯”、“明顯”、“顯著”等修飾詞。本質上,在底注到達9後,程序已經採用了迭代冪次運算,只不過在9和10時,我們”感覺“表現沒有那麼誇張。
拓展
理論上,玩家能達到的最高盲注級別是什麼?考慮到 Lua 的最大正浮點數大約為1.8e308,在 盲注 38 時,分數約為1e289。這表明在盲注39 時,這個數字將超過程序的計算能力。網上的視頻表明,目標分數為nan,而你的得分為naneinf。

www.reddit.com/r/balatro/comments/1bo1c25/i_finally_beat_ante_39_with_glass_cards_perkeo/
不過到這裡遊戲就自動結束了。
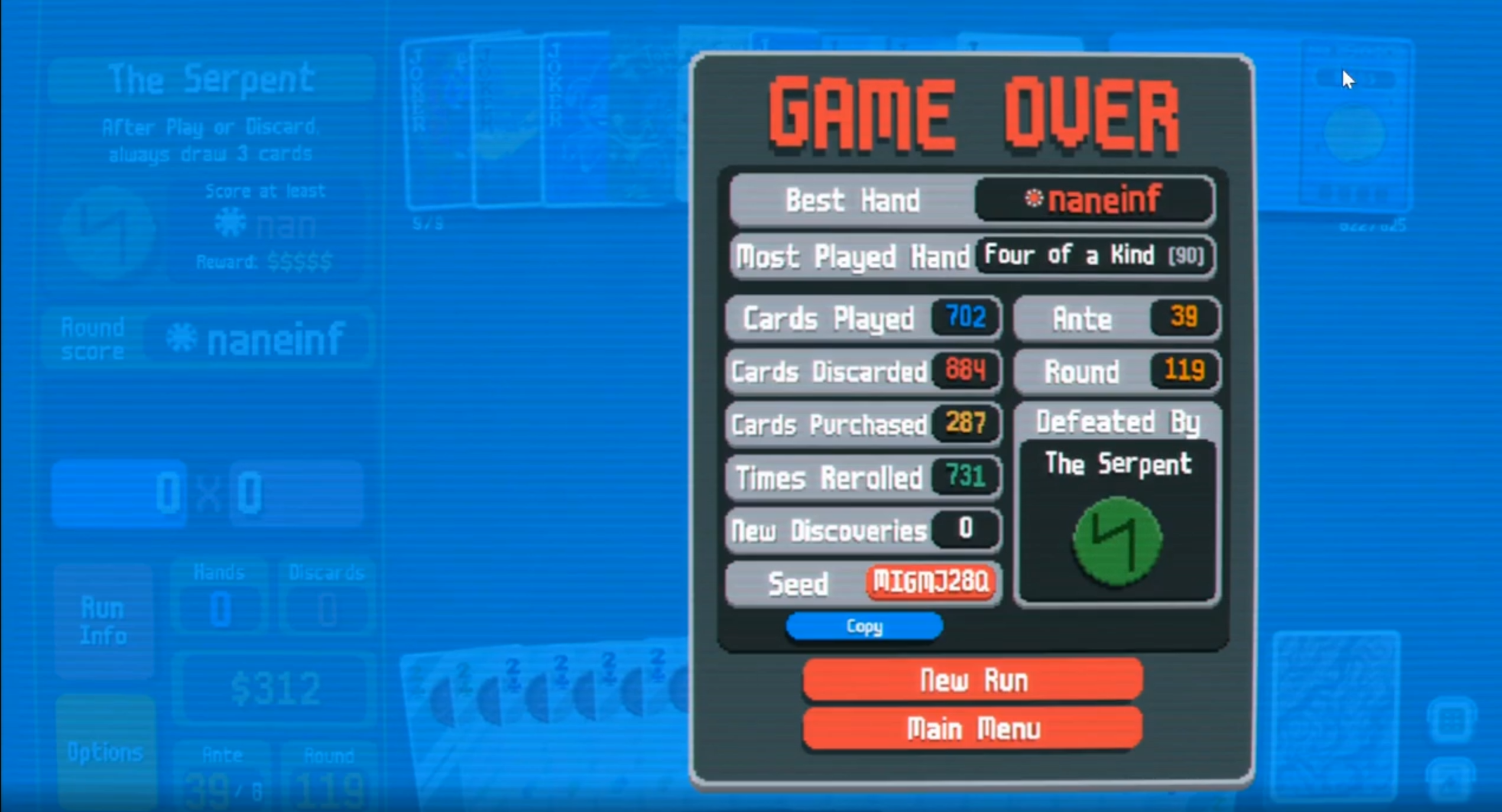
www.reddit.com/r/balatro/comments/1bo1c25/i_finally_beat_ante_39_with_glass_cards_perkeo/
收穫
- 遊戲數值設計也是一門學問。參數和函數的選取考驗了開發者對數學和遊戲機制的跨學科理解。
- 看遊戲底層代碼的分析過程還是很有意思的!雖說這個問題沒有那麼複雜,但通過現象找到本質真的能讓人感覺到智力上的愉悅。
- 從代碼格式上來看,Balatro 其實寫得不算很整潔,這說明其實你不需要很深的編程能力就可以開發出一款相當好玩的遊戲。希望這能給遊戲創作者們以信心哈哈。
歡迎評論區交流!