总结
- 从底注11开始,小丑牌的难度显著增加。
- 无尽模式确实是无限的,你不能真正“通关游戏”。
契机
我经常发现自己组一个还不错的卡组,但在达到某个底注级别后,游戏难度会急剧增加。战胜盲注的分数变得如此之大,以至于游戏感觉无法战胜。
于是,我很好奇游戏到底是如何计算盲注分数的。从游戏包中提取了 Lua 文件后,使用关键字“300”(初始盲注金额),我找到了 misc_functions.lua 中的get_blind_amount(ante)。
发现
以下是完整方法:
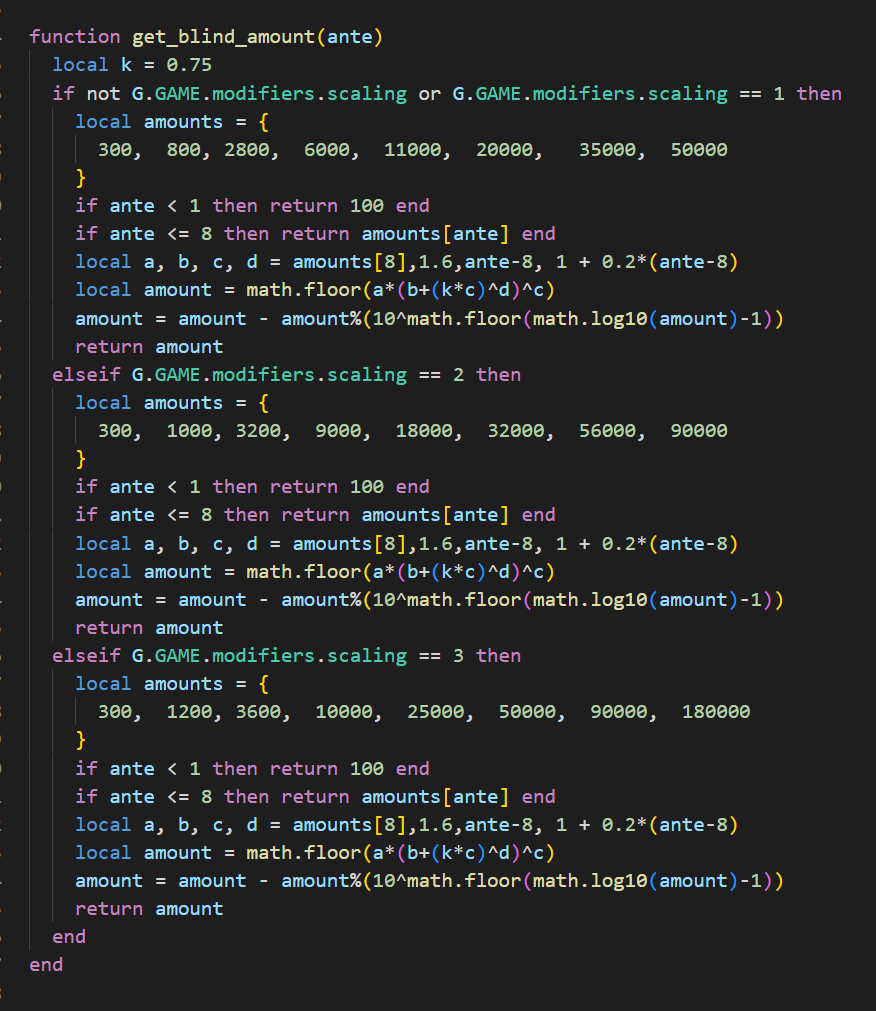
这个方法很好分析:
有三个 if 语句,根据不同的ante_scaling参数来设置每一回合的初始金额,其中 1 是最低,3 是最高。

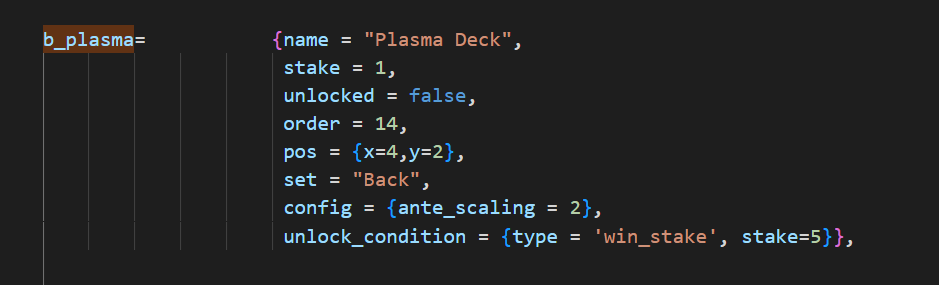
例如,在game.lua这个文件中,我们会发现等离子卡组为被设置成了2。
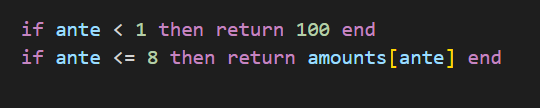
每个if判断语句的剩余代码相同,根据盲注等级(ante)设置分数(amount)。当盲注小于1时,分数为100。当盲注小于等于8时,分数从分数列表(amounts)中取。

然后,代码使用盲注等级和分数列表设置参数 a, b, c, d 来计算当盲注大于8时的盲注金额。


随着盲注等级n趋近无穷,由于 c 和 d 是关于n的的线性函数,A 实际上超越了我们熟知的指数增长,进入迭代幂次的领域。这一个很有意思的数学概念,在这里就不过多介绍了。
分析
底注等级 = 8
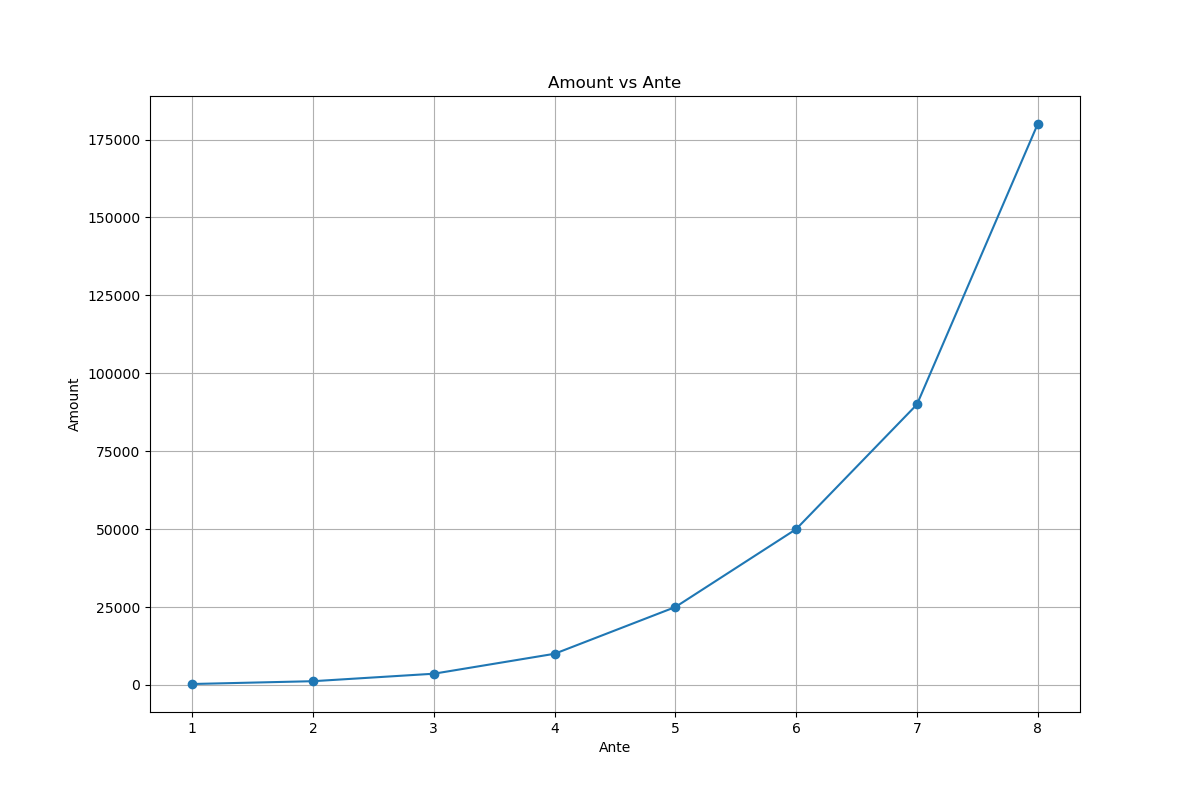
在观察曲线时,发现无尽模式在底注等级为1到8时,曲线较为平滑,盲注分数还算“可控”。
底注等级 = 9,c=1,d=1.2,成长性还不错,但和之前的数差别不大。
底注等级 = 10,c=2,d=1.4,成长性更明显,但可能还没有显著超过最后一步计算(A - A mod 10那一项)的舍入阈值 。
底注等级 = 11,c=3,d=1.6,成长性非常显著,从图中可以看到明显的飞跃,盲注金额飙升。
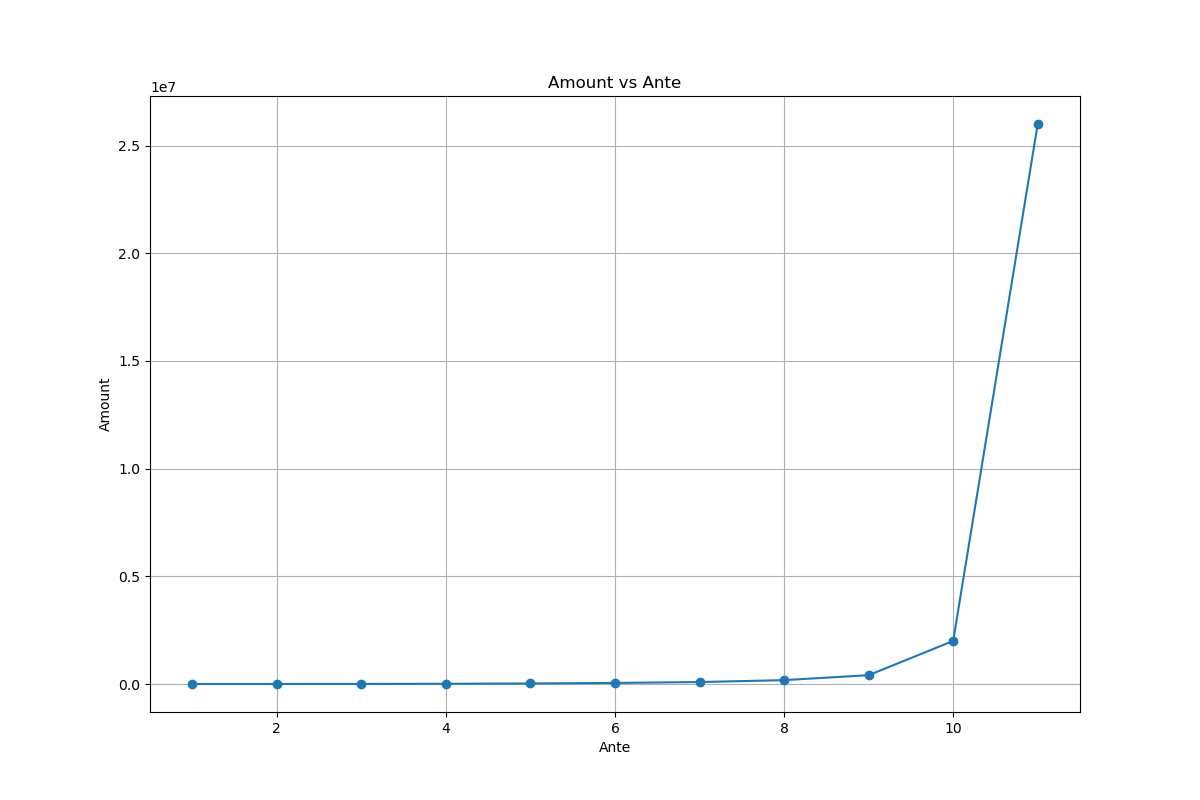
注意,这里我想表达的“难度”其实是感知上的,用了“还不错”、“明显”、“显著”等修饰词。本质上,在底注到达9后,程序已经采用了迭代幂次运算,只不过在9和10时,我们”感觉“表现没有那么夸张。
拓展
理论上,玩家能达到的最高盲注级别是什么?考虑到 Lua 的最大正浮点数大约为1.8e308,在 盲注 38 时,分数约为1e289。这表明在盲注39 时,这个数字将超过程序的计算能力。网上的视频表明,目标分数为nan,而你的得分为naneinf。

www.reddit.com/r/balatro/comments/1bo1c25/i_finally_beat_ante_39_with_glass_cards_perkeo/
不过到这里游戏就自动结束了。
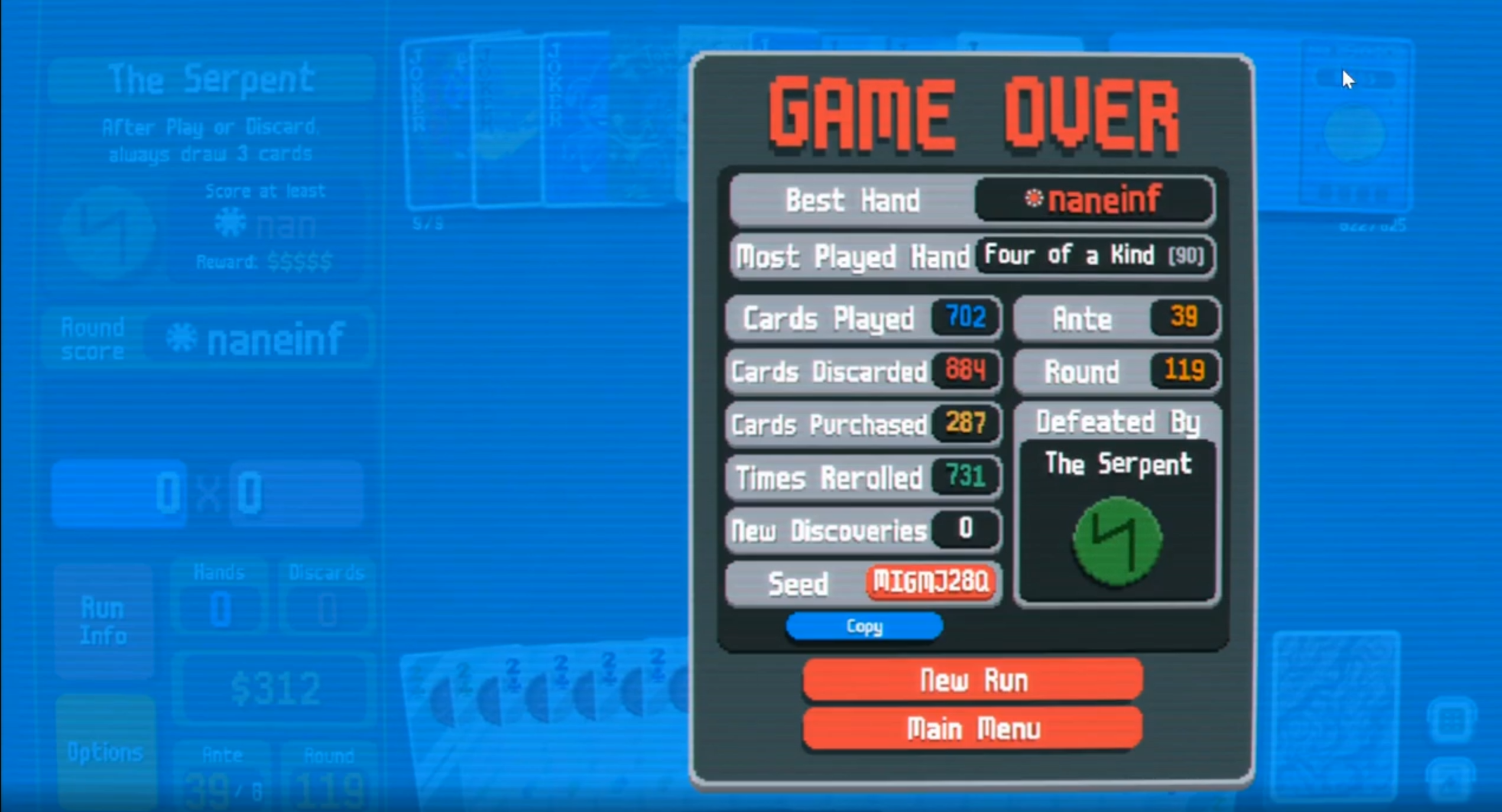
www.reddit.com/r/balatro/comments/1bo1c25/i_finally_beat_ante_39_with_glass_cards_perkeo/
收获
- 游戏数值设计也是一门学问。参数和函数的选取考验了开发者对数学和游戏机制的跨学科理解。
- 看游戏底层代码的分析过程还是很有意思的!虽说这个问题没有那么复杂,但通过现象找到本质真的能让人感觉到智力上的愉悦。
- 从代码格式上来看,Balatro 其实写得不算很整洁,这说明其实你不需要很深的编程能力就可以开发出一款相当好玩的游戏。希望这能给游戏创作者们以信心哈哈。
欢迎评论区交流!