世界上最快的運動員,追不上一隻普通的烏龜?古希臘“芝諾悖論”因其淺顯易懂的描述和顛覆直覺的推論為人所熟知,千百年間受到了廣泛的討論和爭議。直到近現代量子力學的研究不斷進步,物理界四神獸之一的芝諾烏龜才被徹底打敗。本篇文章就帶大家討論一下,物理學究竟如何駁倒了惱人的芝諾悖論。
前車之鑑
人類探索無限小的歷史已經不可細考。古印度教的勝論派主張世界由不可分割的極微組合而成;中國《莊子·雜篇》中“一尺之棰,日取其半,萬事不竭”的論斷則認為不存在最小的不可分割的尺度;古希臘愛麗亞學派的代表人物芝諾多羅斯提出的芝諾悖論思考了時間與空間的分割和連續問題。芝諾悖論中最為有名的阿喀琉斯悖論的主要內容是:喀琉斯是古希臘最有名的運動員,他將和一隻起跑時領先他一段路的烏龜賽跑,當阿喀琉斯跑完起跑時二者相差的路徑時烏龜也前進了一段距離;當阿喀琉斯再次追完二者相差路程,烏龜就又前進了下一段更小的距離……如此循環,阿喀琉斯只會不斷接近但卻始終追不上烏龜。
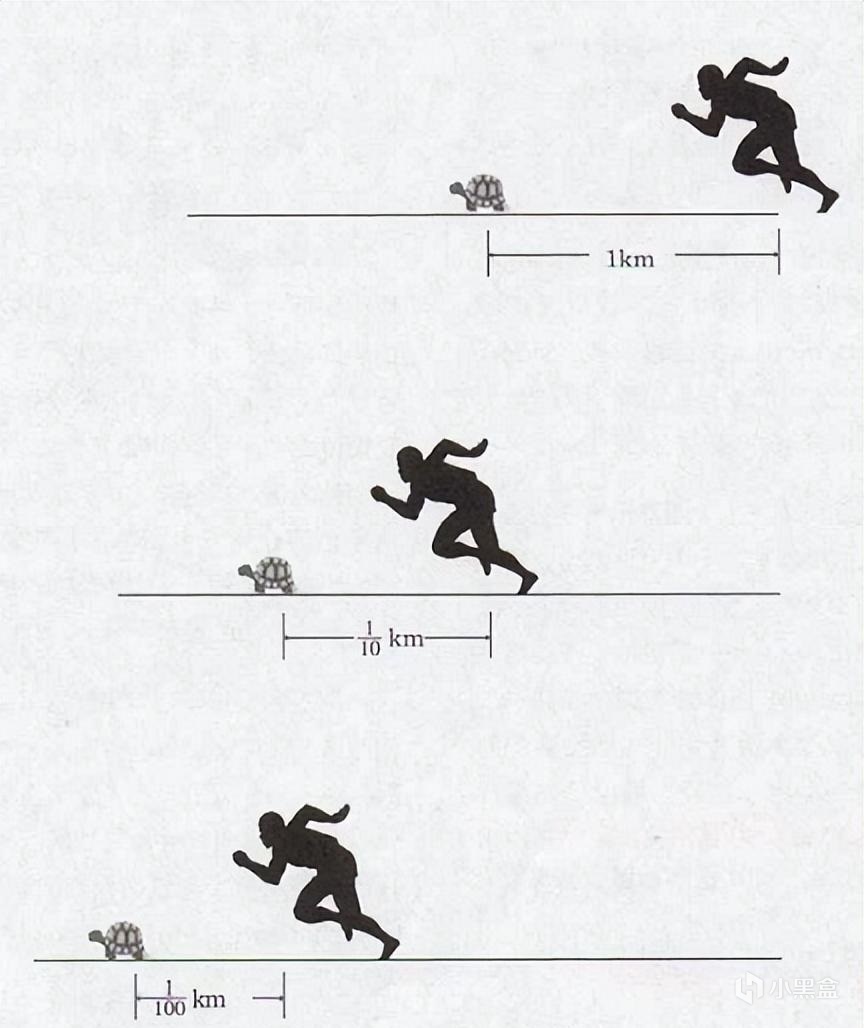
阿喀琉斯永遠追不上烏龜
這個看似簡單的問題,包含著古希臘哲學家芝諾多羅斯對空間的思考。芝諾是古希臘愛麗亞學派的主要代表人物,主張時間和空間的可微性,即時間和空間都是可以無限進行分割的,並以此否定運動的存在。他所提出的四大悖論以通俗易懂的口吻提出了對於時空的思考。所以烏龜悖論也被稱為芝諾第二悖論。如果空間是可以不斷分割的,那麼阿喀琉斯和烏龜之間的距離就可以無限小,所以阿喀琉斯總是追不上烏龜。假如我們將這個問題反過來看,回到阿喀琉斯剛剛起跑邁出第一步的時候:阿喀琉斯要先把腳邁出1釐米,就必須先跨出0.5釐米;要跨出0.5釐米,就必須先跨出0.25釐米……如此持續地分下去,阿喀琉斯必須要經過無限個流程才能開始運動,因此阿喀琉斯永遠也不可能運動。芝諾就是用這樣簡單易懂的問題,表達了自己“時空可微、運動不存”的觀點。
阿喀琉斯追不上烏龜的答案顯然是錯誤的,如果真的如此,在另一個故事裡即便兔子睡得時間再長,烏龜也不可能取勝。那問題的真相是什麼呢?有一個有趣的說法是,因為阿喀琉斯總是追隨著烏龜的腳步,所以永遠也不可能超越烏龜。這個回答顯然足以對悖論做出字面的解釋。但我們必須知道包括芝諾的烏龜在內的物理學四大神獸,都只是更深刻的物理問題的抽象表達,只是物理學家為了更加生動地描述物理問題而講的童話故事。要真正打敗芝諾的烏龜,必須從問題的初衷入手:空間本身可以被無限細分嗎?
測不準和絕對的小
邁克爾·菲爾在著作《啤酒與肥皂》中稱量子力學為“研究絕對的小的物理學”。我們知道在經典物理學中,只要採取正確的測量手段就不會對測量對象造成影響。比如測量一輛車的位置和速度(或者說動量),只要用合適的器具正確測量,車的位置和速度總是確定的,不會因為測量的行為而改變。但是在量子力學的領域中,測量的對象是“絕對小的東西”。什麼是絕對小的東西?比如要測量一個電子的位置和動量,我們總是需要用其他的微觀粒子來碰撞這個電子,然後觀察粒子在碰撞前後的變化來判斷電子的狀態。但是對於電子這樣小的粒子來說,要準確測量位置就必須選用波長足夠短的光子才能測得更為精確;而光子波長越短能量越大,碰撞中對電子速度的影響也會越大,於是就無法準確測量電子的動量。如此以至於測量的動作改變了每一個被測量的電子的狀態從而產生了不可忽略的偏差,這時就可以說我們測量的對象是絕對小的東西,所做的研究也就歸屬量子力學。而所謂“不可忽略的偏差”的存在,被人們稱為“測不準原理”。
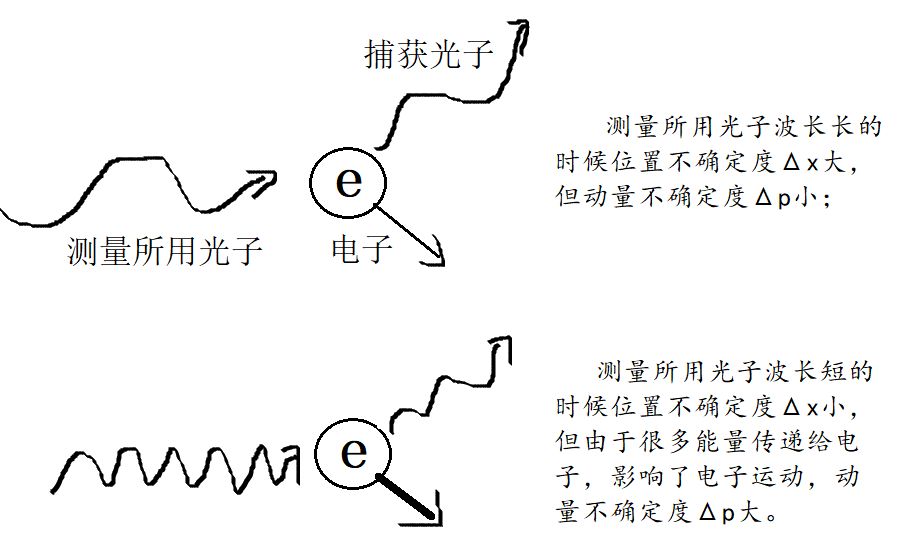
測量的動作會影響測量的結果
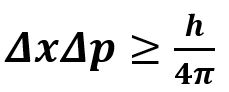
Δx為位置不確定度,Δp為動量不確定度,h為普朗克常數
物體運動的速度和位置總是測不準的,兩者的誤差的乘積一定大於一個特定的值。測不準原理是世界的內稟屬性,它來自這個世界的波粒二象性。在理論上,無論採用多麼精準的儀器和手段,測不準原理永遠存在。從測不準原理來看,我們所能瞭解到的物理世界是有限的:總是存在一個固定的限制讓我們不能測出微觀粒子的位置。而“距離”的判斷基礎就是位置,如果粒子的位置有最小的分辨率,那構成世界的粒子就不可能做出比這個分辨率更小的運動距離(因為如果運動距離小於最小距離,人類也無法測量出來,因此這種運動是無法被感知的,也就是不會對人類產生任何影響,因此這種小於分辨率的運動不存在)。這個距離就是解決芝諾問題的關鍵。
小小的黑洞
測不準原理為能夠測量的最小尺度做出了限制,要測得準確的位置信息就必須縮短測量用光子的波長,或者說增大能量。而這個能量的增加是有上限的,上限之一就是施瓦西半徑。假使物體的半徑小於它的施瓦西半徑,物體就將因為密度過大而坍縮為一個黑洞。如果所測量的粒子從光子處獲得的能量太多太多,根據質能方程,物體的質量會隨能量增大而劇增,它本身就會變成黑洞。而光子是無法從黑洞逃逸、返回測量儀器的,因此測量不會得到任何結果。所以施瓦西半徑也是測量物質最小長度的一個限制。
Rs為史瓦西半徑,c為光速,G為萬有引力常數,M為粒子質量
普朗克長度
由以上我們知道,測量長度信息時我們選用的粒子要滿足測不準原理和施瓦西半徑兩個條件。由這兩個條件可以列出以下公式,藉助質量M來求解。
普朗克長度的計算過程
根據測不準原理,微觀粒子的位置存在最小不確定量,就是其運動的最小“分辨長度”。粒子的運動距離小於分辨長度的時候我們就無法分辨運動了,因此這個分辨長度就是我們所求的“世間的最小尺度”。分辨長度和粒子動量的乘積必須大於特定值。為了使分辨長度最小,粒子的動量Δp就要最大,這裡假設為Mc。另一個公式當中,質量為M的粒子有最小的半徑,也設定為分辨長度lp。兩個公式聯立,就得到了宇宙的最小可測尺度:普朗克長度。
因為普朗克長度是可以測量的最小尺度,光速是宇宙中最快的速度。最快的速度走過最小的尺度的時間也就是我們可以測量的最小的時間,即普朗克時間。一普朗克秒約為5.39×10^-44s.
要注意的是,普朗克長度指的是最小的可測量長度,是物理意義上有意義的最小長度。假如說:“我取普朗克長度的一半,不是比普朗克長度更小嗎?”這種假設在思想上是可行的,但是在實際的物理學實踐上是毫無意義的。至於在普朗克長度限制之下的世界是如何運行的,究竟是像動畫一樣逐幀播放、時間空間同時前進,還是粒子以最小單位先進行空間位移再進行時間軸的移動,我們仍然不得而知。
總之,追逐烏龜的阿喀琉斯現在終於可以確定地追上烏龜了,因為他們之間的距離決定對不可能小於一個普朗克長度;莊子的木棒也終於不能再分;現代物理學的極限也到此為止,普朗克長度之下成為了絕對黑暗的領域。但是,就像當年量子力學和相對論拆除了“已經落成的物理學大廈”一樣,沒人有資格斷言在遙遠的未來不會誕生另一種更為精確巧妙、更接近宇宙真理的科學體系。說不定在普朗克長度之下,真的是上帝所處的地方呢?
玻爾說過,“誰要是不對量子力學有疑問,誰就不懂量子力學”。誰也無法篤定量子力學就是揭示宇宙本質的終極工具,也沒人敢說普朗克長度之下的世界人類無法窺探。誰知道在遙遠的未來會發生什麼呢。