世界上最快的运动员,追不上一只普通的乌龟?古希腊“芝诺悖论”因其浅显易懂的描述和颠覆直觉的推论为人所熟知,千百年间受到了广泛的讨论和争议。直到近现代量子力学的研究不断进步,物理界四神兽之一的芝诺乌龟才被彻底打败。本篇文章就带大家讨论一下,物理学究竟如何驳倒了恼人的芝诺悖论。
前车之鉴
人类探索无限小的历史已经不可细考。古印度教的胜论派主张世界由不可分割的极微组合而成;中国《庄子·杂篇》中“一尺之棰,日取其半,万事不竭”的论断则认为不存在最小的不可分割的尺度;古希腊爱丽亚学派的代表人物芝诺多罗斯提出的芝诺悖论思考了时间与空间的分割和连续问题。芝诺悖论中最为有名的阿喀琉斯悖论的主要内容是:喀琉斯是古希腊最有名的运动员,他将和一只起跑时领先他一段路的乌龟赛跑,当阿喀琉斯跑完起跑时二者相差的路径时乌龟也前进了一段距离;当阿喀琉斯再次追完二者相差路程,乌龟就又前进了下一段更小的距离……如此循环,阿喀琉斯只会不断接近但却始终追不上乌龟。
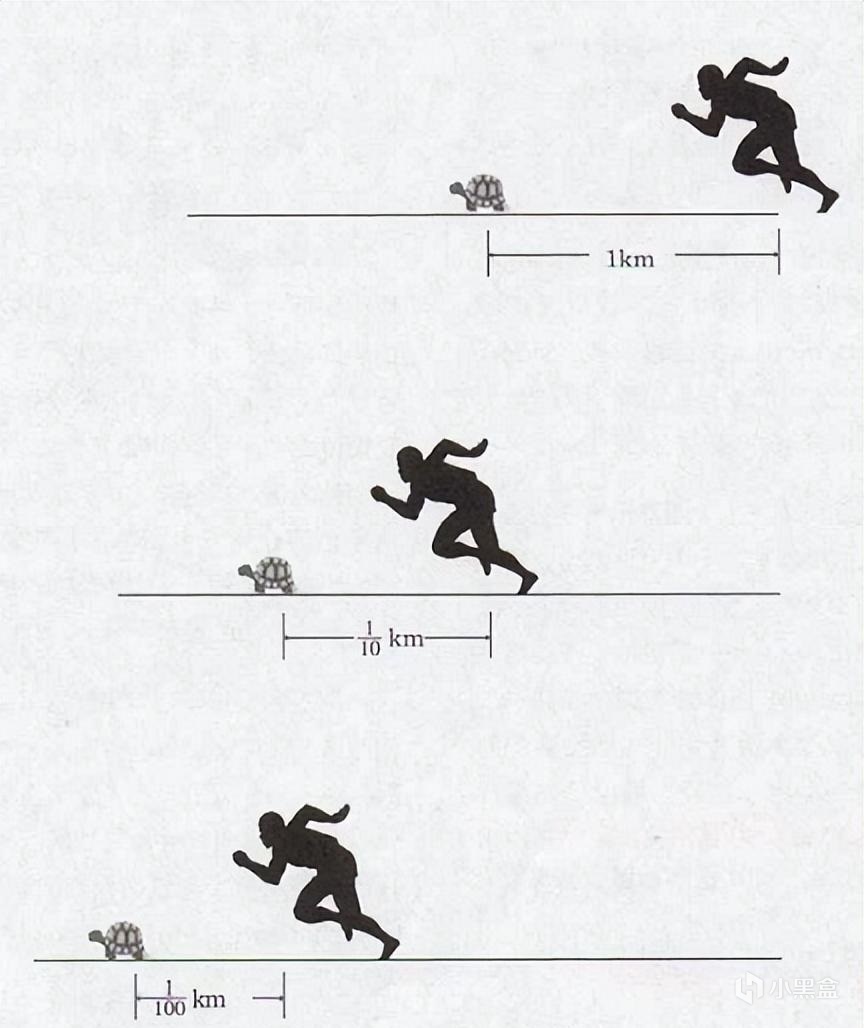
阿喀琉斯永远追不上乌龟
这个看似简单的问题,包含着古希腊哲学家芝诺多罗斯对空间的思考。芝诺是古希腊爱丽亚学派的主要代表人物,主张时间和空间的可微性,即时间和空间都是可以无限进行分割的,并以此否定运动的存在。他所提出的四大悖论以通俗易懂的口吻提出了对于时空的思考。所以乌龟悖论也被称为芝诺第二悖论。如果空间是可以不断分割的,那么阿喀琉斯和乌龟之间的距离就可以无限小,所以阿喀琉斯总是追不上乌龟。假如我们将这个问题反过来看,回到阿喀琉斯刚刚起跑迈出第一步的时候:阿喀琉斯要先把脚迈出1厘米,就必须先跨出0.5厘米;要跨出0.5厘米,就必须先跨出0.25厘米……如此持续地分下去,阿喀琉斯必须要经过无限个流程才能开始运动,因此阿喀琉斯永远也不可能运动。芝诺就是用这样简单易懂的问题,表达了自己“时空可微、运动不存”的观点。
阿喀琉斯追不上乌龟的答案显然是错误的,如果真的如此,在另一个故事里即便兔子睡得时间再长,乌龟也不可能取胜。那问题的真相是什么呢?有一个有趣的说法是,因为阿喀琉斯总是追随着乌龟的脚步,所以永远也不可能超越乌龟。这个回答显然足以对悖论做出字面的解释。但我们必须知道包括芝诺的乌龟在内的物理学四大神兽,都只是更深刻的物理问题的抽象表达,只是物理学家为了更加生动地描述物理问题而讲的童话故事。要真正打败芝诺的乌龟,必须从问题的初衷入手:空间本身可以被无限细分吗?
测不准和绝对的小
迈克尔·菲尔在著作《啤酒与肥皂》中称量子力学为“研究绝对的小的物理学”。我们知道在经典物理学中,只要采取正确的测量手段就不会对测量对象造成影响。比如测量一辆车的位置和速度(或者说动量),只要用合适的器具正确测量,车的位置和速度总是确定的,不会因为测量的行为而改变。但是在量子力学的领域中,测量的对象是“绝对小的东西”。什么是绝对小的东西?比如要测量一个电子的位置和动量,我们总是需要用其他的微观粒子来碰撞这个电子,然后观察粒子在碰撞前后的变化来判断电子的状态。但是对于电子这样小的粒子来说,要准确测量位置就必须选用波长足够短的光子才能测得更为精确;而光子波长越短能量越大,碰撞中对电子速度的影响也会越大,于是就无法准确测量电子的动量。如此以至于测量的动作改变了每一个被测量的电子的状态从而产生了不可忽略的偏差,这时就可以说我们测量的对象是绝对小的东西,所做的研究也就归属量子力学。而所谓“不可忽略的偏差”的存在,被人们称为“测不准原理”。
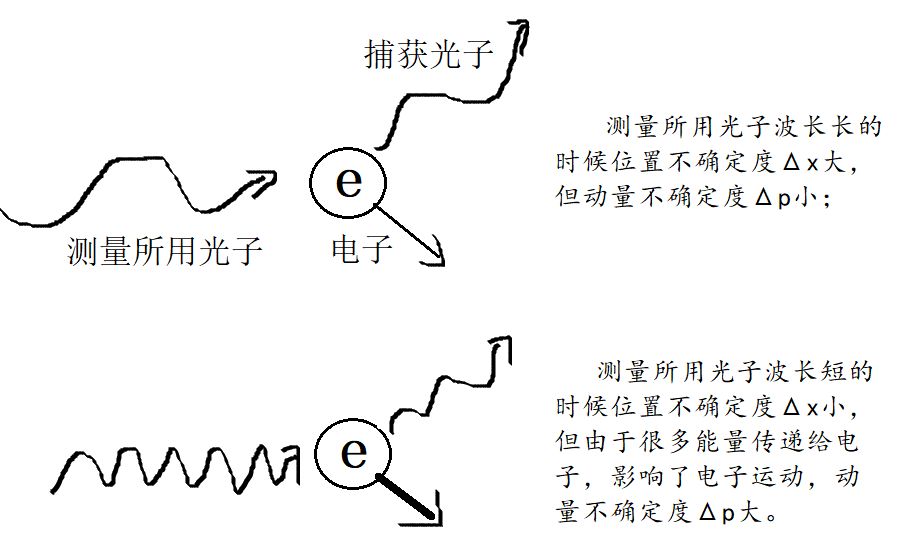
测量的动作会影响测量的结果
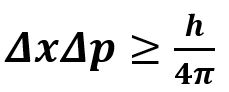
Δx为位置不确定度,Δp为动量不确定度,h为普朗克常数
物体运动的速度和位置总是测不准的,两者的误差的乘积一定大于一个特定的值。测不准原理是世界的内禀属性,它来自这个世界的波粒二象性。在理论上,无论采用多么精准的仪器和手段,测不准原理永远存在。从测不准原理来看,我们所能了解到的物理世界是有限的:总是存在一个固定的限制让我们不能测出微观粒子的位置。而“距离”的判断基础就是位置,如果粒子的位置有最小的分辨率,那构成世界的粒子就不可能做出比这个分辨率更小的运动距离(因为如果运动距离小于最小距离,人类也无法测量出来,因此这种运动是无法被感知的,也就是不会对人类产生任何影响,因此这种小于分辨率的运动不存在)。这个距离就是解决芝诺问题的关键。
小小的黑洞
测不准原理为能够测量的最小尺度做出了限制,要测得准确的位置信息就必须缩短测量用光子的波长,或者说增大能量。而这个能量的增加是有上限的,上限之一就是施瓦西半径。假使物体的半径小于它的施瓦西半径,物体就将因为密度过大而坍缩为一个黑洞。如果所测量的粒子从光子处获得的能量太多太多,根据质能方程,物体的质量会随能量增大而剧增,它本身就会变成黑洞。而光子是无法从黑洞逃逸、返回测量仪器的,因此测量不会得到任何结果。所以施瓦西半径也是测量物质最小长度的一个限制。
Rs为史瓦西半径,c为光速,G为万有引力常数,M为粒子质量
普朗克长度
由以上我们知道,测量长度信息时我们选用的粒子要满足测不准原理和施瓦西半径两个条件。由这两个条件可以列出以下公式,借助质量M来求解。
普朗克长度的计算过程
根据测不准原理,微观粒子的位置存在最小不确定量,就是其运动的最小“分辨长度”。粒子的运动距离小于分辨长度的时候我们就无法分辨运动了,因此这个分辨长度就是我们所求的“世间的最小尺度”。分辨长度和粒子动量的乘积必须大于特定值。为了使分辨长度最小,粒子的动量Δp就要最大,这里假设为Mc。另一个公式当中,质量为M的粒子有最小的半径,也设定为分辨长度lp。两个公式联立,就得到了宇宙的最小可测尺度:普朗克长度。
因为普朗克长度是可以测量的最小尺度,光速是宇宙中最快的速度。最快的速度走过最小的尺度的时间也就是我们可以测量的最小的时间,即普朗克时间。一普朗克秒约为5.39×10^-44s.
要注意的是,普朗克长度指的是最小的可测量长度,是物理意义上有意义的最小长度。假如说:“我取普朗克长度的一半,不是比普朗克长度更小吗?”这种假设在思想上是可行的,但是在实际的物理学实践上是毫无意义的。至于在普朗克长度限制之下的世界是如何运行的,究竟是像动画一样逐帧播放、时间空间同时前进,还是粒子以最小单位先进行空间位移再进行时间轴的移动,我们仍然不得而知。
总之,追逐乌龟的阿喀琉斯现在终于可以确定地追上乌龟了,因为他们之间的距离决定对不可能小于一个普朗克长度;庄子的木棒也终于不能再分;现代物理学的极限也到此为止,普朗克长度之下成为了绝对黑暗的领域。但是,就像当年量子力学和相对论拆除了“已经落成的物理学大厦”一样,没人有资格断言在遥远的未来不会诞生另一种更为精确巧妙、更接近宇宙真理的科学体系。说不定在普朗克长度之下,真的是上帝所处的地方呢?
玻尔说过,“谁要是不对量子力学有疑问,谁就不懂量子力学”。谁也无法笃定量子力学就是揭示宇宙本质的终极工具,也没人敢说普朗克长度之下的世界人类无法窥探。谁知道在遥远的未来会发生什么呢。