第三章 複雜系統與突現結構
在前兩章中,書中重點解釋了遊戲可玩性是如何從遊戲機制中產生的,同時說明了突現型遊戲的機制具有一種特定結構,在這種結構下,用一些較為簡單的規則就可以產生出多種多樣的可玩性。一般來說,這也意味著突現型遊戲有很高的重玩價值。而在本章中,則會更詳細地探討突現、遊戲機制的結構和遊戲可玩性這三者的關係。
突現性-可玩性?
可玩性(gameplay)這個詞被定義為遊戲給予玩家的各種挑戰,以及玩家在遊戲中所能執行的行動。多數行為/功能能夠幫助玩家克服挑戰並且由遊戲機制所控制,但也有一些行為(例如更換賽車的顏色或與其他玩家聊天)與挑戰無關。
當然,如果要把遊戲設計成每個挑戰只能通過一種獨一無二的活動來解決是完全可能的,比如各類文字遊戲。舉個筆者自己的例子,在今年的CGJ上做出來的惡搞解謎小遊戲就是一種關卡與關卡之間機制、交互完全獨立的設計:
鏈接: GmHub,有安卓和windows的包。
不過大部分遊戲應當都有一個或多個核心的機制與玩法來構建gameplay本身, 比如俄羅斯方塊、三消遊戲等,雖然可以通過程序實現不同色塊的生成和掉落規則以保持遊戲本身的有趣性與平衡性,但是這種基於玩家動作產生的隨機結果依舊是不可預測的, 這種結合的方式每次都不同,並且玩家對他們所面對的挑戰具有一定的控制力。這個遊戲可產生的挑戰變化是無窮無盡的,但玩家只需用很少的幾種操作就足以應付它們。
遊戲的一致性應當高於其寫實性。
這句話是Steven Poole 在《Trigger Happy》(2000)一書中提出的觀點:遊戲的一致性比寫實性更重要。Poole認為,玩遊戲是一種玩家讓自己沉浸在遊戲機制構築的模擬世界中的活動。玩家並不希望遊戲機制分毫不差地模擬現實。例如,一個完全寫實的、要求玩家必須花費長達數年時間練習,才能掌握足夠技巧從而上場比賽的F1賽車遊戲,對於大多數玩家來說根本不會有趣。 學習成本遠高於獲得快感的成本,這類更像是模擬器的遊戲比如Xplane、truck simulator等遊戲應當劃分在Serious Game的領域中,即一種出於學習目的的,有實際應用意義的遊戲類型。

此類遊戲的第一目的是“擬真”、“學習”而非遊戲性本身。
回到突現性遊戲本身,之前說到突現型遊戲有很高的重玩價值,是因為玩家每次玩遊戲時遇到的挑戰和可能作出的對應行為都不相同。遊戲的每一段時期都是玩家與遊戲的交互與影響而產生獨一無二的結果。然而,僅僅通過觀察規則很難預測出某個遊戲是否會生髮出有趣的可玩性。我們在上一章中討論井字棋和屏風式四子棋時已經說明過,創造突現型因素並非靠規則的堆砌。規則的複雜度和遊戲所表現出來的複雜度不是線性關係而是一種爆炸式的指數關係(當然也取決於規則本身之間的相互影響程度),並且規則越多並不意味著遊戲越有趣。事實上,如果將規則的數量減少,有時更容易創造出一個能產生真正有趣和突現型的可玩性的系統。
混沌與秩序
許多遊戲的複雜系統(表現為極多個簡單機制的糅合構成的複雜系統,如《文明》系列)的行為與表現是會受到“混沌”和“秩序”的影響的,放在今天更為通俗的說法就是隨機性與玩家可控性的權衡,比如在諸多有季節更替和天氣的遊戲中,既有可以表現為“混沌”的天氣系統,也有表現為“秩序”的季節變化。(在《GTA5》中,每年遊戲在聖誕節時候就會把天氣變為雪天,而其他時候大部分天氣都是隨機的,當然現在雪天也已經加入了隨機天氣全家桶中。)

而在秩序和混沌這兩極之間,還有兩個階段:週期性系統和突現性系統。
此處我們仍舊以天氣變化為例:
週期性系統在運行過程中會以一個連續且易於預測的次序經歷若干個區分明確的階段。在較大的規模上,天氣系統和季節交替現象就是以這種方式運行。你在地球上的位置決定了你每年會經歷哪幾個季節。在一些地區,季節輪轉的節奏非常精確,每個季節在一年中到來的日期幾乎是固定的。儘管氣溫會產生季節性變化,季節開始的日期每年也有所差異,但天氣系統大體上是平衡的,並以固定的循環一遍又一遍地輪迴。
與週期性系統相比,突現性系統的有序程度較低而混沌程度較高。突現性系統的行為模式通常比較穩定,但也可能會毫無徵兆地突然從一個模式轉變到另一個模式。天氣系統就是一個好例子。雖然某一特定地域的季節循環是遵循著一個大體規律的,但要預測某一年的天氣情況仍然很困難。由於氣壓、海水溫度和大氣溫度之間有著複雜的相互作用,要準確預測下一次出現霜凍的日期或整個冬天的降雪量幾乎是不可能的。
大部分的漸進型遊戲都以有序性系統為主,設計師可以通過玩家在遊戲的各種行為去預測下一步發生了什麼,玩家的各種行為也產生了一個週期性系統,但具有更多的細微變化性。在大多數MMORPG中,離散性的時間單元機制影響著玩家所採取的策略。在《文明》中,各個明確區分開來的發展階段(擴張、合併、戰爭、殖民、太空競賽)則是遊戲中的突現行為的清晰體現。
那麼此處便涉及到了一個很重要的問題,遊戲中的突現現象是否可以人為設計?
本章的後續內容都基於這一問題展開,複雜系統中的突現現象只有當系統實際開始運轉後才會顯現出來,這解釋了為何遊戲設計如此依賴原型構建和遊戲測試。 下面一些例子是書中提出的在遊戲之外的複雜科學,這些理論雖然看上去與遊戲沒有直接關係,但是還是有不少應用價值。
複雜系統的結構特性
複雜科學的研究對象通常涉及規模龐大的複雜系統,天氣系統就是一個經典例子。在這些系統中,一個小小的變化就可能隨時間推移而造成巨大的影響,也就是所謂的蝴蝶效應。
複雜系統的案例-細胞自動機
在數學、計算機科學和遊戲理論的交界處,有一個特殊的學術領域,它研究的對象是細胞自動機。細胞自動機是一系列簡單規則的集合,這些規則控制著一行格子或一個網格中的每個格子單元所呈現出的狀態。每個格子只有兩種狀態:黑色或白色。規則決定了格子顏色改變的條件,以及當前格子顏色如何對周圍的格子產生影響。如要根據規則改變格子顏色的話,在二維網格中通常只需檢測當前格和周圍八個鄰接格的顏色。在一維網格(單行格子)中,通常只需檢測當前格和兩個鄰接格的顏色。
數學家們把這樣的一個規則集合看作一種假想的機器,這種機器無需人工干預就能自行運轉,只需要輸入規則和一個初始狀態即可。這也是它被稱作自動機的原因。儘管很多細胞自動機的規則沒有任何隨機性,但它卻能產生出獨特且看似隨機的圖形。

一種細胞自動機的設計結果,下方是格子之間相互生成的規則
細胞自動機的背後實際上是一套動態行為系統,這類系統有三個關鍵特性:
- 系統必須由簡單的單元(cells)構成,這些單元的規則必須是局部性的。
- 系統必須支持遠程信息傳遞。複雜系統中的某一個組成部分狀態的改變必須要能跨越較遠的時間或距離,造成系統其他組成部分的改變。
- 系統組成單元的活躍程度能夠有效地反映出系統行為的複雜度。如果一個系統中的活躍單元很少,那麼它就不太可能生髮出複雜的行為。
所以讓我們回到遊戲本身,構建動態行為系統的門檻其實出乎意料的低。只要有足夠多的組成部分以及足夠高的活躍性和關聯性,那麼相對簡單的規則也能產生出複雜的行為。大多數遊戲都是通過與之類似的方式構建出來的。遊戲由許多不同的元素組成,這些元素由相當簡單的機制控制著,各元素之間通常存在著很多互動作用。
比如塔防類型的遊戲,單個的防守機關都是由局部規則所定義的, 和細胞自動機一樣,這些元素既具有活躍性(敵人會進行移動,塔會對敵人作出反應),也具有相互關聯性(有的塔會攻擊敵人,有的塔能提升周圍其他塔的威力,或者對敵人造成debuff等)。
系統元素的活躍度和相互關聯度是很好的指示器,可用於將突現型遊戲和漸進型遊戲區分開來。在典型的漸進型遊戲中,所有元素(例如謎題和角色等)都只與玩家控制的角色相交互,而且它們僅在玩家可見時才表現出活躍性——此前大部分遊戲中的NPC,只會對玩家或玩家產生的行為做出反應而不受其他任何元素的影響,但是當今也不乏許多設計優秀的遊戲,將遊戲對象的感知行為擴張到更多的元素,比如荒野大鏢客中會躲雨的NPC,老頭環中不同陣營會相互打架的敵人等等。

反饋循環對系統的影響
反饋循環即當前的系統狀態與結果去影響系統下一步規則或發展趨勢產生動態變化的行為。以生態系統中生物與天敵的關係為例,當獵物很多時,捕食者很容易得到食物,它們的數量因而上升。然而,隨著捕食者越來越多,獵物會不斷減少。當捕食者數量增長到一定程度後,情況便發生了逆轉:捕食者因得不到足夠食物而數量下降,給了獵物生存繁衍的機會,使獵物數量重新上升。此類維持系統平衡的反饋循環叫做負反饋循環。這種循環在生活中有著廣泛應用,恆溫器就是一個典型例子。恆溫器會檢測空氣溫度,當溫度過低時,激活加熱裝置使室溫上升,當檢測到室溫高於一定值後,又會反過來關閉加熱裝置。
再回到遊戲中,負反饋循環也在遊戲進行平衡設計中有著非常多的應用,比如最近版本的英雄聯盟中推出的“戰略點”機制以及很早就存在的賞金機制,劣勢方的玩家拿下戰略點或對方優勢角色的擊殺之後會獲得額外的金幣獎勵,而這一獎勵對於優勢方是沒有的。

與負反饋相反,正反饋循環也同樣廣泛存在於遊戲之中, 負反饋循環的自身反饋效應能維持平衡,而正反饋循環的自身反饋效應卻會使效果加強。
依舊以MOBA類遊戲為例,擊殺敵人本身也為團隊取得了戰術、經濟上的諸多優勢,變得更容易取勝,比如很多FPS遊戲中的連續殺敵獎勵等。
另一種細胞自動機:《生命遊戲》
回到理論本身,最著名的細胞自動機大概是由John Conway 發明的《生命遊戲》 。
此處直接放上鍊接: Play John Conway’s Game of Life (playgameoflife.com)
與前面的自動機類似,《生命遊戲》是基於一個無限大的2D網格,每個格子有“活躍”和“死亡”兩種狀態(也就是黑和白),在大多數例子中,死亡的細胞格被標記為白色,存活的細胞格被標記為黑色。系統在每次迭代時執行以下規則:
- 如果一個存活的細胞格周圍存活的鄰格少於兩個,則此格由於過於孤獨而死去。
- 如果一個存活的細胞格周圍存活的鄰格多於三個,則此格由於過度擁擠而死去。
- 如果一個存活的細胞格周圍存活的鄰格為兩個或三個,則此格保持存活狀態。
- 如果一個死亡的細胞格周圍存活的鄰格恰好為三個,則此格死而復生。
《生命遊戲》在開始運行後,通常會以初始存活的細胞格為源頭引發大量細胞格的爆發式活動,產生混沌性相當高的結果。《生命遊戲》通常在若干次循環後進入大體穩定的狀態,但有時候仍會餘下若干群細胞格在兩個狀態之間不斷振盪。
而《生命遊戲》的精髓在於,通過這些規則與初始狀態的設定,可以取得許多具有特定功能或行為的組合式單元,比如:
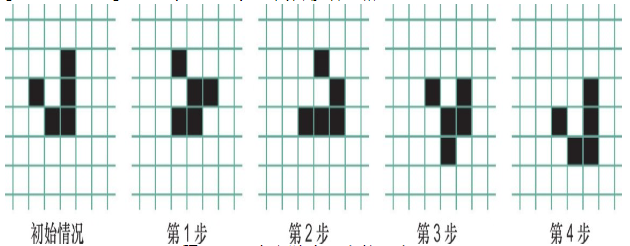
每一輪變化會向固定方向前進一格的“細胞單位”
此類例子說明,在複雜系統中,最有趣的行為不是在系統的個體組成部分這個規模級別上產生的,而是在由許多個體部分所組成的群體這個規模級別上產生的。
而在遊戲中,許多AI的行為設計也是通過此類組合行為顯得非常“智能”,書中給出的例子是在吃豆人遊戲中,不同的AI會收到不同的追捕指令類型,從而始終造成一種對玩家圍追堵截的“戰術”表象。
突現性的等級劃分
科學家們將複雜系統中的突現劃分為不同等級,某些現象的突現性等級比其他現象要高。將複雜系統中的反饋循環和規模級別這兩個概念結合起來,可以幫助我們描述並解釋突現特性的不同等級。科學家Jochen Fromm 在論文《Types and Forms of Emergence》中以反饋和規模級別為標準,對突現進行了如下分類:
最簡單的突現被稱為微小突現或有意突現,它們要麼不存在反饋,要麼反饋只發生在同一規模級別中的各個元素之間。大多數人造機器設備都屬於這類系統,這些機器所展現出來的功能是設計者通過設計,有意使機器各部件產生出的突現特性。展現出這種有意突現的機器,其行為是確定性的、可預測的,但也缺少了靈活性和適應性。調速器和恆溫器就是這種可預測反饋的例子。
第二種類別是弱突現,這種突現類型可以在系統的不同層級之間實現自頂向下的反饋。比如在各種生物集群中。生物個體不僅會對周圍其他個體的行為作出反應(中介體到中介體的反饋),同時也會感知到集群這個整體(群體到中介體的反饋)。
第三種是多重突現,這種系統中具有多種反饋,這些反饋跨越了不同的規模級別。為了解釋這種突現類型,作者闡述了此類突現是如何在那些具有小範圍正反饋和大範圍負反饋的系統中得到體現的:
股市就表現出這種特性。當股價上漲時,人們會注意到併購買更多股票,導致股價繼續升高(短期正反饋)。同時人們根據經驗知道股價總有一刻會達到頂峰,因此他們會適時賣出股票,導致股價下降(長期負反饋)。這種現象反過來也成立,人們發現股價下跌時會賣出股票,但當他們認為股價已經到底時,又會抱著佔便宜的心理重新買入。
最後一種則是強突現, 強突現的產生應歸因於各規模級別間的較大差異,以及系統中的中間規模級別的存在。強突現是多層級的突現,其中最高層級所產生的突現行為可與最低層級上的中介體分離開來。 比如基因系統發生突現而產生生命,或者語言和書寫發生突現而產生文化。
以上這些突現類型說明不同層級的突現行為在遊戲中是同樣存在且常常是並存關係。更重要的是,遊戲機制的結構特性(例如規模層級的存在以及反饋循環)對於複雜和有趣的行為特性的生髮起著至關重要的作用。
如何在遊戲中控制突現特性?
遊戲屬於複雜系統,能夠產生出不可預測的結果,但同時也必須為玩家帶來設計良好、自然合理的用戶體驗。
我們把以上所學的活躍並相互關聯的系統組成部分、反饋循環、系統的不同規模級別等概念看 作一個系統,這就是遊戲的結構特性。
後續所有章節都會圍繞著遊戲機制與結構特性進行展開,也就有了更多更為具體的理論與配套的遊戲案例,這些結構特性既是本章的主題,也是理解Machinations構造原理的前提知識。(Machinations是一個實用性的理論框架,它可以直觀地處理遊戲中的突現特性。一個表現出突現特性的高質量遊戲的構建過程是難以掌控、捉摸不定的,而Machinations能使設計師更好地掌控這個過程。)
這一工具在首篇的開頭便已經提出:讀書札記丨《高級遊戲設計技術》其一
在接下來的幾章中,書中會把視角拉近到遊戲的內部經濟機制上。將闡述如何用Machinations將遊戲機制可視化,以及如何利用這些可視化成果來認識機制的結構特性等問題。