前言
在上一篇中我們進行了三維重構方面的簡單介紹,並很快引入了第一步的主題——立體視覺。這次繼續讀斯坦福大學的這篇課件。
PPT部分以翻譯為主,打星號的部分是我的個人理解或補充,主要是對課件中沒解說的部分補充外部信息。
一、解決對應點問題——Solving the correspondence problem
*這部分課件中舉例用的一些圖都不算直觀,有點難以看出左右兩圖的區別。
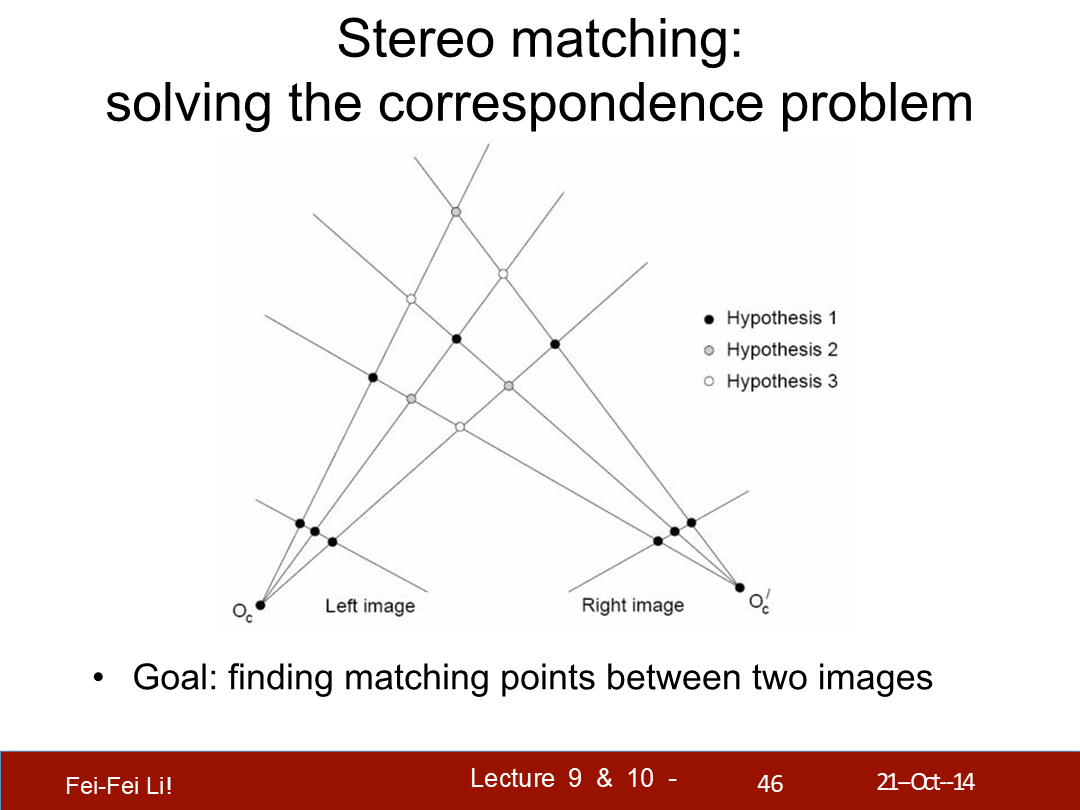
立體匹配:解決對應點問題
目標:找到兩張圖片中的對應點。(*Hypothesis,假設)

基礎的立體匹配算法
對於第一張圖中的每個像素:
- 找到右側圖中的對應極線
- 檢測極線上的每個像素並選擇最匹配的
- 三角測量匹配點以得到深度信息
最簡單的情況——極線都是掃描線(與畫面平行)。何時會發生這種情況?
*選擇匹配點規則後面頁會介紹到。另外,三角測量的方式在上一篇中介紹過了。

如果需要,可以將兩張立體圖片校正以變換極線為掃描線。(變成平行平面)
對於第一張圖中的每個像素x:
- 找到右圖中相對應的極線掃描線
- 檢測極線上的每個像素並選擇最匹配的x'
- 計算差異度x-x',將深度設為它的反比(如圖)

對應點問題
讓我們做一些假設來簡化匹配問題:
- 基線相對很小(和場景中點的深度對比而言)
- 這樣大部分場景中的點都能在兩個視圖中可見
- 並且,匹配的區域在外觀上是相似的

通過相似性約束來查詢對應點
沿著右側的掃描線滑動一個(檢測)窗口,並比較左側中相關聯窗口的結果。
匹配開銷:SSD(後一頁提到了,差方和)或歸一化相關係數。
*兩者都是統計學上量化數據的方式。
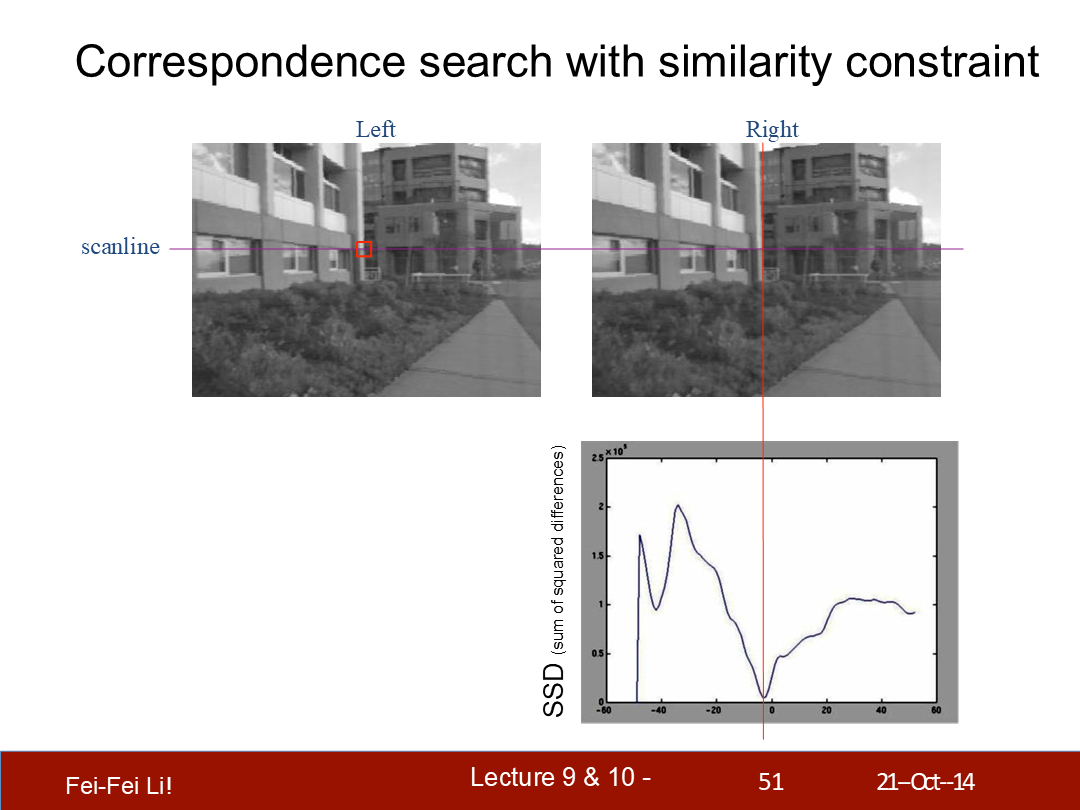
*這裡橫軸是差異度(disparity),縱軸是差方和(Sum of Squared Differences)。這裡對比的是左側的一個位置和右側一條線上的窗口——可以看到圖中的例子中最匹配的點肯定不是差異度為0的,而是接近0。

這裡是一段偽代碼示例,長寬對應一個檢測窗口的尺寸
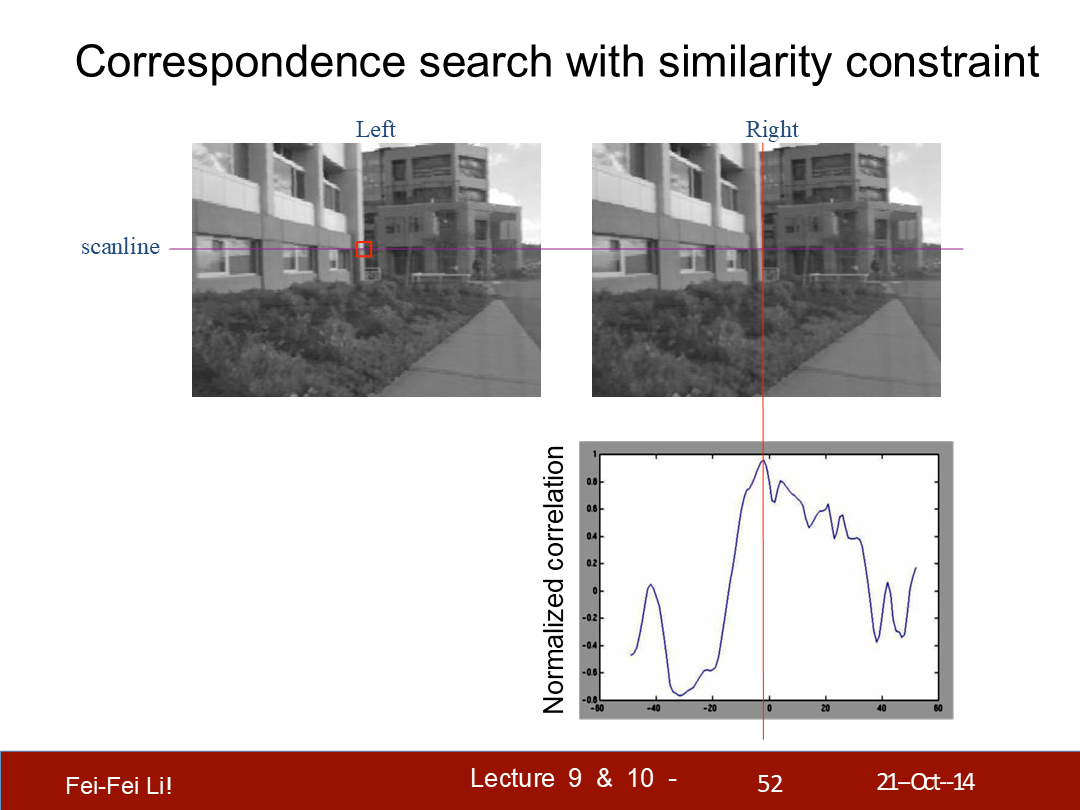
*這裡縱軸換成了歸一化相關係數。不管哪種計算方式,都是對比的窗口像素差異。
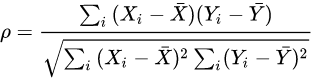
歸一化相關係數的定義。可以看出相似度越高越接近1。

(不同)窗口尺寸的效果
- 小窗口:更多細節,更多噪聲。
- 大窗口:更平滑的差異圖,更少噪聲。
*這裡是差異圖可視化之後的結果,而能表現為灰度圖應該是使用的歸一化相關係數作為顏色顯示,並且處理完整張圖像的結果。

相似性約束
- 兩張圖中對應的區域應該在外觀上類似
- 而不對應的區域應該在外觀上不同
- 那麼何時這一相似性約束會失效?

相似性約束的侷限
(圖中順序依次是):無紋理的表面、剔除或重複、高光表面。

窗口查找的結果
*圖中左側是基於窗口的匹配結果,右側是事實結果(很多算法實驗都會配Ground truth結果作比較)。顏色圖展示的是基於還原深度信息的物體輪廓。

*這裡指出了基於圖切割算法能有更好的結果。其中涉及了用圖論思想優化圖像劃分,後續這個脈絡的算法都被稱為min-cut/max-flow算法。
*之前基於窗口的算法是一種局部算法,而圖切割算法是一種全局算法。
*圖論的部分超出我個人能解釋的能力範圍了,文末會給出2001年這篇論文的鏈接。

基線的作用
- 小的基線:較大深度誤差。
- 大的基線:產生難以查詢的問題。
*圖中反映了兩種情況,通過藍色和紅色包圍的區域表示。不過左側的示意圖並沒有表現出小的基線相對大的基線能更確定點的位置,實際上兩者的觀察點距離應該是差距很大的。
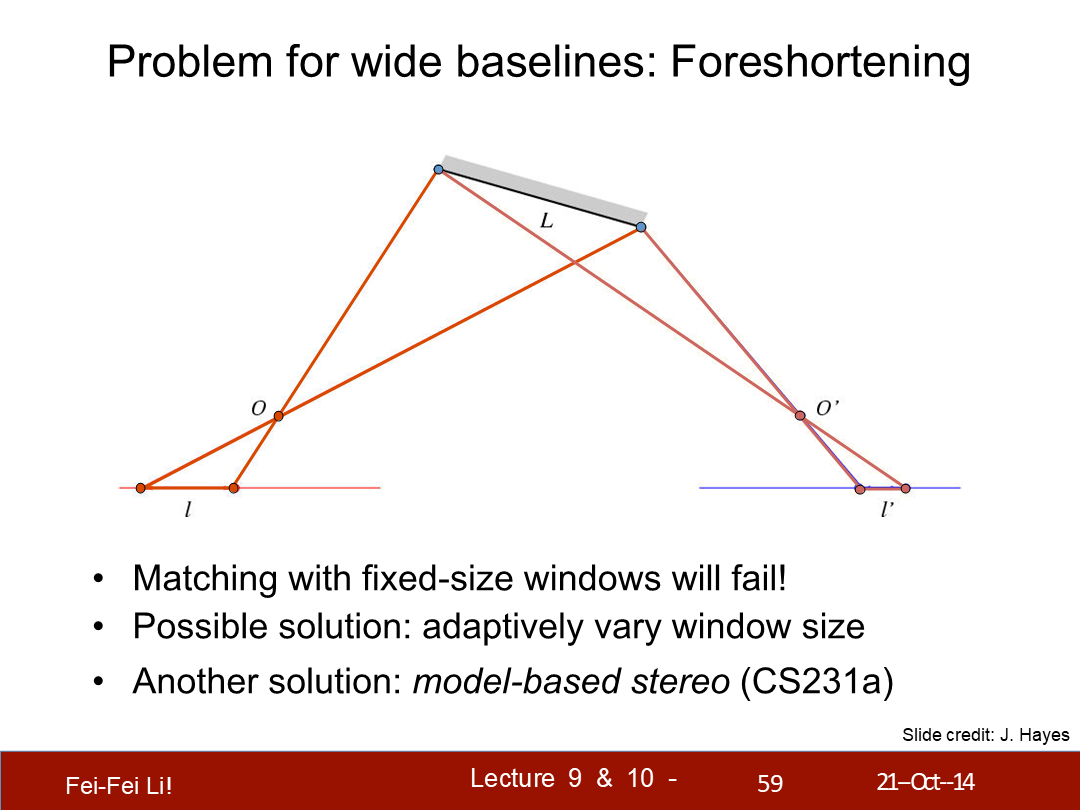
寬基線的問題(的解決):透視法縮繪
- (寬基線的情況)按固定尺寸的窗口匹配將失敗。
- 可行的解決方案:自適應的窗口尺寸。
- 另一個解法:基於模型的立體查詢。
*這裡的model-based指先生成近似模型,再輔助計算點的相關性,這裡摘錄了1996年的一篇論文中提出的概念:
Model-based stereo differs from traditional stereo in that it measures how the actual scene deviates from the approximate model, rather than trying to measure the structure of the scene without any prior information. The model serves to place the images into a common frame of reference that makes the stereo correspondence possible even for images taken from relatively far apart.
譯:Model-based的立體查詢與傳統立體查詢的不同是,它通過與近似模型的偏差來度量(估算)實際場景,而不是嘗試在沒有任何前置信息的前提下來度量場景的結構。這一模型能提供特定幀(觀察位置)的參照,使立體相關匹配變得可行——即使是從相當遠的觀察距離。
*這裡的近似模型生成是從其它的一些參照方式(例如平面識別等)來構建,並輔助提高相關點匹配的準確性。雖然這篇課件主要介紹的是點與點之間的對應算法,但上一篇中介紹的各種方式(紋理、明暗等)都能輔助立體視覺的匹配過程。
二、單應變換——Homographic transformation

回顧:2D中的變換
*(只在平面上的)特定情況中,二維變換矩陣是2X2的,其中R代表旋轉,t代表平移。
*它有著3的自由度(DOF,上篇中介紹過這個概念);能保持距離(區域);剛性物體間符合動量約束。

*普適的情況中,變換矩陣如圖所示(a1-a9)。
*它有著8的自由度,保持共線性的特徵。
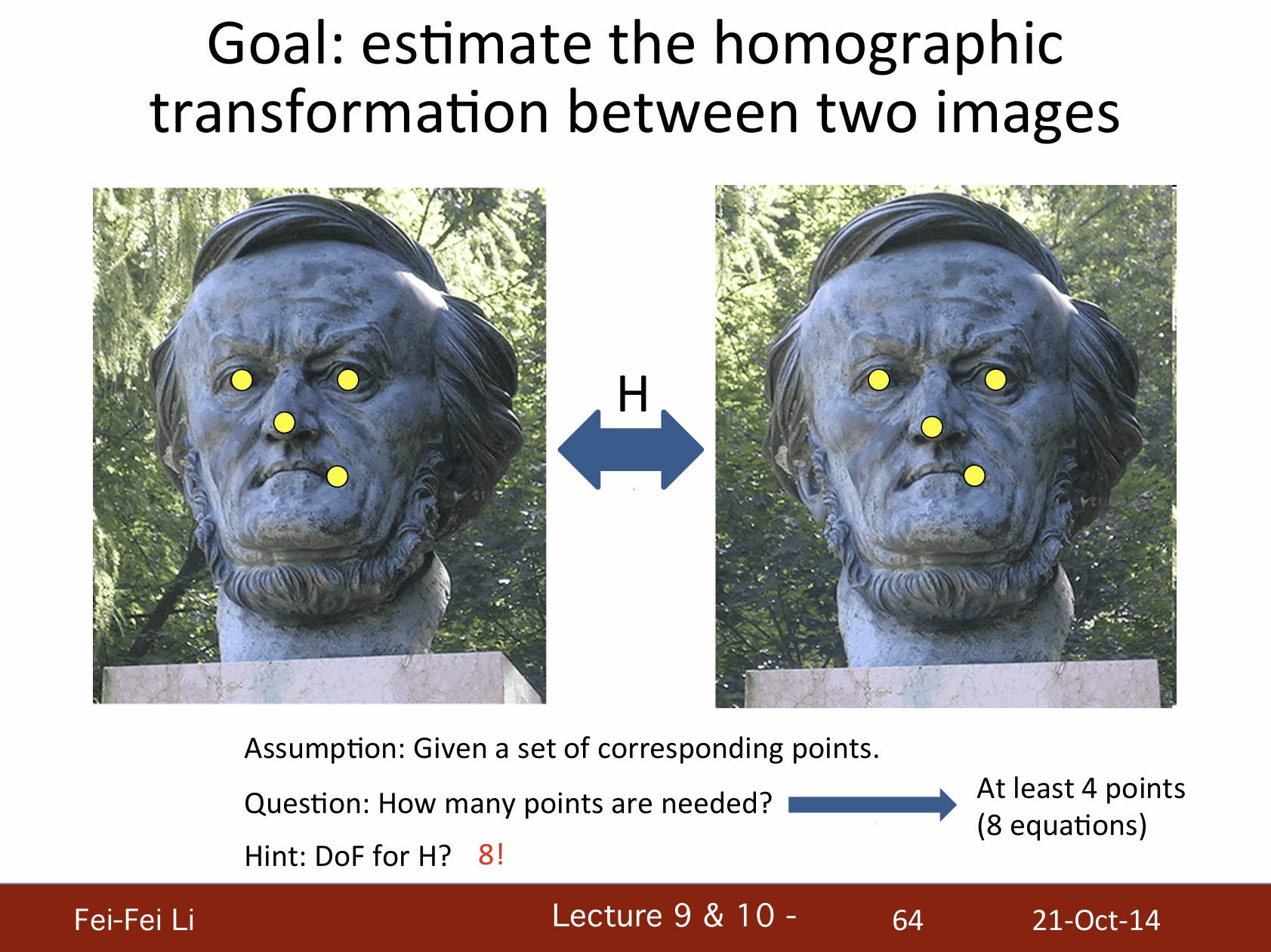
目標:估算兩張圖像之間的單應變換
- 假設:給定一組對應點。
- 問題:需要多少點?——至少需要4個點(8個方程)。
- 提示:變換矩陣H的自由度是8。

DLT算法(直接線性變換)
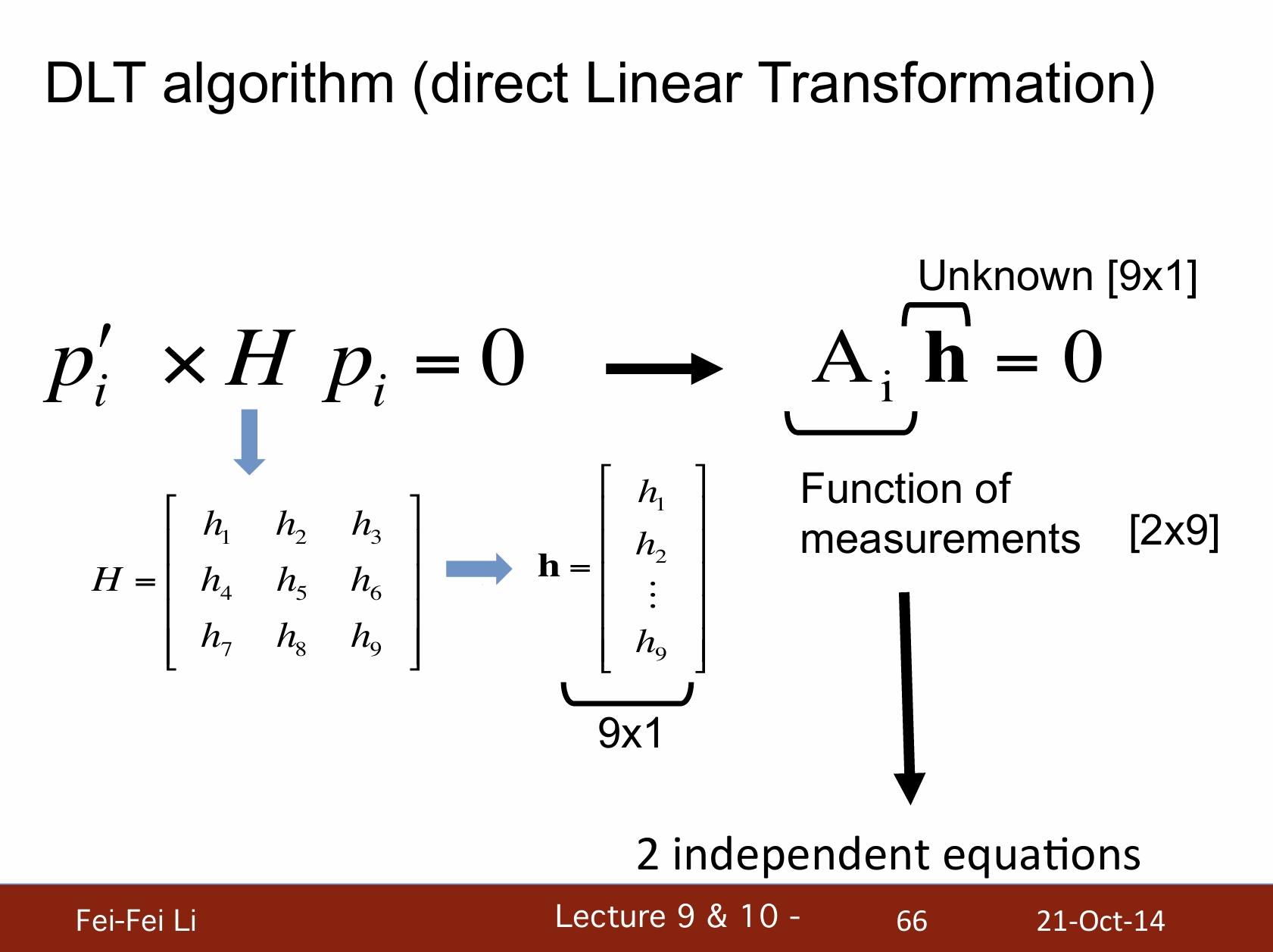
*DLT算法的目的是在已知對應點的情況下,通過建立線性方程組來求解攝像機的投影矩陣。
*這個課件的推導過程缺一點關鍵過程,下面通過資料介紹另一種推導方式:

*最上方的公式相當於pi'=H pi,展成三維座標(向量)的形式。
*中間英文部分就不逐句翻譯了,大致是在講將矩陣乘開成方程組的形式,之後通過相除消去係數a的影響。
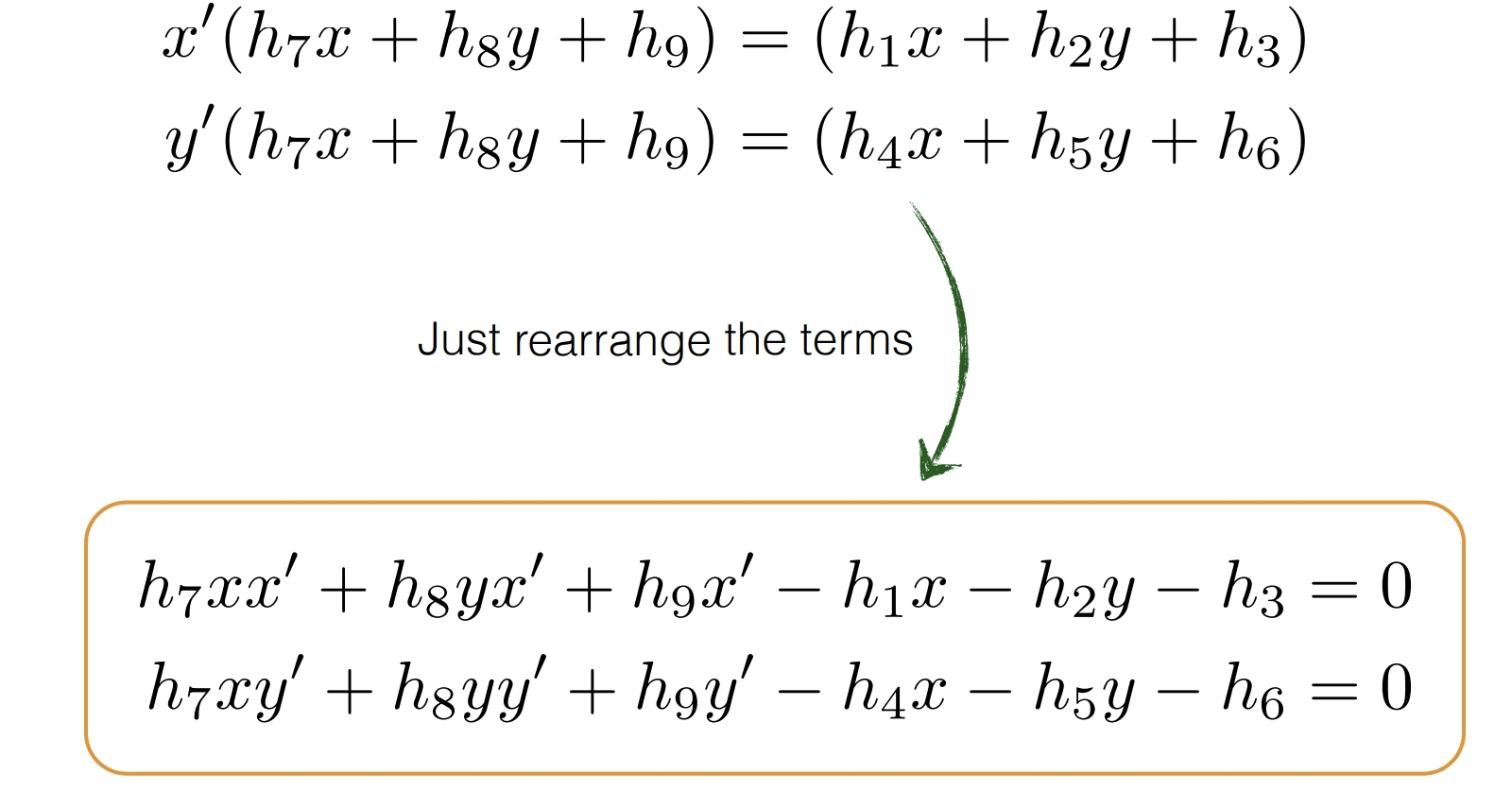
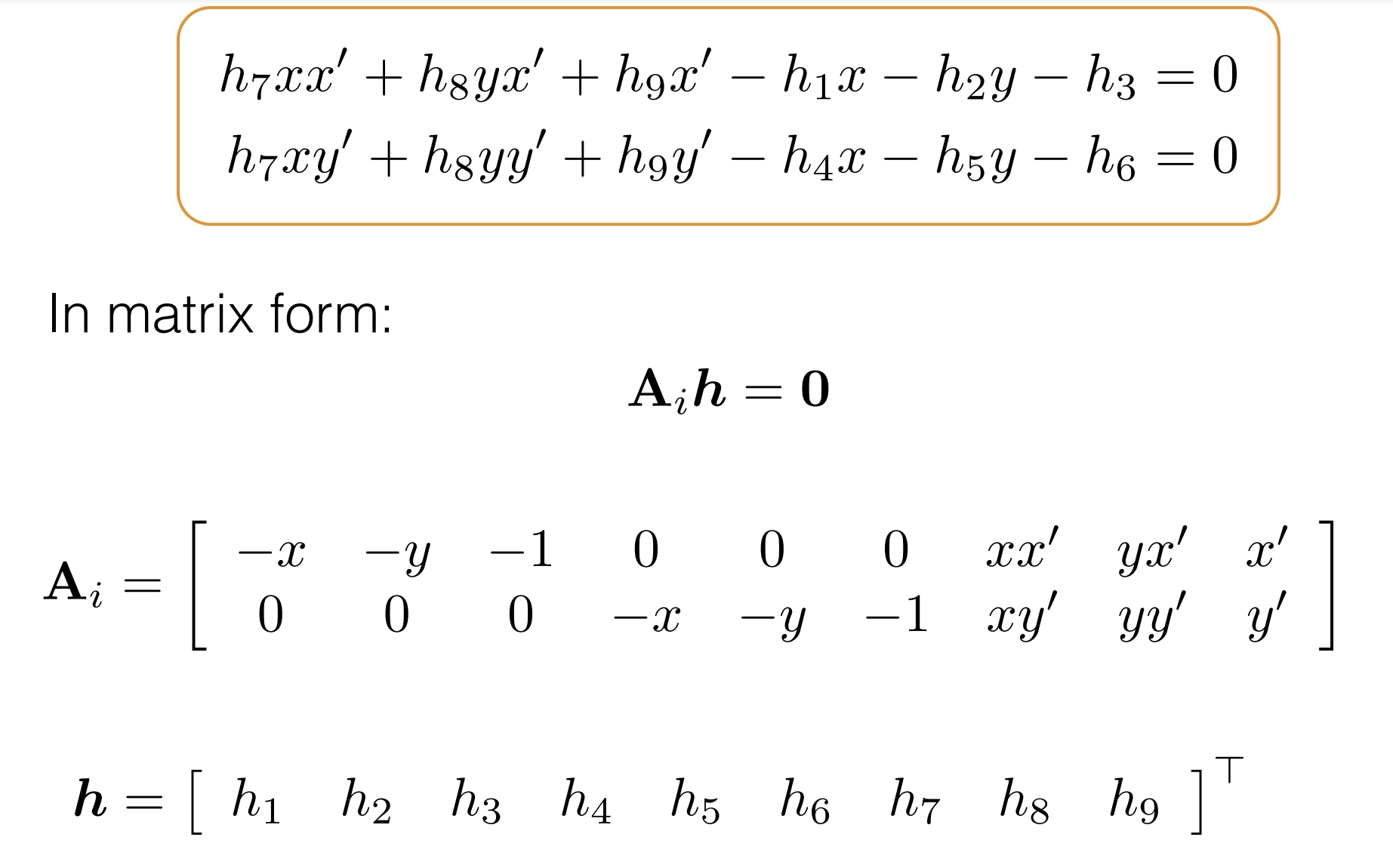
*將項重新排列並寫成矩陣的形式,就和課件中一致了。這樣能更容易理解Ai的意義。

*如何解這個矩陣方程?這裡引入了矩陣奇異值分解(SVD)這一方法,能將目標矩陣以一定規則分解為三個矩陣連乘。
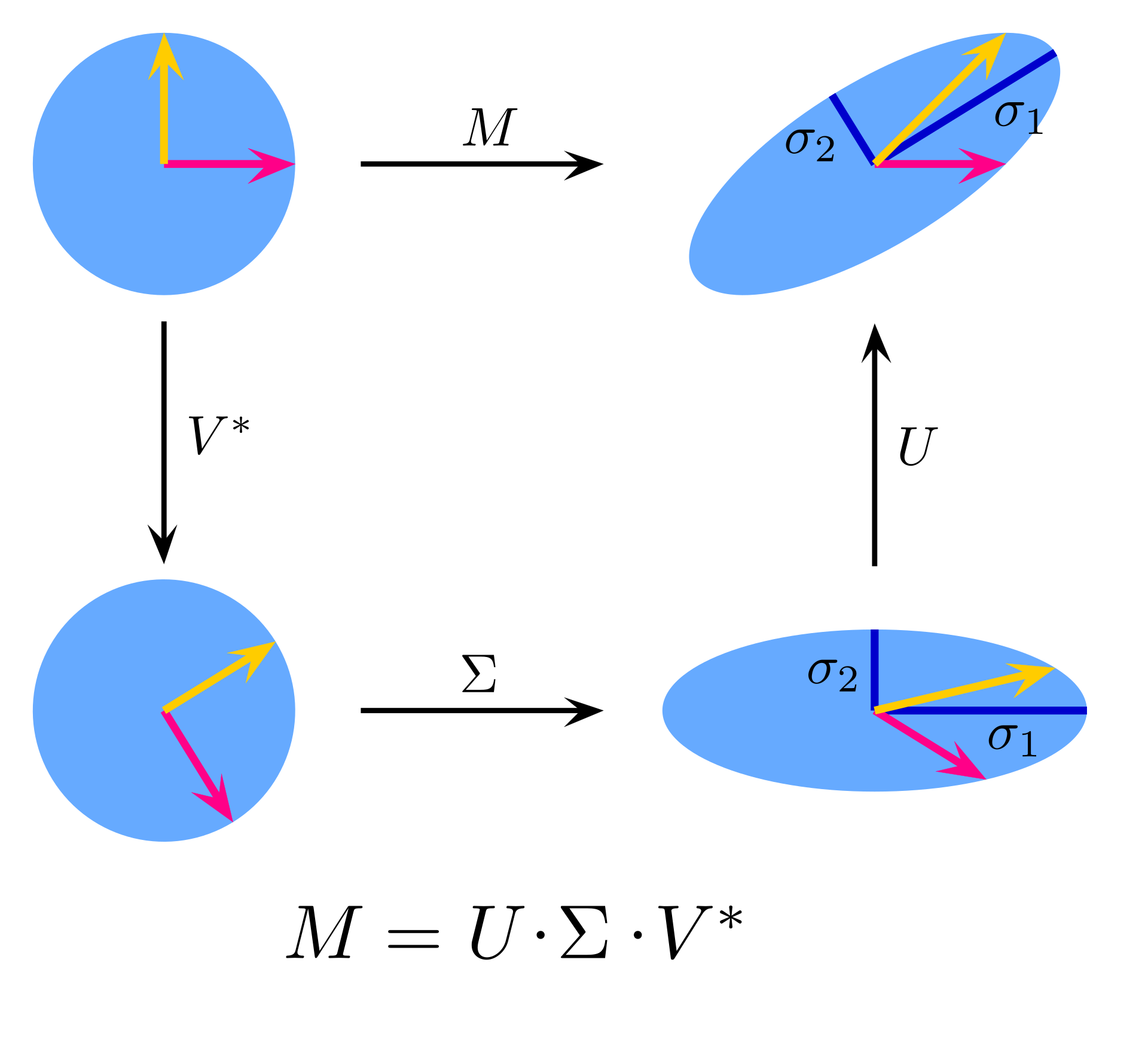
SVD圖示

*對於圖中公式的情況,SVD分解後的V的最後一列(V^T的最後一行)9個值就對應列向量h——並能直接得到矩陣H。

*圖中展示了SVD的兩種情況。對於原始矩陣的秩大於1的情況來說SVD的結果一定存在,且可能不唯一。
*其中U和V有著各自與轉置矩陣相乘都等於對應階的單位矩陣的特性。對於U是正交矩陣的情況可由如下計算步驟來推出一個解。
奇異值分解的計算步驟
- 計算矩陣A的轉置:首先,計算矩陣A的轉置矩陣A^T。
- 計算AA^T的特徵值和特徵向量:接著,計算矩陣A與其轉置矩陣A^T的乘積AA^T,然後求出其特徵值和特徵向量。
- 計算A^TA的特徵值和特徵向量:然後,計算A^TA的特徵值和特徵向量。
- 構造U和V矩陣:將AA^T的特徵向量歸一化後構成矩陣U,將A^TA的特徵向量歸一化後構成矩陣V。
- 構造Σ矩陣:將AA^T的特徵值的平方根按降序排列,構成對角矩陣Σ。
*介紹到特徵值和特徵向量這一步就不繼續展開了,可以自行搜索網上的資料。而關於DLT和SVD文末會給出多條參考資料。
*SVD本身也是一種降維壓縮方式,在圖像分析領域被廣泛使用。
三、主動式立體視覺系統——Active stereo vision system
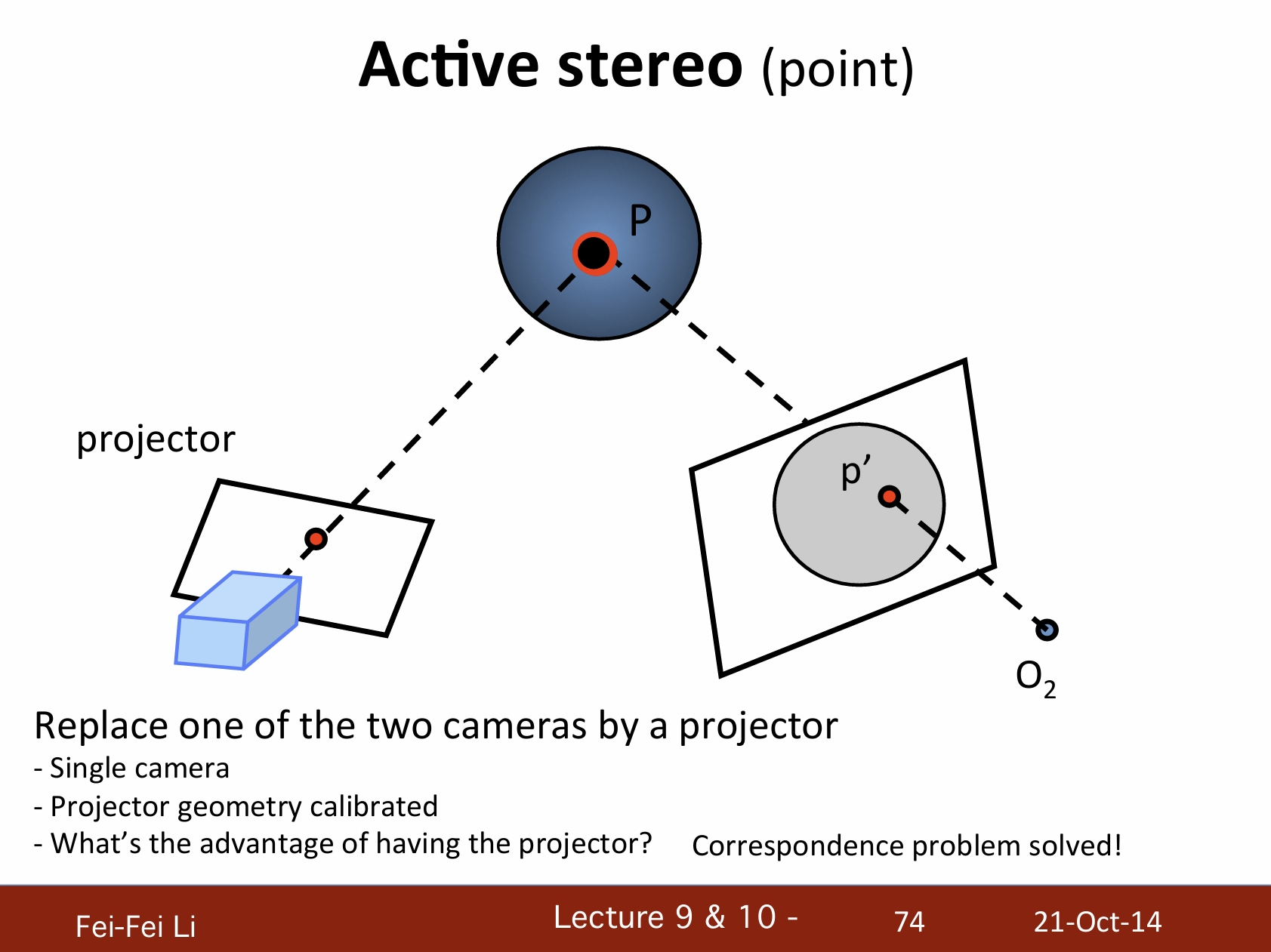
主動式立體視覺(點)
通過一個投影器(變換)來替換兩個攝像機中的一個:
- 單攝像機。
- 投影幾何已校準。
- 投影器的優勢是?解決了對應點問題。
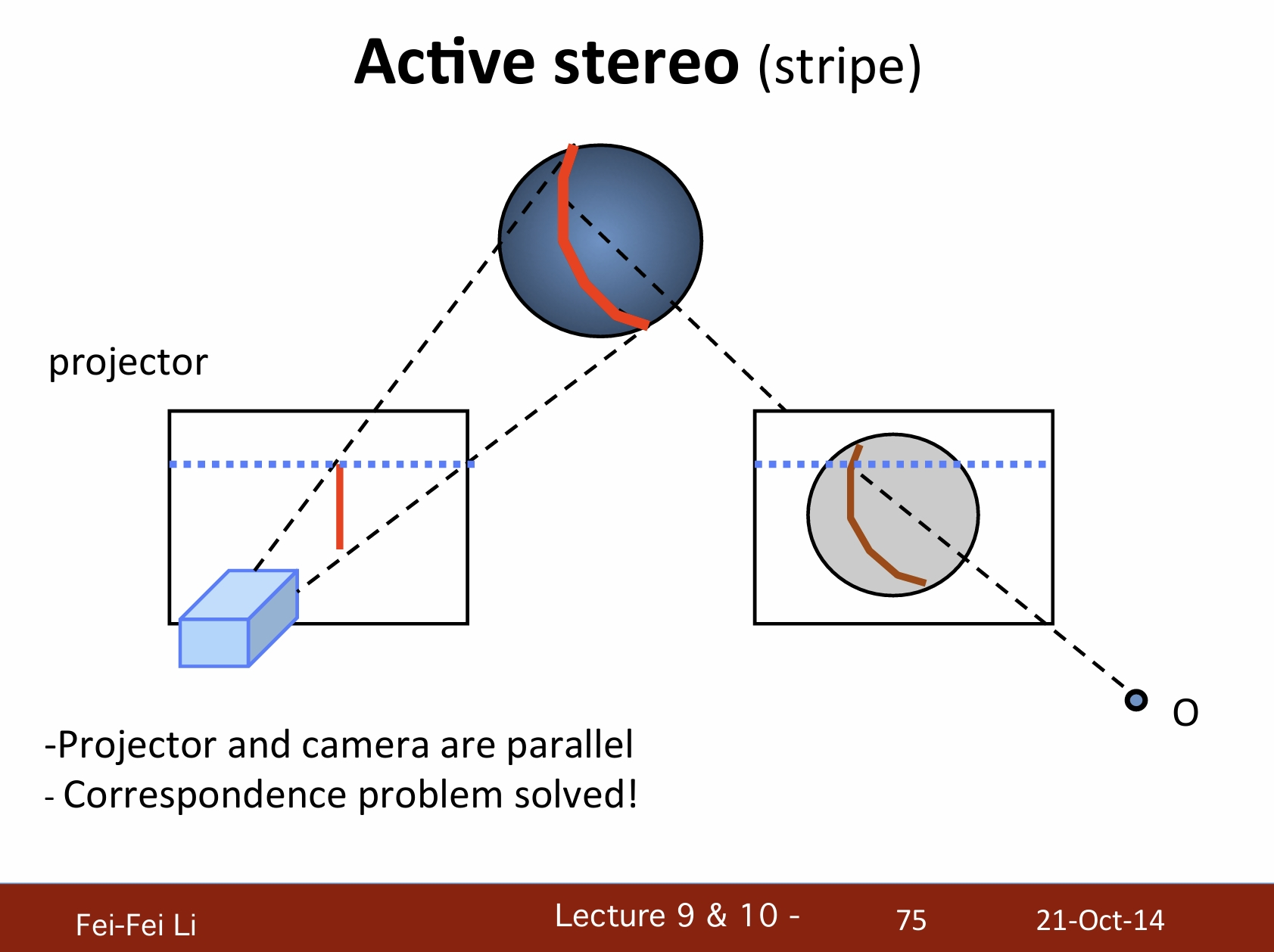
主動式立體視覺(條紋)
- 投影器和攝像機是平行的。
- 也解決了對應點問題。
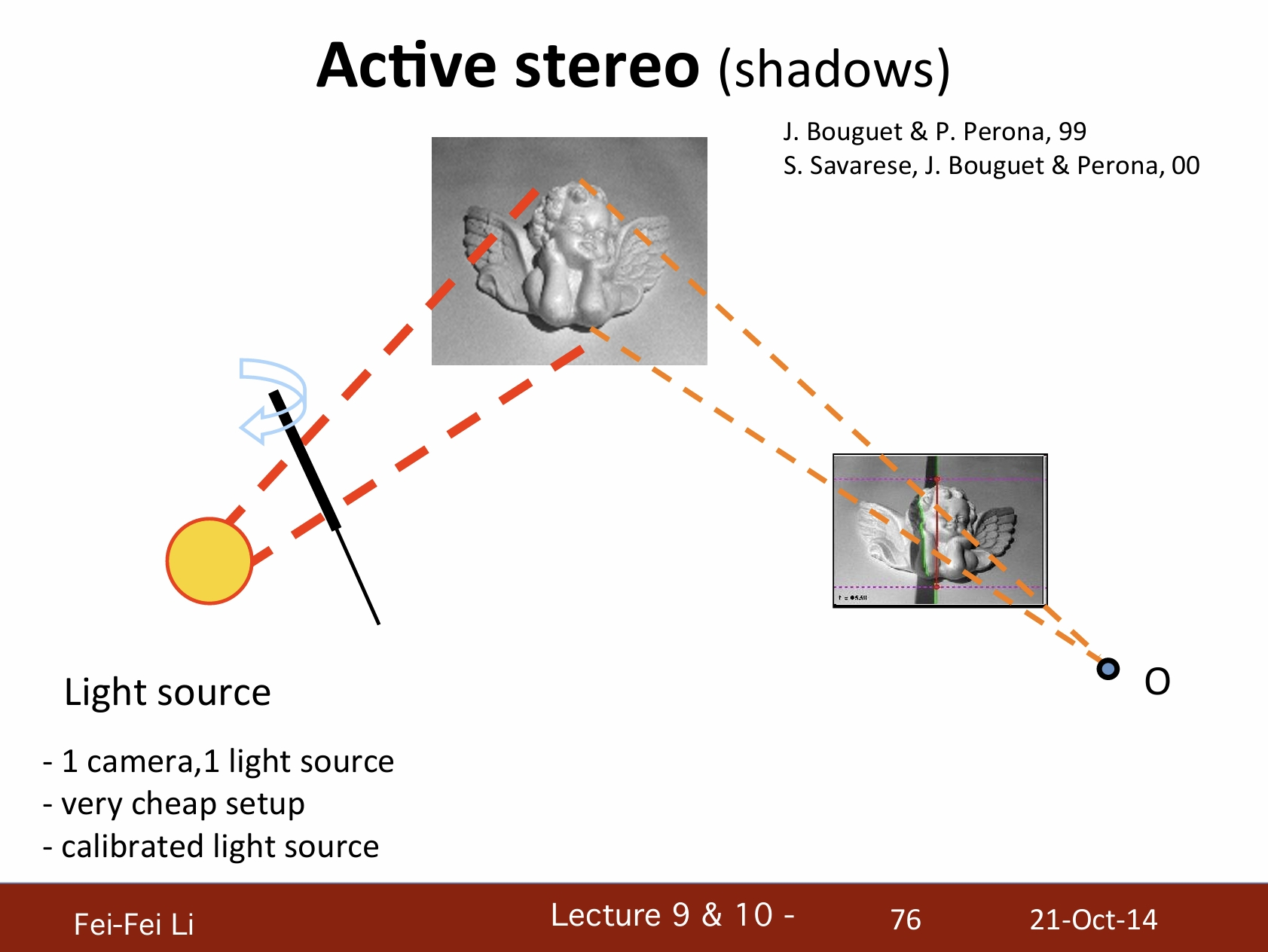
主動式立體視覺(陰影)
- 一個攝像機,一個光源。
- 非常易於設置。
- 已校準的光源。

*主動立體視覺——陰影的例子。
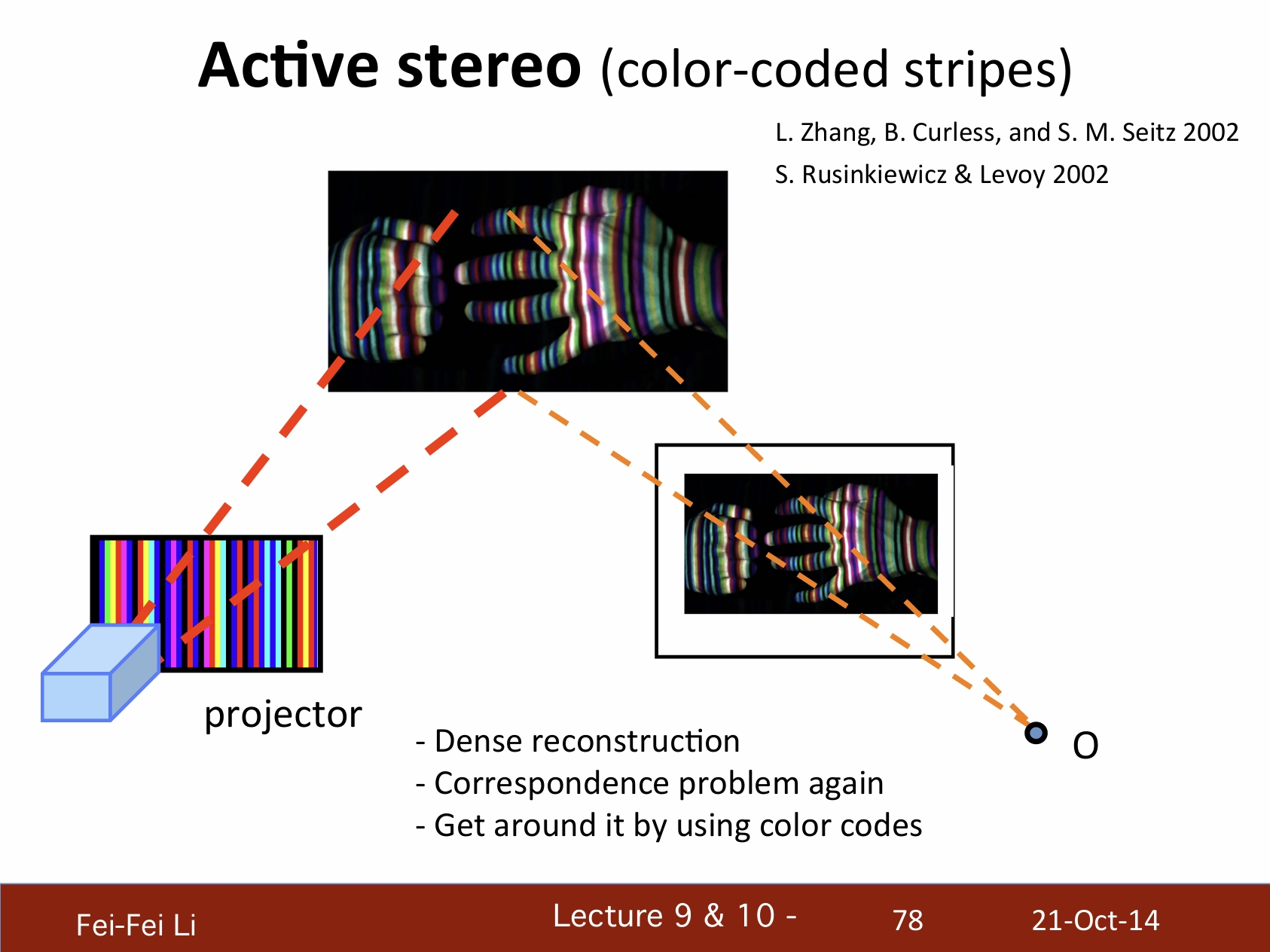
主動式立體視覺(顏色編碼的條紋)
- 密度重構
- 再次遇到對應點問題
- 通過顏色編碼來判明

快速形體獲取:投影器+立體攝像機。

主動式立體視覺(條紋)
*圖中展示的是斯坦福的“數字米開朗基羅”工程
光學三角測量:
- 每一道激光投影一根條紋
- 掃描整個物體的表面
- 這是結構光掃描的一個非常精確的版本
*這裡的激光是用來投影條紋並拍照的,核心方法還是基於圖像的立體視覺。後面略去了幾頁只有圖片的案例展示。
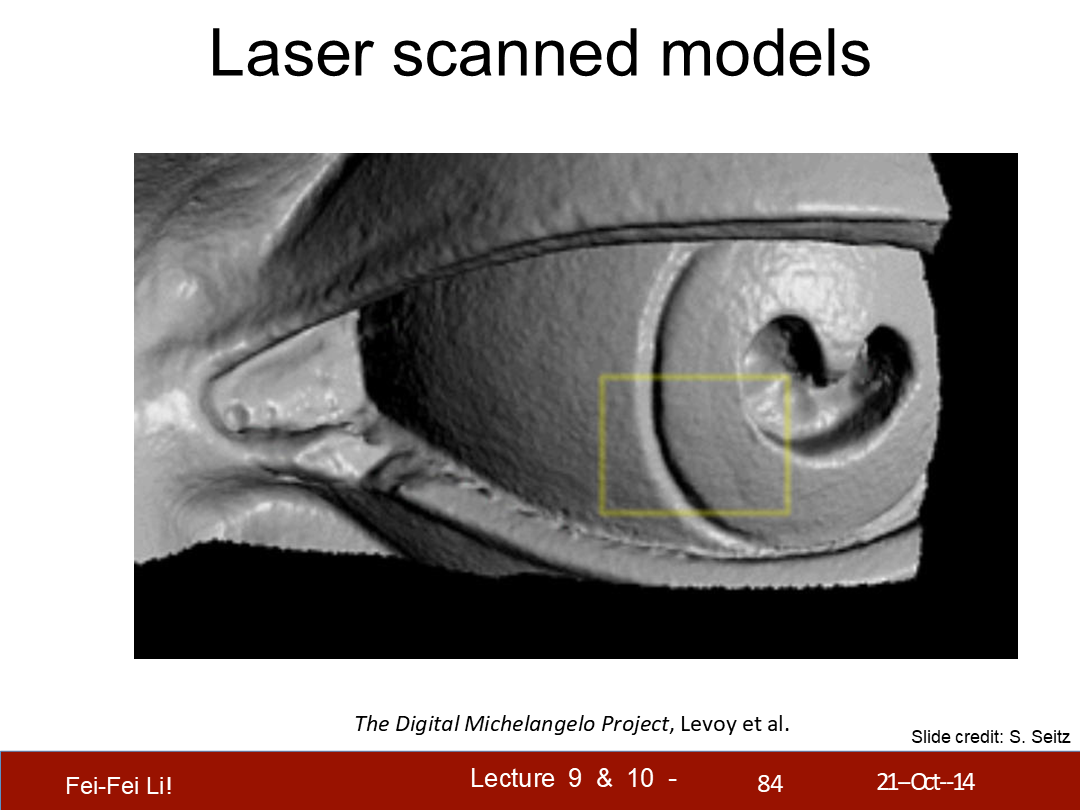
*圖中展示了眼部細節的一些情況。

*圖中展示了1毫米精度下的三角面數。
結語
啃完立體視覺的這篇課件後,在頭昏腦脹之餘也能深切的感受到這就是科技的發展——放在10多年前可能還是博士生以上才需要研究的領域,現在已經逐步成為了後來技術的基石。就好比圖形AI也不是憑空產生的,這篇課件裡介紹到的很多內容都構成了後來神經網絡中的基礎算法、輸入端或是數據處理層。
在B站Games系列課之下也有三維重建的專題,在一年時間內我肯定是會伴隨著把那個也看完。最終能達成“看懂圖形AI每一步在做什麼”是我的目標——對於超出能力看不懂的部分則保持敬畏之心。
雖然在上週的文章中誇了DeepSeek R1,但它的“幻覺程度很高”、“沒答案的時候亂編”的問題隨著大量的使用也比較明顯了。當然,讓一個AI不亂編的方法肯定有,關鍵是用AI的人不能迷信它的輸出。內容創作方面如果嘗試用它生成最終的文稿,很可能發生“生成5秒,查錯1小時”的情況——因為和事實交叉比對的還得是創作者自己。
在技術向的問題上,我個人的體驗是它幫助不大,因為本身網上技術交流的語料就少,正確的更少(很多實用向的引擎技術也沒有論文);而很多熱門話題的總結概括,則又容易被網上各種陰陽怪氣的語料汙染,生成讓人啼笑皆非的內容;比較好用的主要還是在“事實”、“常識”、“數據分析”等方面。
雖然現在的很多高科技已經足夠“魔法”了,提供給普通人的基本就是一個交互界面,但另一方面網上資料也很多——我還是想盡量打開黑盒看看。
下面是一些資料鏈接:
立體視覺的WIKI
上世紀關於自適應窗口尺寸立體匹配的論文(紙質掃描)
Fast Approximate Energy Minimization via Graph Cuts
一個基於SSD做圖像分析的Git案例
一篇Model-Based Stereo的介紹
一篇介紹DLT的Carnegie Mellon University的課件
介紹SVD的一篇很好的youtube講解
一篇SVD的比較詳細的知乎介紹