前言
在上一篇中我们进行了三维重构方面的简单介绍,并很快引入了第一步的主题——立体视觉。这次继续读斯坦福大学的这篇课件。
PPT部分以翻译为主,打星号的部分是我的个人理解或补充,主要是对课件中没解说的部分补充外部信息。
一、解决对应点问题——Solving the correspondence problem
*这部分课件中举例用的一些图都不算直观,有点难以看出左右两图的区别。
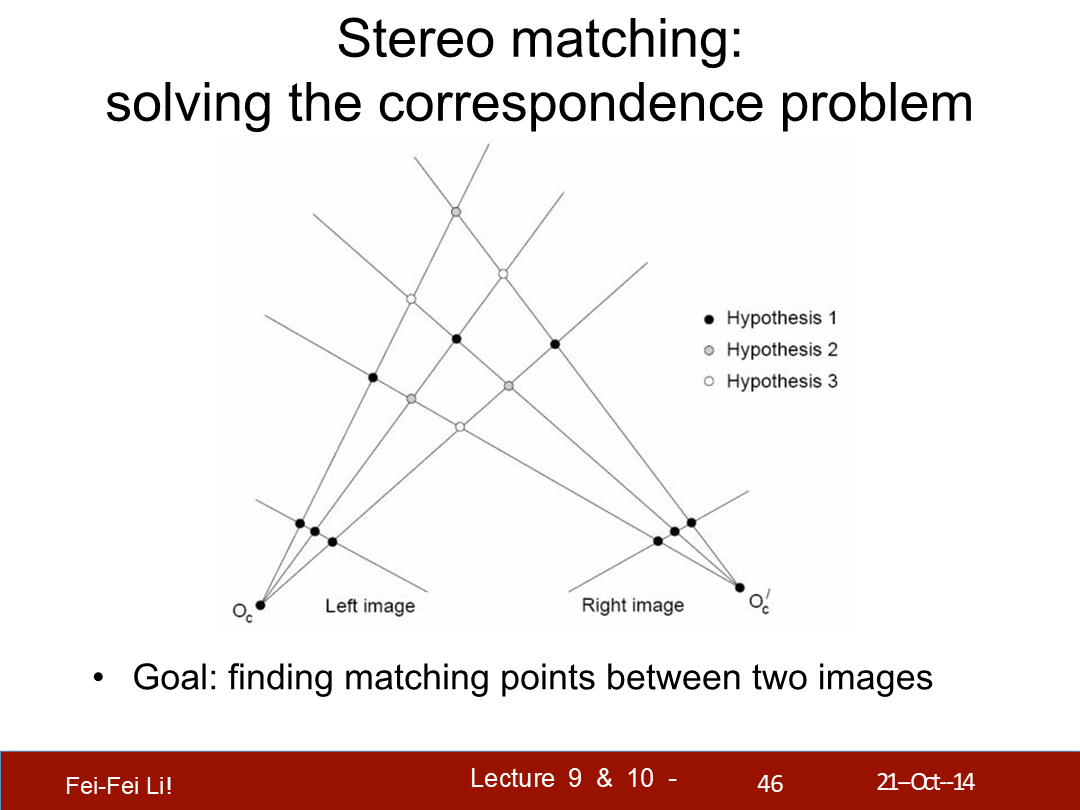
立体匹配:解决对应点问题
目标:找到两张图片中的对应点。(*Hypothesis,假设)

基础的立体匹配算法
对于第一张图中的每个像素:
- 找到右侧图中的对应极线
- 检测极线上的每个像素并选择最匹配的
- 三角测量匹配点以得到深度信息
最简单的情况——极线都是扫描线(与画面平行)。何时会发生这种情况?
*选择匹配点规则后面页会介绍到。另外,三角测量的方式在上一篇中介绍过了。

如果需要,可以将两张立体图片校正以变换极线为扫描线。(变成平行平面)
对于第一张图中的每个像素x:
- 找到右图中相对应的极线扫描线
- 检测极线上的每个像素并选择最匹配的x'
- 计算差异度x-x',将深度设为它的反比(如图)

对应点问题
让我们做一些假设来简化匹配问题:
- 基线相对很小(和场景中点的深度对比而言)
- 这样大部分场景中的点都能在两个视图中可见
- 并且,匹配的区域在外观上是相似的

通过相似性约束来查询对应点
沿着右侧的扫描线滑动一个(检测)窗口,并比较左侧中相关联窗口的结果。
匹配开销:SSD(后一页提到了,差方和)或归一化相关系数。
*两者都是统计学上量化数据的方式。
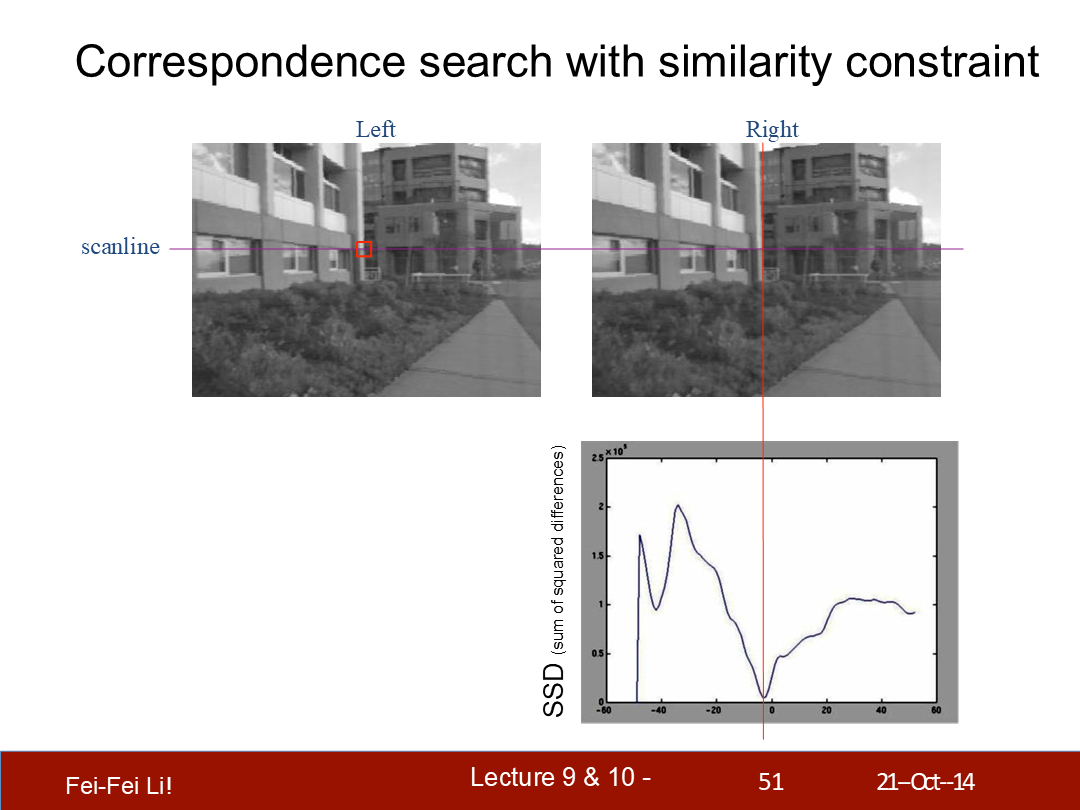
*这里横轴是差异度(disparity),纵轴是差方和(Sum of Squared Differences)。这里对比的是左侧的一个位置和右侧一条线上的窗口——可以看到图中的例子中最匹配的点肯定不是差异度为0的,而是接近0。

这里是一段伪代码示例,长宽对应一个检测窗口的尺寸
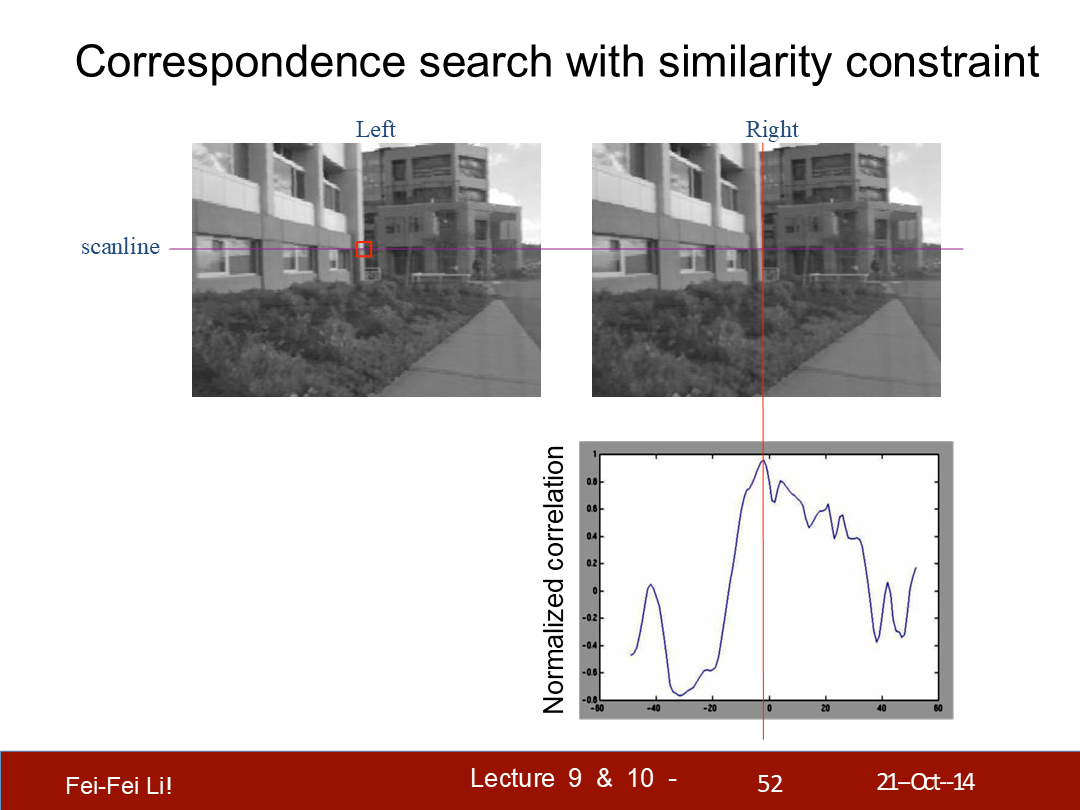
*这里纵轴换成了归一化相关系数。不管哪种计算方式,都是对比的窗口像素差异。
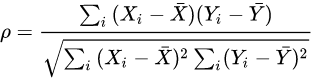
归一化相关系数的定义。可以看出相似度越高越接近1。

(不同)窗口尺寸的效果
- 小窗口:更多细节,更多噪声。
- 大窗口:更平滑的差异图,更少噪声。
*这里是差异图可视化之后的结果,而能表现为灰度图应该是使用的归一化相关系数作为颜色显示,并且处理完整张图像的结果。

相似性约束
- 两张图中对应的区域应该在外观上类似
- 而不对应的区域应该在外观上不同
- 那么何时这一相似性约束会失效?

相似性约束的局限
(图中顺序依次是):无纹理的表面、剔除或重复、高光表面。

窗口查找的结果
*图中左侧是基于窗口的匹配结果,右侧是事实结果(很多算法实验都会配Ground truth结果作比较)。颜色图展示的是基于还原深度信息的物体轮廓。

*这里指出了基于图切割算法能有更好的结果。其中涉及了用图论思想优化图像划分,后续这个脉络的算法都被称为min-cut/max-flow算法。
*之前基于窗口的算法是一种局部算法,而图切割算法是一种全局算法。
*图论的部分超出我个人能解释的能力范围了,文末会给出2001年这篇论文的链接。

基线的作用
- 小的基线:较大深度误差。
- 大的基线:产生难以查询的问题。
*图中反映了两种情况,通过蓝色和红色包围的区域表示。不过左侧的示意图并没有表现出小的基线相对大的基线能更确定点的位置,实际上两者的观察点距离应该是差距很大的。
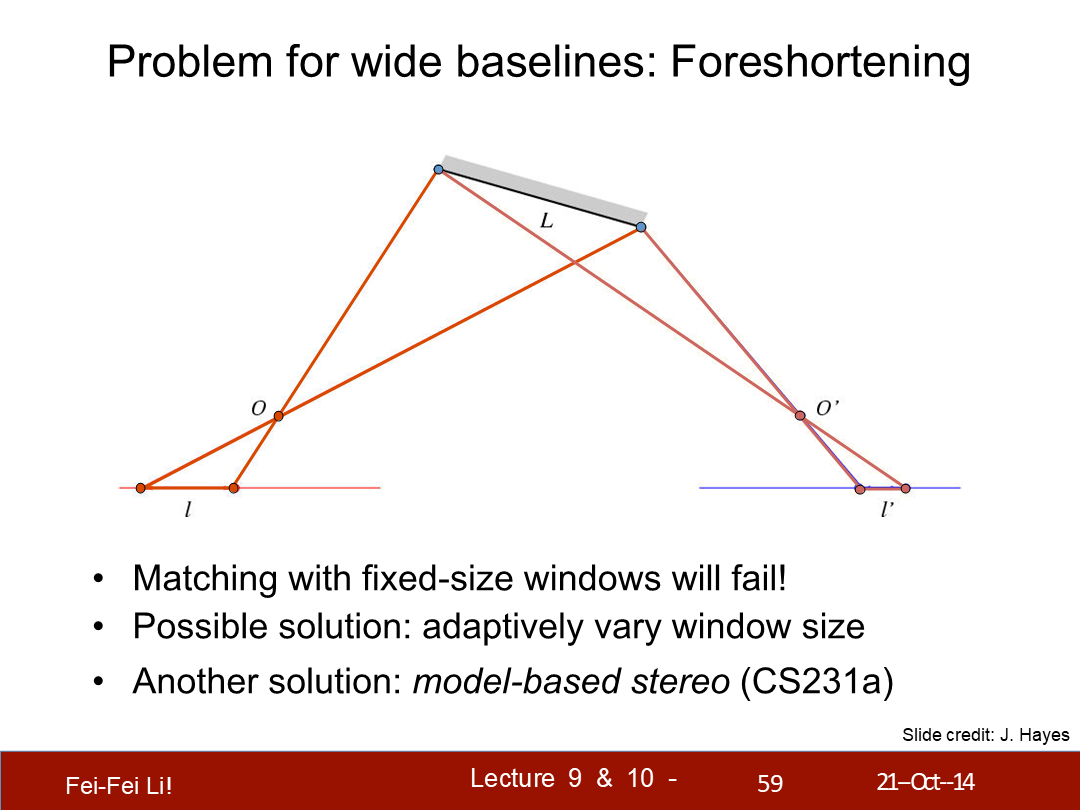
宽基线的问题(的解决):透视法缩绘
- (宽基线的情况)按固定尺寸的窗口匹配将失败。
- 可行的解决方案:自适应的窗口尺寸。
- 另一个解法:基于模型的立体查询。
*这里的model-based指先生成近似模型,再辅助计算点的相关性,这里摘录了1996年的一篇论文中提出的概念:
Model-based stereo differs from traditional stereo in that it measures how the actual scene deviates from the approximate model, rather than trying to measure the structure of the scene without any prior information. The model serves to place the images into a common frame of reference that makes the stereo correspondence possible even for images taken from relatively far apart.
译:Model-based的立体查询与传统立体查询的不同是,它通过与近似模型的偏差来度量(估算)实际场景,而不是尝试在没有任何前置信息的前提下来度量场景的结构。这一模型能提供特定帧(观察位置)的参照,使立体相关匹配变得可行——即使是从相当远的观察距离。
*这里的近似模型生成是从其它的一些参照方式(例如平面识别等)来构建,并辅助提高相关点匹配的准确性。虽然这篇课件主要介绍的是点与点之间的对应算法,但上一篇中介绍的各种方式(纹理、明暗等)都能辅助立体视觉的匹配过程。
二、单应变换——Homographic transformation

回顾:2D中的变换
*(只在平面上的)特定情况中,二维变换矩阵是2X2的,其中R代表旋转,t代表平移。
*它有着3的自由度(DOF,上篇中介绍过这个概念);能保持距离(区域);刚性物体间符合动量约束。

*普适的情况中,变换矩阵如图所示(a1-a9)。
*它有着8的自由度,保持共线性的特征。
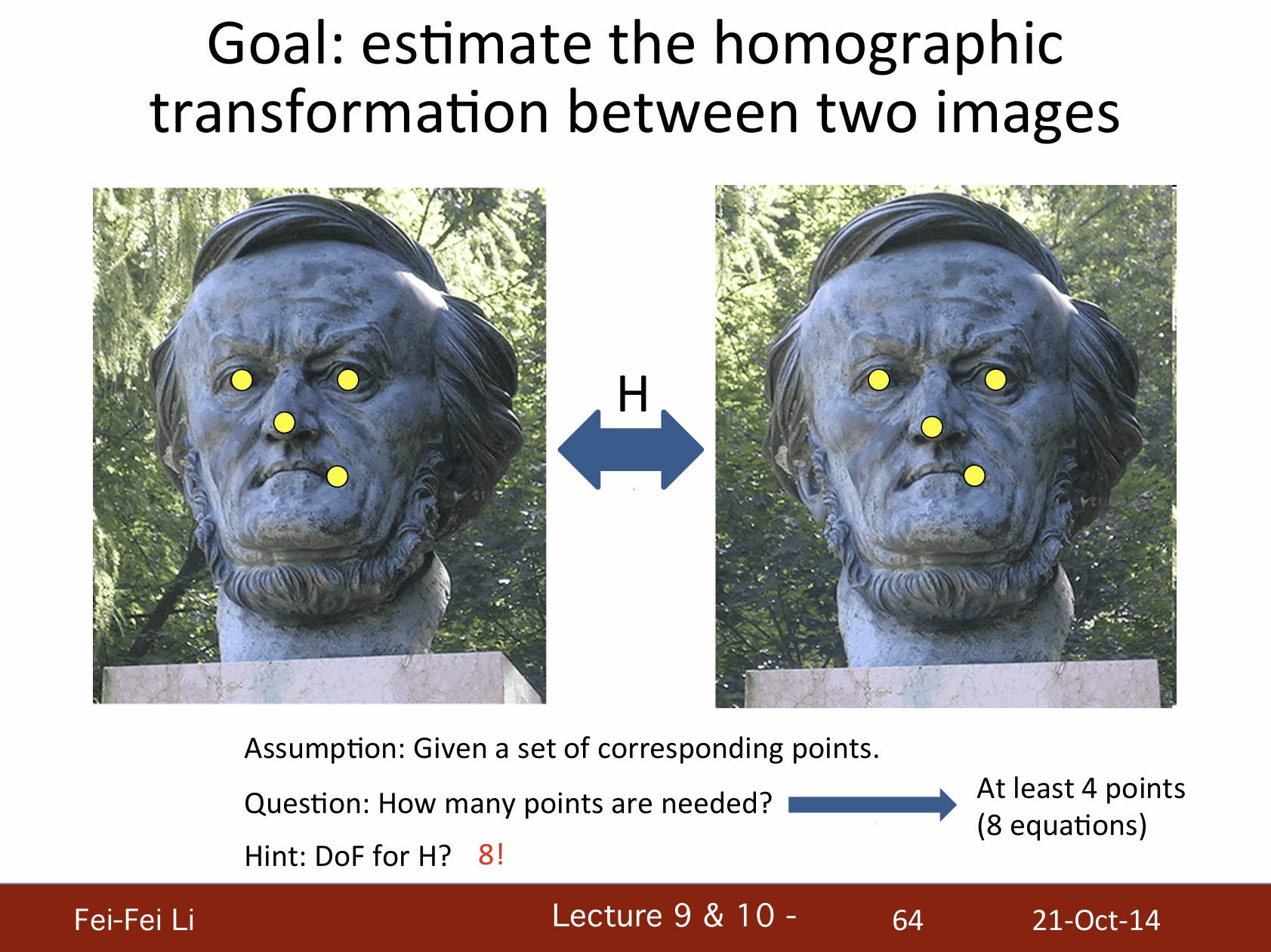
目标:估算两张图像之间的单应变换
- 假设:给定一组对应点。
- 问题:需要多少点?——至少需要4个点(8个方程)。
- 提示:变换矩阵H的自由度是8。

DLT算法(直接线性变换)
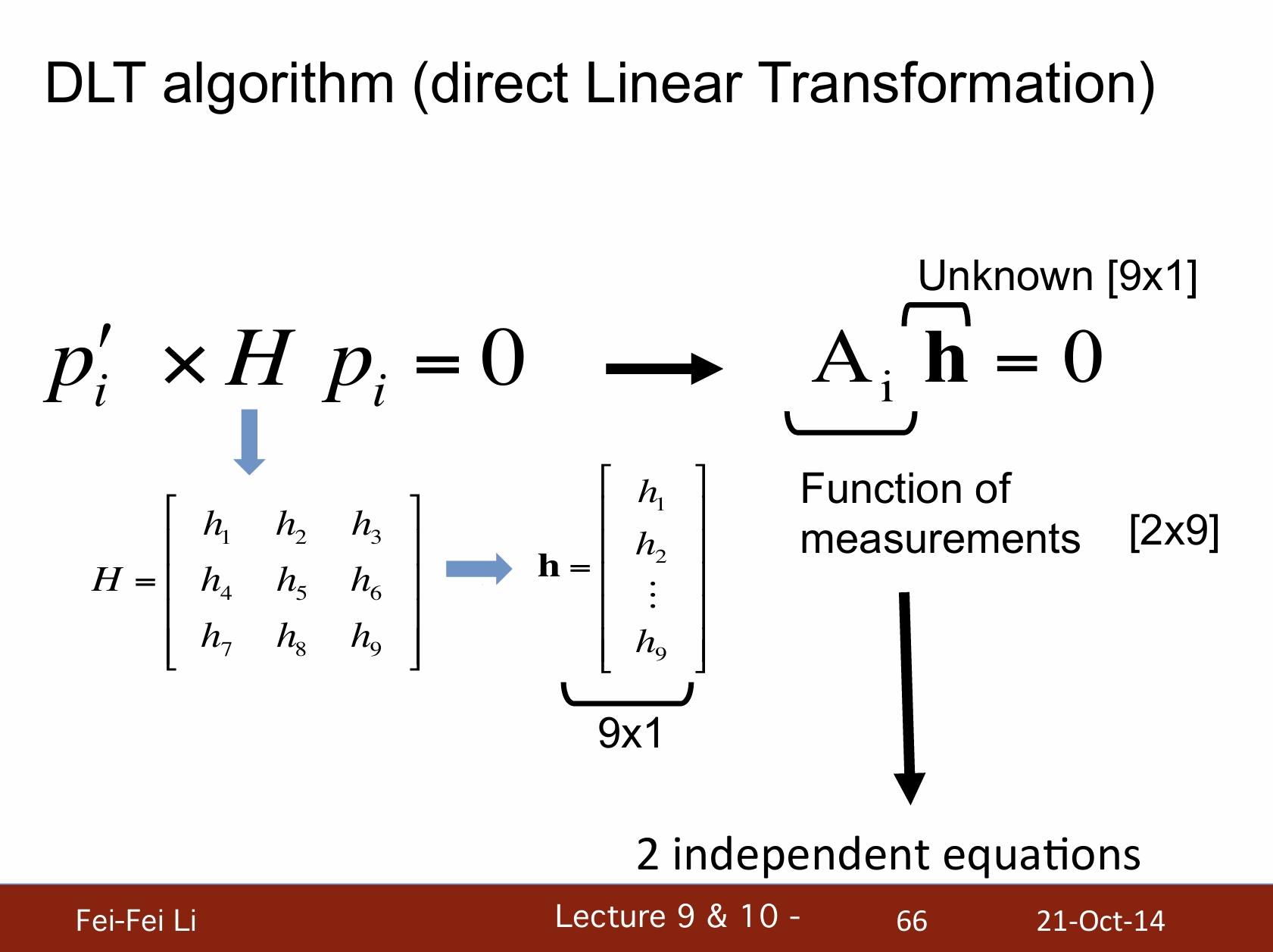
*DLT算法的目的是在已知对应点的情况下,通过建立线性方程组来求解摄像机的投影矩阵。
*这个课件的推导过程缺一点关键过程,下面通过资料介绍另一种推导方式:

*最上方的公式相当于pi'=H pi,展成三维坐标(向量)的形式。
*中间英文部分就不逐句翻译了,大致是在讲将矩阵乘开成方程组的形式,之后通过相除消去系数a的影响。
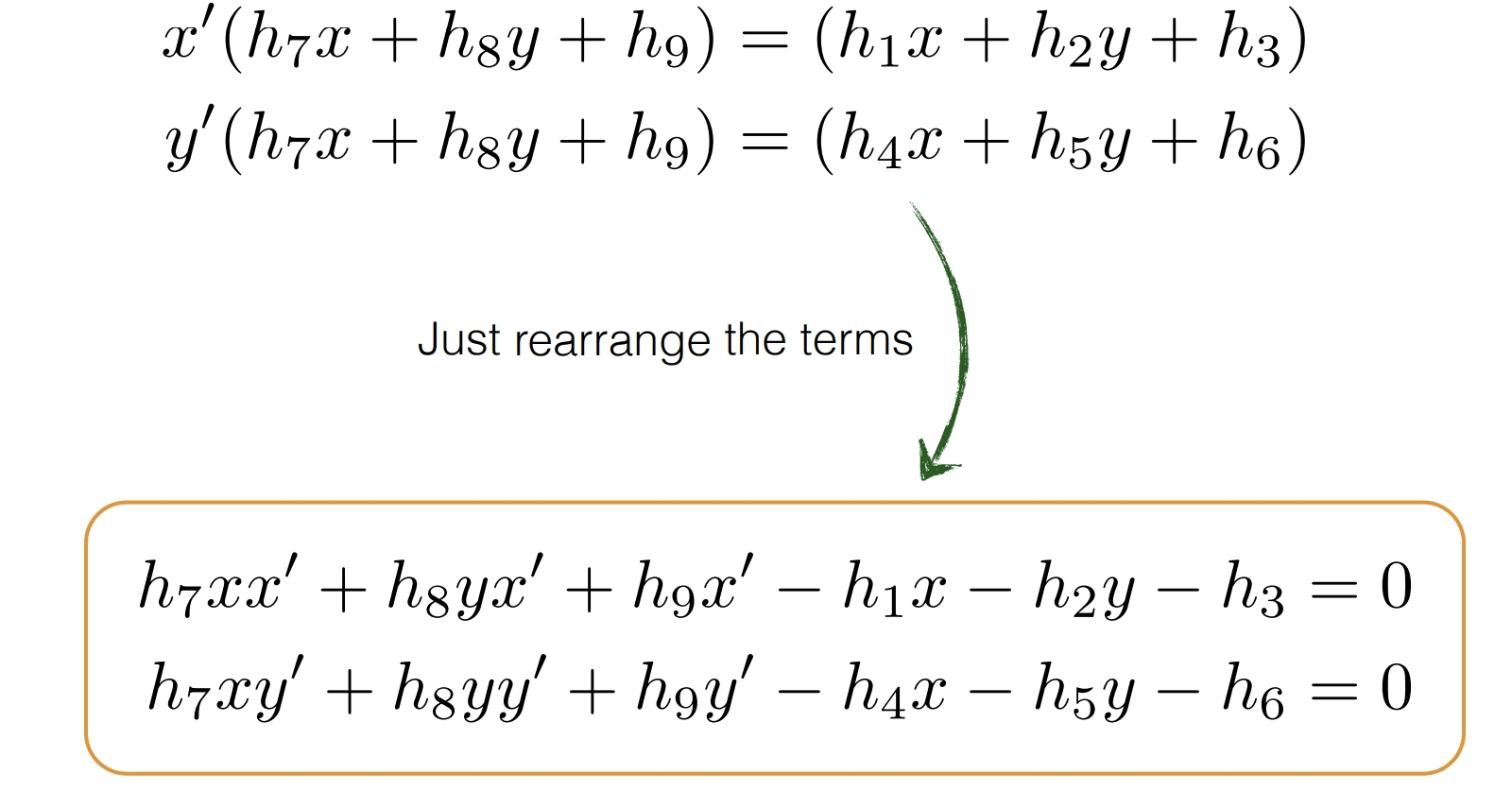
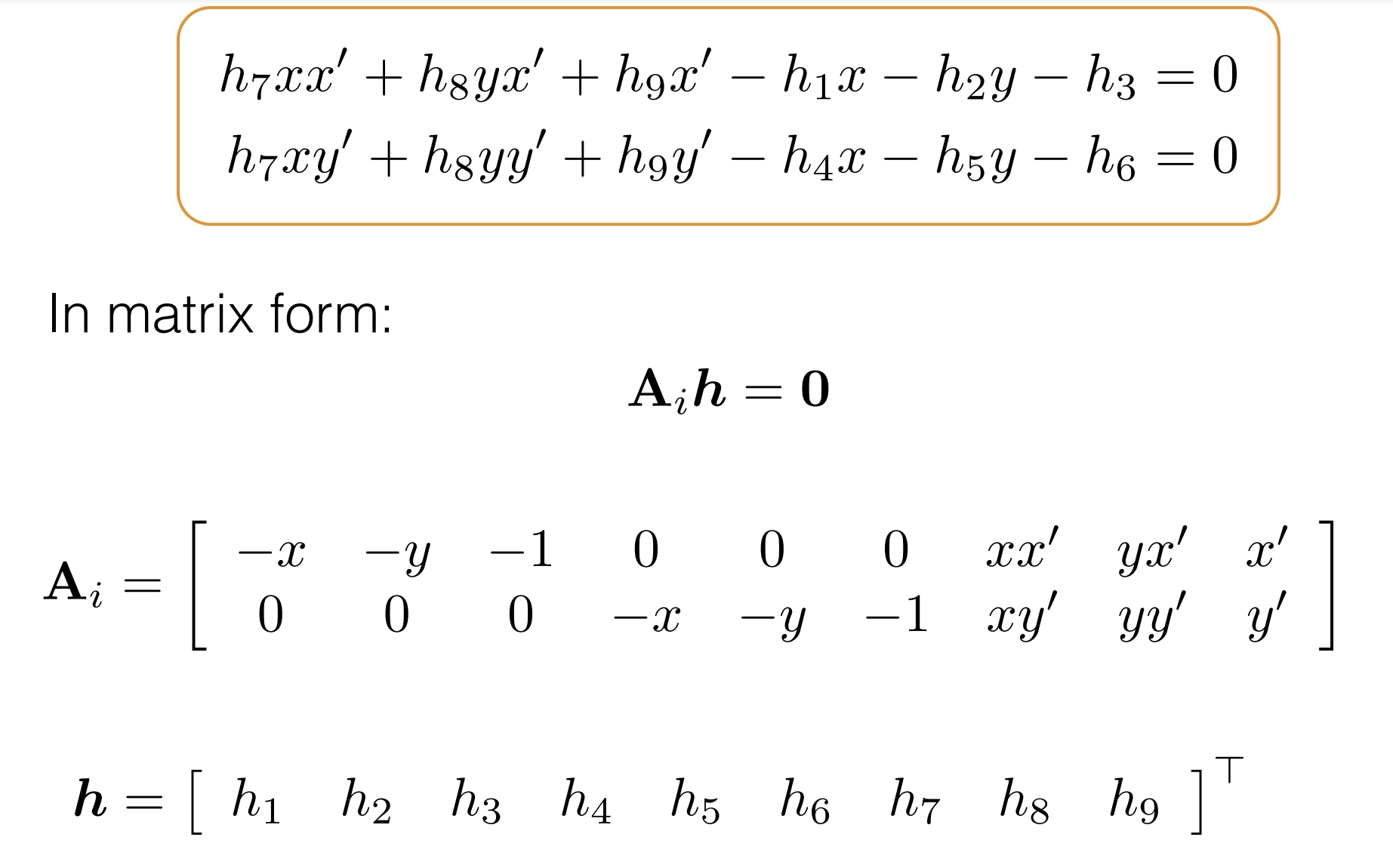
*将项重新排列并写成矩阵的形式,就和课件中一致了。这样能更容易理解Ai的意义。

*如何解这个矩阵方程?这里引入了矩阵奇异值分解(SVD)这一方法,能将目标矩阵以一定规则分解为三个矩阵连乘。
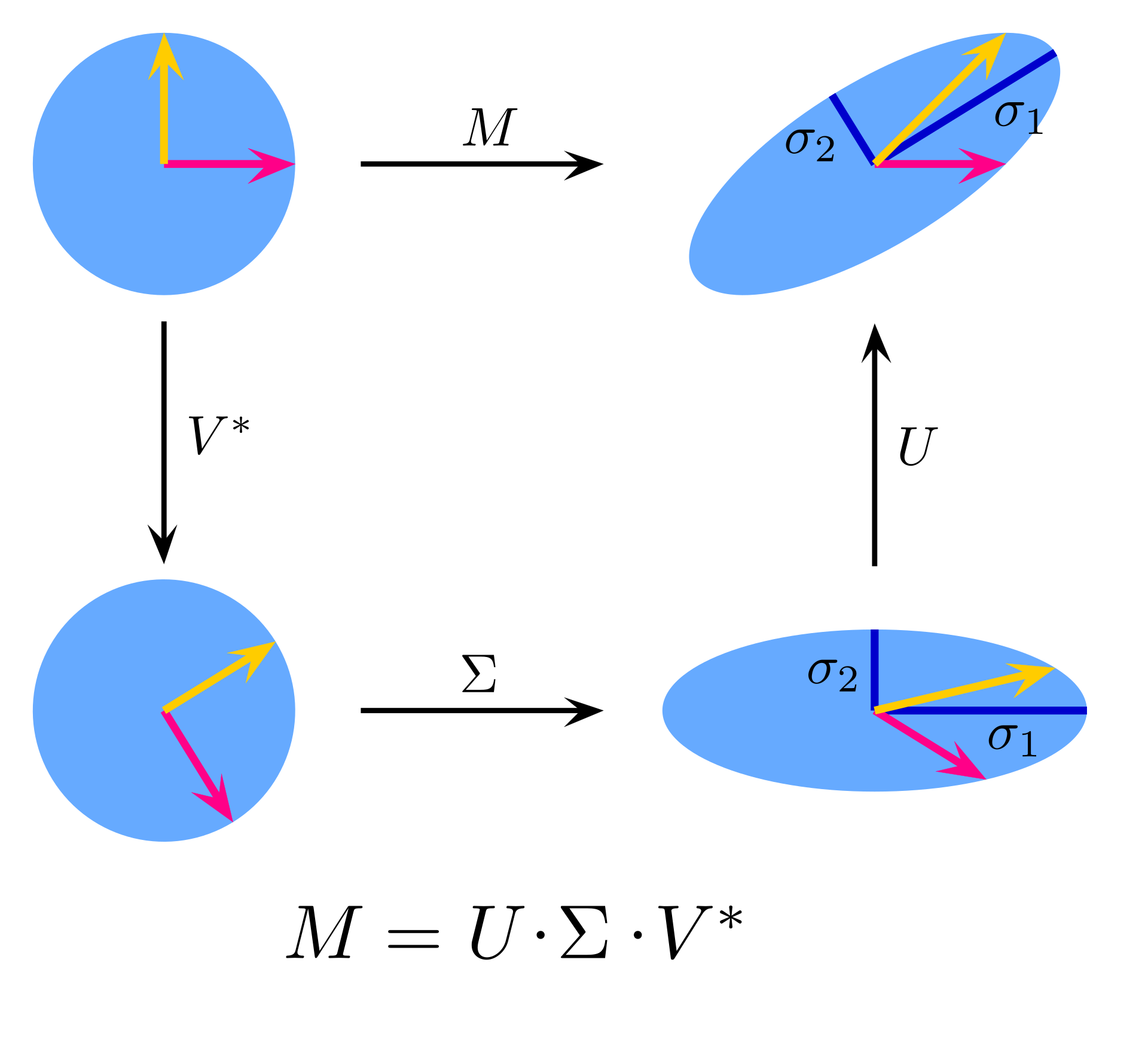
SVD图示

*对于图中公式的情况,SVD分解后的V的最后一列(V^T的最后一行)9个值就对应列向量h——并能直接得到矩阵H。

*图中展示了SVD的两种情况。对于原始矩阵的秩大于1的情况来说SVD的结果一定存在,且可能不唯一。
*其中U和V有着各自与转置矩阵相乘都等于对应阶的单位矩阵的特性。对于U是正交矩阵的情况可由如下计算步骤来推出一个解。
奇异值分解的计算步骤
- 计算矩阵A的转置:首先,计算矩阵A的转置矩阵A^T。
- 计算AA^T的特征值和特征向量:接着,计算矩阵A与其转置矩阵A^T的乘积AA^T,然后求出其特征值和特征向量。
- 计算A^TA的特征值和特征向量:然后,计算A^TA的特征值和特征向量。
- 构造U和V矩阵:将AA^T的特征向量归一化后构成矩阵U,将A^TA的特征向量归一化后构成矩阵V。
- 构造Σ矩阵:将AA^T的特征值的平方根按降序排列,构成对角矩阵Σ。
*介绍到特征值和特征向量这一步就不继续展开了,可以自行搜索网上的资料。而关于DLT和SVD文末会给出多条参考资料。
*SVD本身也是一种降维压缩方式,在图像分析领域被广泛使用。
三、主动式立体视觉系统——Active stereo vision system
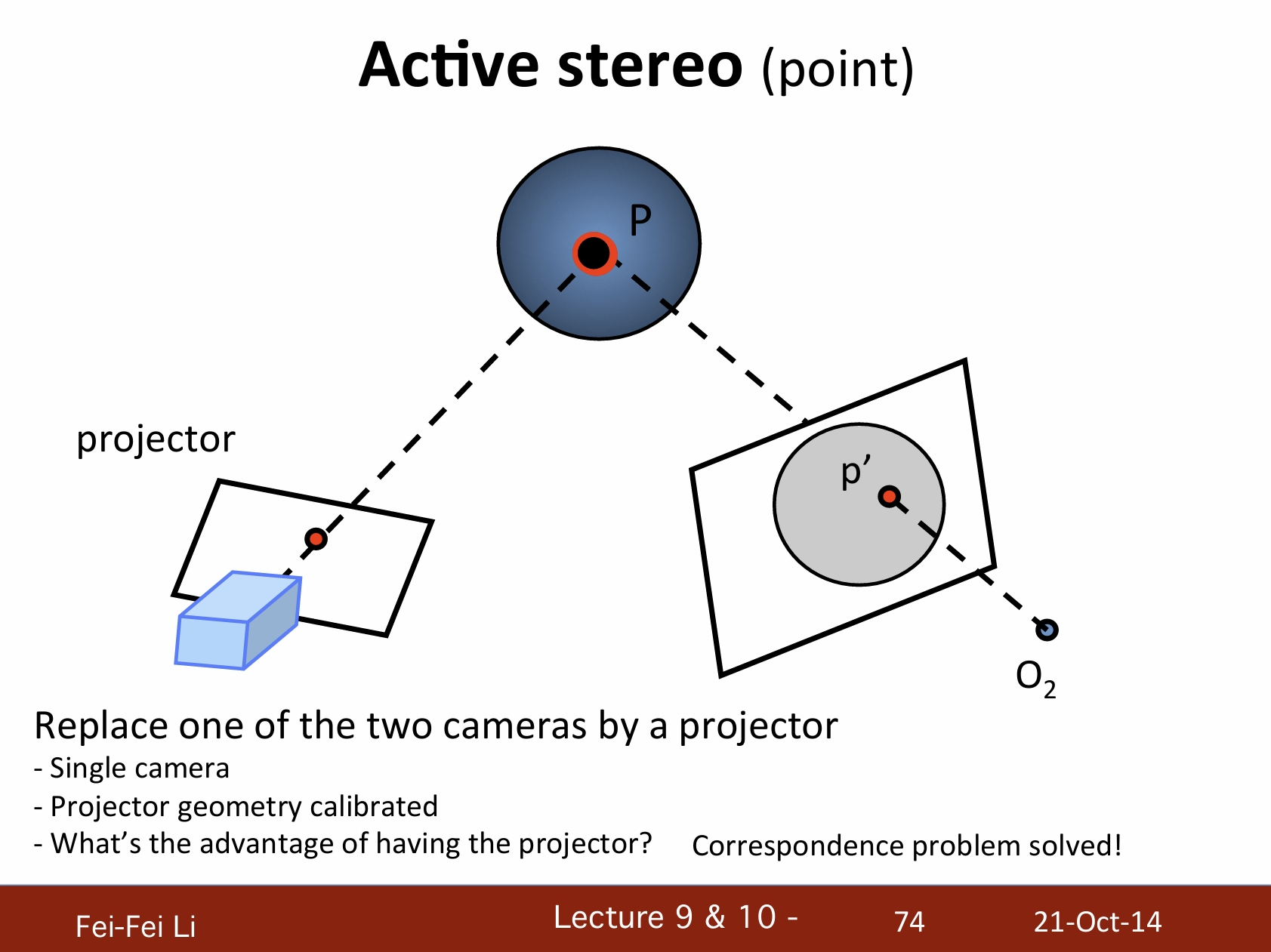
主动式立体视觉(点)
通过一个投影器(变换)来替换两个摄像机中的一个:
- 单摄像机。
- 投影几何已校准。
- 投影器的优势是?解决了对应点问题。
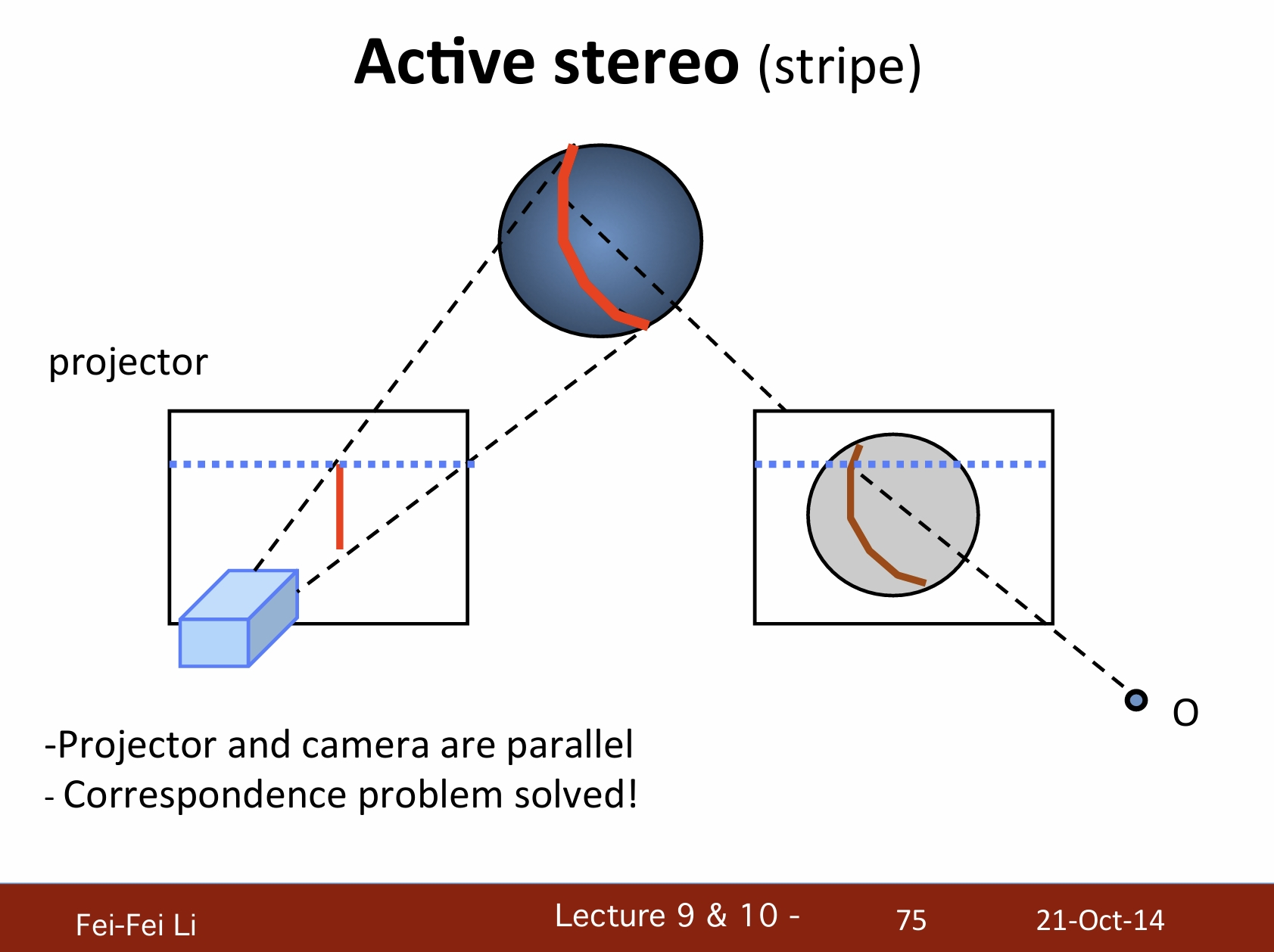
主动式立体视觉(条纹)
- 投影器和摄像机是平行的。
- 也解决了对应点问题。
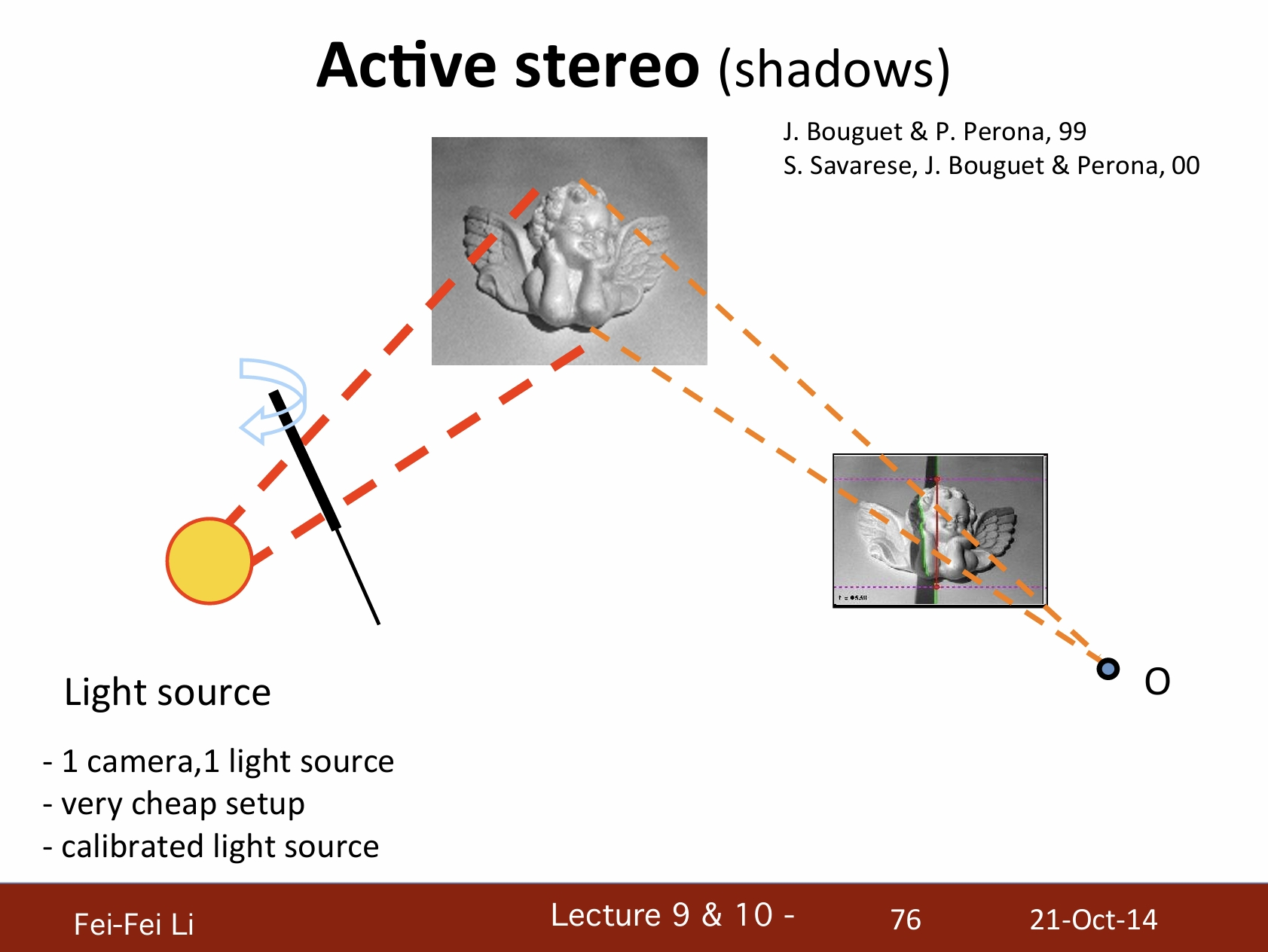
主动式立体视觉(阴影)
- 一个摄像机,一个光源。
- 非常易于设置。
- 已校准的光源。

*主动立体视觉——阴影的例子。
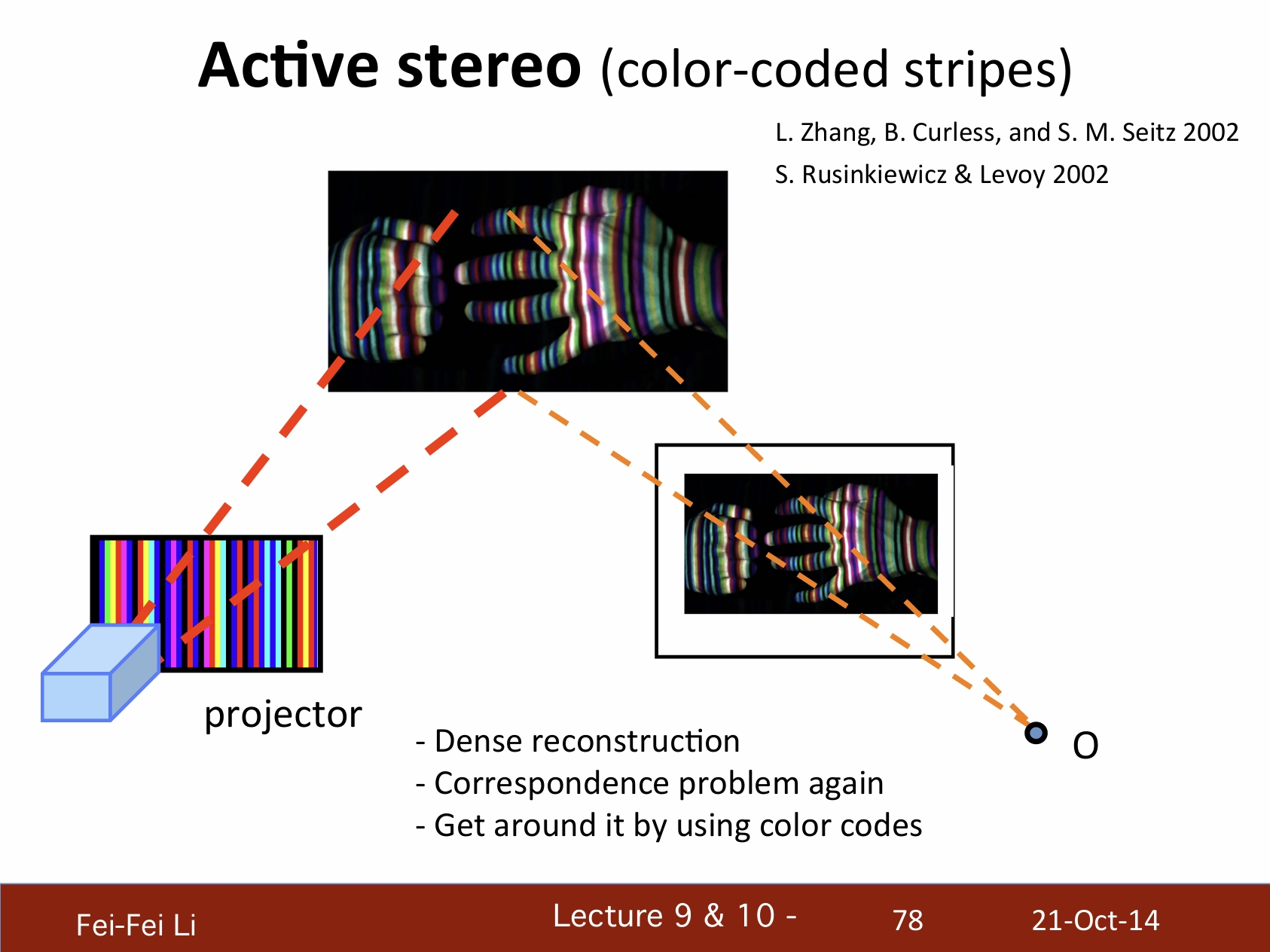
主动式立体视觉(颜色编码的条纹)
- 密度重构
- 再次遇到对应点问题
- 通过颜色编码来判明

快速形体获取:投影器+立体摄像机。

主动式立体视觉(条纹)
*图中展示的是斯坦福的“数字米开朗基罗”工程
光学三角测量:
- 每一道激光投影一根条纹
- 扫描整个物体的表面
- 这是结构光扫描的一个非常精确的版本
*这里的激光是用来投影条纹并拍照的,核心方法还是基于图像的立体视觉。后面略去了几页只有图片的案例展示。
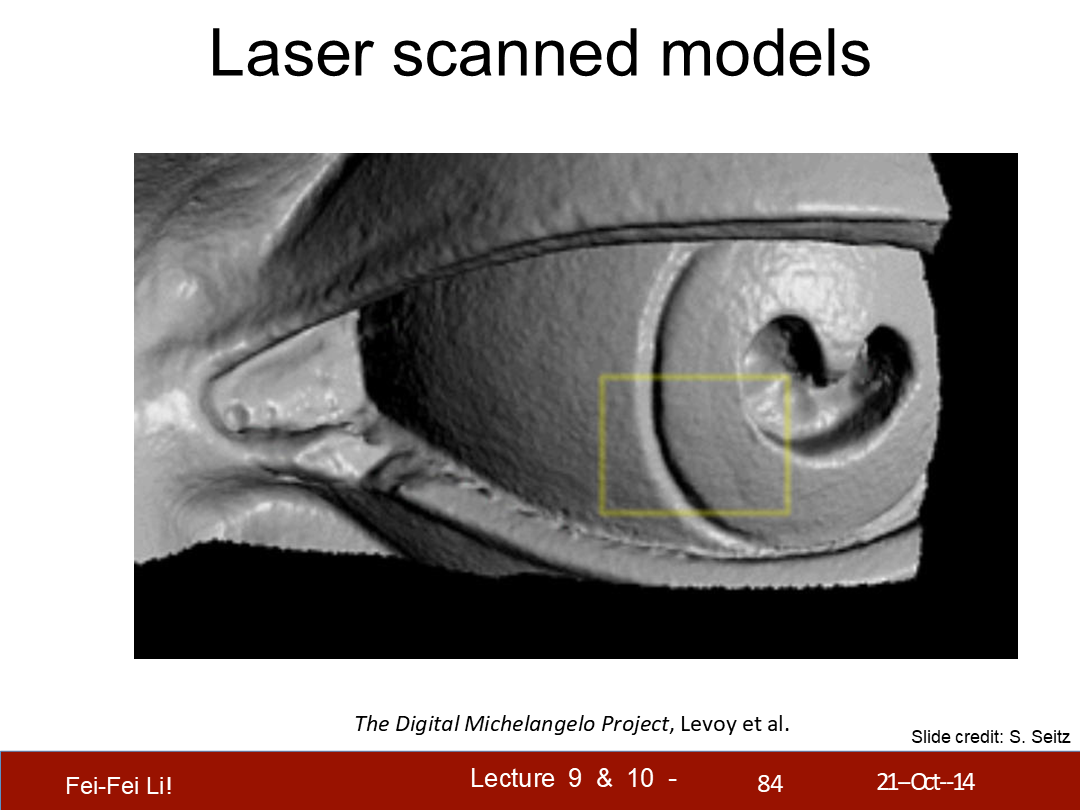
*图中展示了眼部细节的一些情况。

*图中展示了1毫米精度下的三角面数。
结语
啃完立体视觉的这篇课件后,在头昏脑胀之余也能深切的感受到这就是科技的发展——放在10多年前可能还是博士生以上才需要研究的领域,现在已经逐步成为了后来技术的基石。就好比图形AI也不是凭空产生的,这篇课件里介绍到的很多内容都构成了后来神经网络中的基础算法、输入端或是数据处理层。
在B站Games系列课之下也有三维重建的专题,在一年时间内我肯定是会伴随着把那个也看完。最终能达成“看懂图形AI每一步在做什么”是我的目标——对于超出能力看不懂的部分则保持敬畏之心。
虽然在上周的文章中夸了DeepSeek R1,但它的“幻觉程度很高”、“没答案的时候乱编”的问题随着大量的使用也比较明显了。当然,让一个AI不乱编的方法肯定有,关键是用AI的人不能迷信它的输出。内容创作方面如果尝试用它生成最终的文稿,很可能发生“生成5秒,查错1小时”的情况——因为和事实交叉比对的还得是创作者自己。
在技术向的问题上,我个人的体验是它帮助不大,因为本身网上技术交流的语料就少,正确的更少(很多实用向的引擎技术也没有论文);而很多热门话题的总结概括,则又容易被网上各种阴阳怪气的语料污染,生成让人啼笑皆非的内容;比较好用的主要还是在“事实”、“常识”、“数据分析”等方面。
虽然现在的很多高科技已经足够“魔法”了,提供给普通人的基本就是一个交互界面,但另一方面网上资料也很多——我还是想尽量打开黑盒看看。
下面是一些资料链接:
立体视觉的WIKI
上世纪关于自适应窗口尺寸立体匹配的论文(纸质扫描)
Fast Approximate Energy Minimization via Graph Cuts
一个基于SSD做图像分析的Git案例
一篇Model-Based Stereo的介绍
一篇介绍DLT的Carnegie Mellon University的课件
介绍SVD的一篇很好的youtube讲解
一篇SVD的比较详细的知乎介绍