前言
在高質量寫實渲染方面,UE引擎無疑是比Unity有著大幅領先的——這種領先主要在於渲染管線、全局光照、GPU集群渲染等方面,而我認為更重要的是在工具化實現高清渲染方面(即它是對於藝術家更友好的一款引擎)。最終這種開發和渲染特性傳達給玩家的感覺,就有例如“建模”更精細,整體光感更好更“真”,特效更亮更炫等。
但是反過來,大家可能也有一種感覺,就是現有的玩家硬件其實還不夠迎接這種技術升級。因為概括來說這種技術提供的是“不人工優化模型網格”的一種特權,它帶來的優勢更多是高清大型項目中的,對GPU有一定的算力要求,這從出發點上就一定程度上放棄了下沉到中低端設備的可能性。而且從文章中我們可以看出,其實不人工優化網格不等於不生成LOD,只是他們的LOD自動化構建有一套搭配他們新渲染方案的定製化的方案。
由於我不是從事UE方面開發的工作,因此雖然之前大概瞭解過UE5中實現巨量多邊形的大概思路,不過如果不過寫文章我可能不會進行逐頁翻譯粗讀。這次還是以讀分享文稿為主,由於篇幅原因就不摘錄講述者的原文了;打星號的部分還是我個人的一些補充說明。
另外,由於篇幅原因會分成兩次來讀,這篇文章是上篇。
1 目標

夢想——目標
- 像實現虛擬紋理一樣實現虛擬化幾何體(指像虛擬紋理突破尺寸和顯存限制)
- 不再有性能預算——多邊形數量、渲染調用次數、內存
- 直接使用電影質量的美術資源(不需要手動優化)
- 不損失質量
*看過當年UE5首次演示的應該有印象,這些就是它們的核心突破方向和宣傳點。

實際情況
——比虛擬紋理難得多
- 不僅是內存管理(地址映射)問題
- 幾何體的細節會直接產生渲染開銷
- 幾何體不具備一般可過濾的特性(不像紋理格式,可以應用各種信號學意義上的濾波方法)
2 備選方案分析與拆解
*這部分可以說探索了現代引擎渲染技術的方方面面,雖然長但是很有價值。
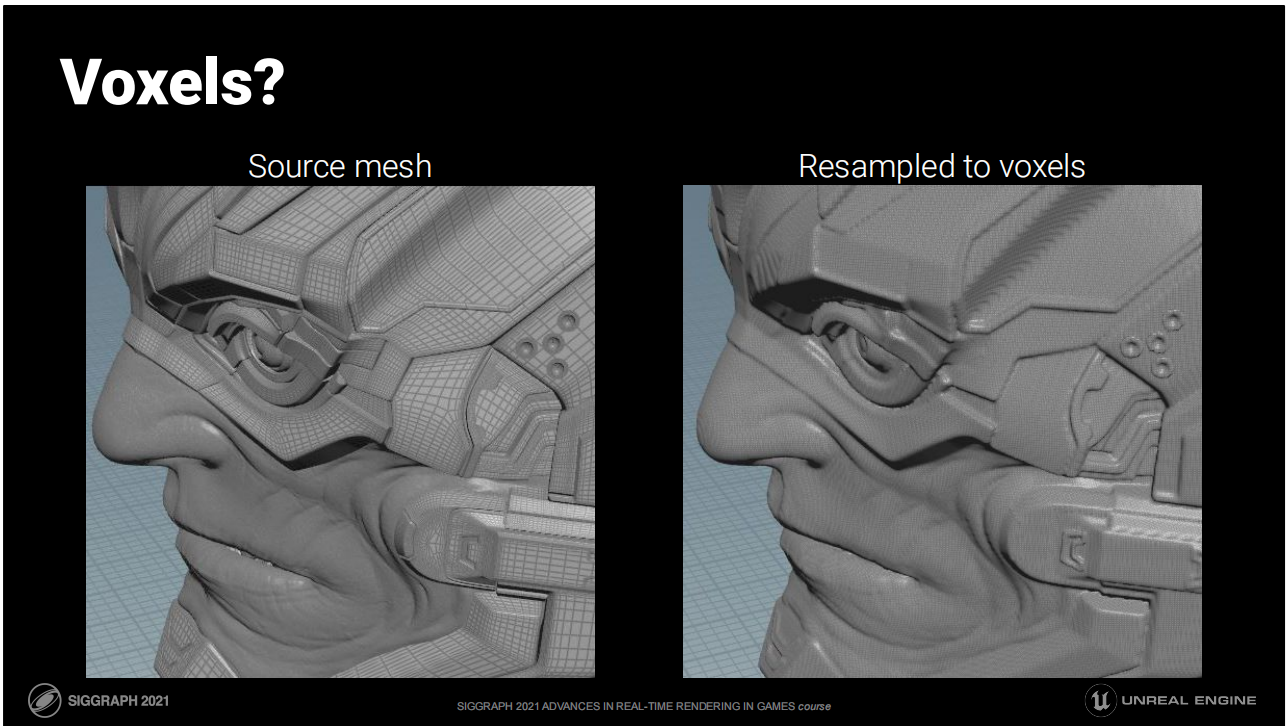
體素?
- 體素和隱式表面(通過函數定義的)通常是這類問題的有潛在優勢的討論方向。
- 圖中的原網格被重採樣成了右側的基於有向距離函數的體素(13M narrow band SDF voxels)。
- 體素方案的核心問題是採樣精度不好把握以及數據量相對較大(在相對無損的情況下)

——(網格體素化)並不是要完全改變全部CG工作流
- 支持把任何地方製作的網格體進行導入
- 仍有UV和細節紋理
- 只替代了網格,而不是紋理、材質和相關工具
——但儘管如此也帶來了更多難解的問題
- 體素如何與UV進行映射?
- 小於體素採樣精度的尺度下,無法表現細節和動畫
*基於這些現狀,體素目前無法稱為既有網格結構的替代方案。

細分表面?
- 細分表面既可以作為平滑增加細節的方案,也可以作為合併減面的方案。
- 採用自動化的網格細分並不會減少網格方面的限制,並且往往會為藝術家引入一些額外的限制,否則往往表現不如傳統的手工低面數網格模型。

替代(移位)紋理?
- 在某些情況下可以用低網格模型結合雕刻出的替代紋理數據,以類似法線貼圖的方式來提高精度
- 但對於右側的鐵鏈,是無法通過替代紋理來取一個低網格模型然後提高精度的,因為位移操作不能改變物體的“屬”(Genus 拓撲結構的概念,可以簡單理解成洞的數量)——就好比無法通過位移操作把圓球變成圓環
- 因此它不能作為一個常規普適的網格簡化方案

基於點的渲染?
- 單個點本身渲染會很快,但整體結果會有overdraw問題,或者需要補洞
- 點之間的幾何關係也沒有保存下來

最終選擇了三角形作為基礎渲染單元
儘管其它的一些方案也能圍繞其藝術風格上的特點構建一套完整的渲染系統,但Unreal需要普適的渲染方案。因此基於之前的一些對照方案,Nanite(UE引擎的一個模塊)選擇了三角形作為基礎渲染單元。
3 管線概述

GPU驅動的管線
——渲染器的現行模式
- 跨幀進行GPU場景數據保持
- 在場景物體變化時進行稀疏的更新
- 所有頂點和索引數據保存在一個大資源文件中
——每個渲染視圖中
- GPU實例剔除
- 三角形光柵化
——如果只繪製深度,整個場景可以在一個DrawIndirect(集成好的間接繪製指令)中完成
*強調是GPU驅動的意義在於減少與CPU的交互並儘量通過顯存內部處理、傳遞和運算數據,這也是現代渲染管線的趨勢。Cluster這個處理邏輯也是建立在GPU的並行計算優勢之上的。

三角集群剔除
- 將三角面分組為集群——為每個集群構建包圍盒數據
- 基於包圍盒剔除集群——視錐體剔除、遮擋剔除

遮擋剔除
- 遮擋剔除主要針對多層深度緩衝來進行(後續縮寫為HZB)
- 剔除計算時,依據包圍盒對應的屏幕空間尺寸來判斷合適的HZB層級
- 當屏幕尺寸小於等於4X4時,直接和最低層級的mip比較
*我之前一篇介紹遮擋剔除的文章裡詳細介紹過Hiz剔除是怎麼計算的。

遮擋剔除
- HZB怎麼來的?在還沒有渲染任何東西時是沒有HZB的(尤其是第一幀時)
- 把前一幀的Z-Buffer投射到當前幀呢?往往需要額外的補洞方案,且剔除的結果總是粗略和不夠保守的

雙pass遮擋剔除
- 上一幀可見的物體很大程度上會是在這一幀可見的,至少是一個視為遮擋物的好的選擇
- 雙pass的方案:繪製前一幀可見的物體;構建HZB;繪製上一幀不可見但這一幀可見的物體
- 這幾乎是一個完美的遮擋剔除方案:它是保守的(不會額外剔除),只在一些極端的可見性變化的情況會失效

從材質上解耦可見性屬性
By that I mean determining visibility per pixel (which is what depth buffered rasterization does) is disconnected from the material evaluation.
(這種解耦)意味這逐像素確定可見性——就像深度緩衝光柵化中做的一樣,將其和材質公式的關聯性去掉。
消除:
- 光柵化過程中的shader切換(which is 有性能開銷的)
- 材質評估過程中的重疊繪製
- 為避免重疊繪製而進行的前置深度pass
- 處理密集網格體時的像素多邊形低效
備選項:
- REYES(Render Everything Your Eye Sees,渲染所見的一切)
- 紋理空間
- 延遲渲染可用的材質
*這部分思路以及後面圍繞這個逐像素的策略進行的改裝就是UE5管線的精華了。

可見性緩衝
把幾何體信息寫入屏幕——深度、實例ID、三角形ID
逐像素的材質shader:
- 加載VisBuffer(可見性)
- 加載實例的空間變換數據
- 加載3個頂點的索引
- 加載3個頂點的座標
- 把座標變換到屏幕空間
- 得到目標像素的重心座標
- 加載和插值參數

可見性緩衝
聽起來不太現實?但實際不像它看起來那麼慢
- 有很多可用的緩存數據
- 沒有重疊繪製或像素多邊形低效問題
材質pass寫入了GBuffer——可以與我們其它的延遲著色渲染模塊集成
現在我們可以在1次繪製中渲染所有不透明幾何體
- 完全GPU驅動
- 不僅是深度的prepass(也是幾何體的繪製pass)
- 每個視圖僅光柵化三角形一次
*這部分可以說就是這個方案的核心,一些方面消耗雖然變高了,但另一些方面節省了。

次線性縮放
Linear scaling in triangles is not ok. We can’t achieve our goals of “just works no matter how much you throw at it” if we scale linearly
三角形的線性縮放是不OK的,如果不管引入多少三角形我們都僅線性縮放,我們就無法達成目標。(這裡scale直接理解成規模變化也沒問題)
Virtualized geometry is partly about memory. But ray tracing isn’t fast enough for our target even if it fit in memory
虛擬幾何體是部分關於(節省)內存的,但(對現有數據結構的)光線追蹤即使在內存達標的狀態下還是不夠快。

次線性縮放
In terms of clusters, we want to draw the same number of clusters every frame regardless of how many objects or how dense they are.
在集群方面,我們希望繪製相同的集群數量(和像素數量相關),無論每一幀有多少物體或密度如何。
It’s impractical to be perfect there but in general the cost of rendering geometry should scale with screen resolution, not scene complexity. That means constant time in terms of scene complexity and constant time means level of detail.
雖然沒有完美實踐過,不過通常來說渲染幾何體的開銷是與屏幕分辨率正相關的,而不是場景複雜度。這意味著在(不同)場景複雜度方面的恆定時間,而恆定時間意味著採用LOD。
*這裡再次突出了這個方案的重點,就是“逐像素”或者規模與像素正相關。
4 LOD的構建

集群層級
- 決定LOD基於一個集群基礎方案
- 構建LOD層級:最簡單的就是樹狀集群;父節點是它們子節點的簡化版
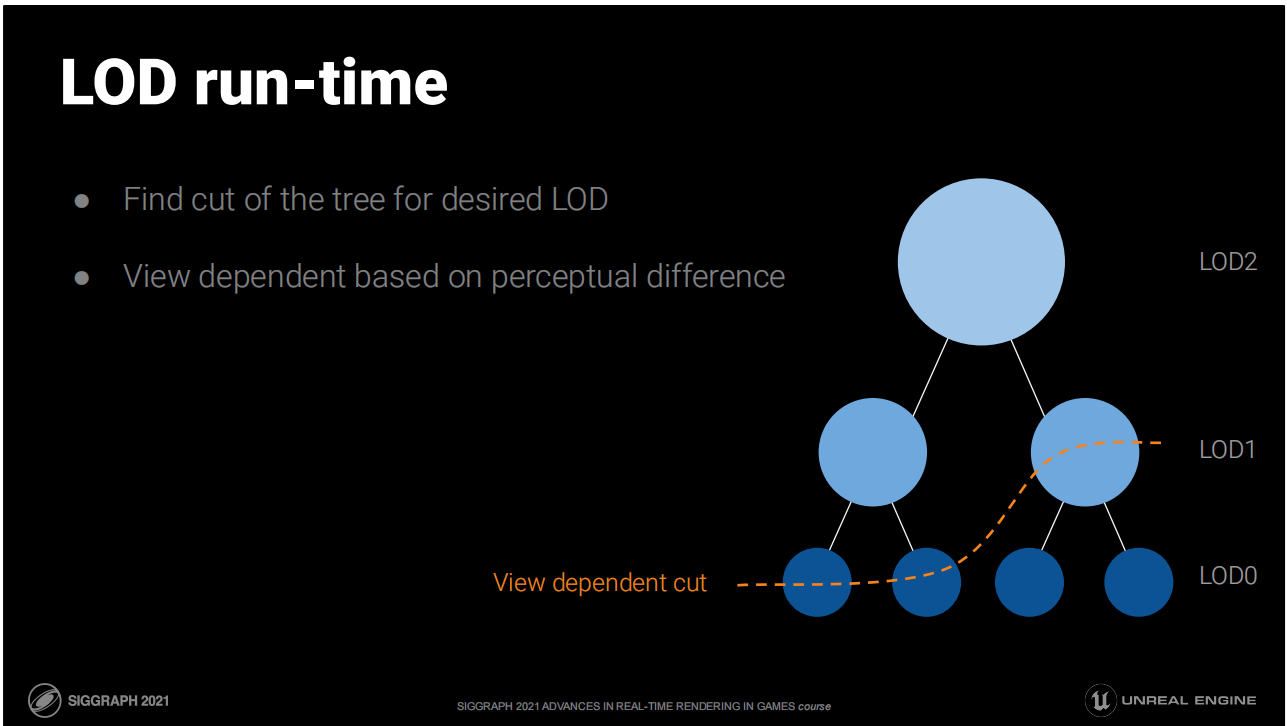
LOD運行時
- 找到樹中目標LOD的切片(這意味著同一網格的不同部件可能有不同LOD)
- 基於視點通過感知差異(屏幕空間的投影容差範圍)來決定切面

流式加載
- 整個樹不需要同時都在內存中
- 可以標記出樹的部分切面作為葉子節點,丟棄其它節點
- 在渲染時按需請求數據——像虛擬紋理一樣
*這裡可以說是虛擬幾何體方案的核心思想之一——破除傳統的一些綁定上的限制,按需加載渲染。

LOD裂開問題
- 如果每個集群都與相鄰物體無關的來決定LOD,就可能導致開裂問題
- 不成熟的方案:在網格簡化的過程中鎖定共享的邊界;不相關的集群將始終在邊界處相合
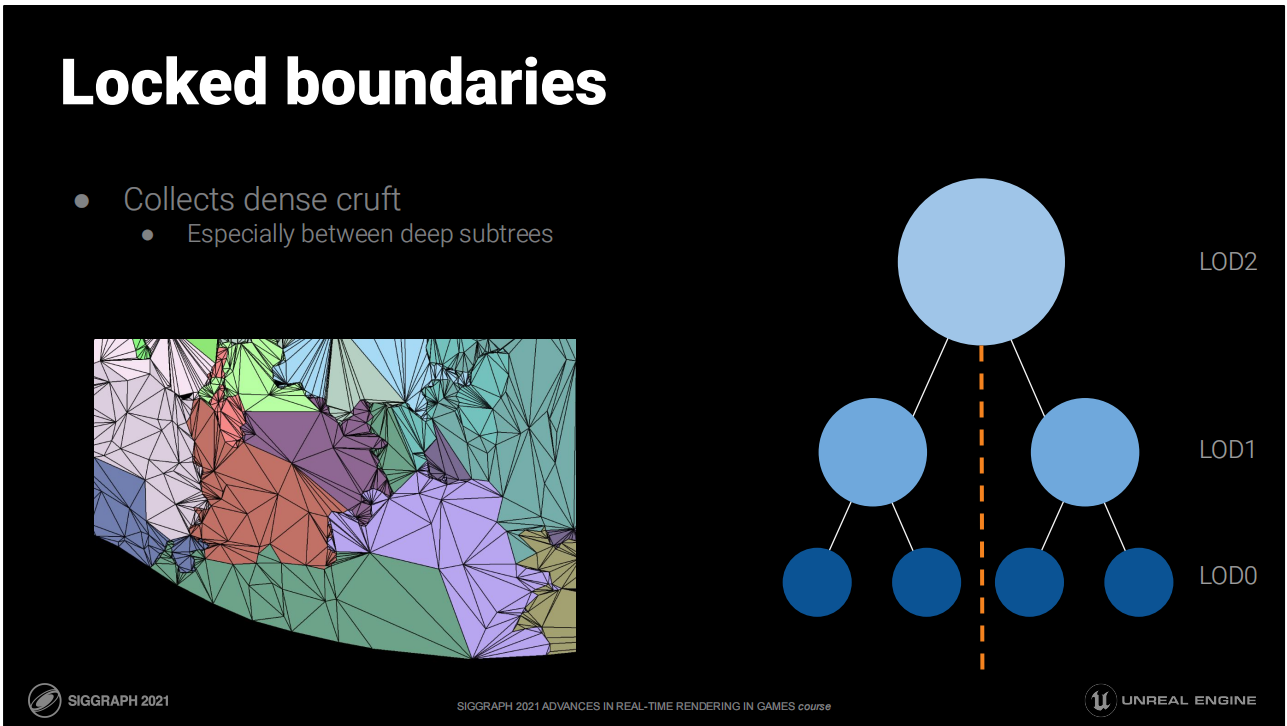
鎖定的邊界
*如圖所示,這種限制會帶來邊界不整齊的問題。
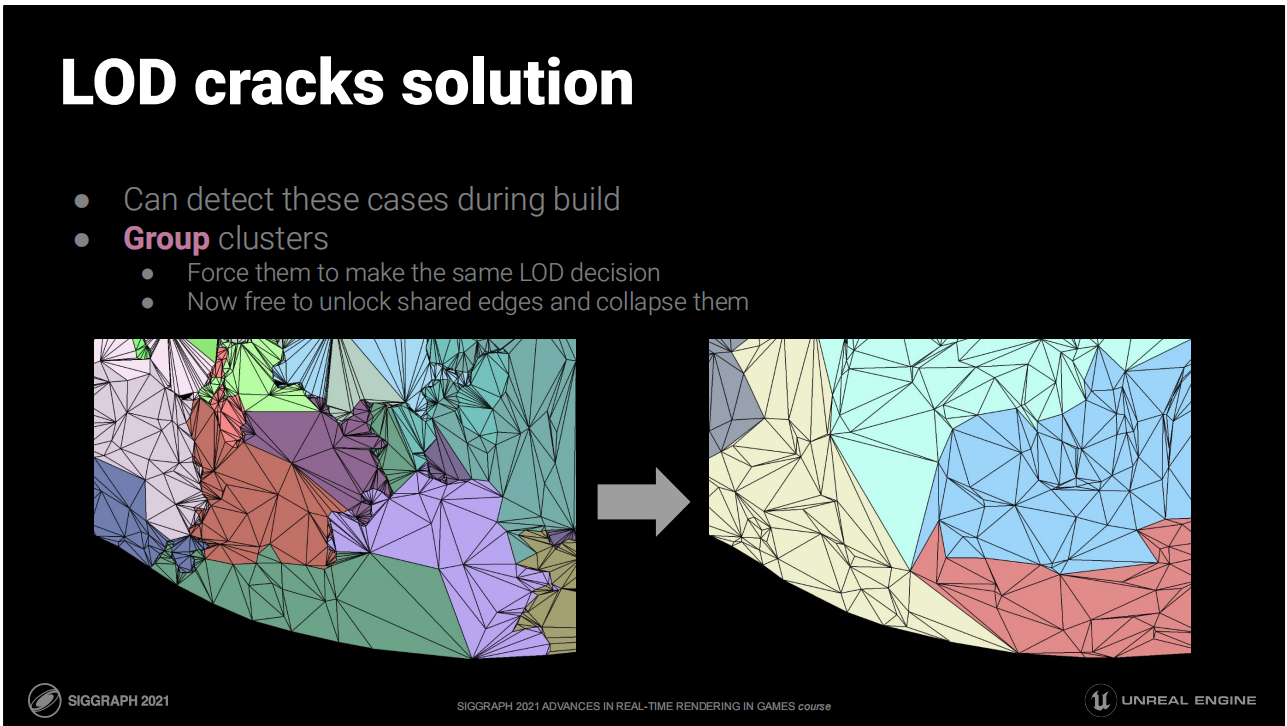
LOD裂開的解決方案
- 可以在構建時探測出這類情況
- 將集群分組:強制它們採用同樣的LOD;現在就可以自由解鎖共享的邊緣或使之塌陷了
*原文中還以實例演示了這一方案的基本思路,並對比了其它潛在的解決LOD裂開的方案。篇幅原因這裡不展開了,有興趣可以去看文末鏈接。
5 資源構建過程

構建操作
將原始的三角形集群化。當集群數大於1時:
- 將集群分組以清除它們組內的共享邊界
- 將同組的三角形融合到共享列表中
- 簡化至一半三角形數量
- 將簡化後的三角形拆分並歸入新集群(128個三角形一組)
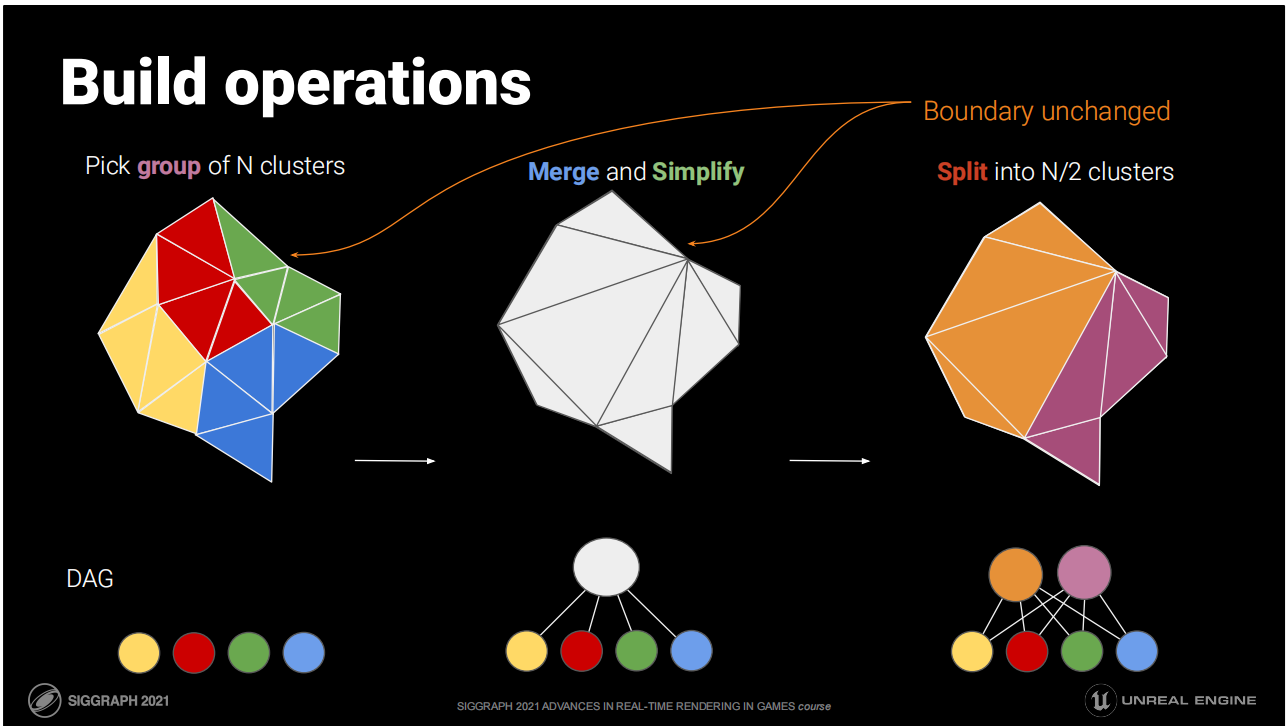
構建操作
*圖中演示了這一構建歸納的步驟,最終的得到的數據結構是一個DAG(Directed Acyclic Graph 有向無環圖,這裡的“圖”是一種數據結構)。
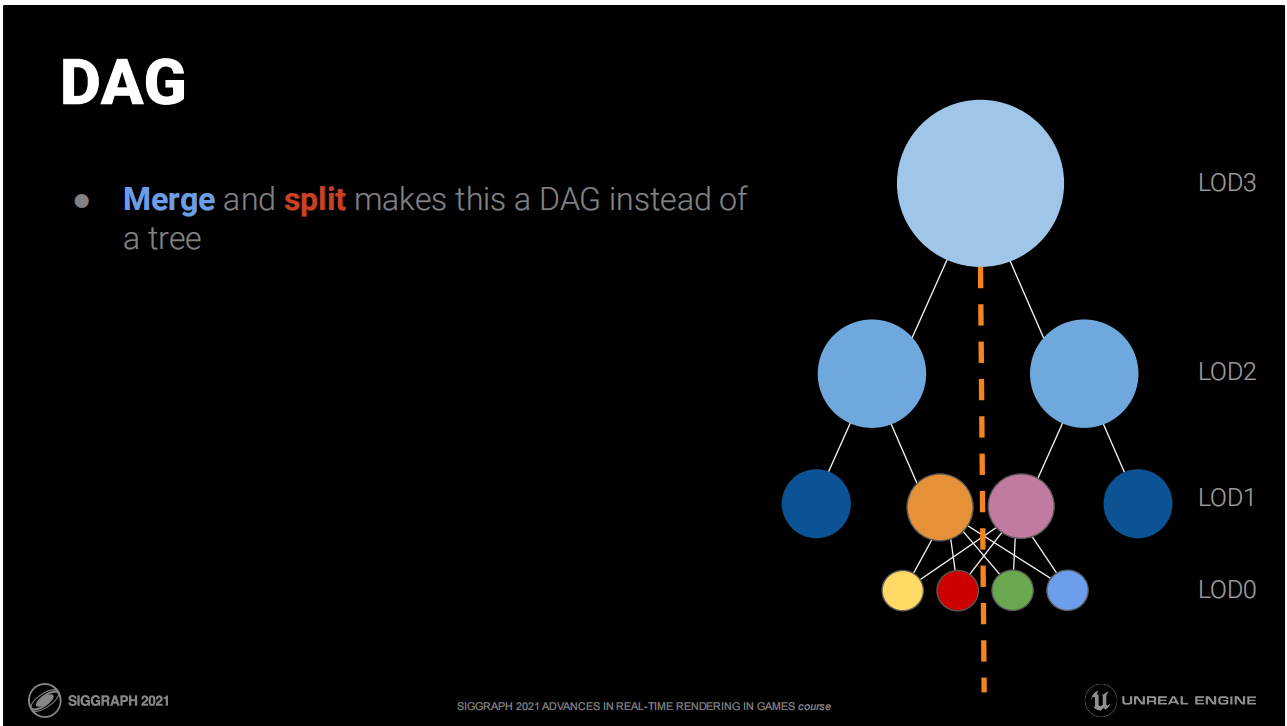
融合和拆分操作使這個結構是一個DAG而不是樹。

DAG:哪些集群分為一組
將有著最多共享邊緣的集群分為一組——更少邊緣等於更少鎖定邊緣。
這類問題被稱為圖分割問題。圖分割可以用來最小化邊緣切割的消耗:
- 圖節點=集群
- 圖邊緣=通過直接相連的三角形連接集群
- 圖邊緣權重=共享三角形邊緣的數量
- 對於空間上閉合的集群需要額外的圖邊緣——為“孤島”添加空間信息
最小化圖邊緣切割等於鎖定最少邊緣。可以使用METIS庫來輔助(METIS是一款高效數據分割與圖劃分工具)。

初始的集群
需要優化很多變量:
- 為了剔除的效果,需要儘量少擴張集群的包圍盒
- 集群中三角形的數量需要儘量接近,但不超過128個以符合光柵化過程
- 基於原始shader的限制,頂點的數量還是不能超限
- 最小化集群的外界邊數,以減少對網格簡化過程的限制
*這部分直接翻譯自解說稿,因為比頁內的內容更清楚一些。

圖分割
- 由於不可能優化所有方面,因此選擇了兩個相關的維度進行優化,並期待其它方面最終能有效:優化集群邊緣邊的數量及每個集群三角形的數量。
- 這和之前集群分組面臨的是一樣的問題——圖是網格的對偶。
- 對於劃分的上限需要嚴格限制:圖分割算法並不能保證這一點,因此需要通過適當的放鬆條件和替代方案等強制其生效。

*最終發現初始化三角形集群和拆分三角形集群是在做同一件事。

網格簡化
- 邊緣塌陷(指維度上合併摺疊)
- 選擇誤差最小的邊緣開始
- 誤差估計採用被稱為QEM(Quadric Error Metric)的方法
- 在優化新頂點的位置使盡量引入最小誤差
- 整體方案是高度精煉和改進的
- 需要返回誤差估計——否則後續在投射到屏幕空間時就會導致像素誤差,而這是最困難的部分
*後面分享者還提到了一些具體的困難,例如儘管可以用啟發式分析算法來分析像素誤差,有時候對於具體的法線、材質、頂點顏色等是無法拋開其應用場合(或重要程度)來保證結果的,但這些在網格簡化的過程中並不全部知道。
*後面還有幾頁介紹了誤差分析的一些細節問題,以及在預過濾方面暫時不支持(未來想引入)的一些課題。篇幅原因也不展開了,有興趣的可以去看原文。
結語
之前讀的《漫威蜘蛛俠2》的GDC分享中,Insomiac對於自動化的處理兩層建築LOD都已經用盡了各種複雜的組合方案;而這裡UE5要提供的是一套普適的應對高清3D美術資產的方案,顯然是更復雜維度更多的方案,裡面引用的大量前人的技術積累讓人看起來頭暈目眩。
總結來說,UE5的多邊形魔法主要來自全新的GPU驅動管線、渲染後期步驟的逐像素流程以及定製化的網格LOD結構——這部分主要涉及了他們整套管線設計方案的方方面面,很細緻也很有革新性。尤其是LOD整體方案,確實如他們所說是一個“不斷精進”的過程。
直到今年開始,一些後立項的高清渲染遊戲例如《影之刃:零》才開始逐步放出消息,回頭算算估計也是和UE5推出幾乎同步開始開發的;以後這類只面向更高畫質的大型3A遊戲可能會逐漸多起來,但這需要UE5的這套新技術框架經得住更多商業的考驗。
最容易想到的兩個問題,一個是這套機制它要能自己穩定運行,即減少引入BUG和無法人工補救的問題;另一個方面就是它有相對更高的硬件性能要求,因為它的設計初衷就是面向高質量3A項目的,實際上從玩家的角度看來,這個時代的硬件設備可能還沒有準備好迎接它。
下一篇文章中會覆蓋他們提到的運行時的一些細節,看看有了這些框架和數據結構後運行時又有哪些新課題。
最後是一些資料鏈接:
Nanite A Deep Dive 原文地址
之前的數據結構方案 Quick-VDR 介紹
之前的數據結構方案Batched Multi-triangulation的論文頁