從桌遊機制角度看《漫威終極逆轉》（Marvel Snap）-3樓貓

《Marvel Snap》是爐石之父Ben Brode在離開暴雪後成立公司Second Dinner的第一部作品，曾斬獲2022TGA年度最佳手遊獎。身為一名毛線桌遊玩家，我在這款遊戲中看到許多經典桌遊機制的影子，當我聽到其國服《漫威終極逆轉》就快要上線時，便有了寫這篇文章的想法。

總覽

正文約5000字。對於遊戲名的書寫，有時寫作帶書名號的“《漫威終極逆轉》”，有時寫作不帶書名號的“終極逆轉”。文章中有大量個人觀點，不喜勿噴，歡迎討論和補充。

法力值系統——逐回合增長的行動點

法力值系統在卡牌遊戲中並不少見，它的本源是行動點（Action Points）機制，玩家每回合擁有一些行動點，可用於不同的行動。

在TCG/CCG遊戲中，法力值系統並非必需。使用法力值系統的例子是《萬智牌》和《爐石戰記》，不使用法力值系統的例子是《遊戲王》和《昆特牌》。

為卡牌賦予法力值消耗的好處在於，卡牌的設計空間增大了，你可以設計一張2費4點效果的牌，和一張3費6點效果的牌，由於它們的平均價值相等，可以說這兩張牌是大致平衡的（當然，實際情況要根據玩家數據再平衡）。這就自然引出了卡牌的價值模型，我們通常會規定一張白板牌每點費用的標準價值，然後根據添加的額外效果的價值來調整。在《漫威終極逆轉》中，這個模型大約是1費2戰力，所有卡的實際強度分佈在y=2x這條直線的兩側。我們不禁要問，為什麼是y=2x而不是y=x或y=3x？y=x顯然不夠好，它限制了卡牌的設計空間，卡牌的額外效果需要至少為1費的價值，而不能是0.5費，此外還限制了0費卡的設計；至於y=3x，它確實提供了更豐富的設計空間和更精細的平衡調整尺度，但似乎不如從y=x到y=2x來得明顯？再加上游戲本身的定位是休閒向的，為了不引入過多的複雜度，所以採用了較簡的設計（這一點我沒有很有說服力的說法，權當拋磚引玉，歡迎各位在評論區討論）。

誒，等一下，玩得久的朋友應該已經注意到了，《漫威終極逆轉》的1費牌有一點特殊：有很多1費兩點戰力的牌，還具有正面的額外效果，它們的平均價值明顯大於2點戰力，介於3-4戰力之間，逼近2費卡的價值，我們可以稱之為“1費超模現象”（事實上，在《爐石戰記》中也有類似的現象）。個人對這種現象的解釋是：1費卡是全遊戲戰力最低的卡，它打不過任何費用比它高的卡（其實0費卡也是如此，但是0費卡可以免費打出，這是它獨有的優勢），而手牌是有限的，如果打出兩張1費牌的價值只與1張2費牌的價值相等，那麼就淨虧一張手牌，鑑於此，將1費卡的價值做適當的提升，才能在實際勝率上做到平衡。

還有一個想要討論的問題是法力值的增長。在採用法力值系統的TCG/CCG遊戲中，幾乎全都設計成法力值隨回合增長（《爐石戰記》為自然增長，《萬智牌》為每回合打出至多一張地牌，地牌每回合產出一點對應的元素力），這是為什麼？剛才我們已經討論過，1點法力值產生的價值是相對固定的，那麼隨回合增長的法力值就意味著每回合都能比上一回合打出更高的價值。這到底有什麼好處呢？我們來考慮這樣一個數學模型：有一個使用行動點機制的遊戲，行動的價值與所消耗的行動點成正比，遊戲進行n個回合，並且行動點a隨回合數x變化的規律為a=g(x)，我們來研究在消耗所有行動點的情況下，第x回合中玩家行動的價值佔整場遊戲他行動的總價值之比V隨x變化的規律V=f(x)。

第一種情況，每回合玩家擁有固定的行動點，即a=m，m為常數。此時f(x)=1/n；

第二種情況，行動點隨回合數自然增長，即a=x，此時f(x)=2x/n(n+1).

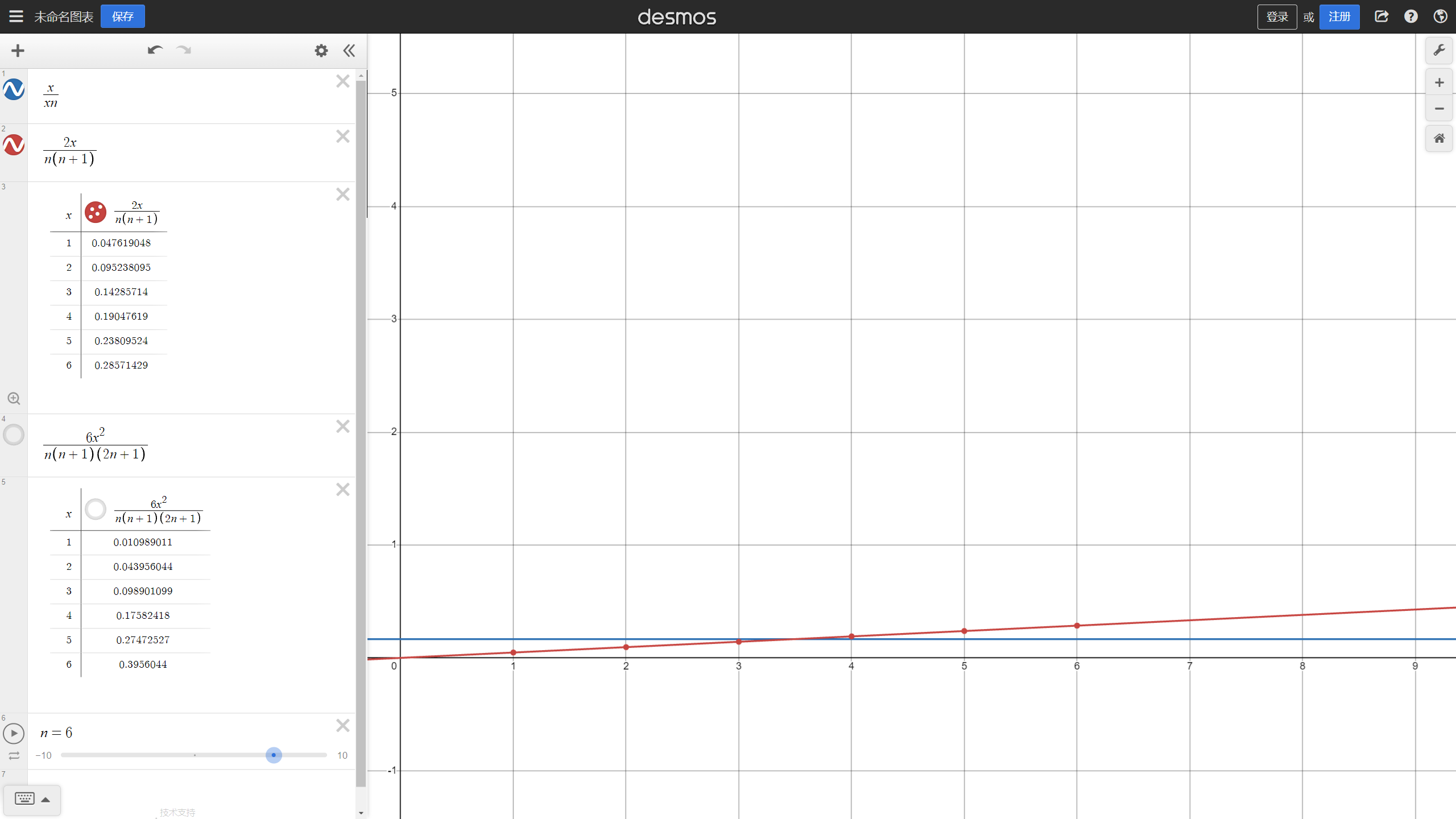
藍色曲線為情況一，紅色曲線為情況二

f(x)的含義是什麼？它表示的是玩家在各個回合影響戰局的能力，因為一般認為，玩家擁有的行動點越多，他影響戰局的能力就越強大。可以看到，情況一中玩家影響戰局的能力是恆定的，情況二中玩家影響戰局的能力隨回合數線性增長。個人認為情況二能帶來更引人入勝的體驗曲線，一場早早進入垃圾時間的對局遠不如一場膠著到最後的對局精彩，而行動點的增長有利於將懸念留到對局結束。

共用回合制——同步行動選擇

不玩桌遊的朋友應該是在終極逆轉中第一次見到這個機制。官方的宣傳口徑為“共用回合制”，它實際上就是桌遊機制中的同步行動選擇（Simultaneous Action Selection）。與你拍一我拍一的回合制不同，同步行動選擇讓玩家在同一回合秘密地做出決定，然後同時揭曉。

這個機制的優點之一在於，每一回合所有玩家都參與決策，無需等待他人的回合，幾乎消滅了downtime（玩家的不活躍時間）。個人認為這一機制的出現對於多玩家回合制遊戲是革命性的，它大幅縮短了一局遊戲的時間，提升了玩家的決策密度。此機制與《漫威終極逆轉》的定位高度契合。如果要問終極逆轉輕量化最大的功臣是誰，這個機制是當仁不讓的。

這個機制還有另一個優點：規避先後手平衡問題。在先後手回合制的卡牌遊戲中，先後手的勝率往往存在差距（一般是先手優勢），而這種差距是不太好平衡的，比方說你讓後手比先手多一張起始手牌，發現先手勝率還是略高於後手，但是當你讓後手多兩張起始手牌時，後手勝率可能反而高於先手了。在桌遊中還有一些其它的解決方案，比如傳遞起始玩家（Turn Order: Progressive），基於情況的回合順序（Turn Order: Stat-Based），時間軸（Turn Order: Time Track，這也是個人比較喜歡的一個機制）。而同步行動選擇引入了最少的認知負擔，且具有優雅的對稱性。在《漫威終極逆轉》中，僅雙方場面平局時的翻牌順序是隨機的（並且誰先翻牌會告訴玩家），而大部分時候，遊戲會有領先的一方，領先者先手翻牌（這一點其實有點像基於情況的回合順序）。

不得不說的是，電子媒介給予了這個機制巨大的潛力。我們可以想象一下，如果《漫威終極逆轉》是個桌遊，共用回合制運作起來是什麼樣的。首先，雙方各需要一個屏風，以遮擋本回合擺放卡牌的數量及位置，為了不遮擋戰場導致引入多餘的記憶要素，需要設置一個出牌區，屏風僅遮擋出牌區；此外還需要一些標有數字的標記，用於記錄本回合卡牌放置的順序（不然玩家就可以在屏風揭開後改變牌序）；雙方還各需要一張撤退卡，在想要“稍後撤退”時放置於屏風後；這還是沒有考慮到移動的情況，如果要處理移動機制，還需要一些指示移動的標記，同樣放在屏風後以防止玩家改變主意......可以預見到，實體版的結算是非常繁瑣的。可以說，在電子媒介上通過網絡連接進行對戰，使這款遊戲走向大眾成為了可能。

個人認為，同步行動選擇是對回合制的一次進化，而電子媒介將使該機制得以發揚光大。

戰力分配——田忌賽馬

很抱歉我沒有為 Force Commitment 這個機制找到一個合適的直譯，不過我們中國人都很熟悉田忌賽馬的故事，那麼姑且就以這個典故作為此機制的意譯。需要注意的是，雖然歷史上的田忌賽馬是共用回合制的，桌遊中的田忌賽馬和同步行動選擇卻沒有必然聯繫。

在田忌賽馬遊戲中，玩家如果能判斷出對手的上、中、下等馬分別在哪一路，他就具有了信息優勢。而在共用回合制下，正確的讀牌在信息差上相當於把遊戲變成了輪流行動。

田忌賽馬機制在《漫威終極逆轉》中作為核心玩法存在，遊戲採用了最簡單的3路2勝制。如果你在兩路的戰力比對手大，你就贏了。這個機制有一些邊緣情況：當有一路為平局時，比拼雙方的總戰力，高者贏；如果總戰力也平局，那麼本場遊戲就是平局。除了影響最終的勝負，每回合戰力的結果都會影響翻牌順序，即領先者先翻牌，這就引入了一些高級策略。遊戲中有很多針對對手特定的牌有著強大反制效果的牌（稱為仇恨牌），而這些牌對翻牌的先後手往往有嚴格的要求。為了使仇恨牌發揮最大效果，往往需要提前規劃手牌，甚至活用地點效果來搶先手、控後手。

地點——可變起始設置

可變起始設置（Variable Set-up）是一個概念非常廣的機制，它的含義是每把遊戲開始時的狀態各不相同。在桌遊中，這是一個增加重開性（重玩價值）的機制。

《漫威終極逆轉》由於輕量化設計，需要豐富同一卡組在不同對局中的差異化體驗。既然遊戲中有三個放置卡牌的地點，那麼就為這些地點添加不同的特殊效果，玩家需要根據每局的地點，因地制宜地制定策略。這一做法優雅且自然，沒有引入多餘的複雜度。

地點

關於地點有個機制細節，3個地點是隨1、2、3回合逐回合揭曉的，而非一開始就全部展示給玩家，這一做法與德州撲克是吻合的。個人認為，這是為了達成一種緊湊的遊戲體驗。我們知道決策依賴於信息，而新的信息可能影響決策。而一次給出的信息量過大，會導致玩家的認知負擔。所以，最好以最少量的新信息實現對決策的影響。既然每回合僅揭示一個地點就足以改變玩家在當前回合的決策，那就不妨把地點信息分割成更小的3份，逐步給出。

Snap——下注與打賭

從遊戲名就可以看出，Snap是這個遊戲的靈魂機制。乍一看，Snap跟核心玩法戰力分配沒什麼聯繫，實際上也確實沒有聯繫（除了少數卡牌會對snap做出響應）。那麼為什麼還要加入這個機制呢？讓我們從德州撲克聊起。

我們知道，在德州撲克中，如果你認為沒有人的牌型比你大，你可以加註（Raise）來贏得更多的籌碼；如果你認為自己不可能大過別人，你可以早早棄牌（Fold）撤退；如果你想靜觀其變，可以跟注（Call）或過牌（Check），在不添加額外賭注的情況下留在場上。發現了嗎，《漫威終極逆轉》的Snap機制與德州撲克高度相似，如果雙方都不Snap，就相當於Check，如果一方Snap了，就相當於Raise，另一方可以選擇撤退（Fold）、留下（Call）或 Snap（Raise）。二者有如此高的相似性是因為它們都有下注與打賭（Betting and Bluffing）機制。

Snap在遊戲中究竟起到了什麼作用？我們設想一個沒有Snap機制的《漫威終極逆轉》，每一把遊戲都是獲勝方從失敗方處獲取1個魔方（排位分），那麼可能你辛辛苦苦運營贏下的1分，在下一局會被運氣因素（比如卡組剋制，比如陰間地點）送回去。此外，上分效率將和卡組勝率嚴格成正比，而實現各個卡組的勝率平衡是一件非常困難的事情，也就是說，只有幾套勝率寡頭的卡組會成為主流。而在現實的《漫威終極逆轉》中，天梯的環境是百花齊放的；運氣因素雖然影響大，卻沒有飽受詬病。這些很大程度上要歸功於Snap機制。第一，Snap為提前撤退賦予了更大的意義。當出現明顯劣勢，對手又Snap時，“世界未亡，死不投降”就不再成立，撤退成為了及時止損的上計；遊戲結束時的自動翻倍更是讓玩家需要仔細判斷局勢，決定去留。第二，Snap使得卡組勝率不再是上分效率的直接影響因素，取而代之的是場均魔方數，這兩者有很大的差別。一般來說，卡組勝率比場均魔方數更能代表卡組強度，但勝率低不代表場均魔方數低，舉例來說，如果一個卡組平均5把輸3把，勝率只有可憐的40%，但是那3把都是提前撤退，輸1個魔方，而贏的2把都在無人Snap的情況下打到了最後，各贏2個魔方，這樣一來此卡組的場均魔方數就是(2×2-1×3)/5=0.2，反而可以上分。於是，由於場均魔方數足夠高（這個“足夠高”是玩家自己的主觀判斷），一些原本勝率不在第一梯隊的卡組，甚至是娛樂卡組也可以在環境中有一席之地。再加上終極逆轉中天梯的賽制是一局定勝負（BO1），一些不常見但是藏在最後一回合打出可以陰人的牌往往能讓對手防不勝防，甚至送出8分。就這樣，Snap的存在極大地優化了排位機制，使天梯環境百花齊放。

既然Snap和遊戲本身的核心玩法是可解耦的，我們甚至可以期望，類似的下注與打賭機制可以結合到以後的卡牌對戰遊戲中，成為一種通用的優化排位機制、使環境多樣化的解決方案。

卡組預構築

我們總是把TCG/CCG（集換式卡牌遊戲/收集式卡牌遊戲）和卡組預構築（

Deck Construction）綁定在一起，但實際上這兩個術語描述的並非同一件事，前者表示的是卡牌的獲取方式（開包、交易等），後者表示的是卡組的構成規則，或者說，賽制。

卡組預構築遊戲通常會對卡組的卡牌總數和同名卡牌數做出限制。而《漫威終極逆轉》對CCG做了最大程度的簡化，一套卡組只有12張牌，且不能出現同名牌。起始手牌為3張，每個回合開始時抽一張牌，這意味著一局遊戲中玩家通常能抽到9張牌，所以終極逆轉的卡組穩定性是較高的。這也是遊戲幾乎沒有抽牌卡，且沒有手牌調度（更換起始手牌）的部分原因。

在法力值系統下，卡組構築需要考慮法力曲線，簡稱曲線。曲線是指卡組中卡牌費用的分佈。曲線既不能過高（高費牌過多）也不能過低（低費牌過多），一個合理的曲線能在對局中利用好幾乎每一點法力值。曲線一定程度反映了卡組形態，比如低曲線的卡組常被稱為快攻、動物園，高曲線的卡組常被稱為中速、控制。當然卡組形態不是由法力曲線唯一決定的。但從卡組的曲線中的確能看出其對各回合的規劃。

雖然遊戲只有一種卡牌類型（即所有牌都是“隨從牌”），但卻具有豐富的卡牌效果。從觸發方式上，目前有揭示（入場效果）、持續（光環效果）、移動（主動效果，未來還會加入“激活”關鍵詞）和大量非揭示的觸發器效果（這些效果在遊戲中沒有對應的關鍵詞，包括但不限於被摧毀時、放置其它卡牌時、回合開始時）。

有趣的是，《漫威終極逆轉》中有著大量的仇恨牌。仇恨牌指的是針對特定卡牌有極強的反制效果的牌。比如科斯莫剋制揭示牌，女巫師剋制持續牌，尚氣剋制大哥（王牌獵人），齊爾蒙格剋制所有1費牌，鎧剋制摧毀牌（大哥卡組甚至可以帶一張鎧來反制尚氣）。這些仇恨牌不僅有著防止環境崩潰的作用，還與Snap機制結合得很好，在最後一回合打出仇恨牌往往能起到出奇制勝的效果，從而吃到大分；而優勢被對手Snap時，也可以嘗試讀出對手有什麼仇恨牌可以翻盤，並進行第二層博弈。