从桌游机制角度看《漫威终极逆转》（Marvel Snap）-3楼猫

《Marvel Snap》是炉石之父Ben Brode在离开暴雪后成立公司Second Dinner的第一部作品，曾斩获2022TGA年度最佳手游奖。身为一名毛线桌游玩家，我在这款游戏中看到许多经典桌游机制的影子，当我听到其国服《漫威终极逆转》就快要上线时，便有了写这篇文章的想法。

总览

正文约5000字。对于游戏名的书写，有时写作带书名号的“《漫威终极逆转》”，有时写作不带书名号的“终极逆转”。文章中有大量个人观点，不喜勿喷，欢迎讨论和补充。

法力值系统——逐回合增长的行动点

法力值系统在卡牌游戏中并不少见，它的本源是行动点（Action Points）机制，玩家每回合拥有一些行动点，可用于不同的行动。

在TCG/CCG游戏中，法力值系统并非必需。使用法力值系统的例子是《万智牌》和《炉石传说》，不使用法力值系统的例子是《游戏王》和《昆特牌》。

为卡牌赋予法力值消耗的好处在于，卡牌的设计空间增大了，你可以设计一张2费4点效果的牌，和一张3费6点效果的牌，由于它们的平均价值相等，可以说这两张牌是大致平衡的（当然，实际情况要根据玩家数据再平衡）。这就自然引出了卡牌的价值模型，我们通常会规定一张白板牌每点费用的标准价值，然后根据添加的额外效果的价值来调整。在《漫威终极逆转》中，这个模型大约是1费2战力，所有卡的实际强度分布在y=2x这条直线的两侧。我们不禁要问，为什么是y=2x而不是y=x或y=3x？y=x显然不够好，它限制了卡牌的设计空间，卡牌的额外效果需要至少为1费的价值，而不能是0.5费，此外还限制了0费卡的设计；至于y=3x，它确实提供了更丰富的设计空间和更精细的平衡调整尺度，但似乎不如从y=x到y=2x来得明显？再加上游戏本身的定位是休闲向的，为了不引入过多的复杂度，所以采用了较简的设计（这一点我没有很有说服力的说法，权当抛砖引玉，欢迎各位在评论区讨论）。

诶，等一下，玩得久的朋友应该已经注意到了，《漫威终极逆转》的1费牌有一点特殊：有很多1费两点战力的牌，还具有正面的额外效果，它们的平均价值明显大于2点战力，介于3-4战力之间，逼近2费卡的价值，我们可以称之为“1费超模现象”（事实上，在《炉石传说》中也有类似的现象）。个人对这种现象的解释是：1费卡是全游戏战力最低的卡，它打不过任何费用比它高的卡（其实0费卡也是如此，但是0费卡可以免费打出，这是它独有的优势），而手牌是有限的，如果打出两张1费牌的价值只与1张2费牌的价值相等，那么就净亏一张手牌，鉴于此，将1费卡的价值做适当的提升，才能在实际胜率上做到平衡。

还有一个想要讨论的问题是法力值的增长。在采用法力值系统的TCG/CCG游戏中，几乎全都设计成法力值随回合增长（《炉石传说》为自然增长，《万智牌》为每回合打出至多一张地牌，地牌每回合产出一点对应的元素力），这是为什么？刚才我们已经讨论过，1点法力值产生的价值是相对固定的，那么随回合增长的法力值就意味着每回合都能比上一回合打出更高的价值。这到底有什么好处呢？我们来考虑这样一个数学模型：有一个使用行动点机制的游戏，行动的价值与所消耗的行动点成正比，游戏进行n个回合，并且行动点a随回合数x变化的规律为a=g(x)，我们来研究在消耗所有行动点的情况下，第x回合中玩家行动的价值占整场游戏他行动的总价值之比V随x变化的规律V=f(x)。

第一种情况，每回合玩家拥有固定的行动点，即a=m，m为常数。此时f(x)=1/n；

第二种情况，行动点随回合数自然增长，即a=x，此时f(x)=2x/n(n+1).

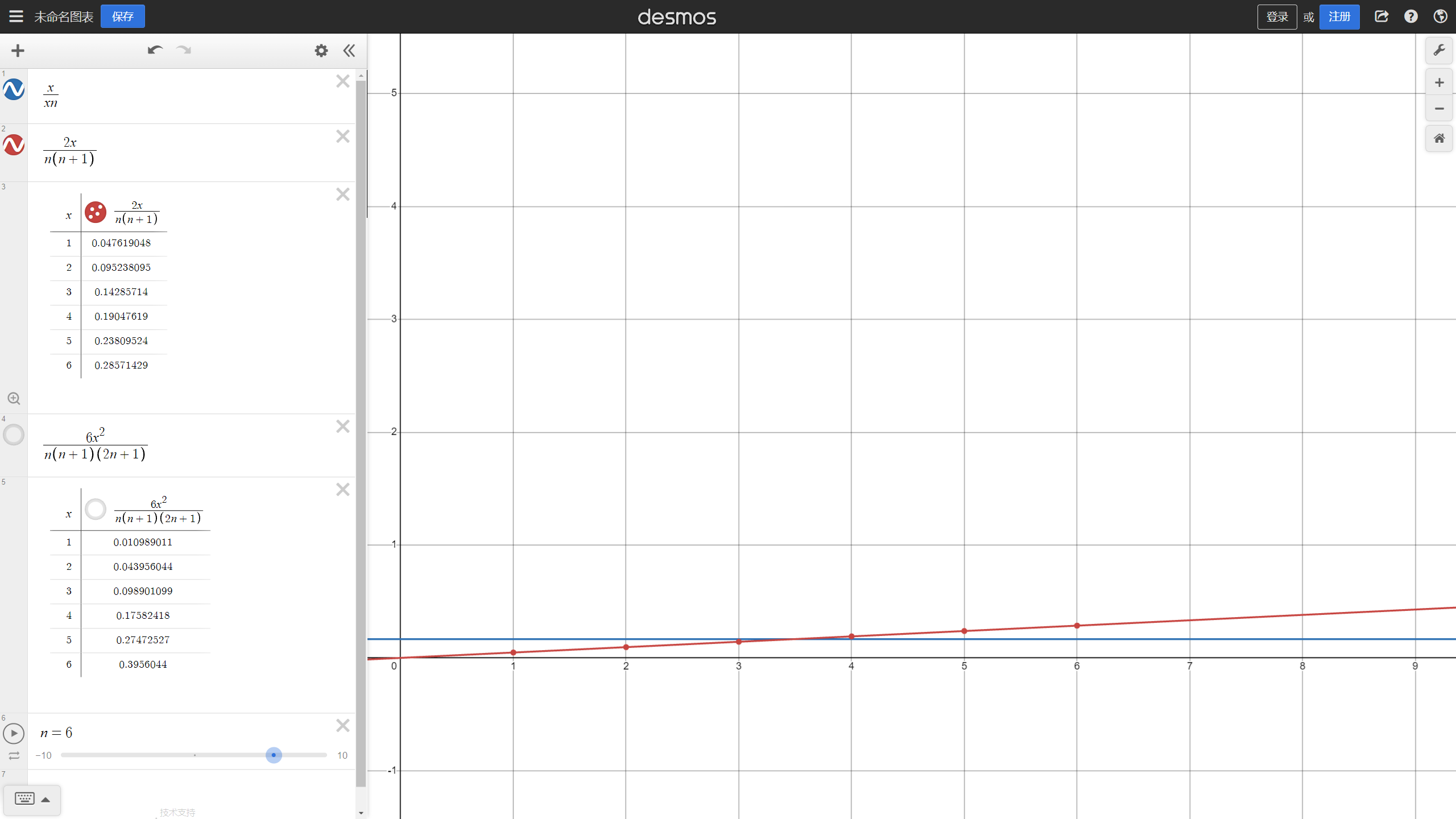
蓝色曲线为情况一，红色曲线为情况二

f(x)的含义是什么？它表示的是玩家在各个回合影响战局的能力，因为一般认为，玩家拥有的行动点越多，他影响战局的能力就越强大。可以看到，情况一中玩家影响战局的能力是恒定的，情况二中玩家影响战局的能力随回合数线性增长。个人认为情况二能带来更引人入胜的体验曲线，一场早早进入垃圾时间的对局远不如一场胶着到最后的对局精彩，而行动点的增长有利于将悬念留到对局结束。

共用回合制——同步行动选择

不玩桌游的朋友应该是在终极逆转中第一次见到这个机制。官方的宣传口径为“共用回合制”，它实际上就是桌游机制中的同步行动选择（Simultaneous Action Selection）。与你拍一我拍一的回合制不同，同步行动选择让玩家在同一回合秘密地做出决定，然后同时揭晓。

这个机制的优点之一在于，每一回合所有玩家都参与决策，无需等待他人的回合，几乎消灭了downtime（玩家的不活跃时间）。个人认为这一机制的出现对于多玩家回合制游戏是革命性的，它大幅缩短了一局游戏的时间，提升了玩家的决策密度。此机制与《漫威终极逆转》的定位高度契合。如果要问终极逆转轻量化最大的功臣是谁，这个机制是当仁不让的。

这个机制还有另一个优点：规避先后手平衡问题。在先后手回合制的卡牌游戏中，先后手的胜率往往存在差距（一般是先手优势），而这种差距是不太好平衡的，比方说你让后手比先手多一张起始手牌，发现先手胜率还是略高于后手，但是当你让后手多两张起始手牌时，后手胜率可能反而高于先手了。在桌游中还有一些其它的解决方案，比如传递起始玩家（Turn Order: Progressive），基于情况的回合顺序（Turn Order: Stat-Based），时间轴（Turn Order: Time Track，这也是个人比较喜欢的一个机制）。而同步行动选择引入了最少的认知负担，且具有优雅的对称性。在《漫威终极逆转》中，仅双方场面平局时的翻牌顺序是随机的（并且谁先翻牌会告诉玩家），而大部分时候，游戏会有领先的一方，领先者先手翻牌（这一点其实有点像基于情况的回合顺序）。

不得不说的是，电子媒介给予了这个机制巨大的潜力。我们可以想象一下，如果《漫威终极逆转》是个桌游，共用回合制运作起来是什么样的。首先，双方各需要一个屏风，以遮挡本回合摆放卡牌的数量及位置，为了不遮挡战场导致引入多余的记忆要素，需要设置一个出牌区，屏风仅遮挡出牌区；此外还需要一些标有数字的标记，用于记录本回合卡牌放置的顺序（不然玩家就可以在屏风揭开后改变牌序）；双方还各需要一张撤退卡，在想要“稍后撤退”时放置于屏风后；这还是没有考虑到移动的情况，如果要处理移动机制，还需要一些指示移动的标记，同样放在屏风后以防止玩家改变主意......可以预见到，实体版的结算是非常繁琐的。可以说，在电子媒介上通过网络连接进行对战，使这款游戏走向大众成为了可能。

个人认为，同步行动选择是对回合制的一次进化，而电子媒介将使该机制得以发扬光大。

战力分配——田忌赛马

很抱歉我没有为 Force Commitment 这个机制找到一个合适的直译，不过我们中国人都很熟悉田忌赛马的故事，那么姑且就以这个典故作为此机制的意译。需要注意的是，虽然历史上的田忌赛马是共用回合制的，桌游中的田忌赛马和同步行动选择却没有必然联系。

在田忌赛马游戏中，玩家如果能判断出对手的上、中、下等马分别在哪一路，他就具有了信息优势。而在共用回合制下，正确的读牌在信息差上相当于把游戏变成了轮流行动。

田忌赛马机制在《漫威终极逆转》中作为核心玩法存在，游戏采用了最简单的3路2胜制。如果你在两路的战力比对手大，你就赢了。这个机制有一些边缘情况：当有一路为平局时，比拼双方的总战力，高者赢；如果总战力也平局，那么本场游戏就是平局。除了影响最终的胜负，每回合战力的结果都会影响翻牌顺序，即领先者先翻牌，这就引入了一些高级策略。游戏中有很多针对对手特定的牌有着强大反制效果的牌（称为仇恨牌），而这些牌对翻牌的先后手往往有严格的要求。为了使仇恨牌发挥最大效果，往往需要提前规划手牌，甚至活用地点效果来抢先手、控后手。

地点——可变起始设置

可变起始设置（Variable Set-up）是一个概念非常广的机制，它的含义是每把游戏开始时的状态各不相同。在桌游中，这是一个增加重开性（重玩价值）的机制。

《漫威终极逆转》由于轻量化设计，需要丰富同一卡组在不同对局中的差异化体验。既然游戏中有三个放置卡牌的地点，那么就为这些地点添加不同的特殊效果，玩家需要根据每局的地点，因地制宜地制定策略。这一做法优雅且自然，没有引入多余的复杂度。

地点

关于地点有个机制细节，3个地点是随1、2、3回合逐回合揭晓的，而非一开始就全部展示给玩家，这一做法与德州扑克是吻合的。个人认为，这是为了达成一种紧凑的游戏体验。我们知道决策依赖于信息，而新的信息可能影响决策。而一次给出的信息量过大，会导致玩家的认知负担。所以，最好以最少量的新信息实现对决策的影响。既然每回合仅揭示一个地点就足以改变玩家在当前回合的决策，那就不妨把地点信息分割成更小的3份，逐步给出。

Snap——下注与打赌

从游戏名就可以看出，Snap是这个游戏的灵魂机制。乍一看，Snap跟核心玩法战力分配没什么联系，实际上也确实没有联系（除了少数卡牌会对snap做出响应）。那么为什么还要加入这个机制呢？让我们从德州扑克聊起。

我们知道，在德州扑克中，如果你认为没有人的牌型比你大，你可以加注（Raise）来赢得更多的筹码；如果你认为自己不可能大过别人，你可以早早弃牌（Fold）撤退；如果你想静观其变，可以跟注（Call）或过牌（Check），在不添加额外赌注的情况下留在场上。发现了吗，《漫威终极逆转》的Snap机制与德州扑克高度相似，如果双方都不Snap，就相当于Check，如果一方Snap了，就相当于Raise，另一方可以选择撤退（Fold）、留下（Call）或 Snap（Raise）。二者有如此高的相似性是因为它们都有下注与打赌（Betting and Bluffing）机制。

Snap在游戏中究竟起到了什么作用？我们设想一个没有Snap机制的《漫威终极逆转》，每一把游戏都是获胜方从失败方处获取1个魔方（排位分），那么可能你辛辛苦苦运营赢下的1分，在下一局会被运气因素（比如卡组克制，比如阴间地点）送回去。此外，上分效率将和卡组胜率严格成正比，而实现各个卡组的胜率平衡是一件非常困难的事情，也就是说，只有几套胜率寡头的卡组会成为主流。而在现实的《漫威终极逆转》中，天梯的环境是百花齐放的；运气因素虽然影响大，却没有饱受诟病。这些很大程度上要归功于Snap机制。第一，Snap为提前撤退赋予了更大的意义。当出现明显劣势，对手又Snap时，“世界未亡，死不投降”就不再成立，撤退成为了及时止损的上计；游戏结束时的自动翻倍更是让玩家需要仔细判断局势，决定去留。第二，Snap使得卡组胜率不再是上分效率的直接影响因素，取而代之的是场均魔方数，这两者有很大的差别。一般来说，卡组胜率比场均魔方数更能代表卡组强度，但胜率低不代表场均魔方数低，举例来说，如果一个卡组平均5把输3把，胜率只有可怜的40%，但是那3把都是提前撤退，输1个魔方，而赢的2把都在无人Snap的情况下打到了最后，各赢2个魔方，这样一来此卡组的场均魔方数就是(2×2-1×3)/5=0.2，反而可以上分。于是，由于场均魔方数足够高（这个“足够高”是玩家自己的主观判断），一些原本胜率不在第一梯队的卡组，甚至是娱乐卡组也可以在环境中有一席之地。再加上终极逆转中天梯的赛制是一局定胜负（BO1），一些不常见但是藏在最后一回合打出可以阴人的牌往往能让对手防不胜防，甚至送出8分。就这样，Snap的存在极大地优化了排位机制，使天梯环境百花齐放。

既然Snap和游戏本身的核心玩法是可解耦的，我们甚至可以期望，类似的下注与打赌机制可以结合到以后的卡牌对战游戏中，成为一种通用的优化排位机制、使环境多样化的解决方案。

卡组预构筑

我们总是把TCG/CCG（集换式卡牌游戏/收集式卡牌游戏）和卡组预构筑（

Deck Construction）绑定在一起，但实际上这两个术语描述的并非同一件事，前者表示的是卡牌的获取方式（开包、交易等），后者表示的是卡组的构成规则，或者说，赛制。

卡组预构筑游戏通常会对卡组的卡牌总数和同名卡牌数做出限制。而《漫威终极逆转》对CCG做了最大程度的简化，一套卡组只有12张牌，且不能出现同名牌。起始手牌为3张，每个回合开始时抽一张牌，这意味着一局游戏中玩家通常能抽到9张牌，所以终极逆转的卡组稳定性是较高的。这也是游戏几乎没有抽牌卡，且没有手牌调度（更换起始手牌）的部分原因。

在法力值系统下，卡组构筑需要考虑法力曲线，简称曲线。曲线是指卡组中卡牌费用的分布。曲线既不能过高（高费牌过多）也不能过低（低费牌过多），一个合理的曲线能在对局中利用好几乎每一点法力值。曲线一定程度反映了卡组形态，比如低曲线的卡组常被称为快攻、动物园，高曲线的卡组常被称为中速、控制。当然卡组形态不是由法力曲线唯一决定的。但从卡组的曲线中的确能看出其对各回合的规划。

虽然游戏只有一种卡牌类型（即所有牌都是“随从牌”），但却具有丰富的卡牌效果。从触发方式上，目前有揭示（入场效果）、持续（光环效果）、移动（主动效果，未来还会加入“激活”关键词）和大量非揭示的触发器效果（这些效果在游戏中没有对应的关键词，包括但不限于被摧毁时、放置其它卡牌时、回合开始时）。

有趣的是，《漫威终极逆转》中有着大量的仇恨牌。仇恨牌指的是针对特定卡牌有极强的反制效果的牌。比如科斯莫克制揭示牌，女巫师克制持续牌，尚气克制大哥（王牌猎人），齐尔蒙格克制所有1费牌，铠克制摧毁牌（大哥卡组甚至可以带一张铠来反制尚气）。这些仇恨牌不仅有着防止环境崩溃的作用，还与Snap机制结合得很好，在最后一回合打出仇恨牌往往能起到出奇制胜的效果，从而吃到大分；而优势被对手Snap时，也可以尝试读出对手有什么仇恨牌可以翻盘，并进行第二层博弈。