引
最終幻想7重製版使用“湍流火焰”與“逃離混沌”的前章標題呼應,死亡擱淺的非牛頓流體焦油又如何模擬。Haar小波重構出Haar的移動城堡,肯·柏林拿下奧斯卡技術成就獎,Daubechies太強以至理解不能。最終只是實現這樣的效果:分形湍流火焰面
Haar的移動城堡?
或蒸汽朋克風格的鋸齒火焰面(結合麥克斯韋彈性齒輪惰輪電磁場模型,從底層原理出發構建“純齒輪的蒸汽朋克”)
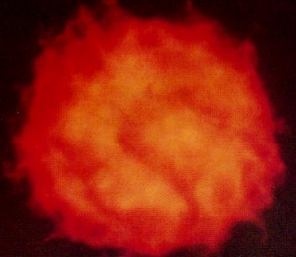
粘性焦油麵效果
最終幻想7重製版,是逃離混沌還是踏入混沌的“湍流火焰”?

計算機圖形也要與修拉和梵高一決高下
序
What I cannot create, I do not understand.
Richard Feynman
1 概述
在最終幻想7重製版(Final Fantasy VII Remake,SQUARE ENIX 2020)最終決戰前、命運的岔路口處,剛剛經歷第17章名為“逃離混沌(Deliverance from Chaos)”的主角團們,不得不再次踏入象徵混沌的“湍流火焰”,非常巧妙的呼應(當然這裡並非真的火焰,只是具有湍流火焰的流動特徵)。在死亡擱淺(Death Stranding, Kojima Project 2019)中,焦油作為冥灘出現在現實世界的副產物之一,也屬於死亡擱淺世界觀下的標誌性物質,它的高粘性從遊戲中也能略窺一二。

“藝術就是爆炸”,爆炸伴隨燃燒。它們都是各種娛樂作品裡的常客,也多是作品體驗過程中的高峰。與水體模擬類似,火焰模擬在計算機圖形學和電子遊戲、影視特效製作中必不可少。20世紀80年代初,Reeves首次將粒子系統引入計算機圖形學的實際應用,在電影《星際迷航II:可汗怒吼》(Star Trek II: The Wrath of Khan, Paramount Pictures 1982)中成功模擬火牆效果。

對於追求分辨率和幀率的玩家而言,湍流火焰的高度無序和粘稠焦油的非牛頓流體特性使得二者較難基於物理實時模擬。2002年斯坦福大學的Nguyen等人提出基於物理的火焰模擬方式,使用當時較為先進的奔騰IV處理器,模擬圖1.3右側的火焰效果,每幀的模擬成本也需要3分鐘左右的時間。考慮到如今算力的飛躍,也許小規模的物理火焰能夠做到實時模擬,但隨著三維模擬分辨率的增加,計算複雜度至少以O(n3)的速度增加。與之相比,Lamorlette和Foster為電影《怪物史萊克》(Shrek, DreamWorks SKG 2001)設計出一種以曲線為骨架的非物理火焰模擬方式,實現圖1.4左側的效果只需使用奔騰III處理器每幀渲染2.7秒。


以下采用非物理方式模擬火焰,使用正態分佈函數當作火焰基底,疊加柏林噪聲表示湍流火焰的隨機脈動。Mandelbrot創立分形理論並應用於模擬雪花山脈河流等自然景觀,Gouldin將其引入湍流火焰面的幾何形狀描述並建立了一個預測湍流火焰速度的模型。Daubechies D4小波具有分形特徵,可通過小波變換來實現火焰的分型結構的模擬。而焦油麵需要更平滑的效果,通過改變方差使基底扁平化,再使用Vaidyanathan小波重構。
2 柏林噪聲
2.1 基本思想
現實世界在視覺上是複雜的。如何在計算機圖形學中實現真實感,就是如何從合成的圖像中再現這種複雜性。自然的視覺複雜性(Naturalistic Visual Complexity)由非線性函數的組合中產生,而不是傳統的紋理映射或生長模型算法。基於以上思想,柏林(Ken Perlin)在1982年為《電子世界爭霸戰》(Tron, Disney 1982)工作期間,為生成自然的紋理效果開發出新的噪聲算法,並於1985年正式發表,即柏林噪聲。柏林認為一個好的隨機函數應當具有以下特徵:
1) 旋轉下的統計不變性。無論怎樣轉動它的域,它都具有相同的統計特徵。
2) 頻譜上的窄帶通限制。它在一定狹窄的尺寸範圍內沒有過大或過小的可見特徵。
3) 變換下的統計不變性。無論對域進行怎樣的變換,它都具有相同的統計特徵。
對於柏林噪聲,它還具有噪聲數值連續、沒有間斷點的特點。1989年Perlin與他的學生Hoffert使用基於柏林噪聲的Hypertexture來模擬火球。柏林噪聲也是如今遊戲內生成地形、模擬火焰、雲霧、水面等的方式之一。柏林本人也因為柏林噪聲算法的貢獻獲得了1996年美國電影藝術與科學學院的奧斯卡科學技術獎。

2.2 具體算法
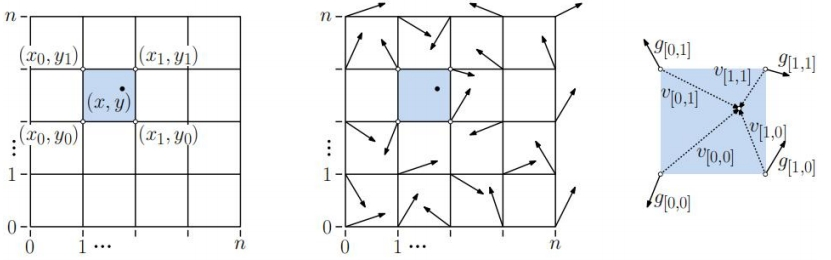
以二維柏林噪聲為例。在空間平面內劃分網格,賦予每個網格頂點一個隨機的方向向量g[i,j],作為該點的梯度值。任取空間平面內一點(x,y),該點的噪聲值,即為該點到四個頂點的距離向量v[i,j],分別與四個頂點的梯度向量做點積的結果。其中距離向量為
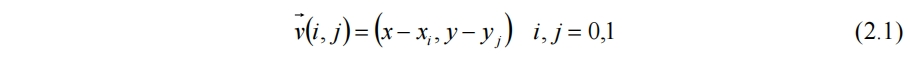
當(x,y)在網格內連續移動時,點積的值將平滑變化,因此噪聲值也會平滑變化。
僅有距離向量並不夠,還需進行加權:
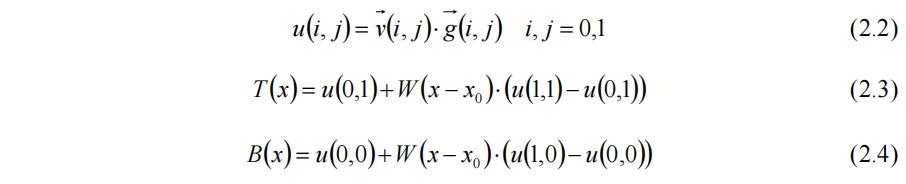
其中W為權函數。二維柏林噪聲的加權結果為
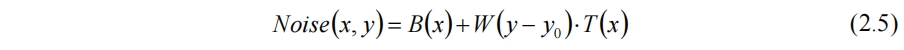
權函數多取
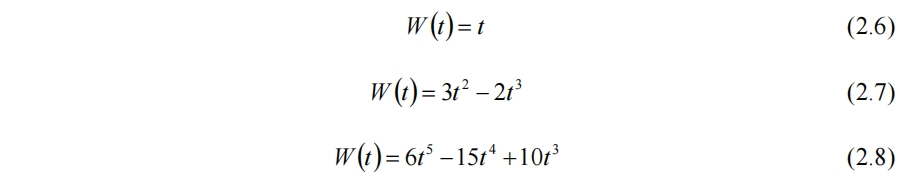
分別對應線性插值和光滑插值,又稱緩和曲線(Ease Curve)。對於頂點的梯度向量,有的約束其長度為1,此處採用單位圓約束,即一個頂點的梯度向量應當位於所在網格的單位圓內。部分柏林噪聲的實現為增強隨機性還需指標隨機化取模查哈希表,還有改進版Simplex噪聲和分形柏林噪聲等,此處不考慮。
2.3 實現效果
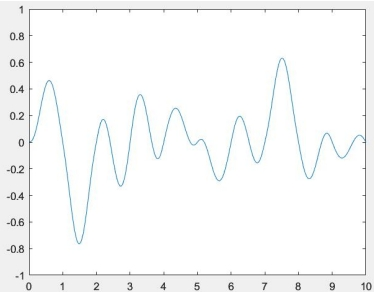
2.3.1 1維靜態柏林噪聲
基於2.2節二維的算法,一維就是一條直線,不考慮單位圓約束條件,結果如圖
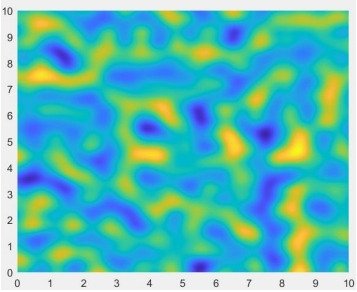
2.3.2 2維靜態柏林噪聲
二維實現方式與2.2節算法相同,採用單位圓約束。結果如圖
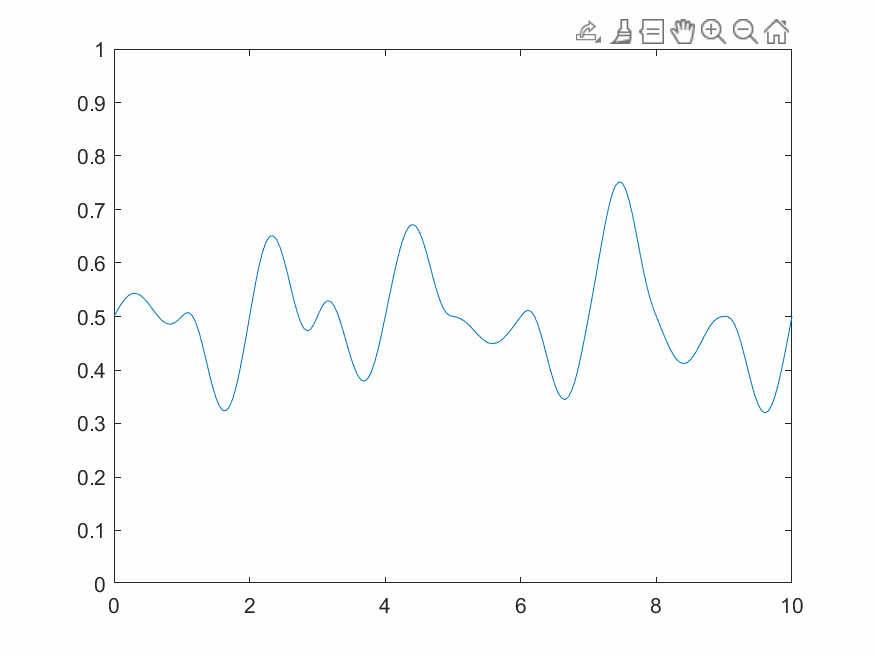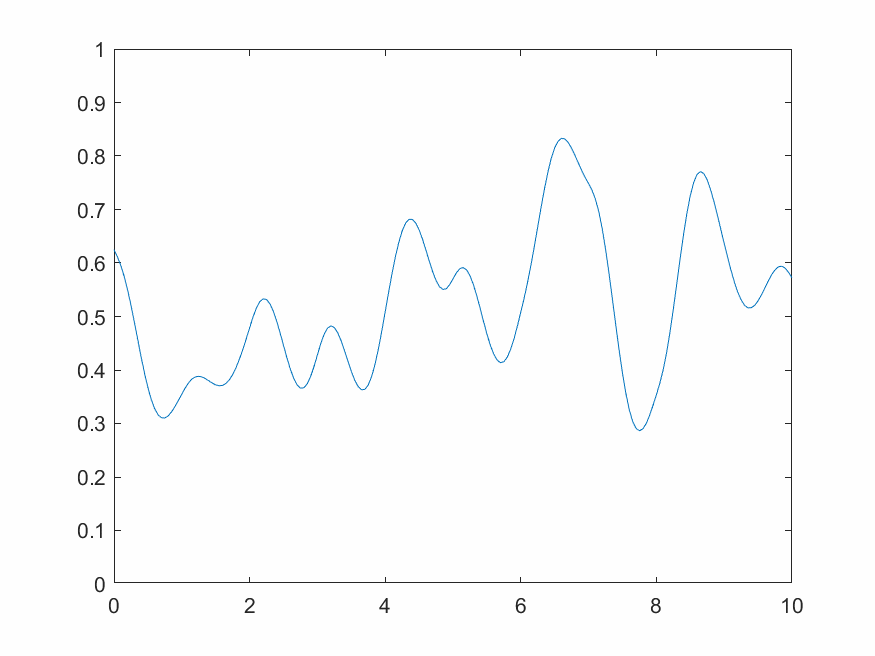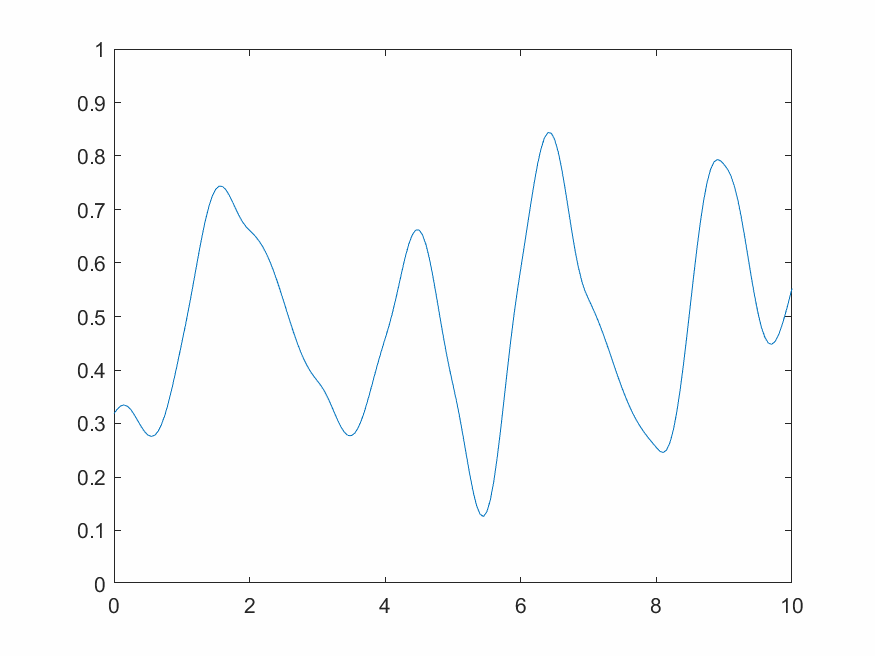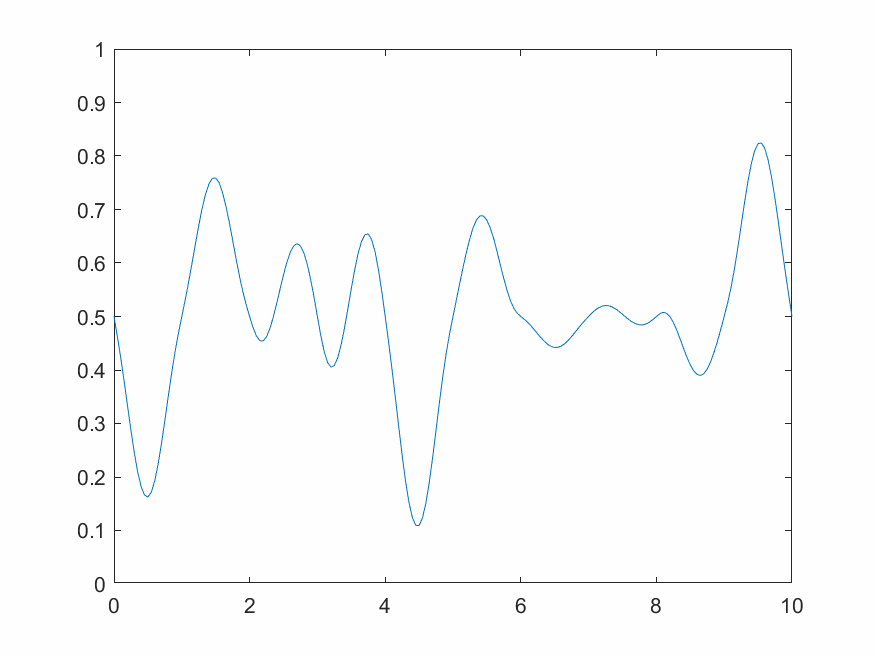
2.3.3 1維動態柏林噪聲
一維動態柏林噪聲是一系列一維柏林噪聲沿時間方向推進演化的結果,需要額外增加一個時間變量並循環不斷輸出。
3 小波變換
3.1 基本思想
3.1.1 何為變換:Sam Porter Bridges
在死亡擱淺送快遞的路上,動力裝甲電量即將耗盡。恰好注意到前方高地處有一個充電樁,而山姆身上帶著兩把摺疊梯。

此時大多數玩家的做法會是:向前方高地搭一個梯子,爬上高地到無線充電樁範圍內充電,再搭一個梯子繼續前進(也可以從原梯子處原路返回)。
變換就是Bridges。因為要充電,所以需要到高地,但又不能瞬移,所以需要經過梯子過去。梯子就是變換,充電就是對經過變換的東西的操作/處理,而再次經過梯子前進或返回就是逆變換。
3.1.2 傅里葉變換和短時傅里葉變換
變換的目的是用一組確定的簡單函數來表示複雜函數f(t),其中確定的簡單函數就是基函數φn。對於正交基有
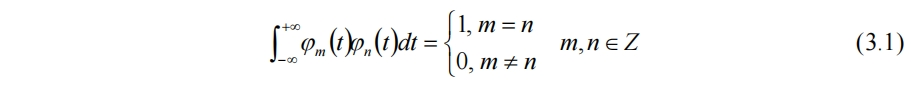
此時f(t)可表示為
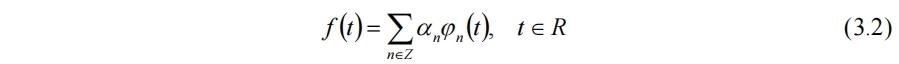
係數為
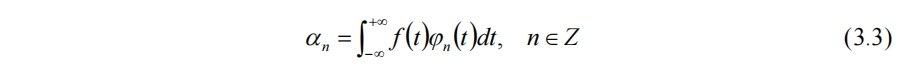
因此f(t)就可以唯一用αn來表示。週期函數進行傅里葉展開時選取的基函數為三角函數,對於非週期函數可視為週期T→∞,有傅里葉變換
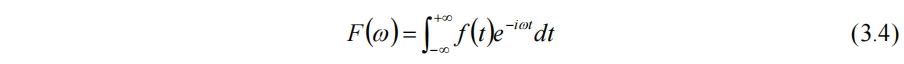
經過傅里葉變換,時域的信號被變換至頻域,能看到該信號中各種頻率分量的含量。但對於非平穩信號,頻率分量會隨時間變化,而傅里葉變換隻顯示該信號含有哪些頻率分量,但並不提供這些頻率在何時出現的信息。這對於分析非平穩信號很不友好。並且用傅里葉變換得到的結果在時間上是全域的,它不能提供信號變化的局部圖像。
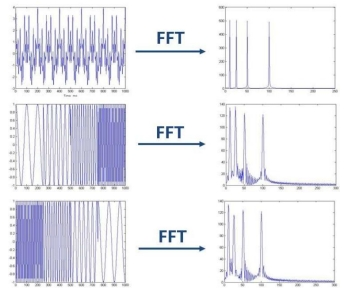
為了克服這一缺點,Dennis Gabor在傅里葉變換中引入窗函數w(t),建立起短時傅里葉變換(STFT,也稱窗口傅里葉變換)。此時使用一個窗函數在一個區間內提取數據,再計算該窗口部分的傅里葉變換。因此STFT可以捕捉到信號中的瞬時響應。
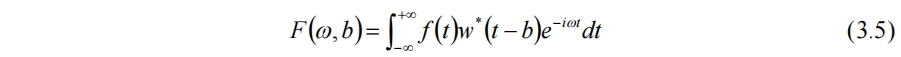
其中w*(t)為w(t)的共軛複數。對於窗函數w(t)還有其他限制,如窗函數在時域和頻域的半寬度滿足海森堡不等式
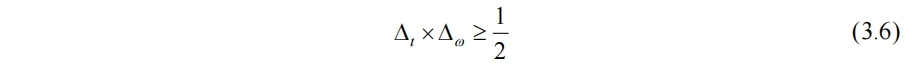
窗函數一旦確定,窗口的大小和形狀就固定不變,其分辨率也隨之確定。如果窗口取的較短,對於波長大於窗口寬度的低頻區域,在頻域的分辨率非常低。如果選一個長窗口,能量在較長的窗口寬度內被平均分配,它在高頻區域時域的分辨率就很差。因此,如果一個信號由短時間的高頻和長時間的低頻組合而成,那麼窗口函數就無法捕捉全該信號的重要信息。從(3.6)也可看出時域分辨率和頻域分辨率的矛盾性。
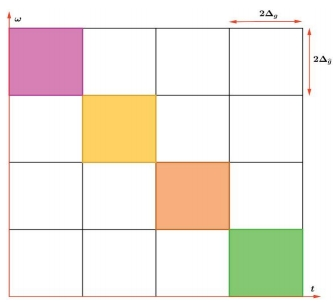
3.1.3 小波變換
為了進一步彌補STFT的缺點,小波函數應運而生。在最簡單的意義上一個小波可以被定義為一個衰減速度快且平均值為零的波函數。
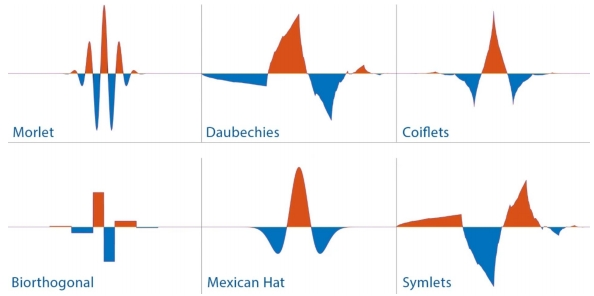
小波變換表示局部的時間和頻率信號,它比傅里葉模式更能有效地檢測間斷點。它的形狀可以改變,在捕捉較低頻率時變寬,而在捕捉高頻時變窄。
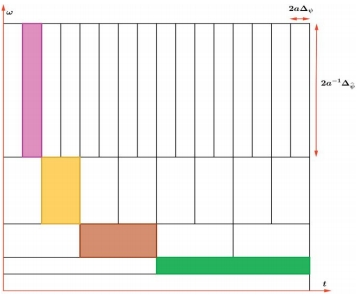
小波變換仍沿用STFT中的瞬態窗口,但隨著頻率的增加的同時,增加時間分辨率,即令帶寬與頻率成正比。選定一個小波函數ψ稱為母小波,通過對其伸縮和平移可生成一系列小波:
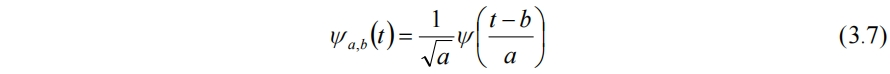
與窗函數對比,可見小波函數除了平移參數b,還有另一個可調的尺度參數a,因此能夠實現窗口的改變。而連續小波變換為
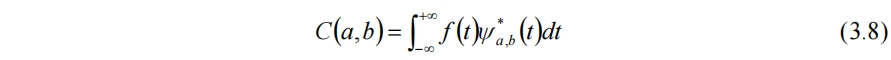
連續小波變換存在一些缺點,如冗餘和不實用的問題。而離散小波變換解決了連續小波變換的不足。常用方式為將(3.7)中的a和b分別取
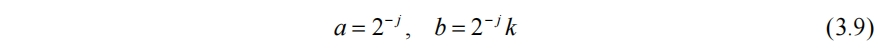
此時小波離散為
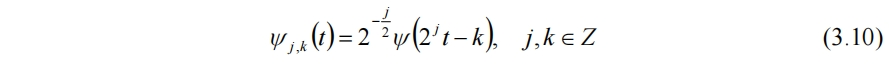
對應的離散小波變換為
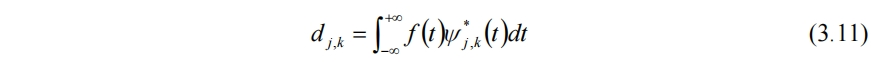
其中dj,k是小波係數。若小波系列能構成L2(R)空間的正交基,f(t)可重構為

許多經過小波變換的函數在轉換到小波域時顯得稀疏,很多係數都在0附近,因此小波變換常被用於數據去噪、圖像壓縮等領域。小波還有很多其他數學基礎涉及到泛函分析、群論等,非所學專業不再展開。
3.2 尺度函數、小波函數和多分辨分析
以Haar小波為例引入小波變換中重要的基礎概念:尺度函數和小波函數,介紹離散信號的多分辨表示。
3.2.1 尺度函數
對於信號x={x1,x2},定義其平均與細節分別為
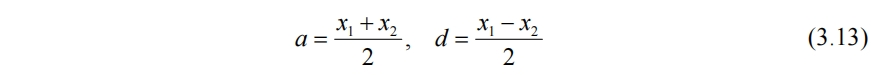
使用平均a與細節d重構信號,有
因此a和d是原信號x={x1,x2}的一種表示方式。
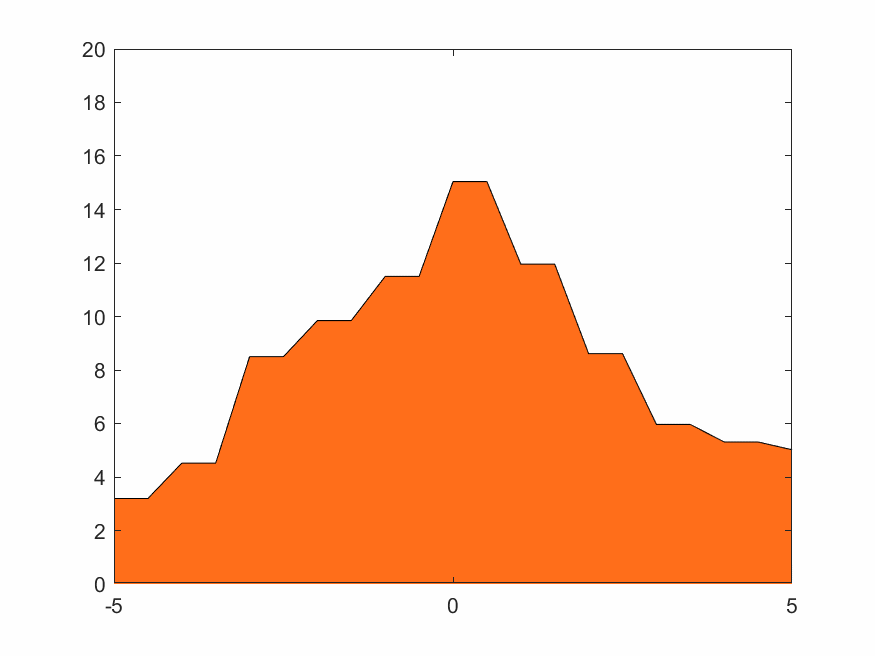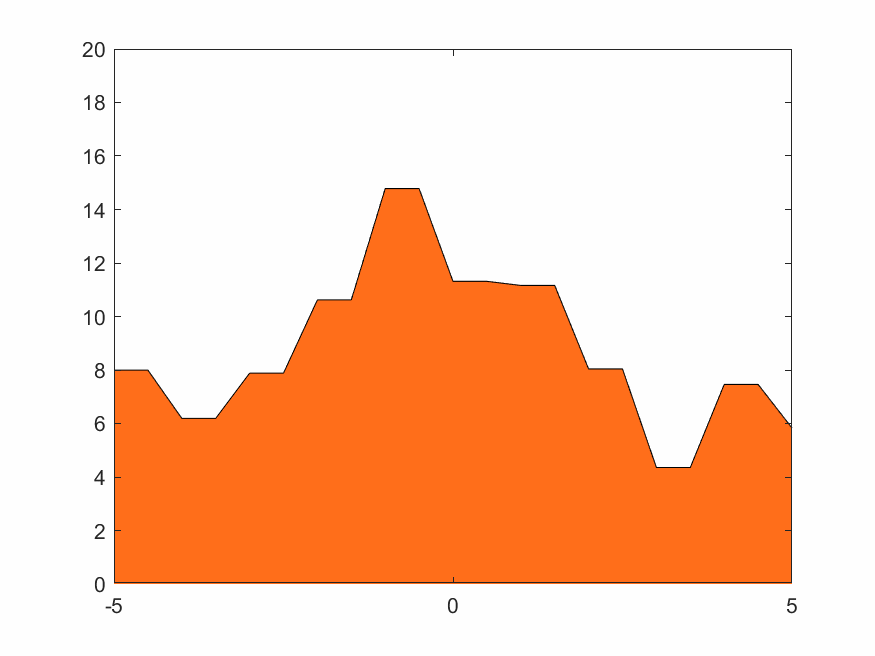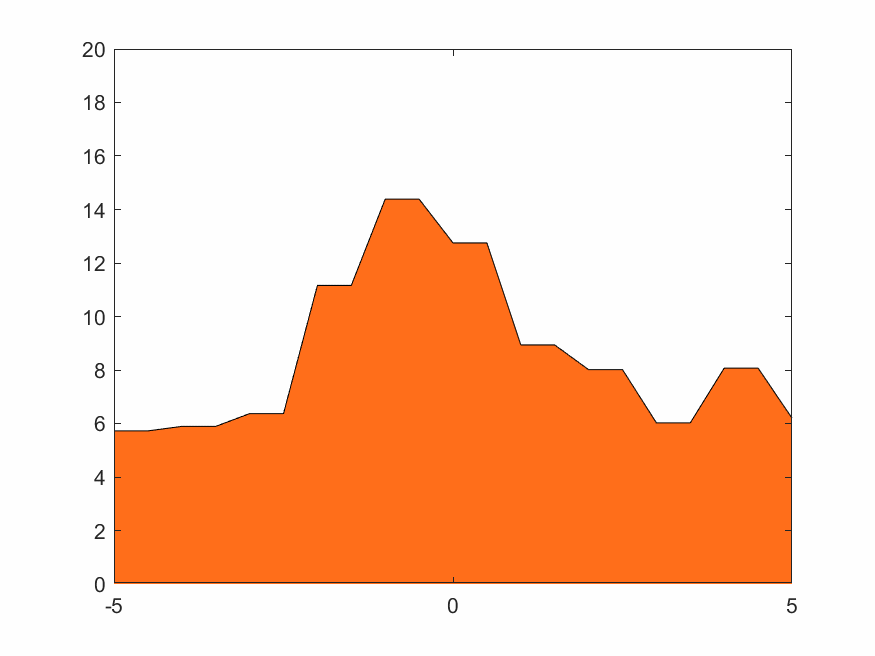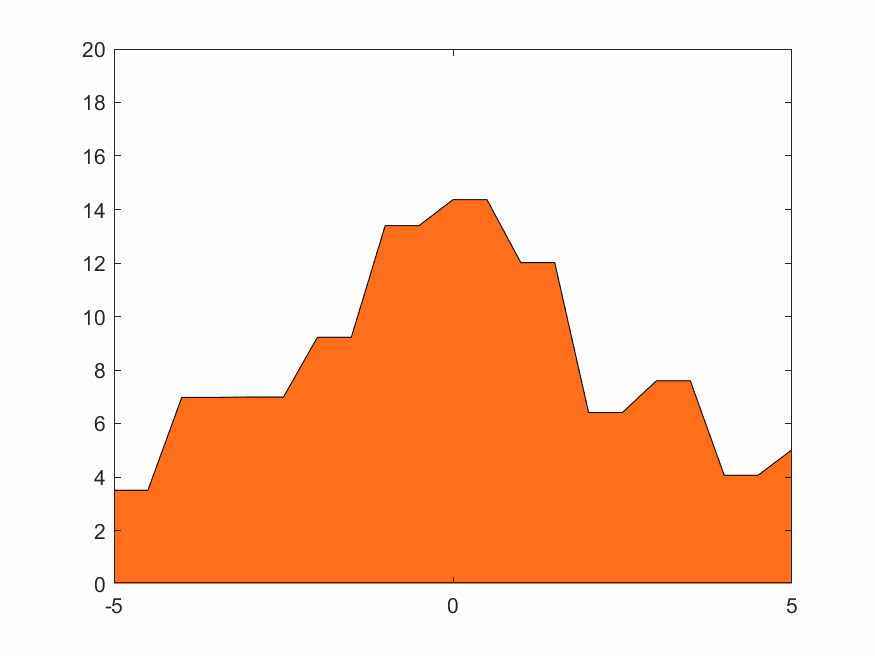
考慮分段離散信號f(t)如圖,
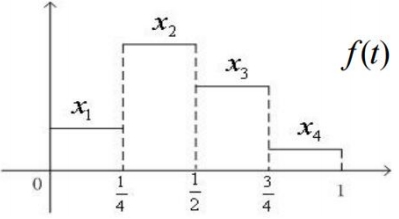
第一次取平均和細節
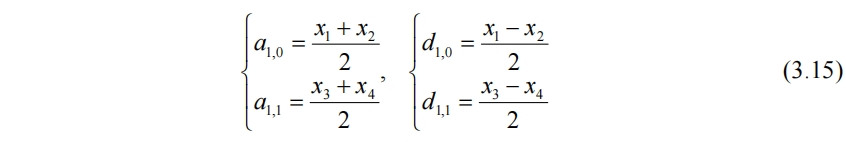
對於a1,0和a1,1還能再取一次平均和細節
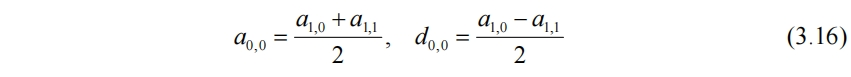
同樣,原信號也可以由a0,0、d0,0、d1,0和d1,1重構回來。
對於圖3.7的信號,考慮使用最簡單的常數函數來擬合。定義尺度函數
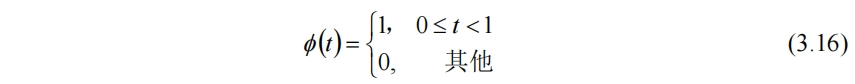
圖像如3.8所示
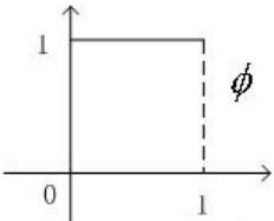
若要擬合f(t),需要尺度函數的區間更短,如果Φ(t)只在[0,1/4)上那麼f(t)的第一段就可以表示為f1(t)=x1Φ(t),t∈[0,1/4),第二段可視為Φ(t)在[0,1/4)上向右平移1/4個單位再與x2相乘。因此對尺度函數Φ(t)進行伸縮和平移變換(非標準化),有
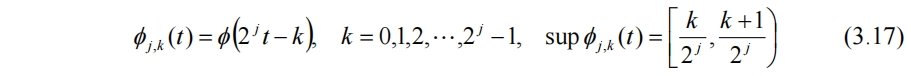
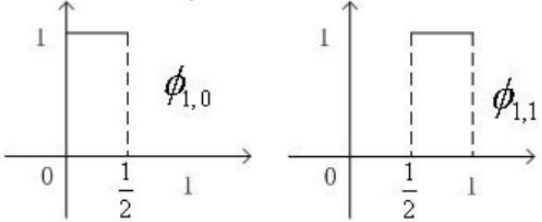
為描述f(t)需要Φ(t)伸縮2次、平移3次,此時
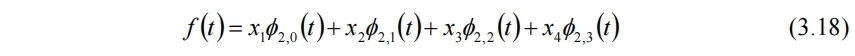
現在能夠使用經過伸縮和平移的尺度函數描述原信號f(t),但還需原信號本身的信息x1~x4。能否使用平均信息a1,0和a1,1結合尺度函數來表示f(t)?
假設有g(t)滿足要求,
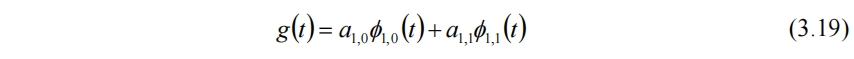
當t=1/8時,f(t)=x1,而g(t)=a1,0=(x1+x2)/2,並不相等。顯然只用平均量a並不能重構回原信號,還需要引入細節量d。
3.2.2 小波函數
比較g和f的差別,可以發現g需要在[0,1/4)內加上x1/2同時減去x2/2,在[1/4,1/2)上相反,減去x1/2同時加上x2/2。而這加減的恰好是(3.15)式中的細節d1,0,只是在相鄰兩個區間內正負號相反。引入Haar小波函數ψ(t)
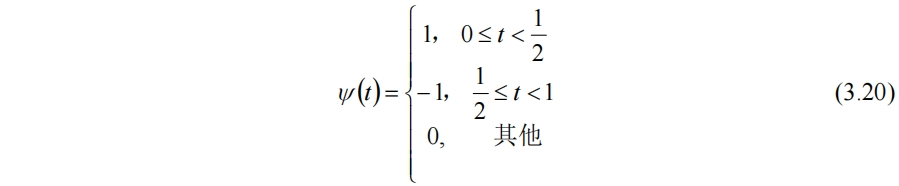
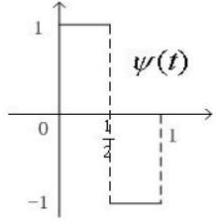
ψ(t)同樣可以進行伸縮和平移(非標準化),
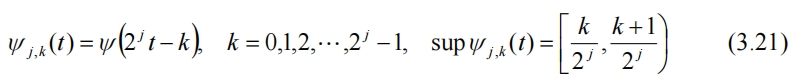
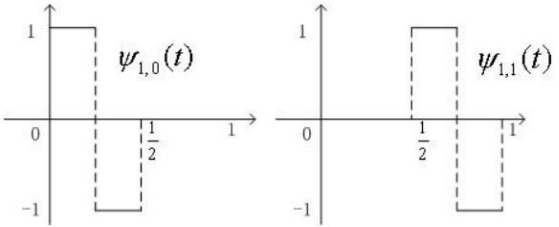
此時,f(t)就可使用平均量a和細節d,以及尺度函數和小波函數完整重構
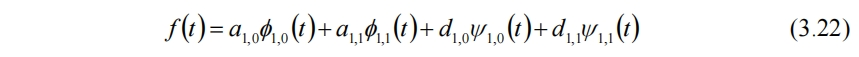
3.2.3 多分辨分析
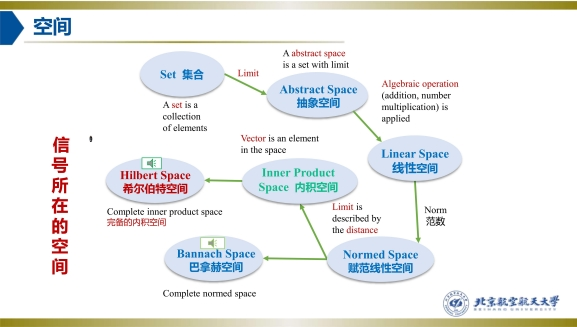
多分辨分析(Multiresolution Analysis)從函數空間特別是線性代數中內積空間、正交和、正交補、基等的角度出發進行分析。在尺度函數(3.17)和小波函數(3.21)伸縮平移的過程中,j每增加1函數就縮短為原來的一半,每次平移的分辨率就越高。而同一個信號,又可以用不同層級分辨率的尺度函數和小波函數來表示。如(3.22)使用第一層的平均和細節重構f(t),也可以使用第二層的平均和細節與第一層的細節共同重構:
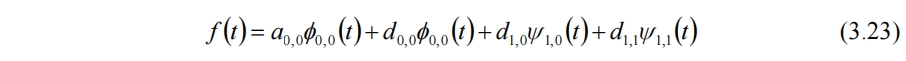
如果信號更長,還可以繼續分解下去。
不同尺度之間通過兩尺度方程聯繫。顯然尺度函數和小波函數滿足
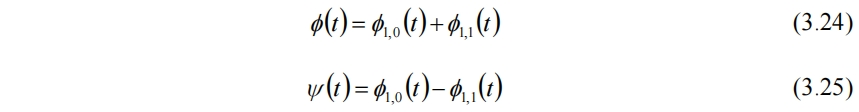
對於其他尺度同理。真正嚴謹的多分辨分析,還需參考教材深入學習。

4 2維火焰面和焦油麵模擬
4.1 火焰面模擬
最基礎的火焰形狀在很多遊戲中都出現過,如各種中世紀遊戲中必不可少的火把,以及在黑暗靈魂3(Dark Soul III, FromSoftware 2016)中常見的篝火火焰,可見基本形狀與正態分佈類似。
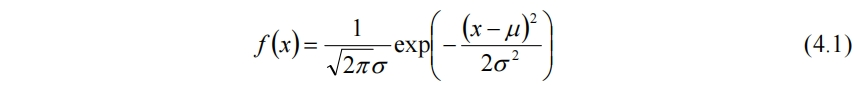
因此選擇以正態分佈函數為基底,線性疊加噪聲來模擬湍流火焰的無序動態燃燒效果。參數a和b用於調控形狀
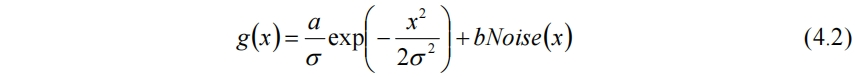
湍流火焰鋒面應當尖銳、粗糙而非光滑,可以考慮用柏林函數在低分辨率下線性插值,不做小波變換。火焰具有分形特徵,也可以考慮對光滑表面做Daubechies D4小波變換構造分形火焰面。對於蒸汽朋克世界,如果處處都是齒輪,連火焰面都是鋸齒也未嘗不可,此時可以使用Haar小波變換。結合麥克斯韋的彈性齒輪、惰輪電磁場模型,可以從底層的齒輪架構電磁場開始構造純正的齒輪蒸汽朋克世界。
4.1.1 小波變換效果
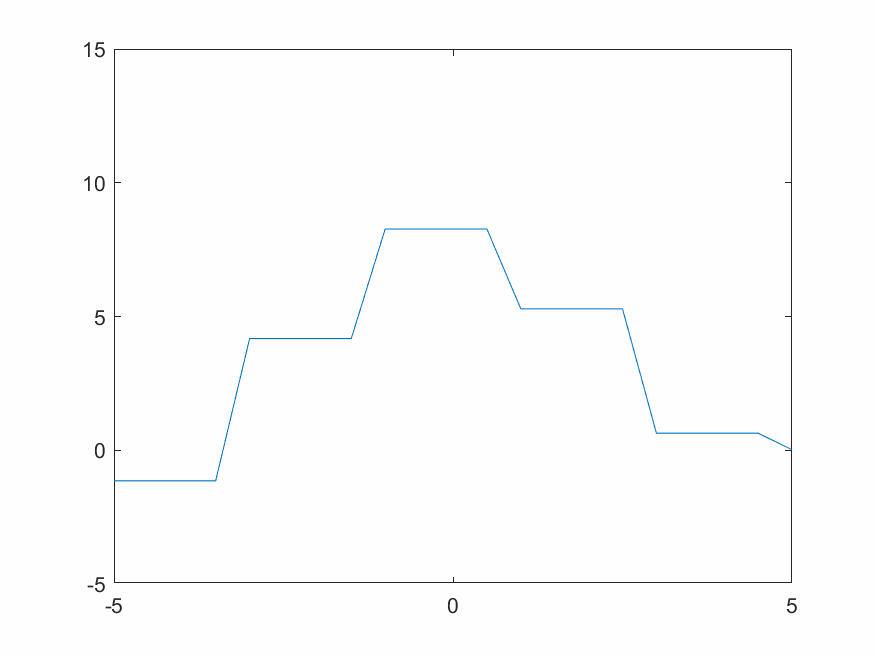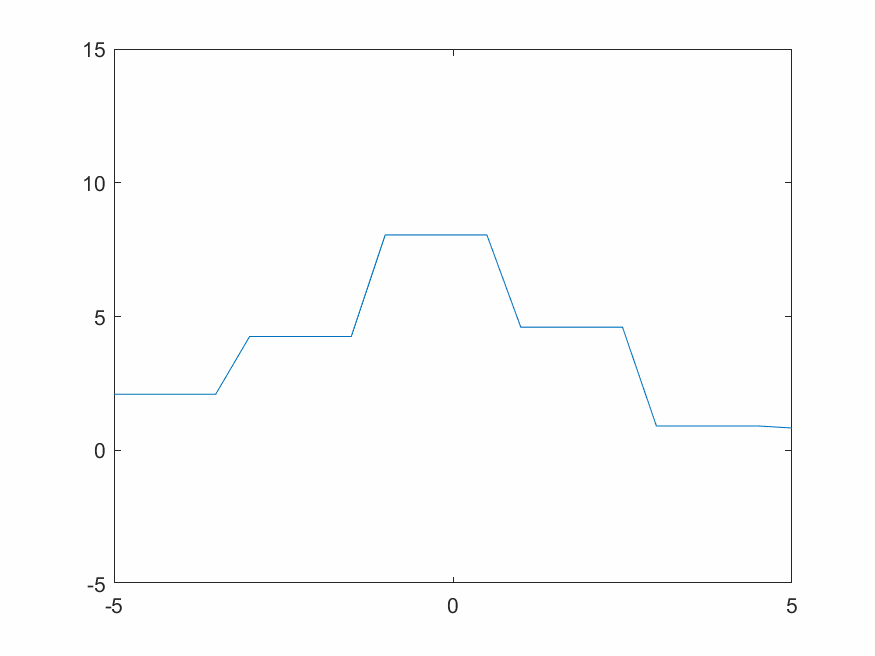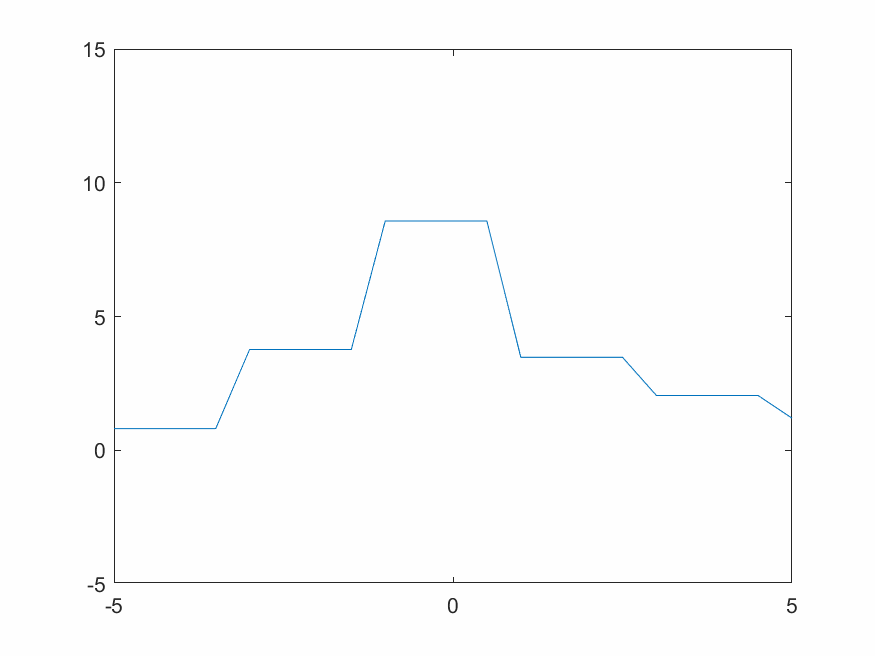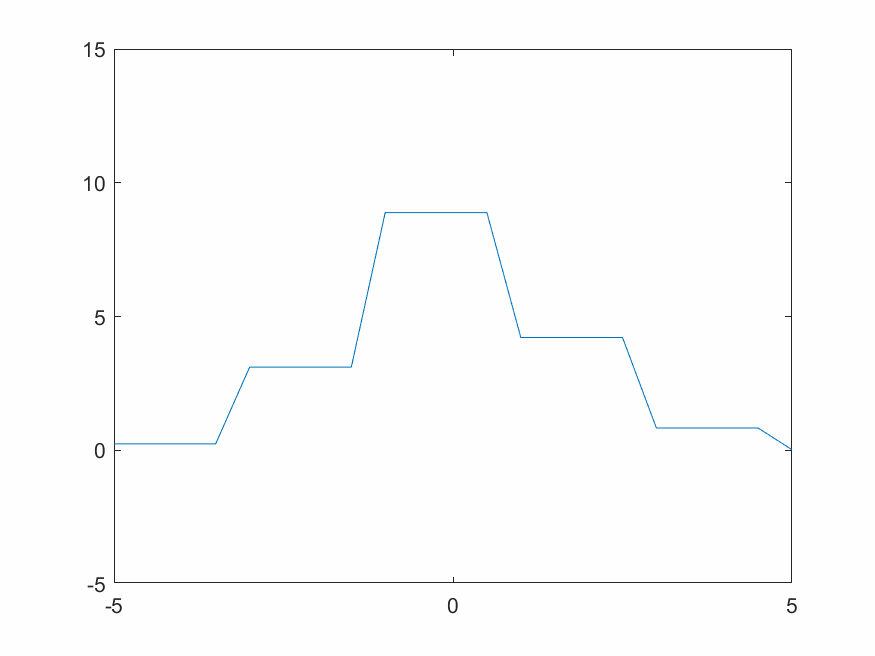
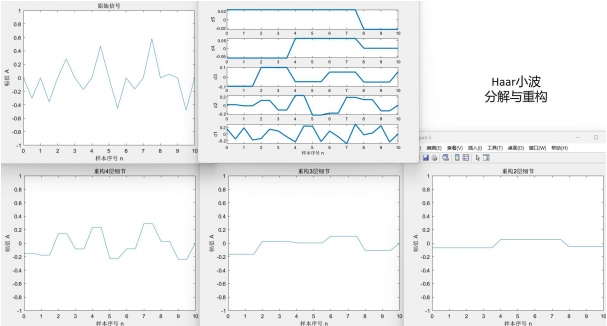
對於一個固定的柏林噪聲波形,選擇不同小波進行變換有不同效果。xy分辨率較低時去掉細節會使整體波形更平緩。用同樣的細節層數重構,光滑小波比不光滑的小波重構出來的結果顯然更光滑。圖4.2~4.4的xy分辨率為0.5,使用線性插值。
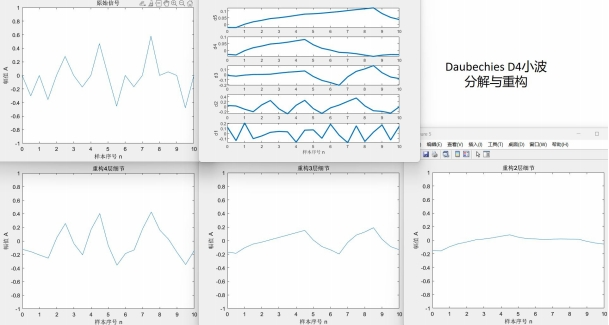
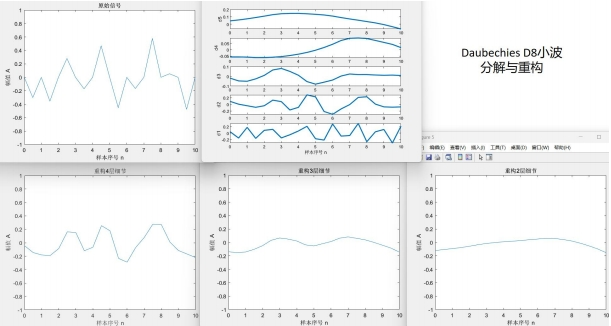
D8小波比D4小波更光滑,從下方三張重構結果圖片也可看出D8重構結果比D4更光滑。Haar小波本身就是鋸齒形,重構出來的波形也一定有鋸齒特色。這也是適合蒸汽朋克的原因。
而在高分辨率下,結合多項式插值,波形本身比較光滑。用不光滑的小波重構,其去掉細節的平均量會使波形變粗糙,向所使用的小波函數靠攏。圖4.5~4.6的xy分辨率為0.05,可見去掉越多的細節,D4小波變換後的結果越粗糙。而本身光滑的Vaidyanathan小波效果相反。
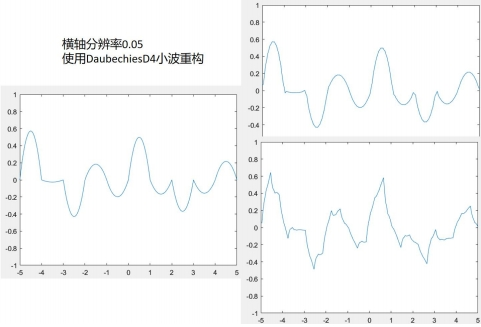
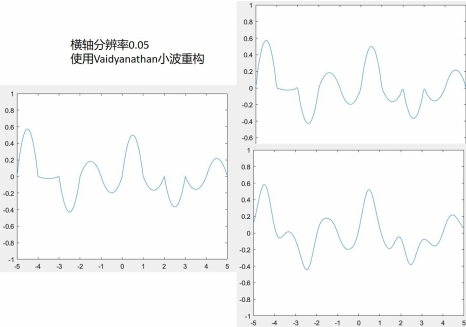
因此對於火焰模擬有以下方式,一是低分辨率不進行小波變換,也可以進行Haar小波變換,另一種是高分辨率進行D4小波變換。
4.1.2 低分辨率無變換火焰
在(2.3)~(2.5)式中的權函數取線性插值,即(2.6)式。結果如下
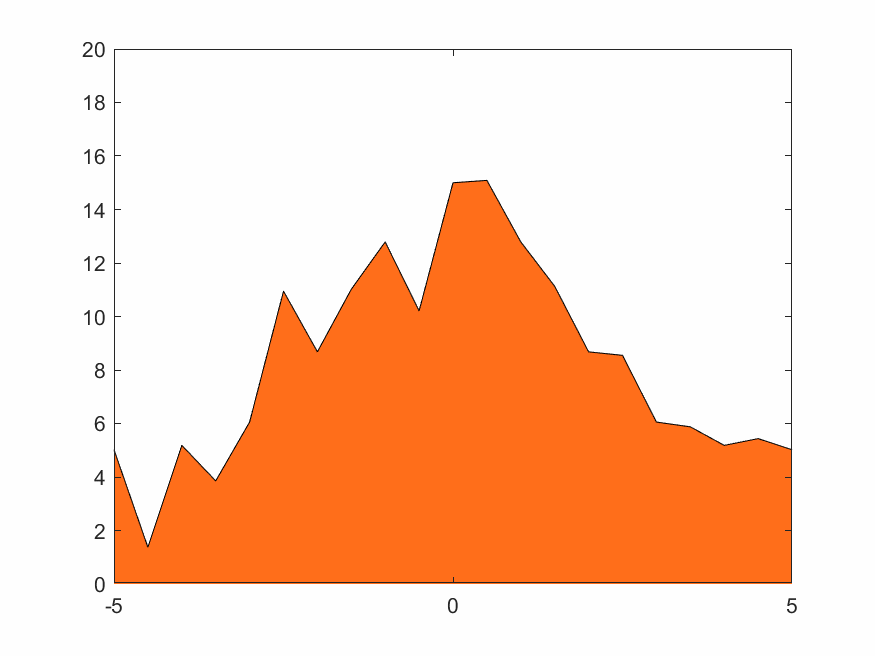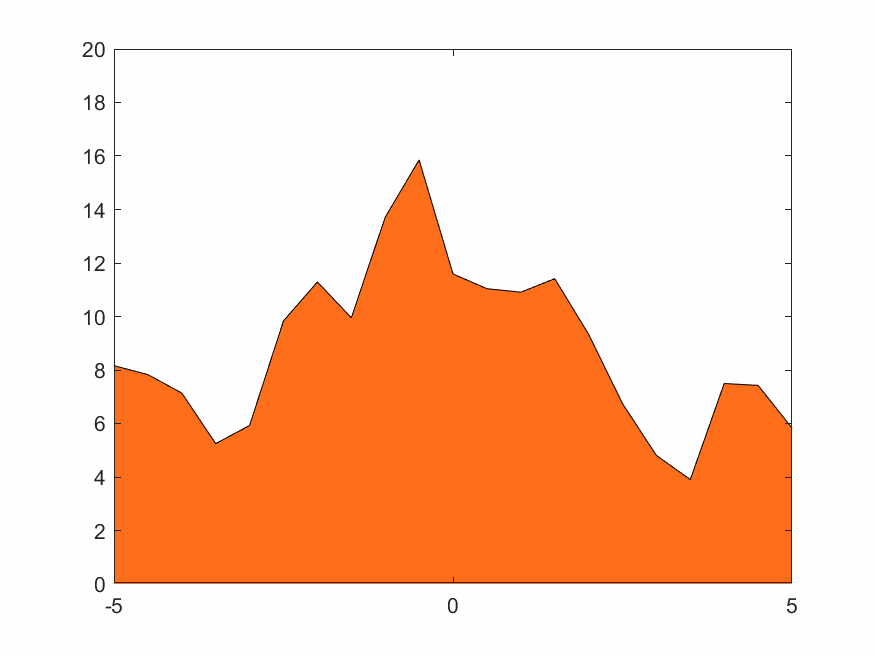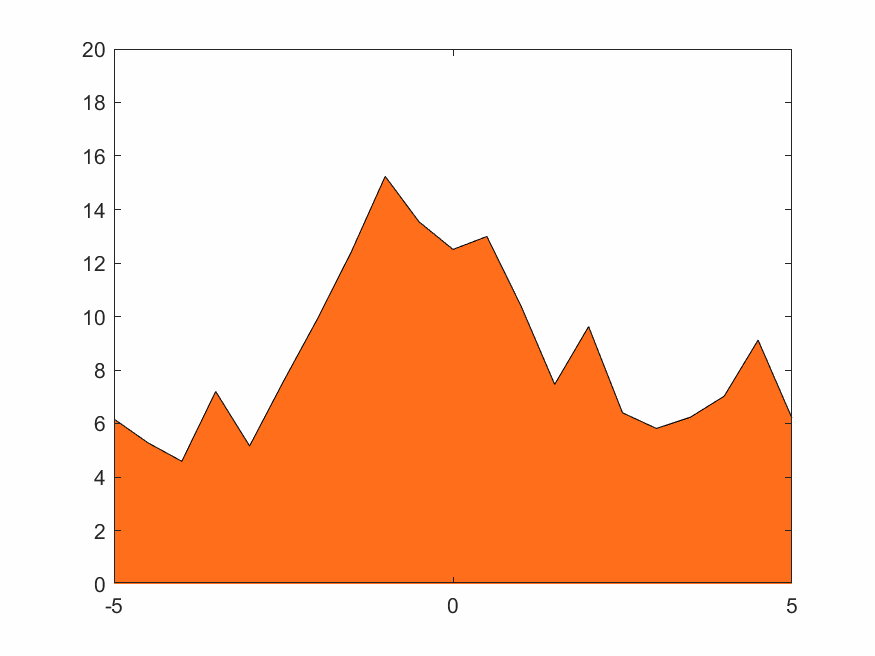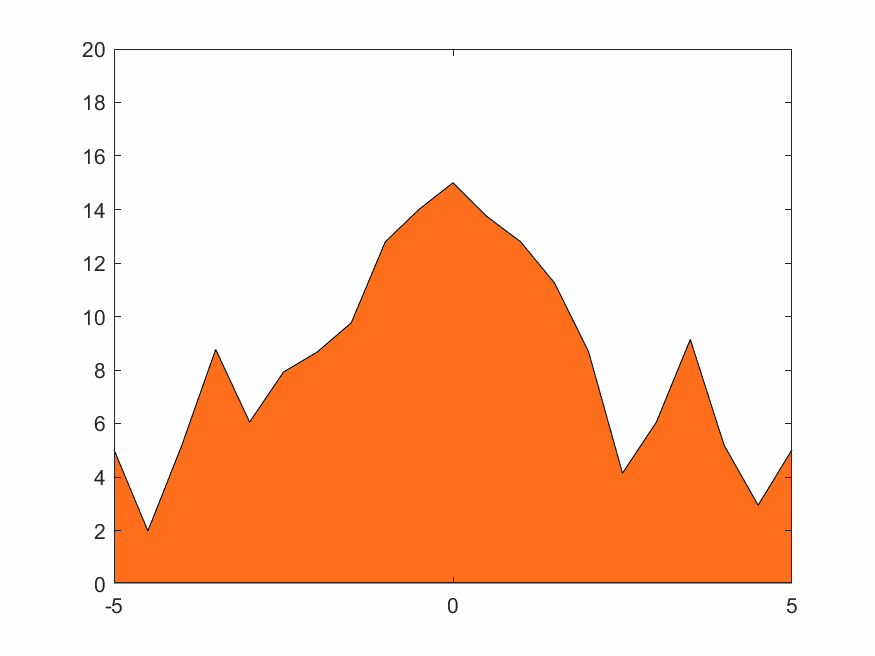
4.1.3 低分辨率Haar小波變換
Haar的移動城堡、蒸汽朋克下的鋸齒火焰,效果如下
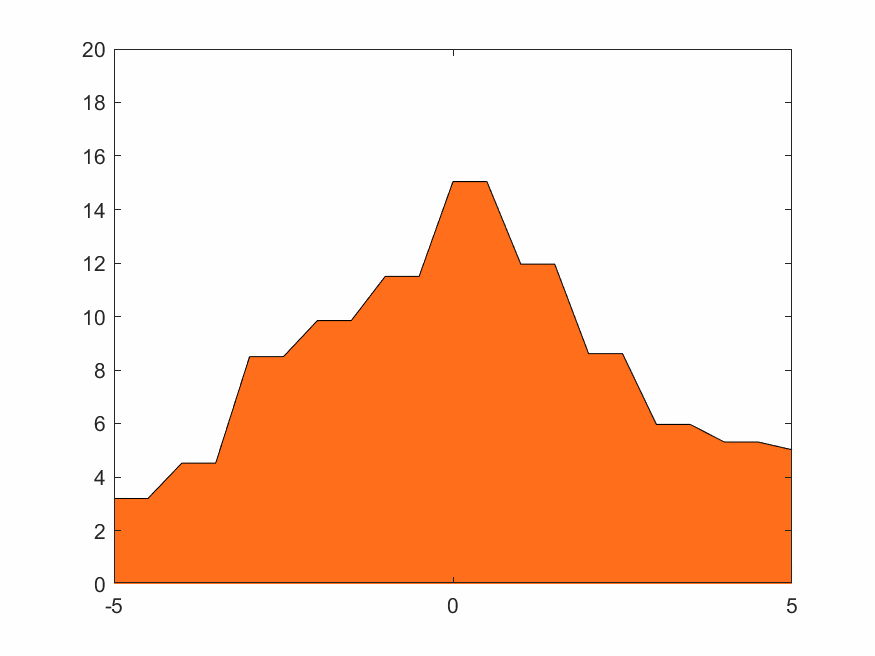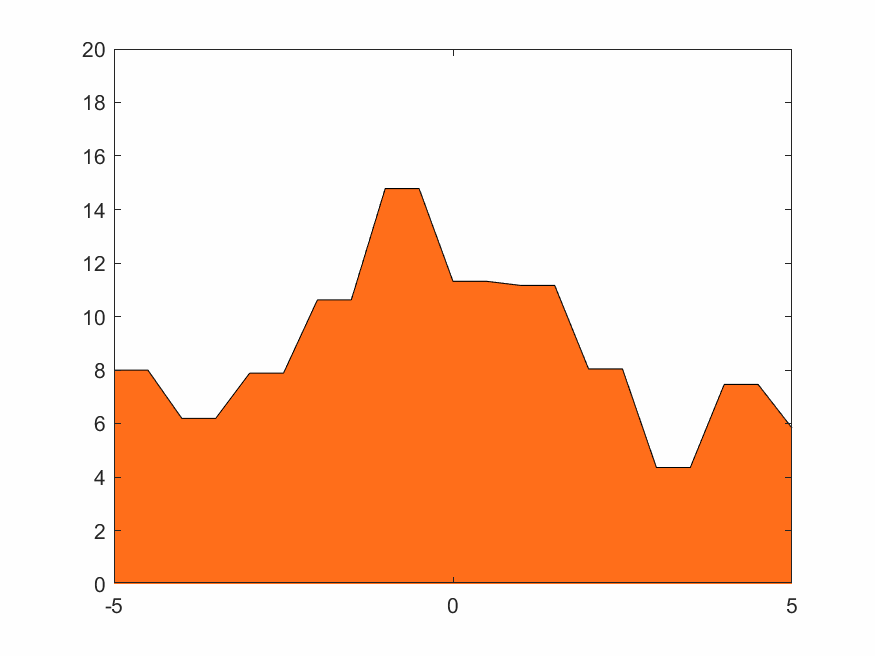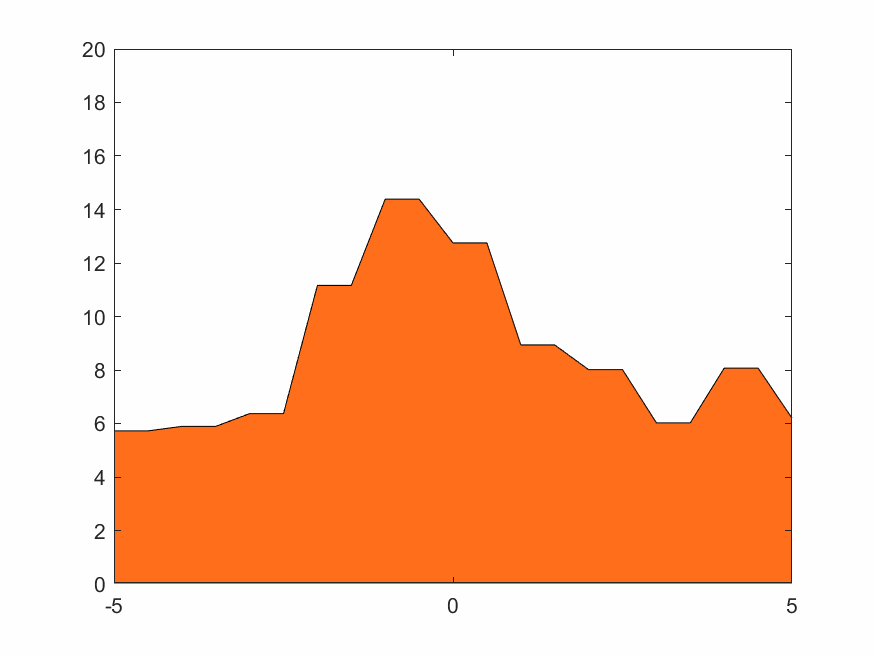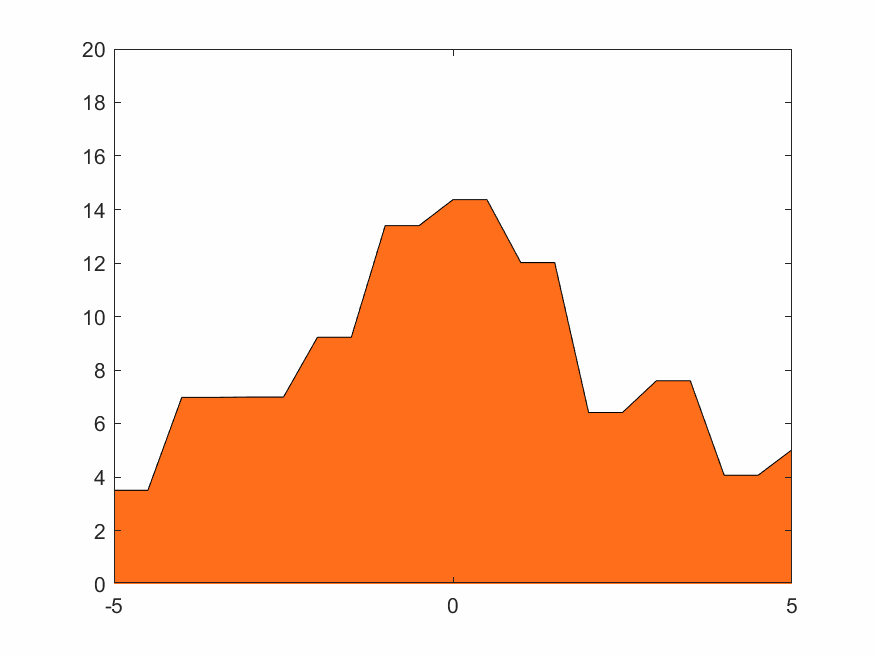
4.1.4 高分辨率D4小波變換
xy分辨率為0.05,權函數用(2.7)式,通過Daubechies D4小波變換去掉3層細節:
可見重構後的火焰也具有了分形的特點。但這樣非物理的簡單模擬出的火焰看上去還是不夠自然。
由於正態分佈函數在遠離軸的位置函數值很小,而柏林噪聲函數在整個範圍內均值不變,因此火焰圖像有比較明顯的上下波動。可通過對柏林噪聲項加入阻尼函數來解決這一問題。
4.2 焦油麵模擬
正態分佈函數的標準差σ可以控制其圖像的分散程度,如果σ較大則圖像扁平,適合模擬有表面張力效果的水面。此時柏林噪聲為水面上的波動如起泡等。少量的冒泡需要限制柏林函數在區域兩端的值,因此(4.2)式改為
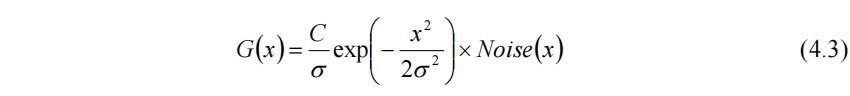
這樣的水面模擬和火焰面模擬具有同樣的問題,與上篇文章所述的淺水方程類似,自由表面都使用了表面函數假設的限制,同一個x位置不能出現兩個函數值,因此無法模擬真正的起泡脫離表面、海浪捲起等效果。還可以將焦油麵和火焰面結合,實現燃燒的焦油麵效果,因為二者完全可以共用一套隨機數。

對不起,做不到
記
關於物理真實和視覺真實的討論,可參考上篇水體模擬中的“記”,Fournier和Reeves有相當精彩的論述。此外Ebert等仍強調,"For entertainment applications, empirical accuracy is not the goal; visual verisimilitude is, and visual novelty might prove even more useful."
對於火焰模擬和水體模擬的區別,Lamorlette和Foster指出:"Fire on the other hand, is a dramatic element that requires the maximum level of control possible while maintaining a believable appearance. We expect fire to look complex and unpredictable, while at the same time having a recognizable structure according to the conditions under which it is burning. That complexity by itself makes direct numerical simulation of fire much less attractive than for other phenomena..."令人信服的火焰外形應當是不可預料的,但火焰動畫又必須可控,按照藝術創作者的需要綻放。所以它不能是純物理的,這樣對創作者而言就缺少調整方式;它也不能是純動畫的,這樣太不真實。本篇實現的分形火焰雖然看著像個火焰,但很缺乏真實性。也許基於上述內容可以加入一些物理的模擬構造出更逼真的效果。而焦油模擬的效果顯然比火焰要好,實際上這兩個效果都是基於完全相同的隨機數種子生成的(取消了隨機數生成器,改為輸入一組固定數據)。這也是Lamorlette等看法的又一印證。
實際上在D4火焰效果實現後發現,早在2009年工業光魔公(Industrial Light & Magic)的兩位研究員Horvath和Geiger就已經將小波變換引入計算機圖形學的火焰模擬過程:We augment the PIC/FLIP technique by using a simple wavelet decomposition on the velocity grid to produce multiple levels of detail. This allows us to amplify vorticity at multiple scales as well as accelerating convergence of the iterative incompressibility solution.他們的思路也是使用小波分解來增強火焰的細節,但包含物理求解不可壓NS方程的過程,也有一套具體實現方案。他們使用NVidiaQuadro5600 GPU,每個切片的每一幀平均需要20秒來模擬。使用10個GPU,模擬通常需要2到4個小時,渲染需要另外的1到2個小時。實現結果如圖。
同樣使用了小波變換,但不得不說Horvath和Geiger的實現結果與按本篇方案的效果相比簡直沒法比。

遊戲創作就是藝術創作。不僅如此,更底層的計算機圖形學也是藝術。Musgrave、Peachey和Ebert等對梵高、修拉的繪畫作品與計算機圖形學進行對比:"Good painters evoke worlds of color in a painting, and even in a single brush stroke. Van Gogh, who painted with a palette knife, not a brush, executed several paintings in the morning, took a long lunch, then did several more in the afternoon. Painting in a hurry, he didn't mix his paints thoroughly before applying a thick blob to the canvas. Thus each stroke has a universe of swirling color within it. Seurat's pointillism is another form of what painters call juxtaposition, or the use of a lot of different colors to average to some other color. This is part of the visual complexity that, to me, distinguishes good paintings from most computer graphics."
確實,好的畫家用一幅畫,甚至一筆就能向觀眾喚起一個色彩的世界。如今AI取得了前所未有的飛躍,但距離真正的人、創作的人、理性的人、遊戲的人,還差得遠。

參考文獻
[1] Ten Lectures on Wavelets, Ingrid Daubechies
[2] 《小波變換》課件,BUAA王海輝教授
[3] An Image Synthesizer, K. Perlin
[4] Hypertexture, K. Perlin, M. Hoffert
[5] Depicting Fire and Other Gaseous Phenomena Using Diffusion Processes, J. Stam et. al.
[6] Interactive Simulation of Fire, Z. Melek et. al.
[7] Particle Systems-Technique for Modeling a Class of Fuzzy Objects, Reeves, William T.
[8] A Technique for Art Direction of Physically Based Fire Simulation, A. Bangalore et. al.
[9] Physically Based Modeling and Animation of Fire, Nguyen et. al.
[10] Breeding Terrains with Genetic Terrain Programming: The Evolution of Terrain Generators, Frade et. al.
[11] A Fire Flame Simulation Scheme with Massively Parallel Processing, Byeong-uk Im et. al.
[12] The Fractal Geometry of Nature, Mandelbrot
[13] Directable, High-Resolution Simulation of Fire on the GPU, Horvath et. al.
[14] Laminar Flamelet Concepts in Turbulent Combustion, N. Peters
[15] Improving Noise, K. Perlin
[16] Generating and Rendering Procedural Clouds in Real Time on Programmable 3D Graphics Hardware, Hasan et. al.
[17] Introduction to Wavelet Transforms, Bhatnagar
[18] Generation of Augmented Bathymetry to Aid Development of Terrain-Aided Autonomous Underwater Vehicle Localization and Navigation Approaches, Heubach et. al.
[19] A Parallel Algorithm Using Perlin Noise Superposition Method for Terrain Generation Based on CUDA architecture, Li et. al.
[20] Texturing and Modeling: A Procedural Approach, Ebert et. al.
[21] 小波變換與圖像、圖形處理技術,孫延奎
[22] Wavelet Analysis: Basic Concepts and Applications, Arfaoui et. al.
[23] Wavelet Transforms, Kith and Kin, Shah et. al.
[24] Wavelets and Wavelet Transform Systems and Their Applications: A Digital Signal Processing Approach, Akujuobi
[25] 形象易懂講解算法I——小波變換,https://zhuanlan.zhihu.com/p/22450818
[26] 從傅里葉(Fourier)變換到伽柏(Gabor)變換再到小波(Wavelet)變換,https://blog.csdn.net/jbb0523/article/details/42028587
[27] The Art of Fluid Animation, J. Stam
[28] Structural Modeling of Flames for a Production Environment, Lamorlette et. Al.
[29] Combustion Physics: Flames, Detonations, Explosions, Astrophysical Combustion and Inertial Confinement Fusion, Liberman
[30] Gas Turbine Combustion: Alternative Fuels and Emissions, Arthur Lefebvre
尾
及格再放代碼,不及格就重修
