引
最终幻想7重制版使用“湍流火焰”与“逃离混沌”的前章标题呼应,死亡搁浅的非牛顿流体焦油又如何模拟。Haar小波重构出Haar的移动城堡,肯·柏林拿下奥斯卡技术成就奖,Daubechies太强以至理解不能。最终只是实现这样的效果:分形湍流火焰面
Haar的移动城堡?
或蒸汽朋克风格的锯齿火焰面(结合麦克斯韦弹性齿轮惰轮电磁场模型,从底层原理出发构建“纯齿轮的蒸汽朋克”)
粘性焦油面效果
最终幻想7重制版,是逃离混沌还是踏入混沌的“湍流火焰”?

计算机图形也要与修拉和梵高一决高下
序
What I cannot create, I do not understand.
Richard Feynman
1 概述
在最终幻想7重制版(Final Fantasy VII Remake,SQUARE ENIX 2020)最终决战前、命运的岔路口处,刚刚经历第17章名为“逃离混沌(Deliverance from Chaos)”的主角团们,不得不再次踏入象征混沌的“湍流火焰”,非常巧妙的呼应(当然这里并非真的火焰,只是具有湍流火焰的流动特征)。在死亡搁浅(Death Stranding, Kojima Project 2019)中,焦油作为冥滩出现在现实世界的副产物之一,也属于死亡搁浅世界观下的标志性物质,它的高粘性从游戏中也能略窥一二。

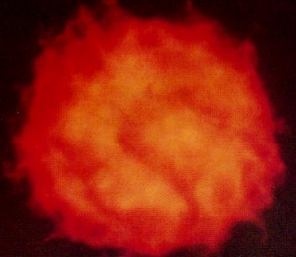
“艺术就是爆炸”,爆炸伴随燃烧。它们都是各种娱乐作品里的常客,也多是作品体验过程中的高峰。与水体模拟类似,火焰模拟在计算机图形学和电子游戏、影视特效制作中必不可少。20世纪80年代初,Reeves首次将粒子系统引入计算机图形学的实际应用,在电影《星际迷航II:可汗怒吼》(Star Trek II: The Wrath of Khan, Paramount Pictures 1982)中成功模拟火墙效果。

对于追求分辨率和帧率的玩家而言,湍流火焰的高度无序和粘稠焦油的非牛顿流体特性使得二者较难基于物理实时模拟。2002年斯坦福大学的Nguyen等人提出基于物理的火焰模拟方式,使用当时较为先进的奔腾IV处理器,模拟图1.3右侧的火焰效果,每帧的模拟成本也需要3分钟左右的时间。考虑到如今算力的飞跃,也许小规模的物理火焰能够做到实时模拟,但随着三维模拟分辨率的增加,计算复杂度至少以O(n3)的速度增加。与之相比,Lamorlette和Foster为电影《怪物史莱克》(Shrek, DreamWorks SKG 2001)设计出一种以曲线为骨架的非物理火焰模拟方式,实现图1.4左侧的效果只需使用奔腾III处理器每帧渲染2.7秒。


以下采用非物理方式模拟火焰,使用正态分布函数当作火焰基底,叠加柏林噪声表示湍流火焰的随机脉动。Mandelbrot创立分形理论并应用于模拟雪花山脉河流等自然景观,Gouldin将其引入湍流火焰面的几何形状描述并建立了一个预测湍流火焰速度的模型。Daubechies D4小波具有分形特征,可通过小波变换来实现火焰的分型结构的模拟。而焦油面需要更平滑的效果,通过改变方差使基底扁平化,再使用Vaidyanathan小波重构。
2 柏林噪声
2.1 基本思想
现实世界在视觉上是复杂的。如何在计算机图形学中实现真实感,就是如何从合成的图像中再现这种复杂性。自然的视觉复杂性(Naturalistic Visual Complexity)由非线性函数的组合中产生,而不是传统的纹理映射或生长模型算法。基于以上思想,柏林(Ken Perlin)在1982年为《电子世界争霸战》(Tron, Disney 1982)工作期间,为生成自然的纹理效果开发出新的噪声算法,并于1985年正式发表,即柏林噪声。柏林认为一个好的随机函数应当具有以下特征:
1) 旋转下的统计不变性。无论怎样转动它的域,它都具有相同的统计特征。
2) 频谱上的窄带通限制。它在一定狭窄的尺寸范围内没有过大或过小的可见特征。
3) 变换下的统计不变性。无论对域进行怎样的变换,它都具有相同的统计特征。
对于柏林噪声,它还具有噪声数值连续、没有间断点的特点。1989年Perlin与他的学生Hoffert使用基于柏林噪声的Hypertexture来模拟火球。柏林噪声也是如今游戏内生成地形、模拟火焰、云雾、水面等的方式之一。柏林本人也因为柏林噪声算法的贡献获得了1996年美国电影艺术与科学学院的奥斯卡科学技术奖。

2.2 具体算法
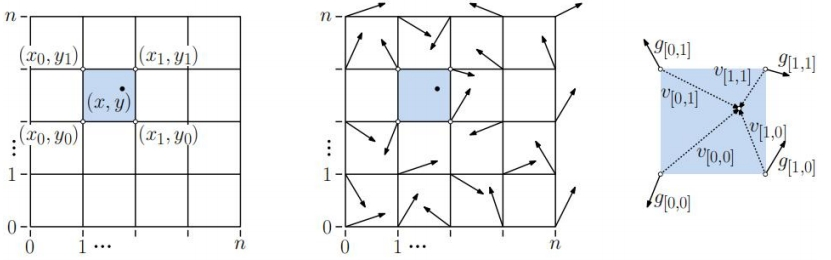
以二维柏林噪声为例。在空间平面内划分网格,赋予每个网格顶点一个随机的方向向量g[i,j],作为该点的梯度值。任取空间平面内一点(x,y),该点的噪声值,即为该点到四个顶点的距离向量v[i,j],分别与四个顶点的梯度向量做点积的结果。其中距离向量为
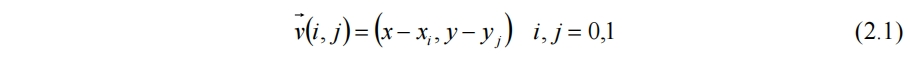
当(x,y)在网格内连续移动时,点积的值将平滑变化,因此噪声值也会平滑变化。
仅有距离向量并不够,还需进行加权:
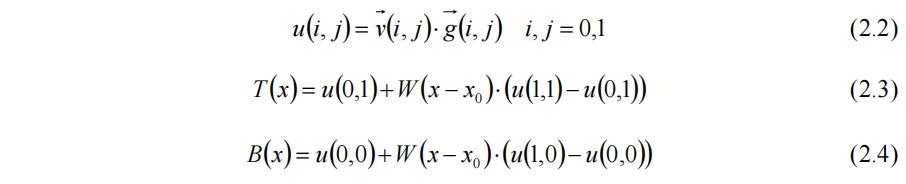
其中W为权函数。二维柏林噪声的加权结果为
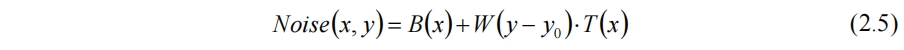
权函数多取
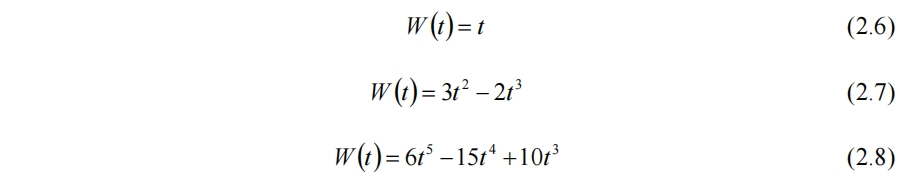
分别对应线性插值和光滑插值,又称缓和曲线(Ease Curve)。对于顶点的梯度向量,有的约束其长度为1,此处采用单位圆约束,即一个顶点的梯度向量应当位于所在网格的单位圆内。部分柏林噪声的实现为增强随机性还需指标随机化取模查哈希表,还有改进版Simplex噪声和分形柏林噪声等,此处不考虑。
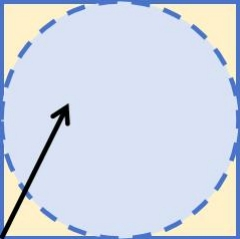
2.3 实现效果
2.3.1 1维静态柏林噪声
基于2.2节二维的算法,一维就是一条直线,不考虑单位圆约束条件,结果如图
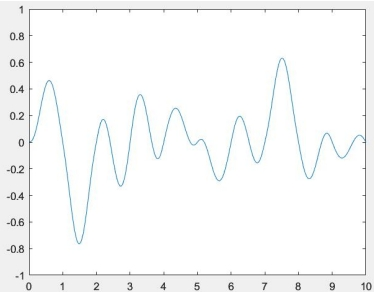
2.3.2 2维静态柏林噪声
二维实现方式与2.2节算法相同,采用单位圆约束。结果如图
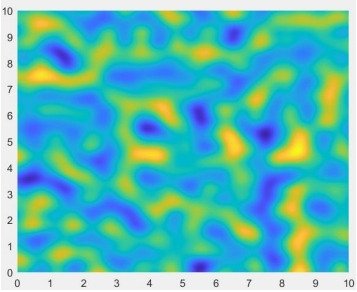
2.3.3 1维动态柏林噪声
一维动态柏林噪声是一系列一维柏林噪声沿时间方向推进演化的结果,需要额外增加一个时间变量并循环不断输出。
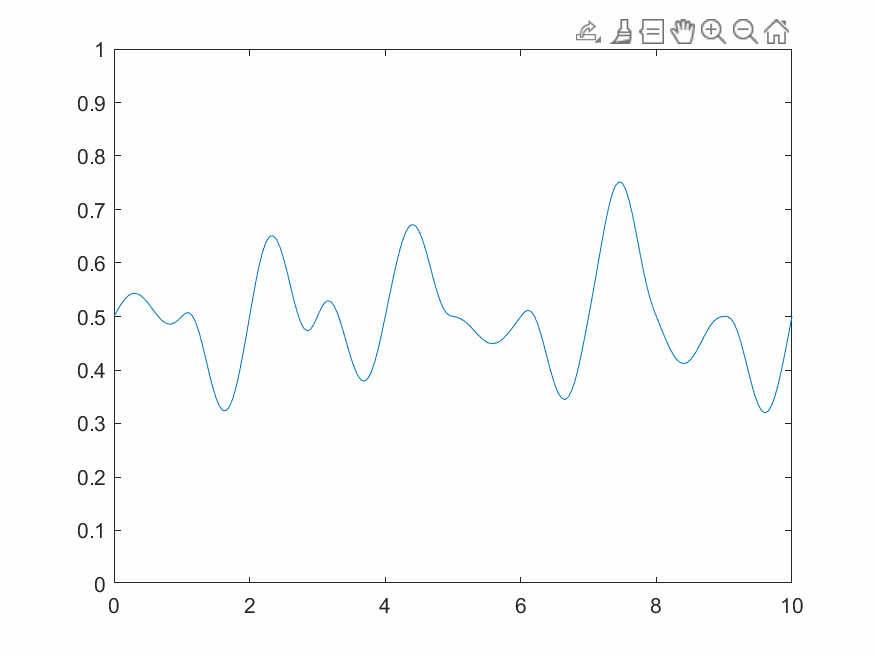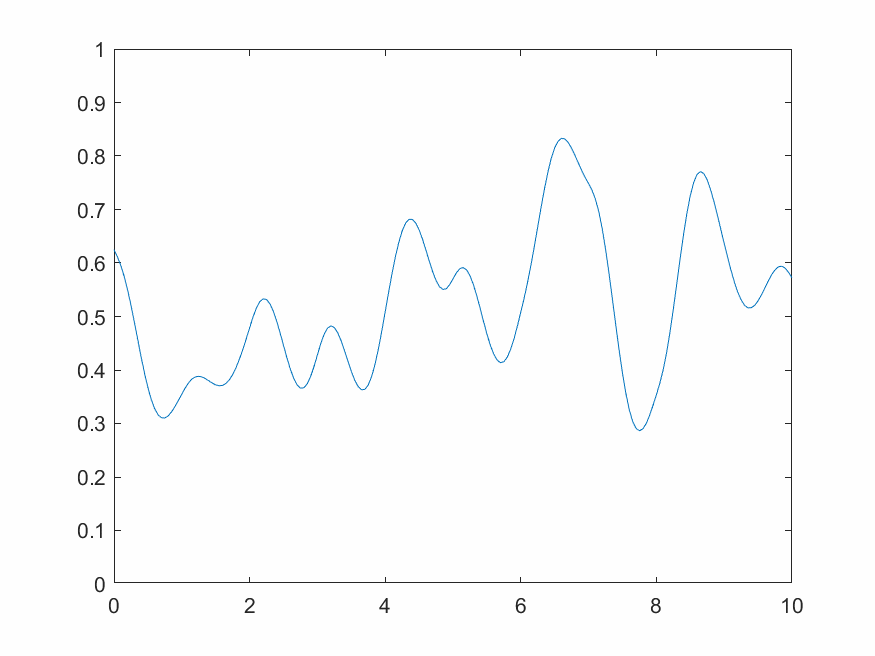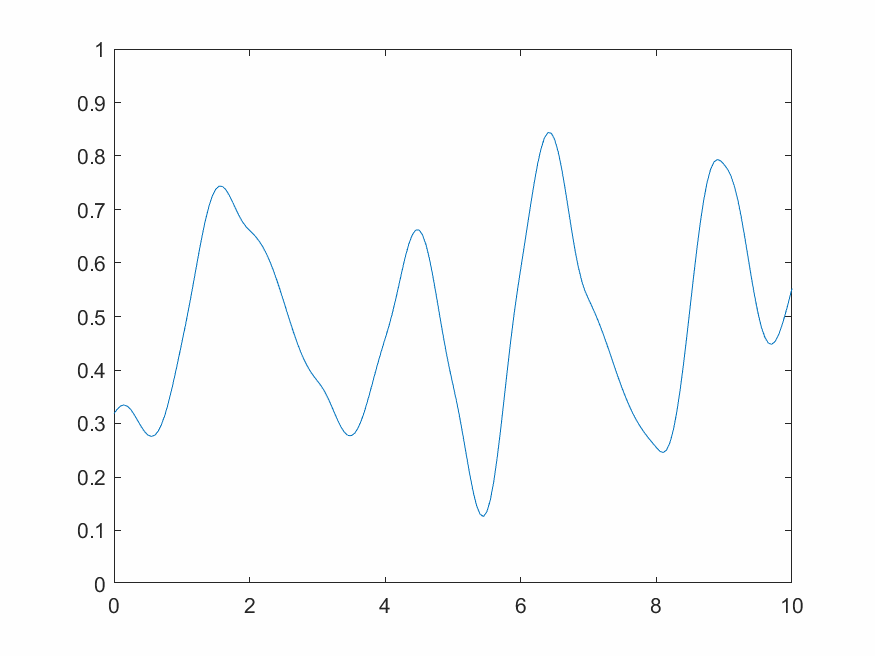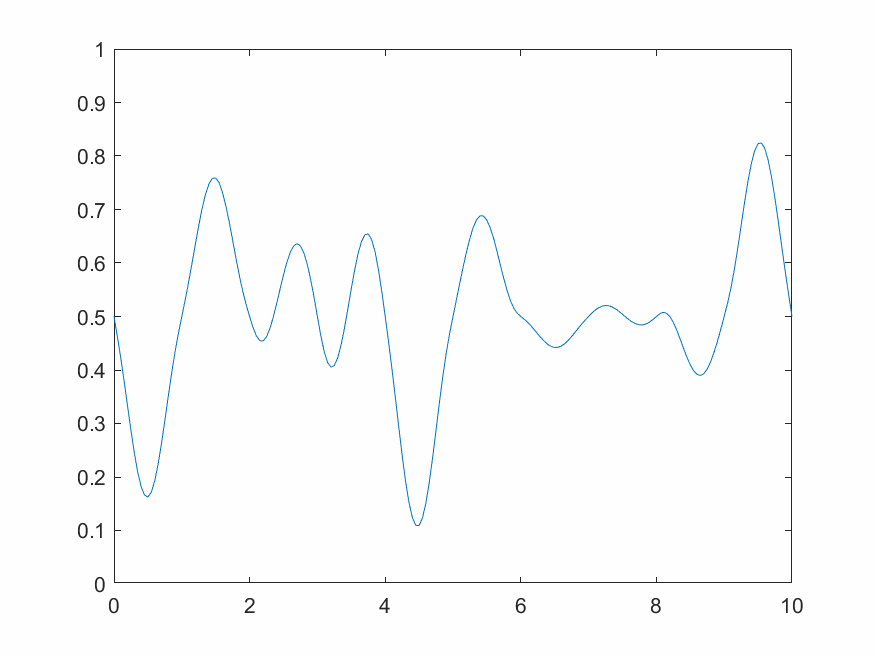
3 小波变换
3.1 基本思想
3.1.1 何为变换:Sam Porter Bridges
在死亡搁浅送快递的路上,动力装甲电量即将耗尽。恰好注意到前方高地处有一个充电桩,而山姆身上带着两把折叠梯。

此时大多数玩家的做法会是:向前方高地搭一个梯子,爬上高地到无线充电桩范围内充电,再搭一个梯子继续前进(也可以从原梯子处原路返回)。
变换就是Bridges。因为要充电,所以需要到高地,但又不能瞬移,所以需要经过梯子过去。梯子就是变换,充电就是对经过变换的东西的操作/处理,而再次经过梯子前进或返回就是逆变换。
3.1.2 傅里叶变换和短时傅里叶变换
变换的目的是用一组确定的简单函数来表示复杂函数f(t),其中确定的简单函数就是基函数φn。对于正交基有
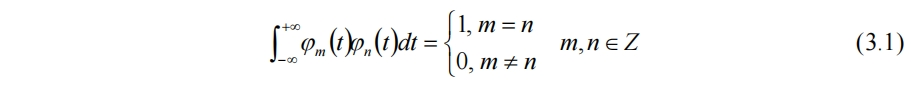
此时f(t)可表示为
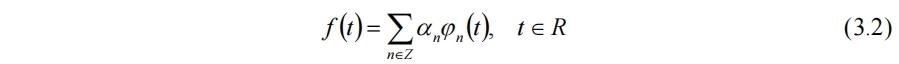
系数为
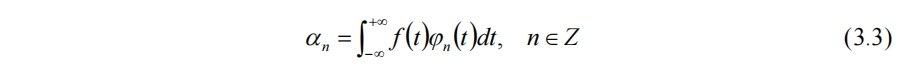
因此f(t)就可以唯一用αn来表示。周期函数进行傅里叶展开时选取的基函数为三角函数,对于非周期函数可视为周期T→∞,有傅里叶变换
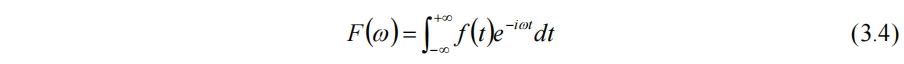
经过傅里叶变换,时域的信号被变换至频域,能看到该信号中各种频率分量的含量。但对于非平稳信号,频率分量会随时间变化,而傅里叶变换只显示该信号含有哪些频率分量,但并不提供这些频率在何时出现的信息。这对于分析非平稳信号很不友好。并且用傅里叶变换得到的结果在时间上是全域的,它不能提供信号变化的局部图像。
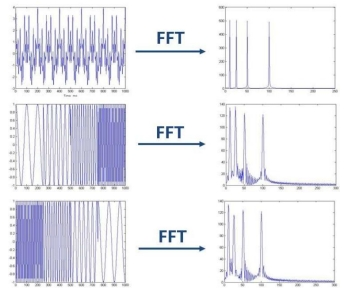
为了克服这一缺点,Dennis Gabor在傅里叶变换中引入窗函数w(t),建立起短时傅里叶变换(STFT,也称窗口傅里叶变换)。此时使用一个窗函数在一个区间内提取数据,再计算该窗口部分的傅里叶变换。因此STFT可以捕捉到信号中的瞬时响应。
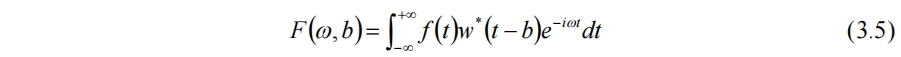
其中w*(t)为w(t)的共轭复数。对于窗函数w(t)还有其他限制,如窗函数在时域和频域的半宽度满足海森堡不等式
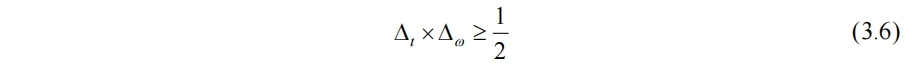
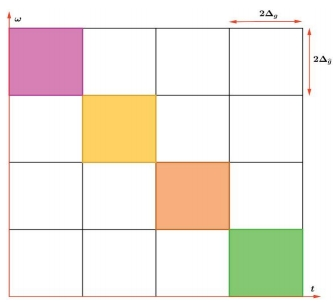
窗函数一旦确定,窗口的大小和形状就固定不变,其分辨率也随之确定。如果窗口取的较短,对于波长大于窗口宽度的低频区域,在频域的分辨率非常低。如果选一个长窗口,能量在较长的窗口宽度内被平均分配,它在高频区域时域的分辨率就很差。因此,如果一个信号由短时间的高频和长时间的低频组合而成,那么窗口函数就无法捕捉全该信号的重要信息。从(3.6)也可看出时域分辨率和频域分辨率的矛盾性。
3.1.3 小波变换
为了进一步弥补STFT的缺点,小波函数应运而生。在最简单的意义上一个小波可以被定义为一个衰减速度快且平均值为零的波函数。
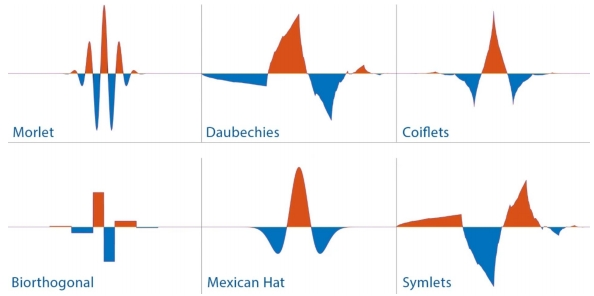
小波变换表示局部的时间和频率信号,它比傅里叶模式更能有效地检测间断点。它的形状可以改变,在捕捉较低频率时变宽,而在捕捉高频时变窄。
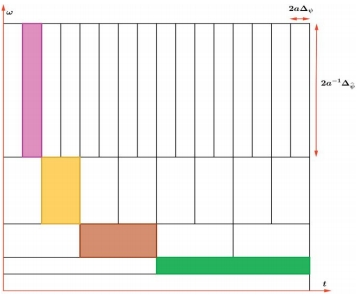
小波变换仍沿用STFT中的瞬态窗口,但随着频率的增加的同时,增加时间分辨率,即令带宽与频率成正比。选定一个小波函数ψ称为母小波,通过对其伸缩和平移可生成一系列小波:
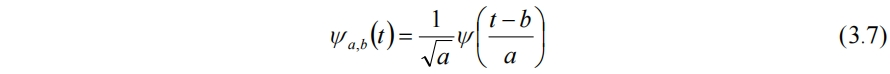
与窗函数对比,可见小波函数除了平移参数b,还有另一个可调的尺度参数a,因此能够实现窗口的改变。而连续小波变换为
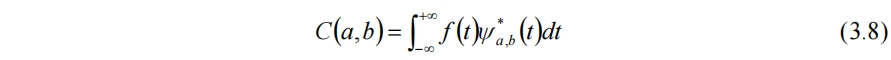
连续小波变换存在一些缺点,如冗余和不实用的问题。而离散小波变换解决了连续小波变换的不足。常用方式为将(3.7)中的a和b分别取
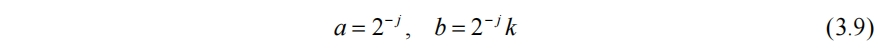
此时小波离散为
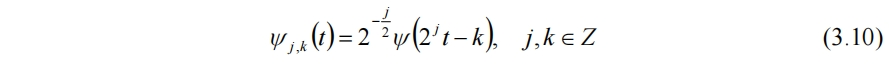
对应的离散小波变换为
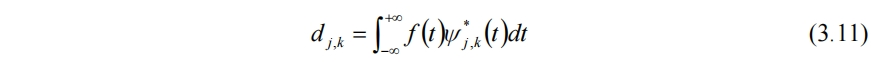
其中dj,k是小波系数。若小波系列能构成L2(R)空间的正交基,f(t)可重构为

许多经过小波变换的函数在转换到小波域时显得稀疏,很多系数都在0附近,因此小波变换常被用于数据去噪、图像压缩等领域。小波还有很多其他数学基础涉及到泛函分析、群论等,非所学专业不再展开。
3.2 尺度函数、小波函数和多分辨分析
以Haar小波为例引入小波变换中重要的基础概念:尺度函数和小波函数,介绍离散信号的多分辨表示。
3.2.1 尺度函数
对于信号x={x1,x2},定义其平均与细节分别为
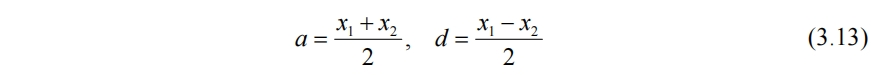
使用平均a与细节d重构信号,有
因此a和d是原信号x={x1,x2}的一种表示方式。
考虑分段离散信号f(t)如图,
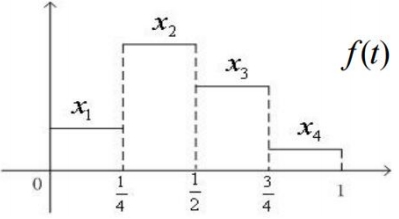
第一次取平均和细节
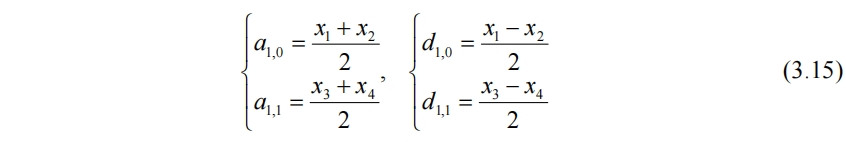
对于a1,0和a1,1还能再取一次平均和细节
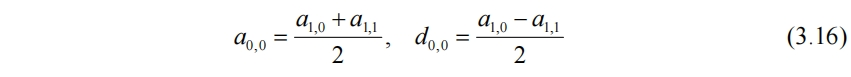
同样,原信号也可以由a0,0、d0,0、d1,0和d1,1重构回来。
对于图3.7的信号,考虑使用最简单的常数函数来拟合。定义尺度函数
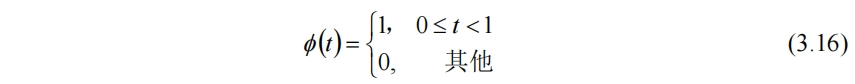
图像如3.8所示
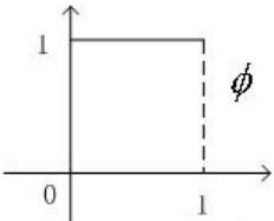
若要拟合f(t),需要尺度函数的区间更短,如果Φ(t)只在[0,1/4)上那么f(t)的第一段就可以表示为f1(t)=x1Φ(t),t∈[0,1/4),第二段可视为Φ(t)在[0,1/4)上向右平移1/4个单位再与x2相乘。因此对尺度函数Φ(t)进行伸缩和平移变换(非标准化),有
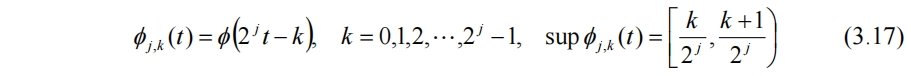
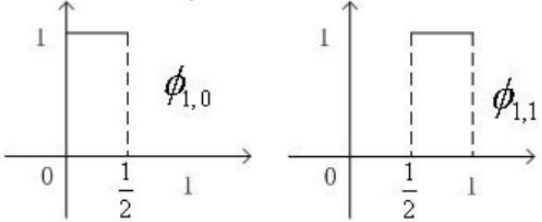
为描述f(t)需要Φ(t)伸缩2次、平移3次,此时
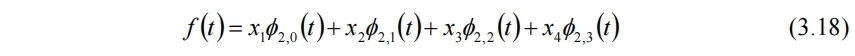
现在能够使用经过伸缩和平移的尺度函数描述原信号f(t),但还需原信号本身的信息x1~x4。能否使用平均信息a1,0和a1,1结合尺度函数来表示f(t)?
假设有g(t)满足要求,
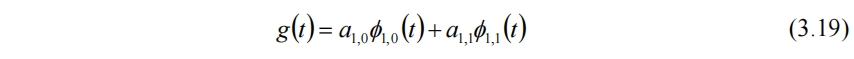
当t=1/8时,f(t)=x1,而g(t)=a1,0=(x1+x2)/2,并不相等。显然只用平均量a并不能重构回原信号,还需要引入细节量d。
3.2.2 小波函数
比较g和f的差别,可以发现g需要在[0,1/4)内加上x1/2同时减去x2/2,在[1/4,1/2)上相反,减去x1/2同时加上x2/2。而这加减的恰好是(3.15)式中的细节d1,0,只是在相邻两个区间内正负号相反。引入Haar小波函数ψ(t)
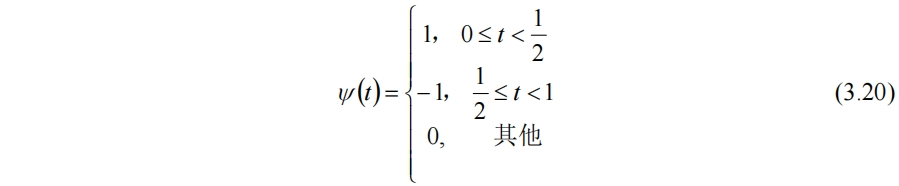
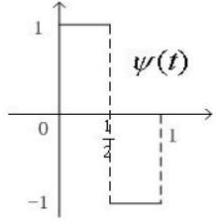
ψ(t)同样可以进行伸缩和平移(非标准化),
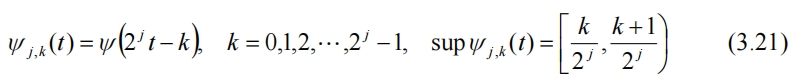
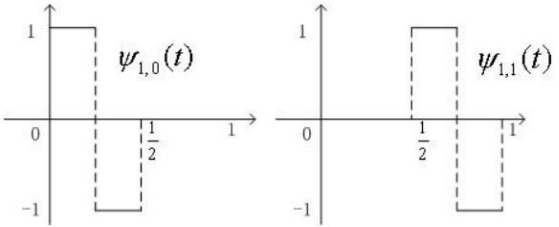
此时,f(t)就可使用平均量a和细节d,以及尺度函数和小波函数完整重构
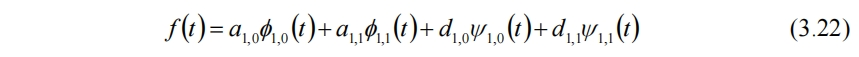
3.2.3 多分辨分析
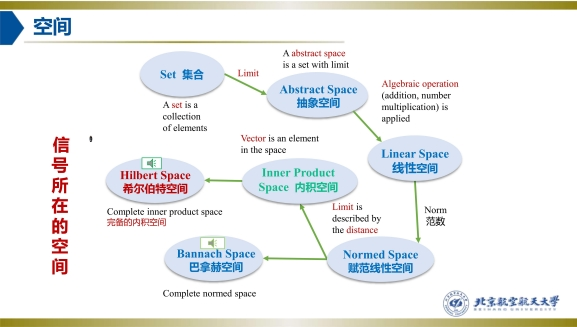
多分辨分析(Multiresolution Analysis)从函数空间特别是线性代数中内积空间、正交和、正交补、基等的角度出发进行分析。在尺度函数(3.17)和小波函数(3.21)伸缩平移的过程中,j每增加1函数就缩短为原来的一半,每次平移的分辨率就越高。而同一个信号,又可以用不同层级分辨率的尺度函数和小波函数来表示。如(3.22)使用第一层的平均和细节重构f(t),也可以使用第二层的平均和细节与第一层的细节共同重构:
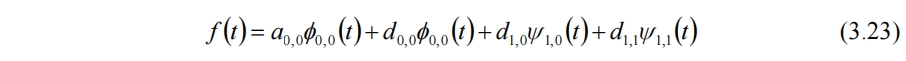
如果信号更长,还可以继续分解下去。
不同尺度之间通过两尺度方程联系。显然尺度函数和小波函数满足
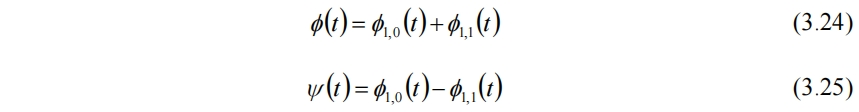
对于其他尺度同理。真正严谨的多分辨分析,还需参考教材深入学习。

4 2维火焰面和焦油面模拟
4.1 火焰面模拟
最基础的火焰形状在很多游戏中都出现过,如各种中世纪游戏中必不可少的火把,以及在黑暗之魂3(Dark Soul III, FromSoftware 2016)中常见的篝火火焰,可见基本形状与正态分布类似。
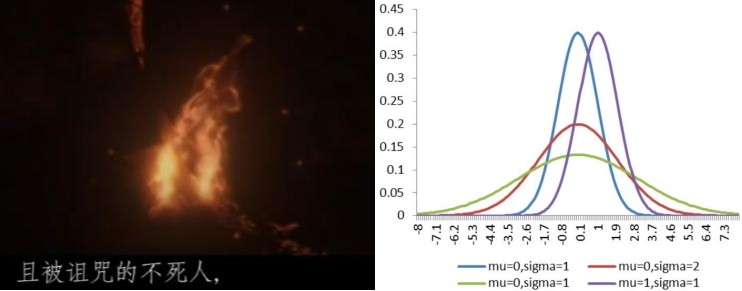
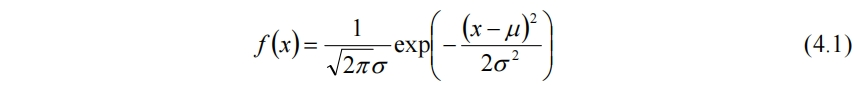
因此选择以正态分布函数为基底,线性叠加噪声来模拟湍流火焰的无序动态燃烧效果。参数a和b用于调控形状
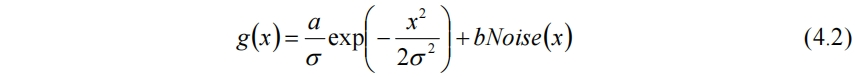
湍流火焰锋面应当尖锐、粗糙而非光滑,可以考虑用柏林函数在低分辨率下线性插值,不做小波变换。火焰具有分形特征,也可以考虑对光滑表面做Daubechies D4小波变换构造分形火焰面。对于蒸汽朋克世界,如果处处都是齿轮,连火焰面都是锯齿也未尝不可,此时可以使用Haar小波变换。结合麦克斯韦的弹性齿轮、惰轮电磁场模型,可以从底层的齿轮架构电磁场开始构造纯正的齿轮蒸汽朋克世界。
4.1.1 小波变换效果
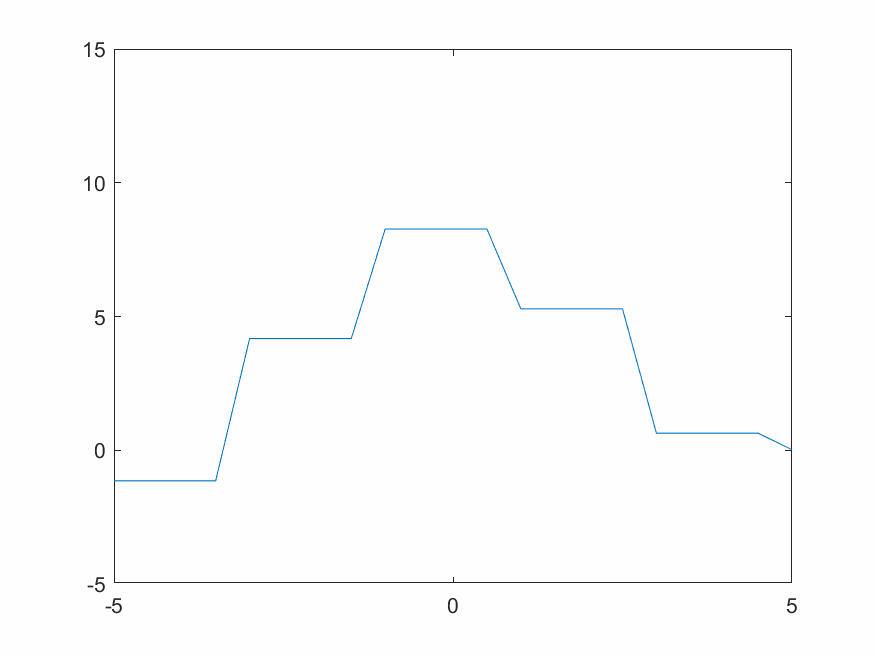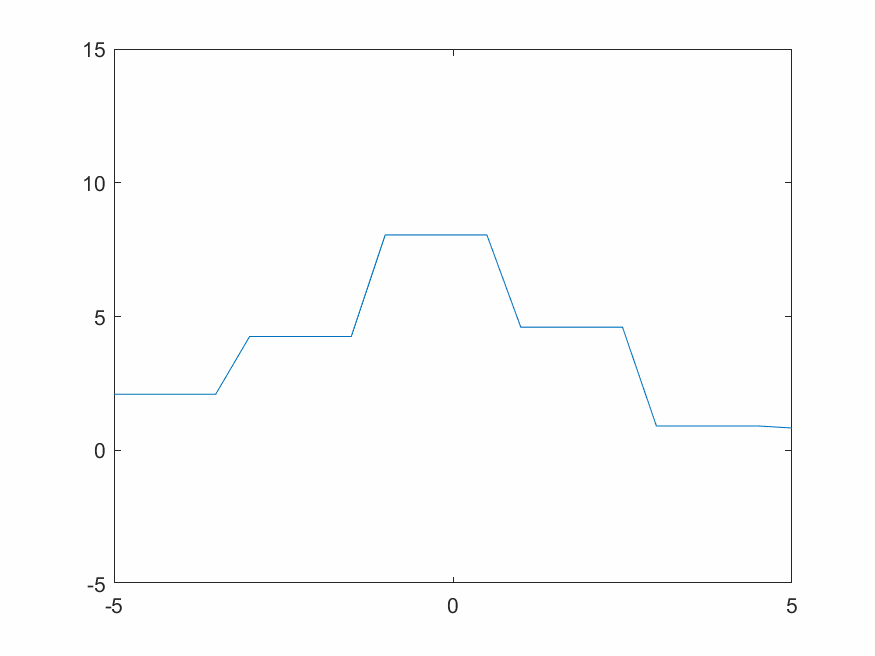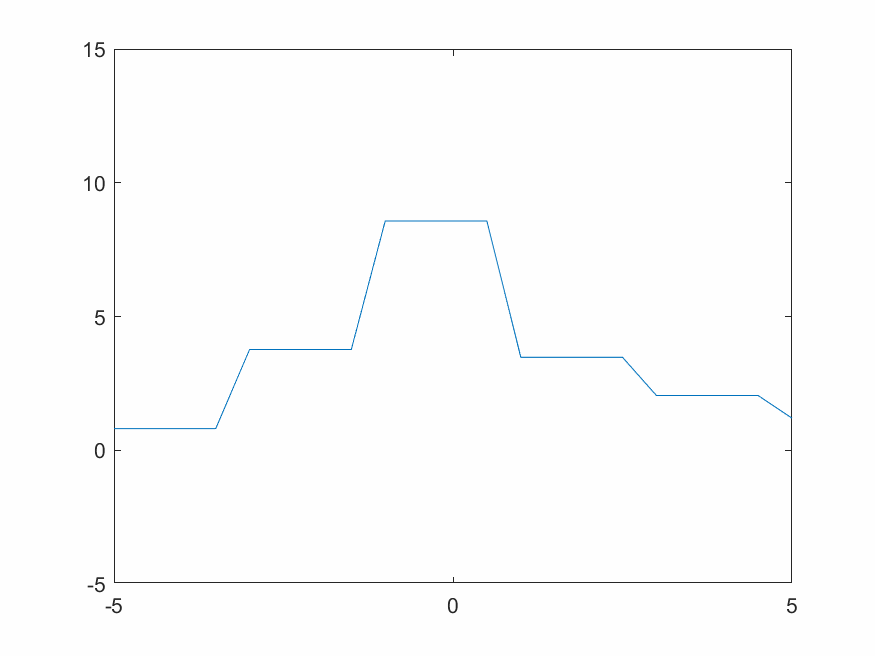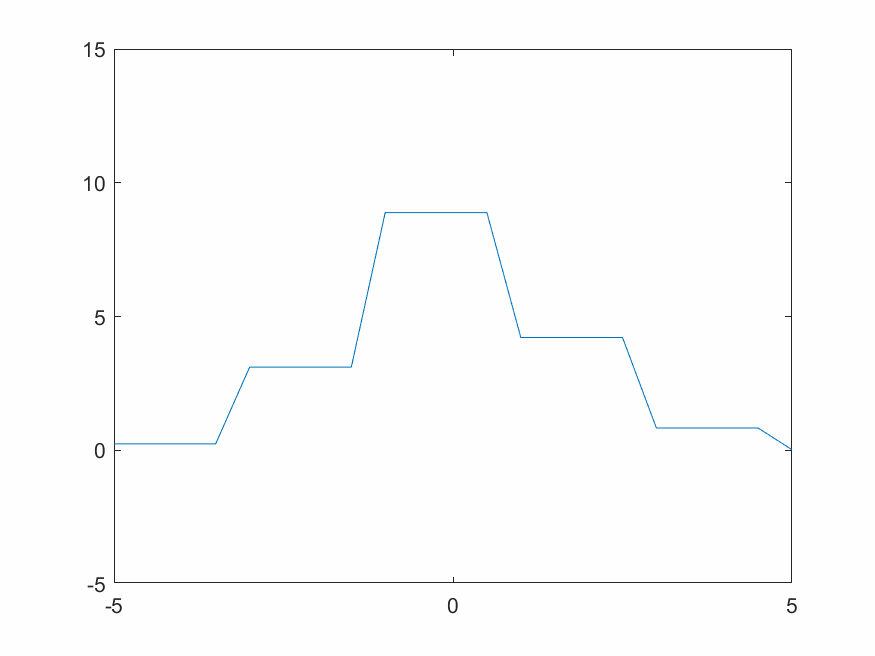
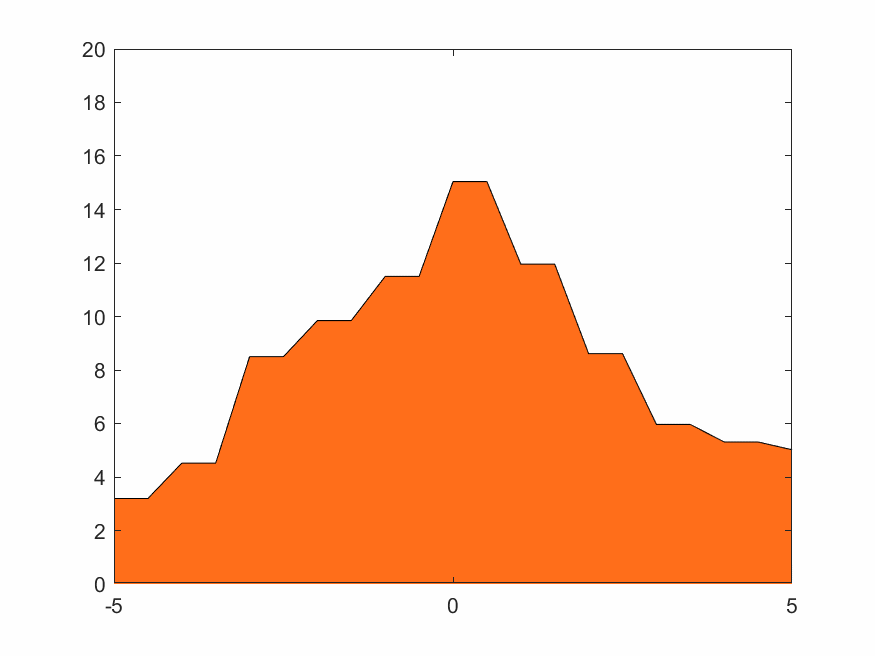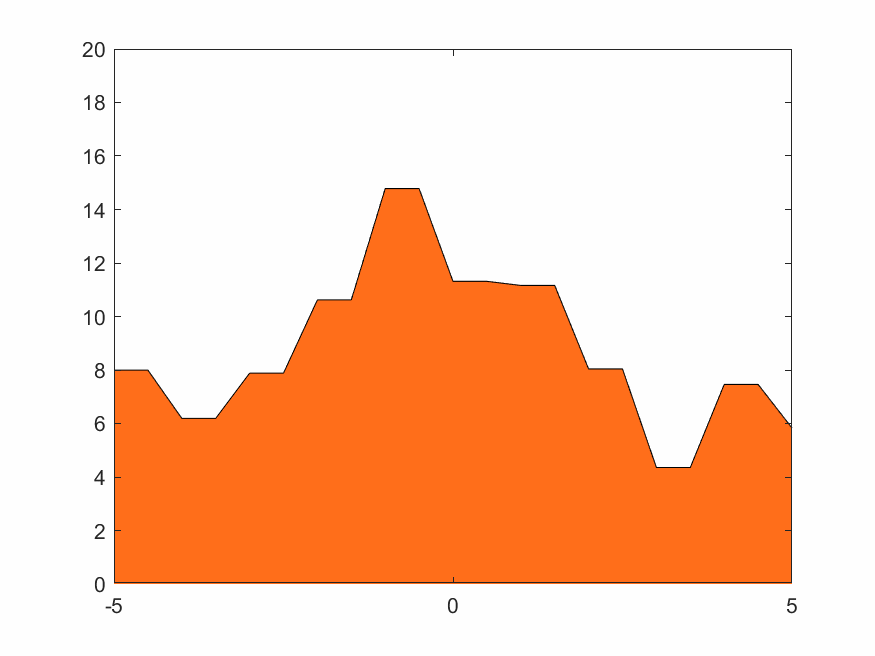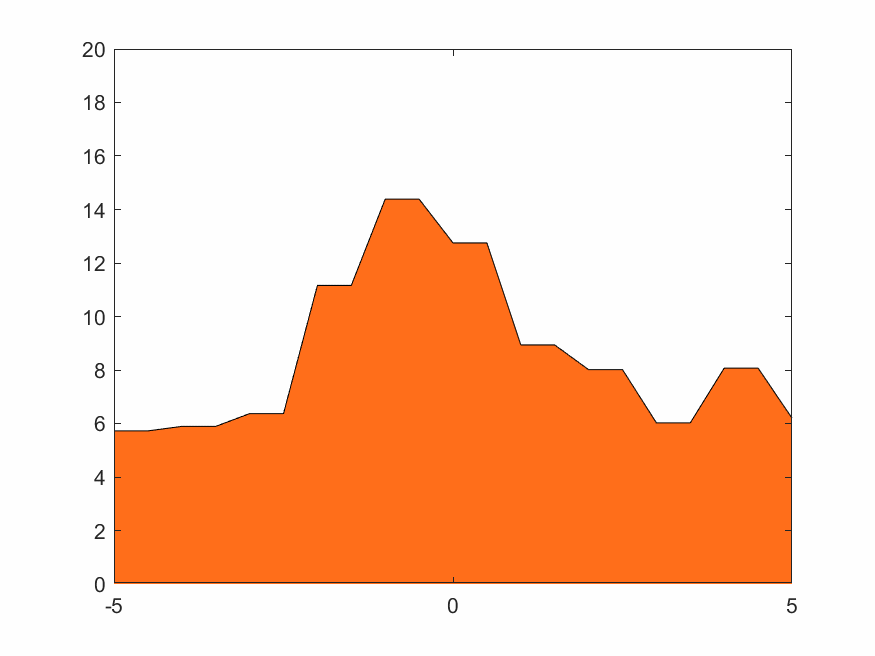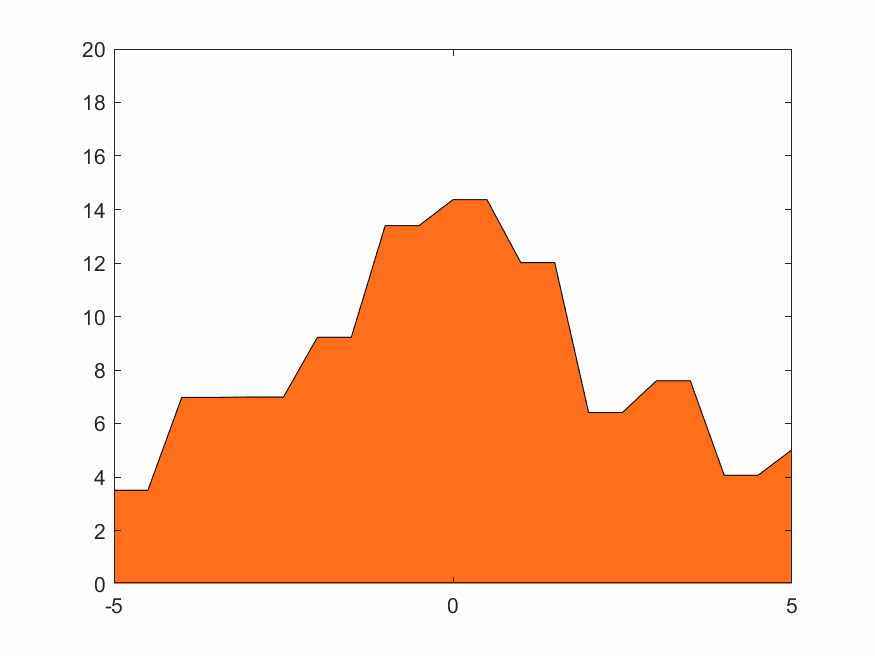
对于一个固定的柏林噪声波形,选择不同小波进行变换有不同效果。xy分辨率较低时去掉细节会使整体波形更平缓。用同样的细节层数重构,光滑小波比不光滑的小波重构出来的结果显然更光滑。图4.2~4.4的xy分辨率为0.5,使用线性插值。
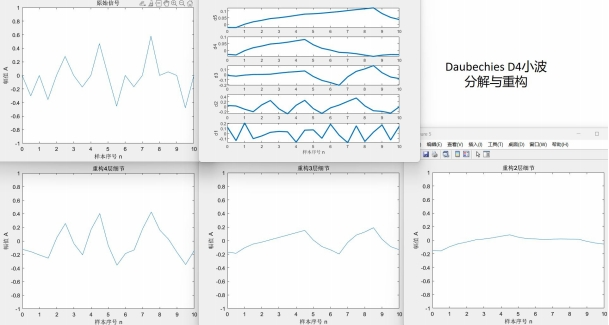
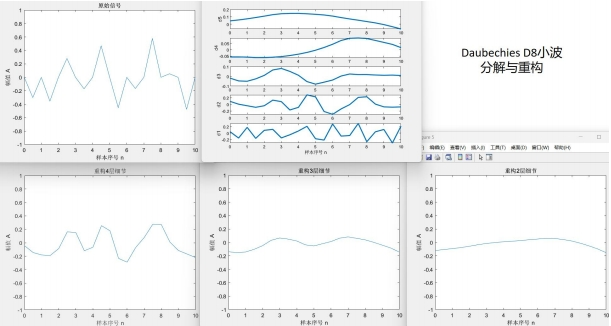
D8小波比D4小波更光滑,从下方三张重构结果图片也可看出D8重构结果比D4更光滑。Haar小波本身就是锯齿形,重构出来的波形也一定有锯齿特色。这也是适合蒸汽朋克的原因。
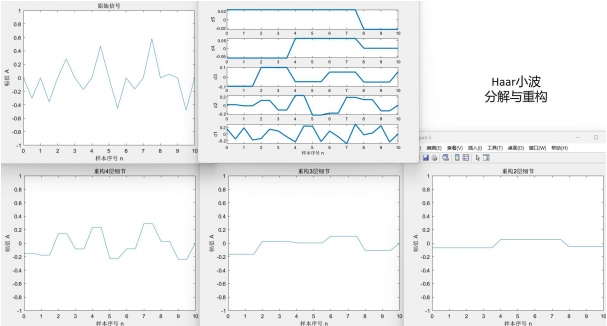
而在高分辨率下,结合多项式插值,波形本身比较光滑。用不光滑的小波重构,其去掉细节的平均量会使波形变粗糙,向所使用的小波函数靠拢。图4.5~4.6的xy分辨率为0.05,可见去掉越多的细节,D4小波变换后的结果越粗糙。而本身光滑的Vaidyanathan小波效果相反。
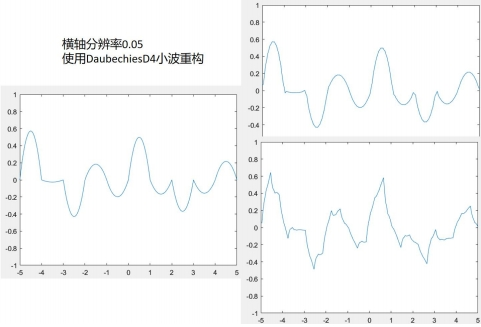
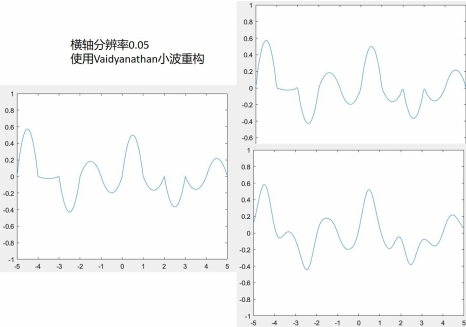
因此对于火焰模拟有以下方式,一是低分辨率不进行小波变换,也可以进行Haar小波变换,另一种是高分辨率进行D4小波变换。
4.1.2 低分辨率无变换火焰
在(2.3)~(2.5)式中的权函数取线性插值,即(2.6)式。结果如下
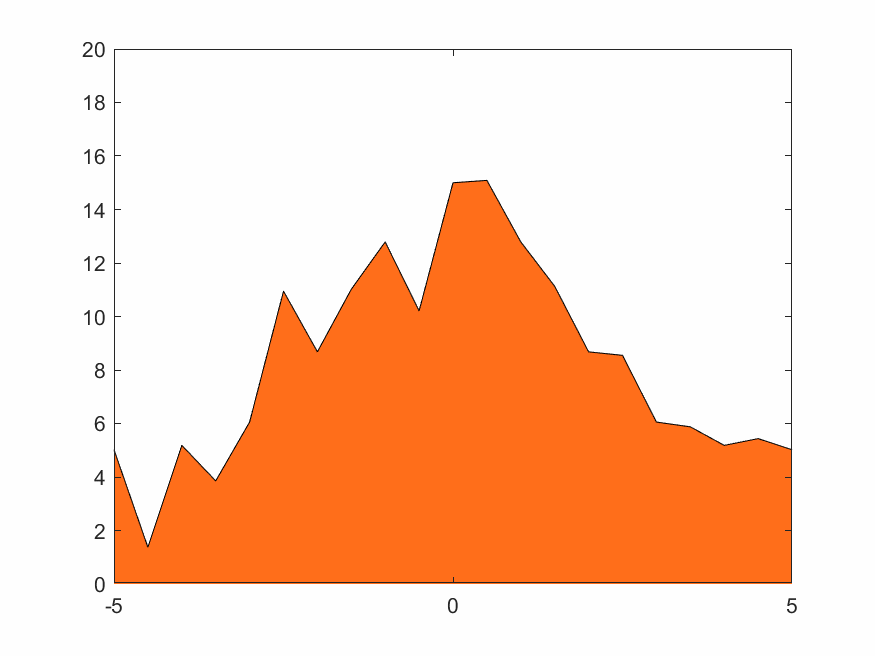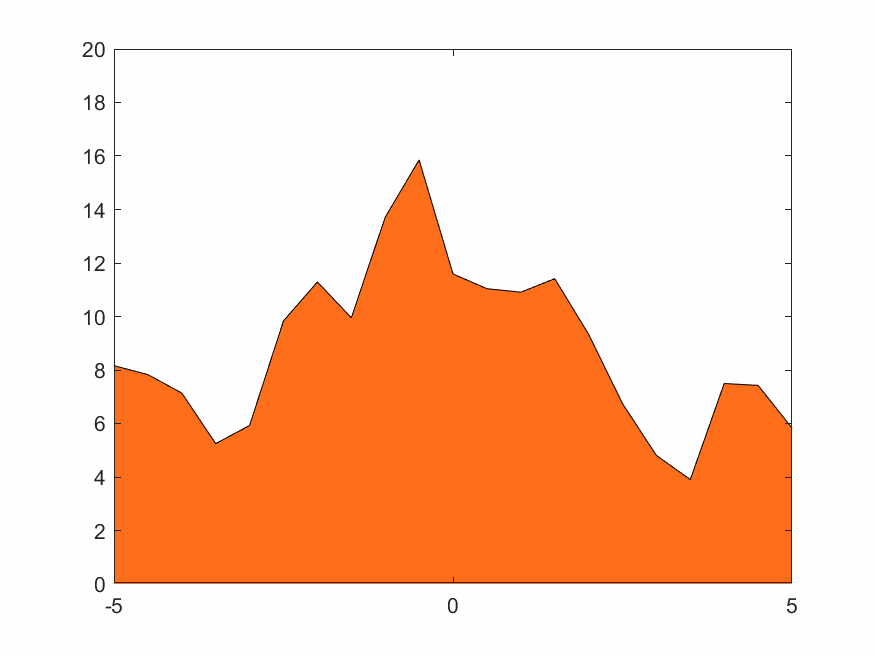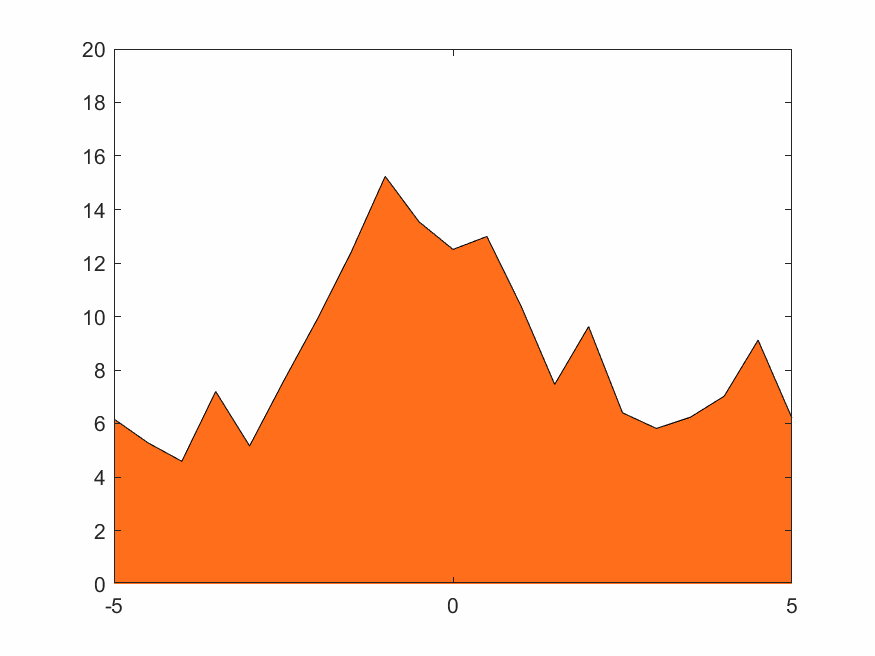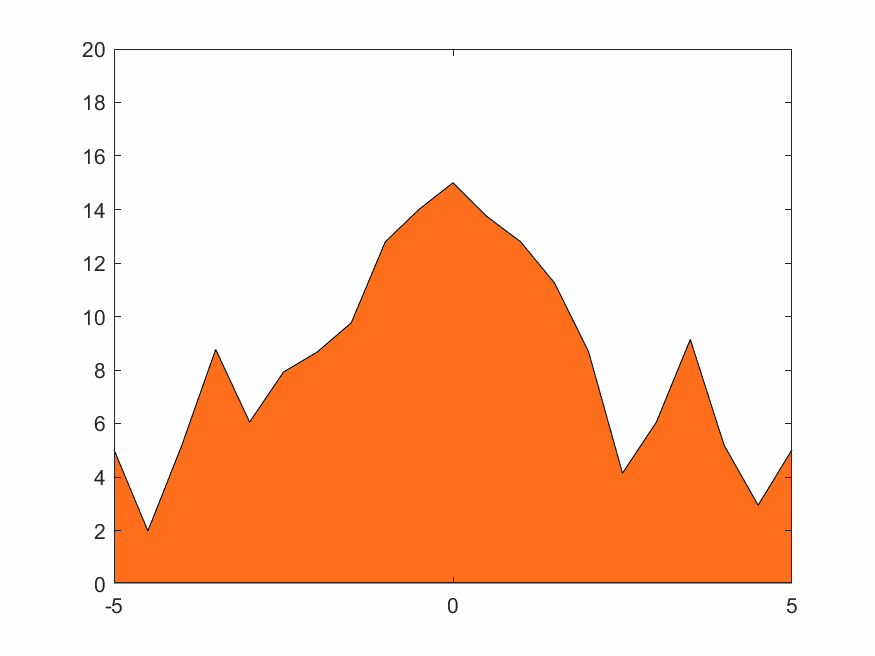
4.1.3 低分辨率Haar小波变换
Haar的移动城堡、蒸汽朋克下的锯齿火焰,效果如下
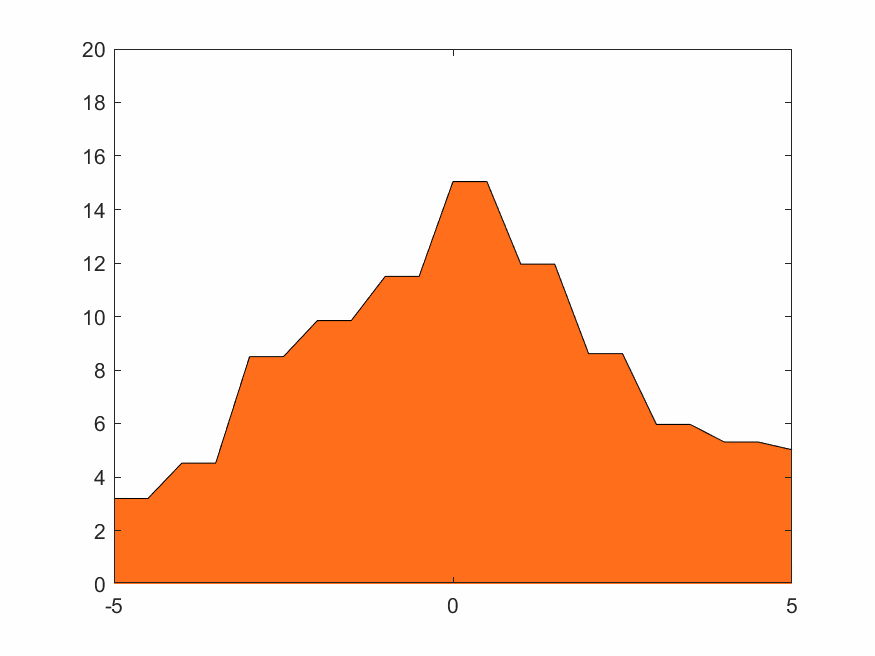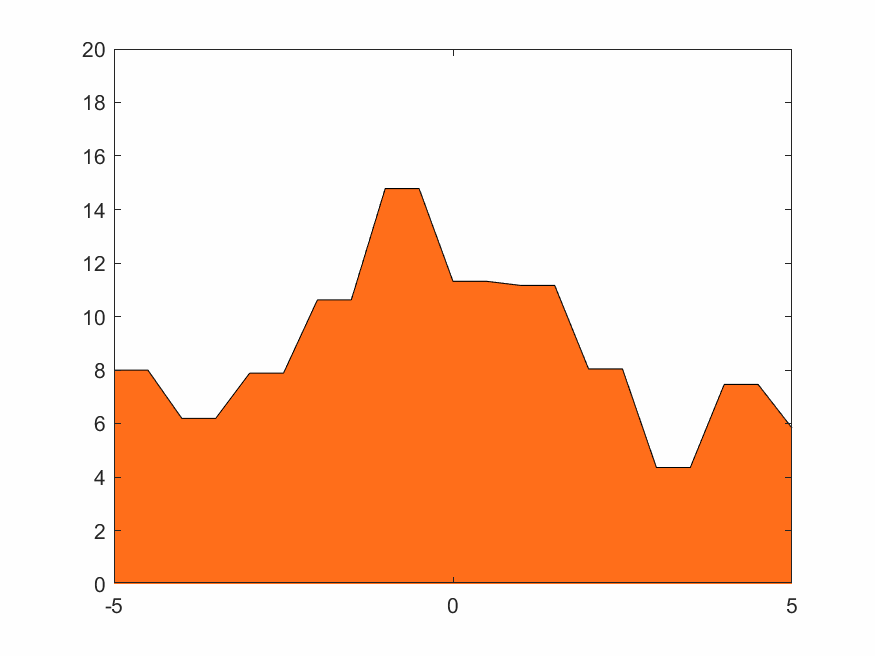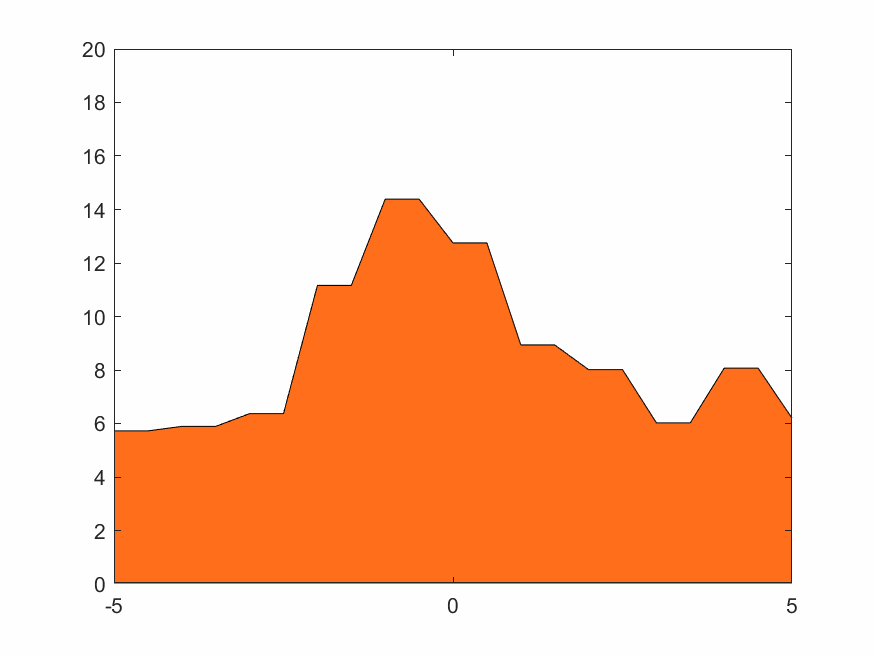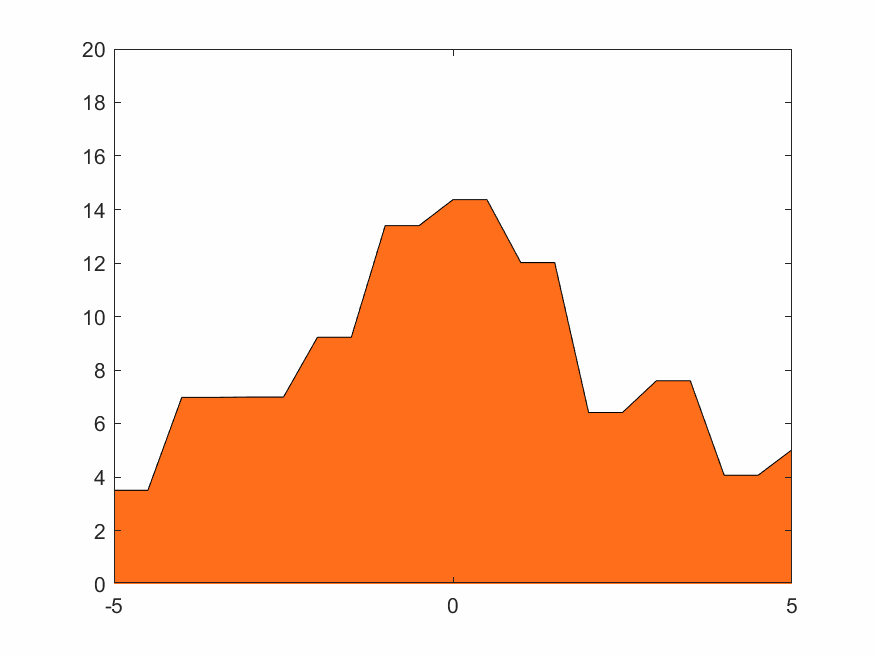
4.1.4 高分辨率D4小波变换
xy分辨率为0.05,权函数用(2.7)式,通过Daubechies D4小波变换去掉3层细节:
可见重构后的火焰也具有了分形的特点。但这样非物理的简单模拟出的火焰看上去还是不够自然。
由于正态分布函数在远离轴的位置函数值很小,而柏林噪声函数在整个范围内均值不变,因此火焰图像有比较明显的上下波动。可通过对柏林噪声项加入阻尼函数来解决这一问题。
4.2 焦油面模拟
正态分布函数的标准差σ可以控制其图像的分散程度,如果σ较大则图像扁平,适合模拟有表面张力效果的水面。此时柏林噪声为水面上的波动如起泡等。少量的冒泡需要限制柏林函数在区域两端的值,因此(4.2)式改为
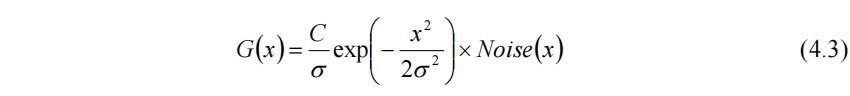
这样的水面模拟和火焰面模拟具有同样的问题,与上篇文章所述的浅水方程类似,自由表面都使用了表面函数假设的限制,同一个x位置不能出现两个函数值,因此无法模拟真正的起泡脱离表面、海浪卷起等效果。还可以将焦油面和火焰面结合,实现燃烧的焦油面效果,因为二者完全可以共用一套随机数。

对不起,做不到
记
关于物理真实和视觉真实的讨论,可参考上篇水体模拟中的“记”,Fournier和Reeves有相当精彩的论述。此外Ebert等仍强调,"For entertainment applications, empirical accuracy is not the goal; visual verisimilitude is, and visual novelty might prove even more useful."
对于火焰模拟和水体模拟的区别,Lamorlette和Foster指出:"Fire on the other hand, is a dramatic element that requires the maximum level of control possible while maintaining a believable appearance. We expect fire to look complex and unpredictable, while at the same time having a recognizable structure according to the conditions under which it is burning. That complexity by itself makes direct numerical simulation of fire much less attractive than for other phenomena..."令人信服的火焰外形应当是不可预料的,但火焰动画又必须可控,按照艺术创作者的需要绽放。所以它不能是纯物理的,这样对创作者而言就缺少调整方式;它也不能是纯动画的,这样太不真实。本篇实现的分形火焰虽然看着像个火焰,但很缺乏真实性。也许基于上述内容可以加入一些物理的模拟构造出更逼真的效果。而焦油模拟的效果显然比火焰要好,实际上这两个效果都是基于完全相同的随机数种子生成的(取消了随机数生成器,改为输入一组固定数据)。这也是Lamorlette等看法的又一印证。
实际上在D4火焰效果实现后发现,早在2009年工业光魔公(Industrial Light & Magic)的两位研究员Horvath和Geiger就已经将小波变换引入计算机图形学的火焰模拟过程:We augment the PIC/FLIP technique by using a simple wavelet decomposition on the velocity grid to produce multiple levels of detail. This allows us to amplify vorticity at multiple scales as well as accelerating convergence of the iterative incompressibility solution.他们的思路也是使用小波分解来增强火焰的细节,但包含物理求解不可压NS方程的过程,也有一套具体实现方案。他们使用NVidiaQuadro5600 GPU,每个切片的每一帧平均需要20秒来模拟。使用10个GPU,模拟通常需要2到4个小时,渲染需要另外的1到2个小时。实现结果如图。
同样使用了小波变换,但不得不说Horvath和Geiger的实现结果与按本篇方案的效果相比简直没法比。

游戏创作就是艺术创作。不仅如此,更底层的计算机图形学也是艺术。Musgrave、Peachey和Ebert等对梵高、修拉的绘画作品与计算机图形学进行对比:"Good painters evoke worlds of color in a painting, and even in a single brush stroke. Van Gogh, who painted with a palette knife, not a brush, executed several paintings in the morning, took a long lunch, then did several more in the afternoon. Painting in a hurry, he didn't mix his paints thoroughly before applying a thick blob to the canvas. Thus each stroke has a universe of swirling color within it. Seurat's pointillism is another form of what painters call juxtaposition, or the use of a lot of different colors to average to some other color. This is part of the visual complexity that, to me, distinguishes good paintings from most computer graphics."
确实,好的画家用一幅画,甚至一笔就能向观众唤起一个色彩的世界。如今AI取得了前所未有的飞跃,但距离真正的人、创作的人、理性的人、游戏的人,还差得远。

参考文献
[1] Ten Lectures on Wavelets, Ingrid Daubechies
[2] 《小波变换》课件,BUAA王海辉教授
[3] An Image Synthesizer, K. Perlin
[4] Hypertexture, K. Perlin, M. Hoffert
[5] Depicting Fire and Other Gaseous Phenomena Using Diffusion Processes, J. Stam et. al.
[6] Interactive Simulation of Fire, Z. Melek et. al.
[7] Particle Systems-Technique for Modeling a Class of Fuzzy Objects, Reeves, William T.
[8] A Technique for Art Direction of Physically Based Fire Simulation, A. Bangalore et. al.
[9] Physically Based Modeling and Animation of Fire, Nguyen et. al.
[10] Breeding Terrains with Genetic Terrain Programming: The Evolution of Terrain Generators, Frade et. al.
[11] A Fire Flame Simulation Scheme with Massively Parallel Processing, Byeong-uk Im et. al.
[12] The Fractal Geometry of Nature, Mandelbrot
[13] Directable, High-Resolution Simulation of Fire on the GPU, Horvath et. al.
[14] Laminar Flamelet Concepts in Turbulent Combustion, N. Peters
[15] Improving Noise, K. Perlin
[16] Generating and Rendering Procedural Clouds in Real Time on Programmable 3D Graphics Hardware, Hasan et. al.
[17] Introduction to Wavelet Transforms, Bhatnagar
[18] Generation of Augmented Bathymetry to Aid Development of Terrain-Aided Autonomous Underwater Vehicle Localization and Navigation Approaches, Heubach et. al.
[19] A Parallel Algorithm Using Perlin Noise Superposition Method for Terrain Generation Based on CUDA architecture, Li et. al.
[20] Texturing and Modeling: A Procedural Approach, Ebert et. al.
[21] 小波变换与图像、图形处理技术,孙延奎
[22] Wavelet Analysis: Basic Concepts and Applications, Arfaoui et. al.
[23] Wavelet Transforms, Kith and Kin, Shah et. al.
[24] Wavelets and Wavelet Transform Systems and Their Applications: A Digital Signal Processing Approach, Akujuobi
[25] 形象易懂讲解算法I——小波变换,https://zhuanlan.zhihu.com/p/22450818
[26] 从傅里叶(Fourier)变换到伽柏(Gabor)变换再到小波(Wavelet)变换,https://blog.csdn.net/jbb0523/article/details/42028587
[27] The Art of Fluid Animation, J. Stam
[28] Structural Modeling of Flames for a Production Environment, Lamorlette et. Al.
[29] Combustion Physics: Flames, Detonations, Explosions, Astrophysical Combustion and Inertial Confinement Fusion, Liberman
[30] Gas Turbine Combustion: Alternative Fuels and Emissions, Arthur Lefebvre
尾
及格再放代码,不及格就重修
