那麼，本次依然用如星光般璀璨的啦噗哩鎮樓。
這次，我們還能做什麼呢？我們回到正態分佈本身吧。這是一個非常和諧的概率分佈函數，當然也是一個運用率很高的函數。在之前的項目中，對於尋找特定準度區間裡每種不同判定的統計學分佈，我使用了正態分佈表，所以對於根據這個得到的σ值再帶入表的結果，當然是個估計值，雖然說不會差特別多，但是一個一個對著找也蠻麻煩的。而且這個方法也不可能覆蓋更多的準度精度，上次我也僅僅是以5ms為間隔做了一個表。能不能更自動化一點？當然是可以的。總不可能沒用過最著名的數據處理軟件Excel吧？其中很多人並不一定使用過公式和函數功能，就算用過可能也只是求和平均，再高級一點可能也就算個方差啥的。在Excel裡有沒有跟正態分佈相關的函數？
還真有。隆重請出函數NORM.DIST和NORM.INV。如果你對算數統計啥的看著就想吐，這一段建議別看，後面有懶人包的。對於NORM.DIST函數要輸入4個參數，除了最後那個選擇是輸出累計分佈還是概率密度的量（這次我們要用的是前面那個），剩下的只要輸入要求的分佈的數值x、正態分佈的平均數μ以及標準差σ，就可以得到跟正態分佈表裡一樣的結果。就和我上次說的一樣，輸出的是（-∞，x）的累計概率分佈。在我們一開始的假設情況裡μ=0，也就是平均準度正好在絕對正確的時刻，而σ在數值上等於我們之後要算的準度區間的1/3。有這個函數之後只要改變σ的值，把x設為大p的判定範圍70ms，就可以得到上次那個表的結果了。
那麼既然有這個函數了，能不能反過來根據已有的TP值來得到更精確的準度區間的結果？答案顯然是可以的，這個就要用到另一個函數NORM.INV了，但是具體這個函數怎麼用，我想先賣個關子，讓我們把目光放在另一個話題上。
那就是4.7版本新增加的嚴格判定（master）模式。
啥你還不知道這是個甚麼玩意？長按紫譜難度的圓圈就可以切換到這個模式，一個膠囊解鎖一首歌的嚴判模式。需要注意的是隻有紫譜和綠譜才能使用這個模式來打歌。不要再問為什麼紫譜打歌要花膠囊了，也不要再問為什麼自己打過的歌分數突然沒了。（雖然後面那個問題更大的可能是因為被某個黑客駭了……）
上次我還引用了某個九把七雞五連雞的主播（還有幾天就到一週年紀念了）的名言：分數沒有意義，快樂才是真諦。然而在嚴判模式下，就不是分數沒有意義這麼簡單了，分數直接沒有了。取而代之的是一個更高級的TP標準：M.TP，並引入了一個更嚴格的判定：master，這個判定比之前我們見過的大p（官方說法叫c.perfect）更嚴格，所以沒準會看到神仙說出“爆大p”這種以前想都不敢想的說法。順便說一句，假如在這個判定下打出全部都是master判定的成績，除了M.TP的結果必然是100之外，最後結算的評價會從正常的Million Master變成Max Master；不過啊假如連MM都沒有的話，那最後的評價只有一個簡單的Clear，畢竟已經沒有分數了。當然我們完全可以按照之前的玩法把這個新判定標準加入進來，最後轉換成M.TP的結果，可是還有一個小小的問題：
Master判定的區間是多少ms？
不知道。至少沒有一個非常可信的數據。不過我們可以自力更生，算嘛，反正現在的項目也是一直在算，不差這點功夫。現在只需要做的，就是按照正常的狀態去打幾遍歌，然後統計判定數據，再用已知的大p/小p分界線為70ms得到σ，最後用這個得到的值重新帶回累計概率的公式中，就可以得到我們算出來的m/大p分界線了。
但是選的歌也有一點要求，首先要保證點擊note的打擊難度相對均衡一點，最好不要出現前半段很簡單後半段非常難的部分。然後為了減小隨機誤差要多次實驗，這對於理科生的我來說已經是基操了。最後數據相對好看的是這兩首：
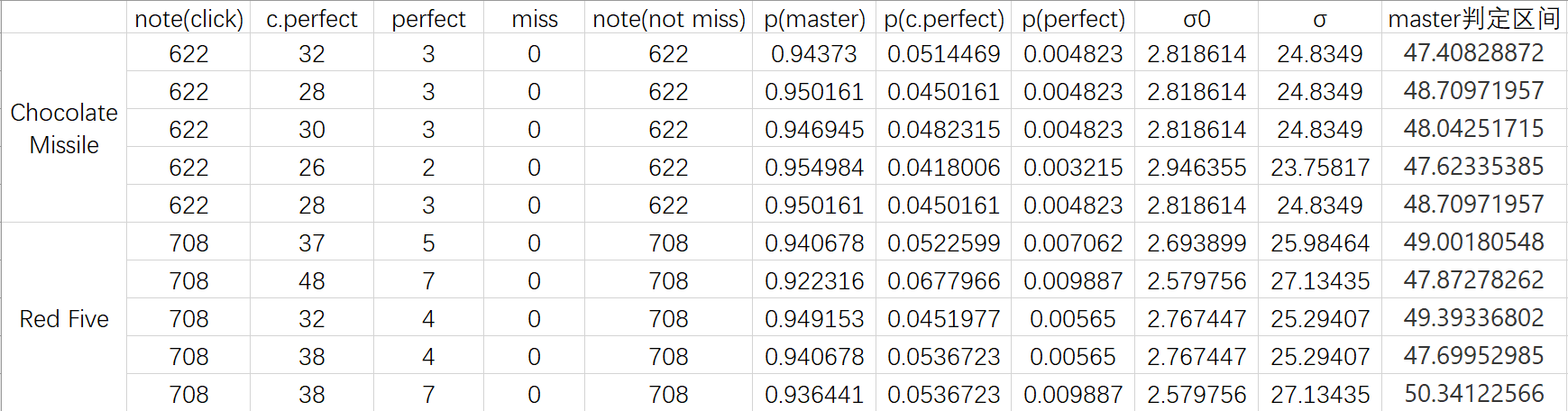巧克力導彈打的是綠譜。解釋一下一些列是什麼意思，note（click）表示除了只有最高判定的note之外的note總數（點擊劃鍵和點鎖頭），這裡不能像上次一樣估一個低判定note比例，我需要更精確的比例。σ0是用之前提到過的NORM.INV計算出來的，它和標準公式裡的σ意義不一樣，因為NORM.INV提供的參數是累計概率p、正態分佈的μ和σ，得到的結果是在這個累計概率下對應的正態分佈的數值x。這個概率我們就選大p以上判定的頻率，也知道這個位置對應的是70ms的位置的累計概率。但是我們怎麼知道在這個位置是70ms的前提下，正確的σ值是多少？接下來的一個思想比較重要，之後也會用到：我們完全不需要關心正態分佈的絕對σ值究竟是多少，只需要關心要求的累計概率的絕對位置與σ的比值，也就是相對σ值即可。所以這個參數設成1也沒有任何問題，所有正態曲線都是相似的，只要縮放一下就OK了。這樣得到的這個二點多的σ0值，我們已經認為這個也就是70ms，接下來就用70除以σ0，就得到了之前提到的正確的σ值，用這個σ值反帶回到NORM.INV的參數σ裡，得到的結果必然是70。最後用這個值，再用一次NORM.INV函數，這次我們的頻率要選只有m判定的頻率，結果就是m判定的區間了。結果出來後可以看到，平均值在47-50之間，之前的一個水帖裡我評價過這個判定的體感區間就在±50ms這樣，所以這麼看起來我估的還蠻準的？
但也僅僅是體感區間準而已。現在我必須告訴你們，這個結果一定偏大。至於為什麼，因為一首歌不是全程同一個難度範圍，有簡單的點也有難的點，簡單的段落準度會更多落在中心位置，但我們依然是拿準度偏低的部分來計算，最後結果會使計算出來的絕對σ值偏高，但是我們認為拿這個σ值算出來的區間正好是70ms，因此實際情況是這個我們認為的70ms要比真正的70ms要大才能滿足這種變化。最後結論就是我們算出來的這個判定區間也是偏大的。
已經糊塗了吧？講真我也沒法從數學推論角度證明，我也講的很抽象，我只能告訴你們，其實在捨棄的數據裡還有我打Hydra綠譜的3次成績，拿這個算出來的結果是53左右，可以看出來難度差距越大，算出來的結果也就越大。你們只需要知道這個數字偏大就行了。
其實也沒有大太多，這裡考慮到變化程度，取到±45ms就足夠了，這和網上傳的沒有完全驗證的數據剛好是一樣的。接下來就會把這個結果作為之後計算的依據了，如果之後確定了正確的結果我再修改。
有了這個結果，我們的自動化處理內容就可以繼續了。讓我們看一下這個表格：
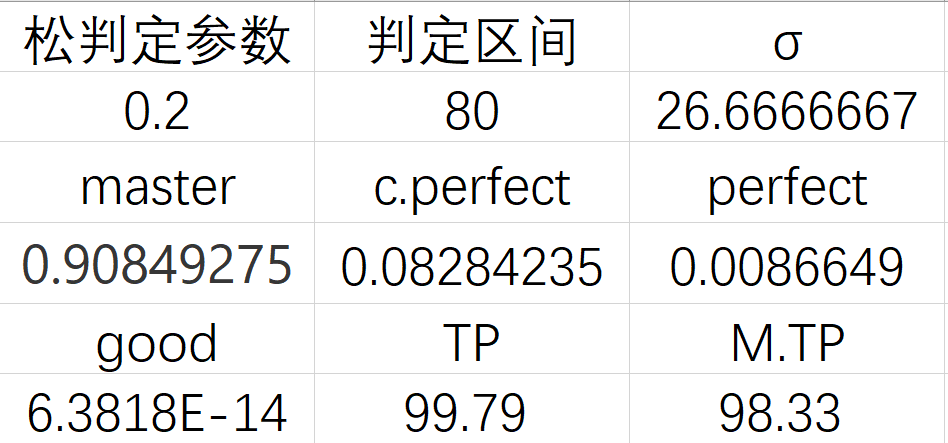松判定參數是上一篇講過的，定義了一定打出最高判定的note比例，不過這個係數也可以增加其他意義，比如菜逼保護啥的，如果只有局部段落準度不穩的話，也可以把打的準的部分算進來，所以這是一個非常靈活調整且完全可以提高一點的參數。在這一次的話紅譜及以下的難度，我取的是0.3，而紫譜及以上的難度我取的是0.2。這個數值也依然是一個相對保守的估計，我看了一下，大部分的歌（主要是統計紫譜）的松判定note的比例會比0.2高，所以如果想取的更精確的結果可以自己單獨數這個譜裡松判定note的佔比，並調整這個參數。當然別取太離譜了，就算是Hydra綠譜這種也最多佔一半，取到0.5基本上是極限了。
而判定區間是我們自己輸入的，這個可以改成很多的數值，除以3就是使用的正態分佈計算時的σ值，在這個基礎上以0為平均值，以對應判定的區間作為終點計算出統計學上的概率比例，用這個比例再加上對應TP/M.TP的權重，當然別忘了松判定參數，最後就可以自動得到TP值和M.TP值了。依然是以5ms為間隔，提供一個新的懶人查詢表：
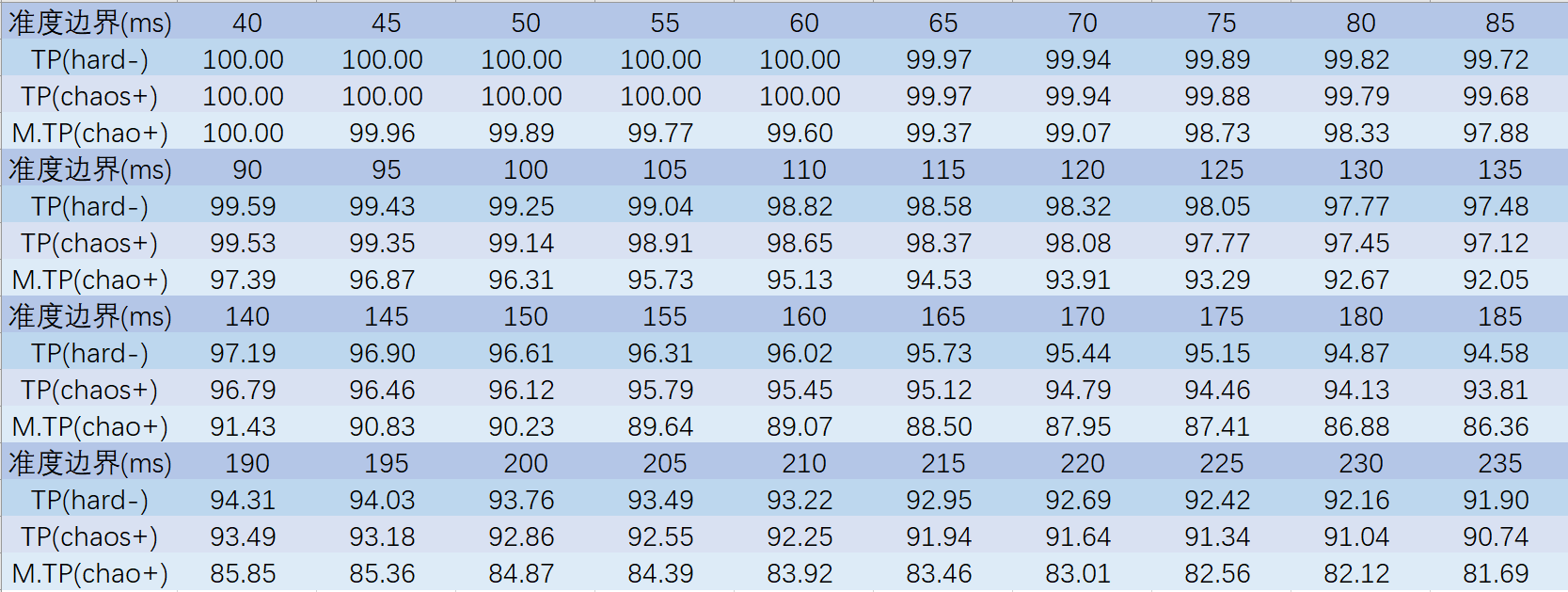用法和上次是一樣的，你打了多少成績，把miss和bad的TP補上，然後找離這個數最近的TP值，查表就可以得到你的準度大概區間是多大了。只不過，在引入嚴判模式的新內容後，我們是不是可以得到一些新的東西了呢？比如，我認為從這個表裡得到的一個最重要的結論就是：在嚴判模式下M.TP達到99.60之後，就可以認為自己在正常模式下達到了理論TP100的成績了。可能大部分人都沒經歷過僅僅爆了一個小p性歌而破防的情況，那退而求其次，僅僅差一個good就MM的經歷總可以了吧，其實也就比這個嚴重那麼幾倍吧。利用嚴判標準，我們可以接受自己在一把裡僅僅爆一兩個小p，只要其他地方的準度更加精確是可以彌補的（打到這種階段基本都是隨機誤差了）。如果你覺得你打的歌鎖鏈多的話可以把這個標準提高，最高到99.75一定夠用了。
其次我們還可以看出來，越遠離絕對完美的準度範圍，M.TP波動的幅度比TP波動大得多，這種趨勢在TP99以上的情況下才明顯，所以能達到這個水平的話用M.TP更加能說明水平。比如大家所認為的TP98算會打，這個情況下M.TP已經跌到94不到了，這和新的權重比例有關，cp只有80%的權重，p僅僅只有一半的權重，必須要為自己的糊歌付出一點代價。啥你問good啊？已經只有一成的權重啦，跟斷了沒啥差別了，之前的那一篇都說了，爆good基本是不能允許的，給你算上都算仁慈了。
那萬一，我打的歌的成績不在這個表裡有對應數字，我還想知道更準確的結果，能做到嗎？
這看起來就是我事先不知道判定範圍的結果，僅僅知道我們剛剛一步步利用公式得到的最終結果TP值，反過來推導最初的參數一樣。沒錯，很像解方程。那麼，Excel能解方程嗎？
還真的可以。
還是剛才那個輸入判定區間輸出TP的表格，這回找到菜單欄的數據→預測→模擬分析→單變量求解的選項：
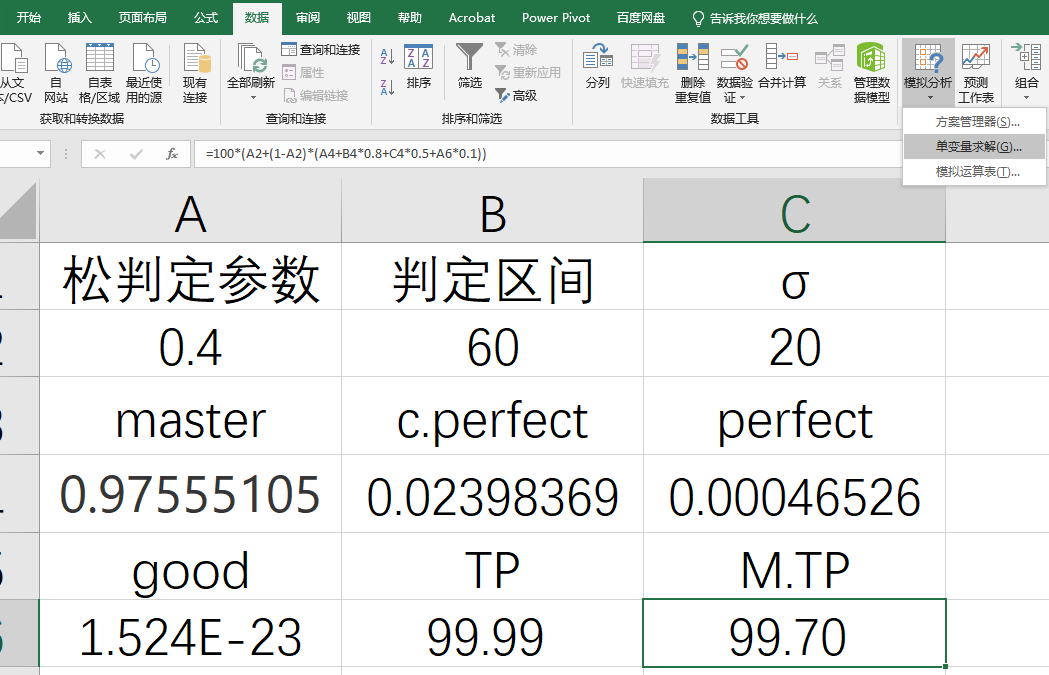目標格選擇你要使用的代表TP的格子，目標值就是你已知的TP值，而可變單元格就是判定區間的格子：
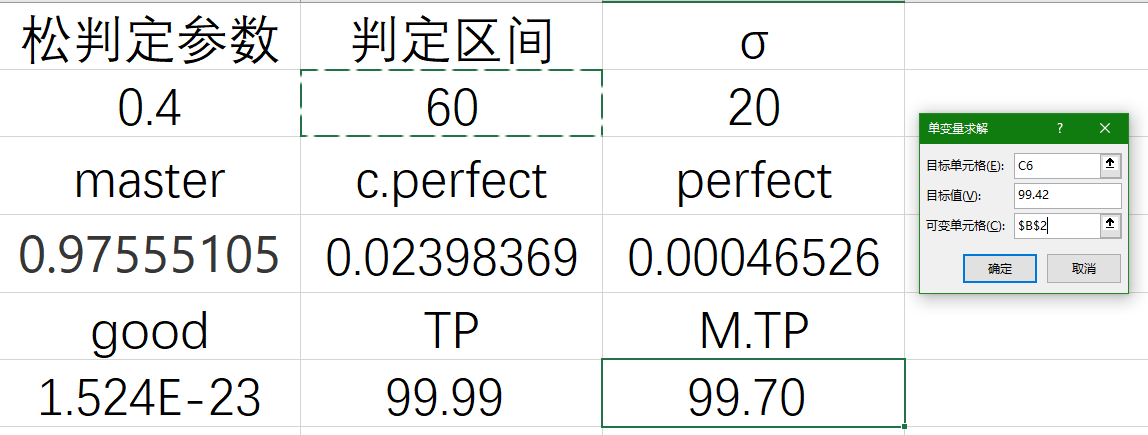點擊確定之後，只要經過幾次迭代之後，就可以得到你的更精準的打歌準度區間了。
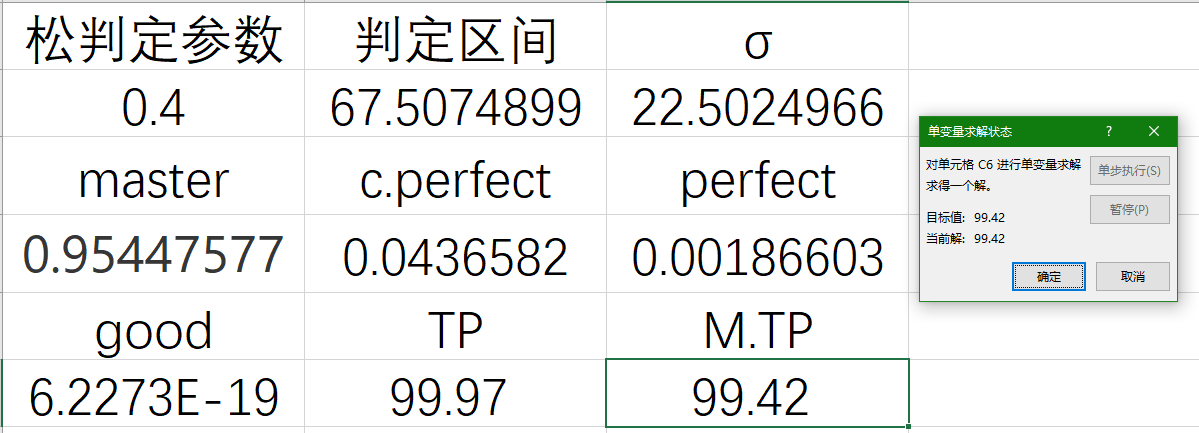當然，松判定參數可以自由改，你可以根據譜面裡一定是最高判定的note比例，或是譜面的難度分配程度進行變動。這個演示是我用我前面打巧克力導彈綠譜的最好成績來帶入的，也可以看到這個水平下的TP值為99.97，正好是一個小p的成績，沒錯我現在也還是一個小的水平（丟臉了……）。這樣看來這個還蠻還原真實水平的。最後，我們還能幹什麼？
除了更嚴格的判定標準之外，嚴判模式還有另一個新增的內容：顯示打擊時刻是快了還是慢了。不過快慢這個詞在音遊裡有太多的地方可以套用了，在打擊時刻上我更傾向於說成早和晚。我們先明確一個大前提：雖然以正確的打擊時刻作為標準考慮，比這個時刻提前打叫早，比這個時刻延後打叫晚，但是如果以你聽到的音樂節奏的時刻作為標準考慮（也就是按照音押標準打），正確打擊時刻偏後叫早，正確打擊時刻偏前叫晚。而這個遊戲的延遲調整並不能改變打擊的note的正確判定的中心位置，只能改變音樂的時間，具體的說就是把延遲的數值調大音樂會更前，反之則會更後。這麼說明只是想要得到一個更直觀的結論：如果打歌結果顯示“早”的數量更多，就說明音樂偏早了，你要反過來降低延遲值；反過來如果結果顯示“晚”的數量更多，就說明音樂偏晚了，你要反過來提高延遲值。
好像說了這麼多真的只有剛才那句是有用的。不過這麼調有用的前提是你得按照音樂打而不是看著note打，純目押的話不管怎麼調延遲，快慢的數據也不會有多少波動。
可能你們已經猜到了，最後我想要做的內容就是：根據嚴判模式打歌結果最後顯示的fast/slow數據，得到應該進行的延遲調整的數值。
然後想想怎麼實現吧，如果是按照先入為主的想法，我一開始打歌的正態分佈結果的平均值已經不是0了，在這種情況下已知兩個絕對數值分別為45ms和-45ms的累計概率分佈，真的可以算出來這個偏差的μ值呢？再退一步講，我怎麼知道這種情況下的σ值？Excel的正態分佈函數的其中兩個參數一個要求另一個根本不知道是多少，難道我要解二元方程？
這其實陷入了一個很大的思維誤區，其實根本不需要解二元方程，我來說明一下怎麼解決這兩個問題。首先，雖然在上面的思路里，要求的兩個累計概率分佈的位置互為相反數，且μ值不是0，這樣第一個平均值的參數本身就帶入了一個未知數的狀態，我們換一個角度想，你的打歌時間的平均值是0，而完美的判定時間並不是±45ms，而是稍微平移了一段時間，比如-35~+55ms，是不是也可以得到一大一小的早晚數據？我們求得這個對應的兩個概率的x值，取個平均數，不就是變相的得到了在兩個概率的x值是±45ms下偏差的μ值嗎？其次，就算絕對的σ值我們不可能從一開始就知道，那也根本不重要，還記得我之前說的嗎？我們完全不需要關心正態分佈的絕對σ值究竟是多少，只需要關心要求的累計概率的絕對位置與σ的比值，也就是相對σ值即可。想想我們根據上一句的算法得到的兩個x值，分別說他是x1和x2（x1<x2）好了。求得的偏差值μ=（x1+x2）/2，而這倆之間的絕對時間間隔=x2-x1，這倆一除，σ就約掉了！所以就算我們再次把公式裡的這個參數設為1，也可以在最後結果把這個參數約掉，而我們已經清楚這個絕對時間間隔=90ms。剩下的事情就簡單了，最後的計算表格就是這個：
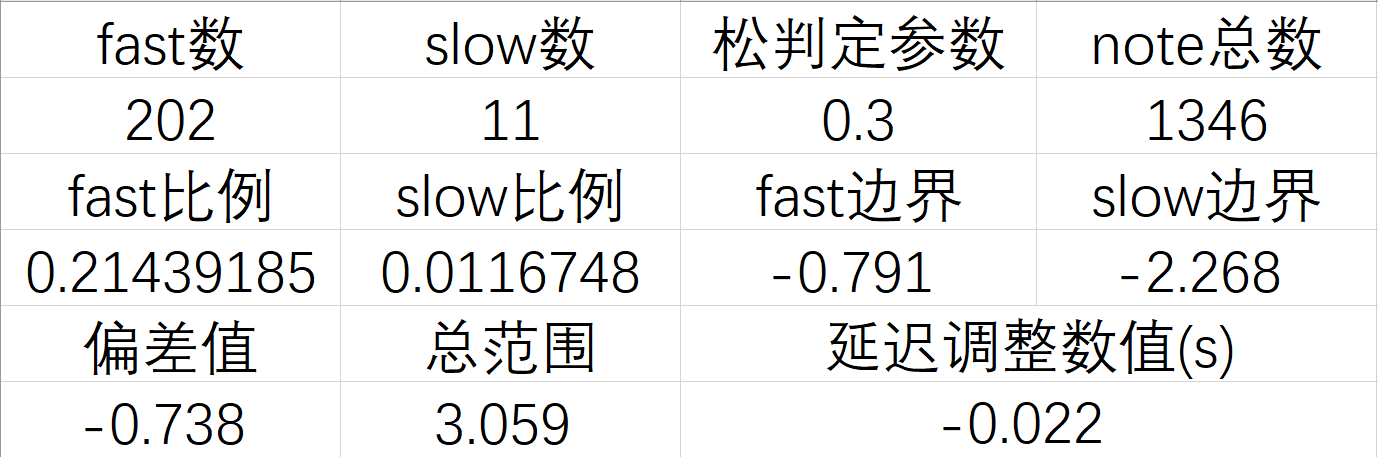第一行四個數是你要輸入的數，當然最後的note總數最好減掉miss的個數，最後的結果就是你需要在現在這個基礎上改變的延遲數值，單位是s，與遊戲裡的一致。你要問我這個真的準嗎？我的回答是：真的不太準。如果是真的想要靠譜一點的結果的話，最後的數值建議再乘個2~2.5，比如上面的數據實際是我在我認為正確的延遲基礎上+0.05s之後，按照我所認為的音押標準打的公交車的成績。另外，如果你的早晚note的數據差如果只有三十幾以下的話，我的建議是調了也沒用，因為在大多數情況下，你打的早還是晚的分佈跟隨機性完全沒有關係，更多跟對鍵型的熟悉程度和note密度有關，不熟悉的段落就是容易打的快一丟丟，而note密度太大的段落就是容易打的偏慢，也就是快慢是存在規律性的，這種情況下用統計學分佈的正態分佈算肯定不太準。這個模式顯示快慢的意義更多在於提醒自己在哪些段落有普遍性的打快打慢，然後自己主動改變打歌的時刻，可能還靠譜一點。
所以這個真的能作為延遲調整的指導嗎？可能吧，大概吧，我覺得有點用吧，前提是乘個2~2.5才準。如果還是對延遲調整一頭霧水的話，不如先從理解“正確的時刻和正確的打擊相對應”開始？或者說如果你看不出來自己認為的聲音是不是在掃描線到圓圈中心才出現的話，我來提供一個一般人不知道的小技巧？
在調整延遲的界面裡，不需要去看第一拍的時刻是不是和掃描線到達圓圈中心的時刻是一致的，而是去看第三拍的時刻是不是正好與掃描線從右邊消失並從左邊出現的瞬間的時刻是一致的。
最後把我上面提到的我製作的Excel文件放到這裡吧。這篇寫了5600多字，希望能夠有人能用得到吧。