那么，本次依然用如星光般璀璨的啦噗哩镇楼。
这次，我们还能做什么呢？我们回到正态分布本身吧。这是一个非常和谐的概率分布函数，当然也是一个运用率很高的函数。在之前的项目中，对于寻找特定准度区间里每种不同判定的统计学分布，我使用了正态分布表，所以对于根据这个得到的σ值再带入表的结果，当然是个估计值，虽然说不会差特别多，但是一个一个对着找也蛮麻烦的。而且这个方法也不可能覆盖更多的准度精度，上次我也仅仅是以5ms为间隔做了一个表。能不能更自动化一点？当然是可以的。总不可能没用过最著名的数据处理软件Excel吧？其中很多人并不一定使用过公式和函数功能，就算用过可能也只是求和平均，再高级一点可能也就算个方差啥的。在Excel里有没有跟正态分布相关的函数？
还真有。隆重请出函数NORM.DIST和NORM.INV。如果你对算数统计啥的看着就想吐，这一段建议别看，后面有懒人包的。对于NORM.DIST函数要输入4个参数，除了最后那个选择是输出累计分布还是概率密度的量（这次我们要用的是前面那个），剩下的只要输入要求的分布的数值x、正态分布的平均数μ以及标准差σ，就可以得到跟正态分布表里一样的结果。就和我上次说的一样，输出的是（-∞，x）的累计概率分布。在我们一开始的假设情况里μ=0，也就是平均准度正好在绝对正确的时刻，而σ在数值上等于我们之后要算的准度区间的1/3。有这个函数之后只要改变σ的值，把x设为大p的判定范围70ms，就可以得到上次那个表的结果了。
那么既然有这个函数了，能不能反过来根据已有的TP值来得到更精确的准度区间的结果？答案显然是可以的，这个就要用到另一个函数NORM.INV了，但是具体这个函数怎么用，我想先卖个关子，让我们把目光放在另一个话题上。
那就是4.7版本新增加的严格判定（master）模式。
啥你还不知道这是个甚么玩意？长按紫谱难度的圆圈就可以切换到这个模式，一个胶囊解锁一首歌的严判模式。需要注意的是只有紫谱和绿谱才能使用这个模式来打歌。不要再问为什么紫谱打歌要花胶囊了，也不要再问为什么自己打过的歌分数突然没了。（虽然后面那个问题更大的可能是因为被某个黑客骇了……）
上次我还引用了某个九把七鸡五连鸡的主播（还有几天就到一周年纪念了）的名言：分数没有意义，快乐才是真谛。然而在严判模式下，就不是分数没有意义这么简单了，分数直接没有了。取而代之的是一个更高级的TP标准：M.TP，并引入了一个更严格的判定：master，这个判定比之前我们见过的大p（官方说法叫c.perfect）更严格，所以没准会看到神仙说出“爆大p”这种以前想都不敢想的说法。顺便说一句，假如在这个判定下打出全部都是master判定的成绩，除了M.TP的结果必然是100之外，最后结算的评价会从正常的Million Master变成Max Master；不过啊假如连MM都没有的话，那最后的评价只有一个简单的Clear，毕竟已经没有分数了。当然我们完全可以按照之前的玩法把这个新判定标准加入进来，最后转换成M.TP的结果，可是还有一个小小的问题：
Master判定的区间是多少ms？
不知道。至少没有一个非常可信的数据。不过我们可以自力更生，算嘛，反正现在的项目也是一直在算，不差这点功夫。现在只需要做的，就是按照正常的状态去打几遍歌，然后统计判定数据，再用已知的大p/小p分界线为70ms得到σ，最后用这个得到的值重新带回累计概率的公式中，就可以得到我们算出来的m/大p分界线了。
但是选的歌也有一点要求，首先要保证点击note的打击难度相对均衡一点，最好不要出现前半段很简单后半段非常难的部分。然后为了减小随机误差要多次实验，这对于理科生的我来说已经是基操了。最后数据相对好看的是这两首：
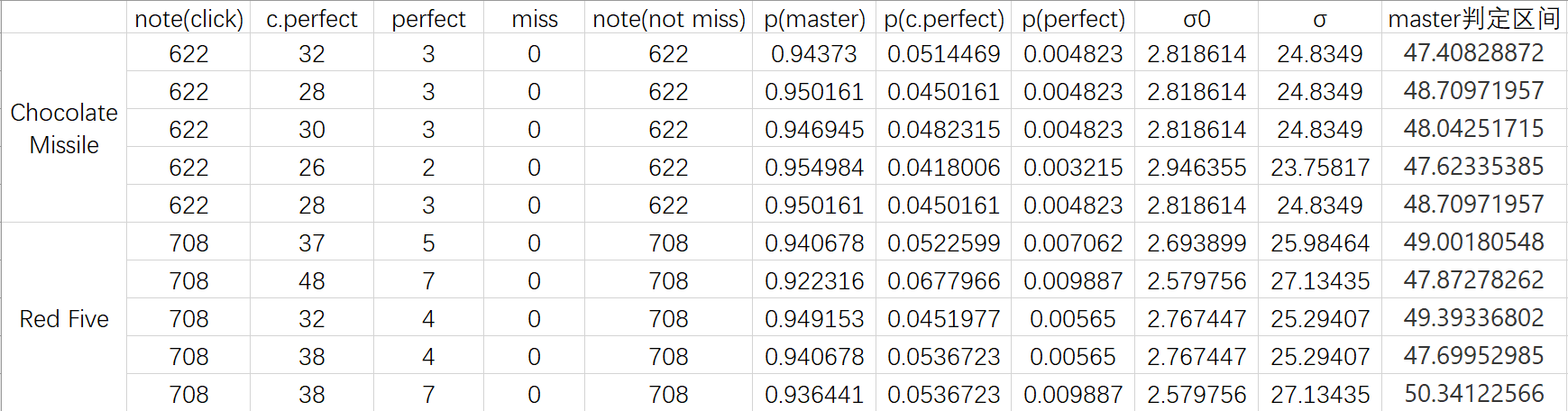巧克力导弹打的是绿谱。解释一下一些列是什么意思，note（click）表示除了只有最高判定的note之外的note总数（点击划键和点锁头），这里不能像上次一样估一个低判定note比例，我需要更精确的比例。σ0是用之前提到过的NORM.INV计算出来的，它和标准公式里的σ意义不一样，因为NORM.INV提供的参数是累计概率p、正态分布的μ和σ，得到的结果是在这个累计概率下对应的正态分布的数值x。这个概率我们就选大p以上判定的频率，也知道这个位置对应的是70ms的位置的累计概率。但是我们怎么知道在这个位置是70ms的前提下，正确的σ值是多少？接下来的一个思想比较重要，之后也会用到：我们完全不需要关心正态分布的绝对σ值究竟是多少，只需要关心要求的累计概率的绝对位置与σ的比值，也就是相对σ值即可。所以这个参数设成1也没有任何问题，所有正态曲线都是相似的，只要缩放一下就OK了。这样得到的这个二点多的σ0值，我们已经认为这个也就是70ms，接下来就用70除以σ0，就得到了之前提到的正确的σ值，用这个σ值反带回到NORM.INV的参数σ里，得到的结果必然是70。最后用这个值，再用一次NORM.INV函数，这次我们的频率要选只有m判定的频率，结果就是m判定的区间了。结果出来后可以看到，平均值在47-50之间，之前的一个水帖里我评价过这个判定的体感区间就在±50ms这样，所以这么看起来我估的还蛮准的？
但也仅仅是体感区间准而已。现在我必须告诉你们，这个结果一定偏大。至于为什么，因为一首歌不是全程同一个难度范围，有简单的点也有难的点，简单的段落准度会更多落在中心位置，但我们依然是拿准度偏低的部分来计算，最后结果会使计算出来的绝对σ值偏高，但是我们认为拿这个σ值算出来的区间正好是70ms，因此实际情况是这个我们认为的70ms要比真正的70ms要大才能满足这种变化。最后结论就是我们算出来的这个判定区间也是偏大的。
已经糊涂了吧？讲真我也没法从数学推论角度证明，我也讲的很抽象，我只能告诉你们，其实在舍弃的数据里还有我打Hydra绿谱的3次成绩，拿这个算出来的结果是53左右，可以看出来难度差距越大，算出来的结果也就越大。你们只需要知道这个数字偏大就行了。
其实也没有大太多，这里考虑到变化程度，取到±45ms就足够了，这和网上传的没有完全验证的数据刚好是一样的。接下来就会把这个结果作为之后计算的依据了，如果之后确定了正确的结果我再修改。
有了这个结果，我们的自动化处理内容就可以继续了。让我们看一下这个表格：
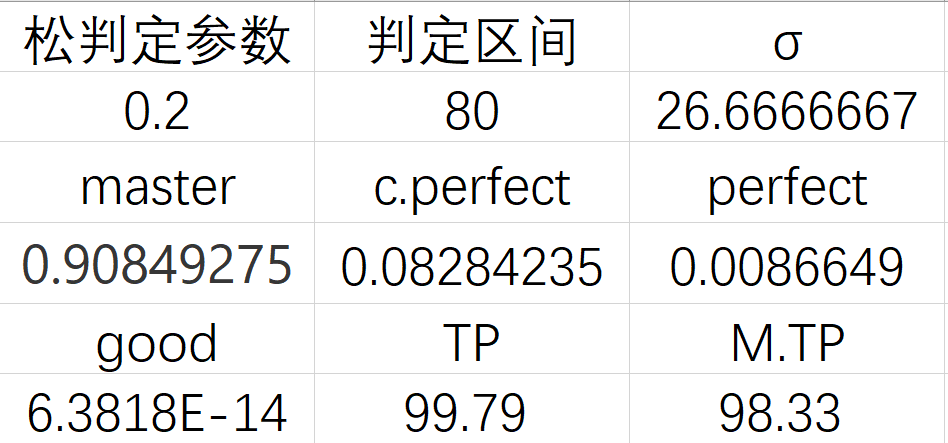松判定参数是上一篇讲过的，定义了一定打出最高判定的note比例，不过这个系数也可以增加其他意义，比如菜逼保护啥的，如果只有局部段落准度不稳的话，也可以把打的准的部分算进来，所以这是一个非常灵活调整且完全可以提高一点的参数。在这一次的话红谱及以下的难度，我取的是0.3，而紫谱及以上的难度我取的是0.2。这个数值也依然是一个相对保守的估计，我看了一下，大部分的歌（主要是统计紫谱）的松判定note的比例会比0.2高，所以如果想取的更精确的结果可以自己单独数这个谱里松判定note的占比，并调整这个参数。当然别取太离谱了，就算是Hydra绿谱这种也最多占一半，取到0.5基本上是极限了。
而判定区间是我们自己输入的，这个可以改成很多的数值，除以3就是使用的正态分布计算时的σ值，在这个基础上以0为平均值，以对应判定的区间作为终点计算出统计学上的概率比例，用这个比例再加上对应TP/M.TP的权重，当然别忘了松判定参数，最后就可以自动得到TP值和M.TP值了。依然是以5ms为间隔，提供一个新的懒人查询表：
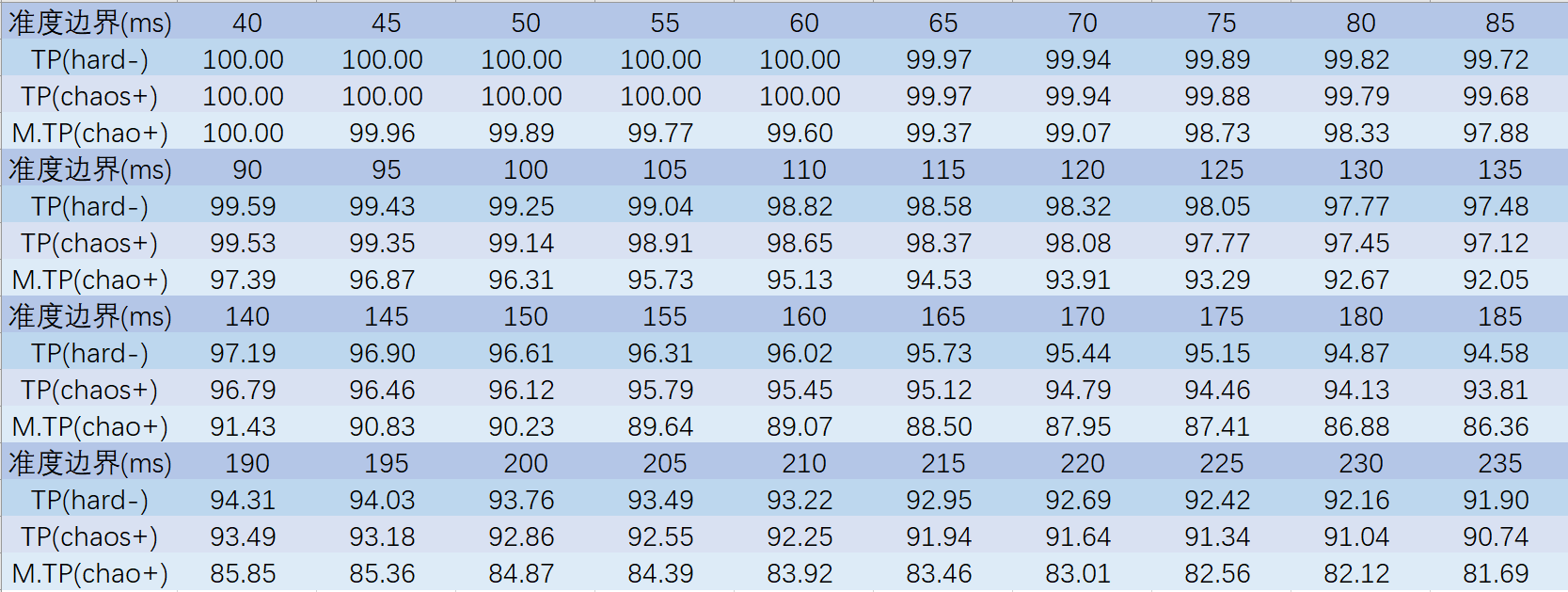用法和上次是一样的，你打了多少成绩，把miss和bad的TP补上，然后找离这个数最近的TP值，查表就可以得到你的准度大概区间是多大了。只不过，在引入严判模式的新内容后，我们是不是可以得到一些新的东西了呢？比如，我认为从这个表里得到的一个最重要的结论就是：在严判模式下M.TP达到99.60之后，就可以认为自己在正常模式下达到了理论TP100的成绩了。可能大部分人都没经历过仅仅爆了一个小p性歌而破防的情况，那退而求其次，仅仅差一个good就MM的经历总可以了吧，其实也就比这个严重那么几倍吧。利用严判标准，我们可以接受自己在一把里仅仅爆一两个小p，只要其他地方的准度更加精确是可以弥补的（打到这种阶段基本都是随机误差了）。如果你觉得你打的歌锁链多的话可以把这个标准提高，最高到99.75一定够用了。
其次我们还可以看出来，越远离绝对完美的准度范围，M.TP波动的幅度比TP波动大得多，这种趋势在TP99以上的情况下才明显，所以能达到这个水平的话用M.TP更加能说明水平。比如大家所认为的TP98算会打，这个情况下M.TP已经跌到94不到了，这和新的权重比例有关，cp只有80%的权重，p仅仅只有一半的权重，必须要为自己的糊歌付出一点代价。啥你问good啊？已经只有一成的权重啦，跟断了没啥差别了，之前的那一篇都说了，爆good基本是不能允许的，给你算上都算仁慈了。
那万一，我打的歌的成绩不在这个表里有对应数字，我还想知道更准确的结果，能做到吗？
这看起来就是我事先不知道判定范围的结果，仅仅知道我们刚刚一步步利用公式得到的最终结果TP值，反过来推导最初的参数一样。没错，很像解方程。那么，Excel能解方程吗？
还真的可以。
还是刚才那个输入判定区间输出TP的表格，这回找到菜单栏的数据→预测→模拟分析→单变量求解的选项：
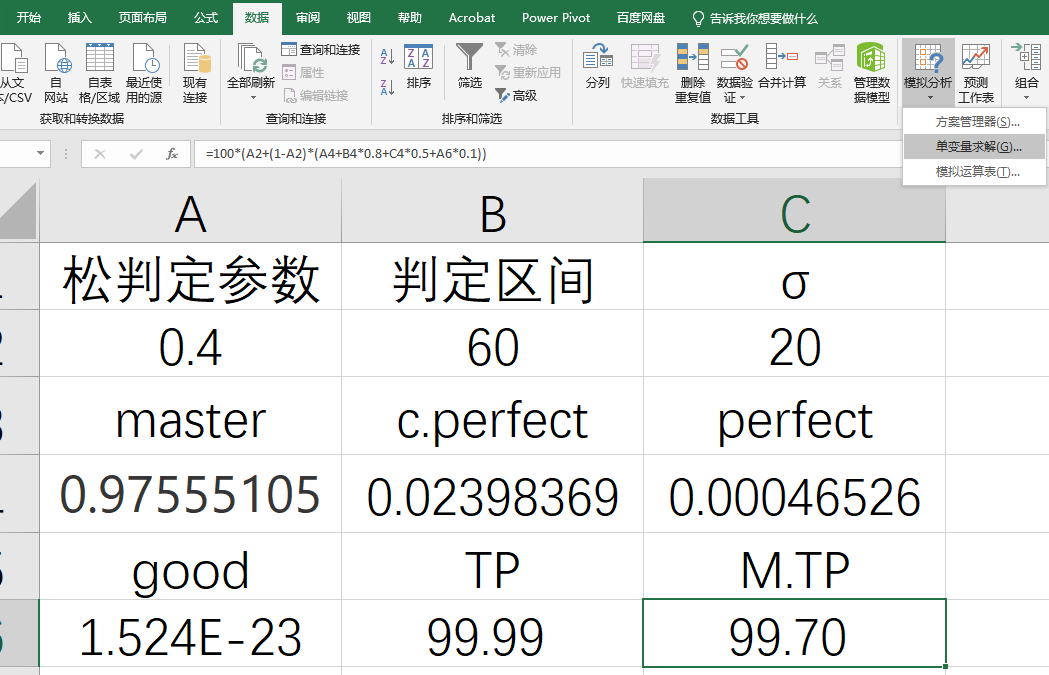目标格选择你要使用的代表TP的格子，目标值就是你已知的TP值，而可变单元格就是判定区间的格子：
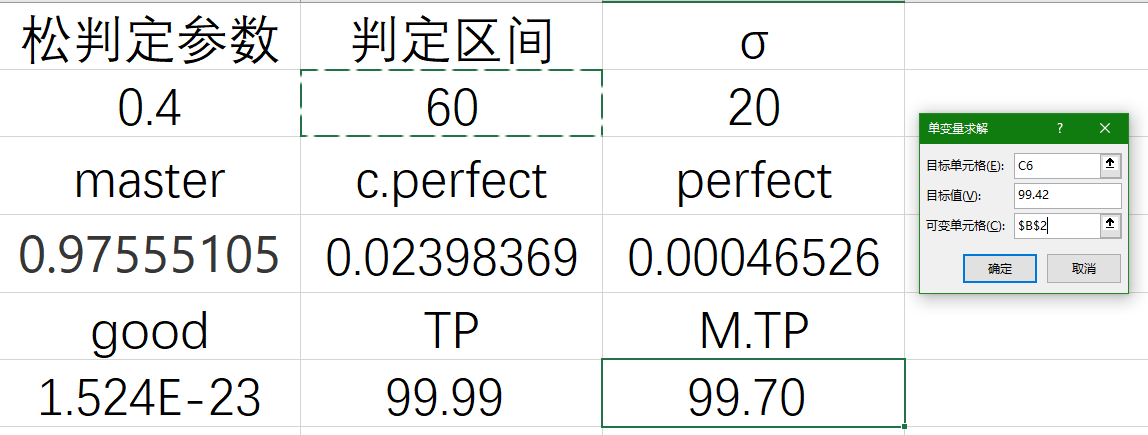点击确定之后，只要经过几次迭代之后，就可以得到你的更精准的打歌准度区间了。
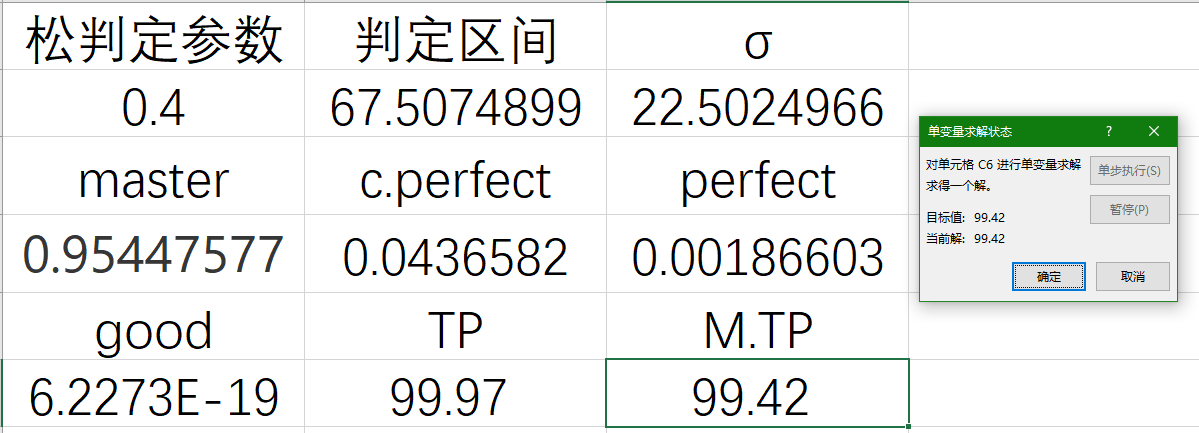当然，松判定参数可以自由改，你可以根据谱面里一定是最高判定的note比例，或是谱面的难度分配程度进行变动。这个演示是我用我前面打巧克力导弹绿谱的最好成绩来带入的，也可以看到这个水平下的TP值为99.97，正好是一个小p的成绩，没错我现在也还是一个小的水平（丢脸了……）。这样看来这个还蛮还原真实水平的。最后，我们还能干什么？
除了更严格的判定标准之外，严判模式还有另一个新增的内容：显示打击时刻是快了还是慢了。不过快慢这个词在音游里有太多的地方可以套用了，在打击时刻上我更倾向于说成早和晚。我们先明确一个大前提：虽然以正确的打击时刻作为标准考虑，比这个时刻提前打叫早，比这个时刻延后打叫晚，但是如果以你听到的音乐节奏的时刻作为标准考虑（也就是按照音押标准打），正确打击时刻偏后叫早，正确打击时刻偏前叫晚。而这个游戏的延迟调整并不能改变打击的note的正确判定的中心位置，只能改变音乐的时间，具体的说就是把延迟的数值调大音乐会更前，反之则会更后。这么说明只是想要得到一个更直观的结论：如果打歌结果显示“早”的数量更多，就说明音乐偏早了，你要反过来降低延迟值；反过来如果结果显示“晚”的数量更多，就说明音乐偏晚了，你要反过来提高延迟值。
好像说了这么多真的只有刚才那句是有用的。不过这么调有用的前提是你得按照音乐打而不是看着note打，纯目押的话不管怎么调延迟，快慢的数据也不会有多少波动。
可能你们已经猜到了，最后我想要做的内容就是：根据严判模式打歌结果最后显示的fast/slow数据，得到应该进行的延迟调整的数值。
然后想想怎么实现吧，如果是按照先入为主的想法，我一开始打歌的正态分布结果的平均值已经不是0了，在这种情况下已知两个绝对数值分别为45ms和-45ms的累计概率分布，真的可以算出来这个偏差的μ值呢？再退一步讲，我怎么知道这种情况下的σ值？Excel的正态分布函数的其中两个参数一个要求另一个根本不知道是多少，难道我要解二元方程？
这其实陷入了一个很大的思维误区，其实根本不需要解二元方程，我来说明一下怎么解决这两个问题。首先，虽然在上面的思路里，要求的两个累计概率分布的位置互为相反数，且μ值不是0，这样第一个平均值的参数本身就带入了一个未知数的状态，我们换一个角度想，你的打歌时间的平均值是0，而完美的判定时间并不是±45ms，而是稍微平移了一段时间，比如-35~+55ms，是不是也可以得到一大一小的早晚数据？我们求得这个对应的两个概率的x值，取个平均数，不就是变相的得到了在两个概率的x值是±45ms下偏差的μ值吗？其次，就算绝对的σ值我们不可能从一开始就知道，那也根本不重要，还记得我之前说的吗？我们完全不需要关心正态分布的绝对σ值究竟是多少，只需要关心要求的累计概率的绝对位置与σ的比值，也就是相对σ值即可。想想我们根据上一句的算法得到的两个x值，分别说他是x1和x2（x1<x2）好了。求得的偏差值μ=（x1+x2）/2，而这俩之间的绝对时间间隔=x2-x1，这俩一除，σ就约掉了！所以就算我们再次把公式里的这个参数设为1，也可以在最后结果把这个参数约掉，而我们已经清楚这个绝对时间间隔=90ms。剩下的事情就简单了，最后的计算表格就是这个：
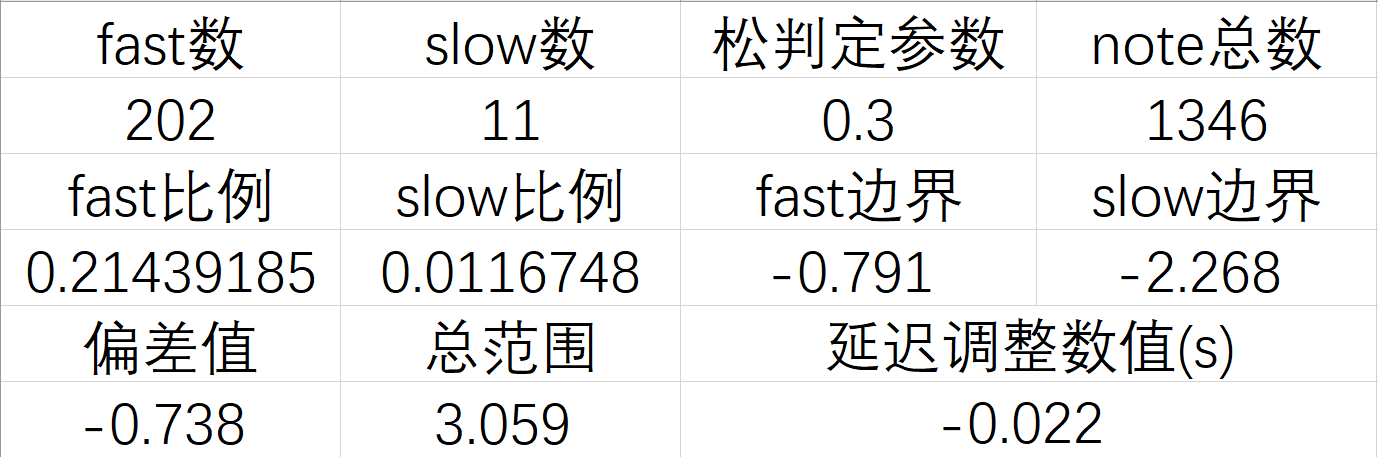第一行四个数是你要输入的数，当然最后的note总数最好减掉miss的个数，最后的结果就是你需要在现在这个基础上改变的延迟数值，单位是s，与游戏里的一致。你要问我这个真的准吗？我的回答是：真的不太准。如果是真的想要靠谱一点的结果的话，最后的数值建议再乘个2~2.5，比如上面的数据实际是我在我认为正确的延迟基础上+0.05s之后，按照我所认为的音押标准打的公交车的成绩。另外，如果你的早晚note的数据差如果只有三十几以下的话，我的建议是调了也没用，因为在大多数情况下，你打的早还是晚的分布跟随机性完全没有关系，更多跟对键型的熟悉程度和note密度有关，不熟悉的段落就是容易打的快一丢丢，而note密度太大的段落就是容易打的偏慢，也就是快慢是存在规律性的，这种情况下用统计学分布的正态分布算肯定不太准。这个模式显示快慢的意义更多在于提醒自己在哪些段落有普遍性的打快打慢，然后自己主动改变打歌的时刻，可能还靠谱一点。
所以这个真的能作为延迟调整的指导吗？可能吧，大概吧，我觉得有点用吧，前提是乘个2~2.5才准。如果还是对延迟调整一头雾水的话，不如先从理解“正确的时刻和正确的打击相对应”开始？或者说如果你看不出来自己认为的声音是不是在扫描线到圆圈中心才出现的话，我来提供一个一般人不知道的小技巧？
在调整延迟的界面里，不需要去看第一拍的时刻是不是和扫描线到达圆圈中心的时刻是一致的，而是去看第三拍的时刻是不是正好与扫描线从右边消失并从左边出现的瞬间的时刻是一致的。
最后把我上面提到的我制作的Excel文件放到这里吧。这篇写了5600多字，希望能够有人能用得到吧。