本文僅論證在只報出內場三個圖案後(如034),是否能在不溝通的情況下完成交換,以駁斥認為不使用傻瓜式打法就必須溝通的觀點。至於和傻瓜式打法孰優孰劣,動腦程度,不予置評。如有錯誤,敬請指正。
先簡單介紹下內場正常分法:如果自己是兩個一樣的,一人塞一個;如果是不一樣的,先把自己沒有的塞給不需要這個的隊友,再把另一個塞給剩下的隊友。
接下來是驗證過程。
首先,內場報自己雕像手持圖案。由於手持圖案順序不影響分圖形,所以這裡採用034。
由於每個人至少持有一個自己的圖形,所以三個房間依次各有一個0,一個3和一個4,接下來將剩餘的三個圖形隨機分配,共有如下6種情況:
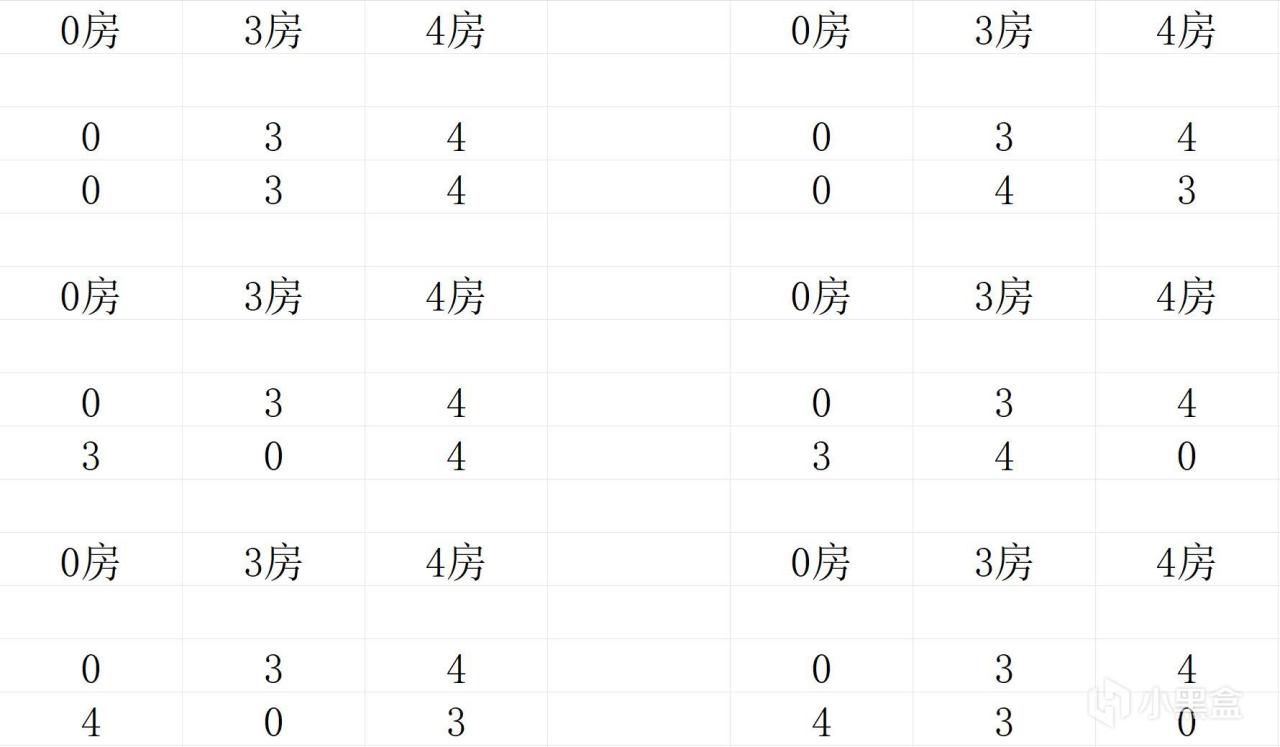
接下來進行分類討論:
情況一:每個人都是自己的兩個圖案
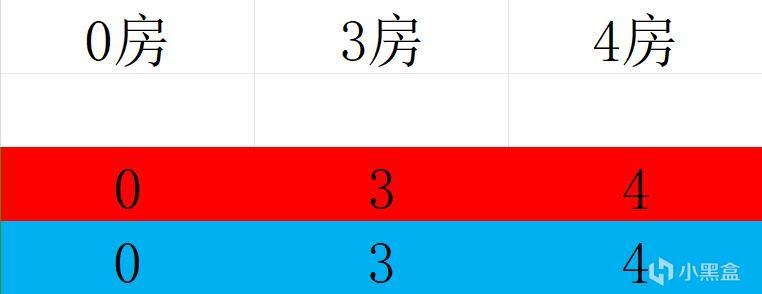
為了方便觀察調換過程,這裡用顏色對每個圖形進行區分,即每個圖形均有紅藍兩個。每個人都有兩個自己的圖案,按照正常分法,每個人都一人給一個,分完後變為黑框中所示:
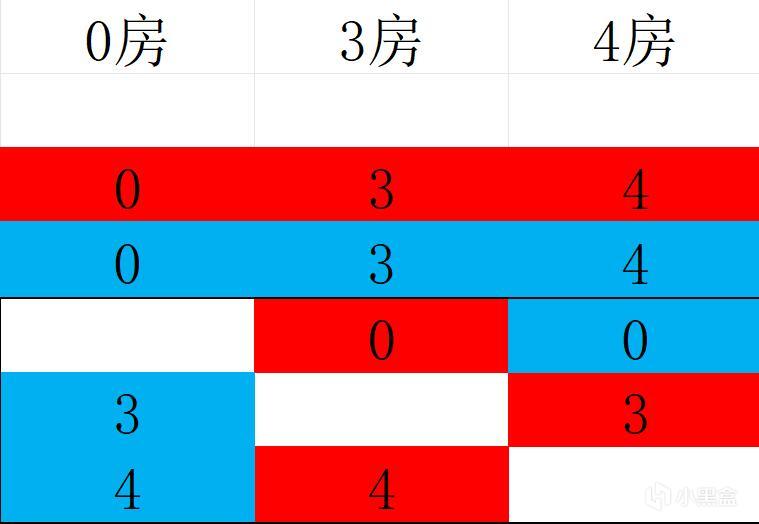
可以看到圖形分配滿足要求,每一步均為1藍1紅,代表來自同一個人所分,總數為3藍3紅,代表沒有無中生圖。
情況二:只有一個人是自己的兩個圖案
這裡以0房持有兩個0舉例。
按照正常打法,0房把兩個0給出去。3房持有3和4,由於隊友是0和4,4房不需要4,因此先將4塞給0房,再將3塞給4房。同理4房將3塞給0房,4塞給3房。圖案變為黑框中所示:
可以看到分配滿足要求。剩下兩種情況同理
情況三:沒有人有相同的圖案
按照分配規則,0房持有03,隊友為3和4,因為3房不需要3,因此將3塞給4房,0塞給3房。同理,3房將4塞給0房,3塞給4房。4房將0塞給3房,4塞給0房。圖案變為黑框中所示:
此時,每人擁有兩個相同的自己需要的圖案,此時將其中一個分給需要的隊友,即:4房不需要4,因此0房將一個4給3房。同理3房將一個0分給4房,4房將一個3分給0房,即可完成分配。
此情況流程同上,省略不表。
總結
綜上所述,在無溝通情況下,可以將內場正確分配。有4種情況可以6次分配完畢,2種情況9次分配完畢,期望分配次數為7次。
下圖為傻瓜式打法每種情況分配數,期望分配數為8次。