本文仅论证在只报出内场三个图案后(如034),是否能在不沟通的情况下完成交换,以驳斥认为不使用傻瓜式打法就必须沟通的观点。至于和傻瓜式打法孰优孰劣,动脑程度,不予置评。如有错误,敬请指正。
先简单介绍下内场正常分法:如果自己是两个一样的,一人塞一个;如果是不一样的,先把自己没有的塞给不需要这个的队友,再把另一个塞给剩下的队友。
接下来是验证过程。
首先,内场报自己雕像手持图案。由于手持图案顺序不影响分图形,所以这里采用034。
由于每个人至少持有一个自己的图形,所以三个房间依次各有一个0,一个3和一个4,接下来将剩余的三个图形随机分配,共有如下6种情况:
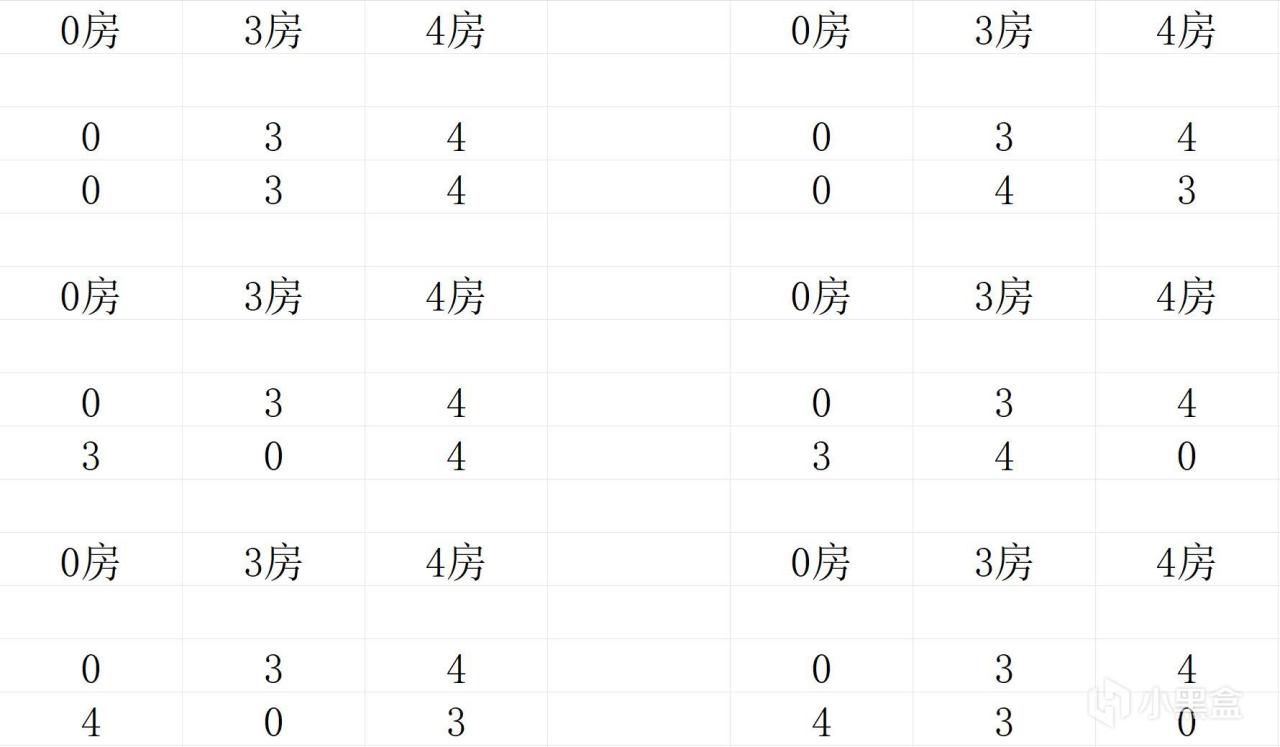
接下来进行分类讨论:
情况一:每个人都是自己的两个图案
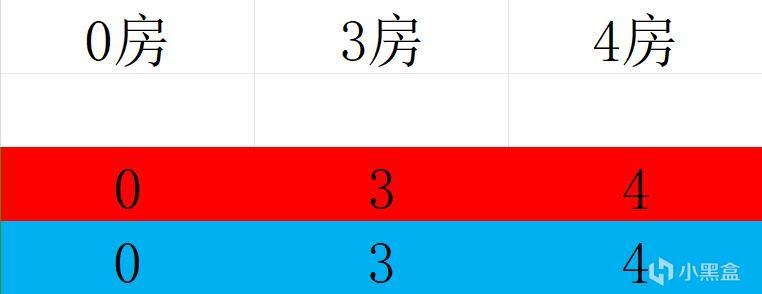
为了方便观察调换过程,这里用颜色对每个图形进行区分,即每个图形均有红蓝两个。每个人都有两个自己的图案,按照正常分法,每个人都一人给一个,分完后变为黑框中所示:
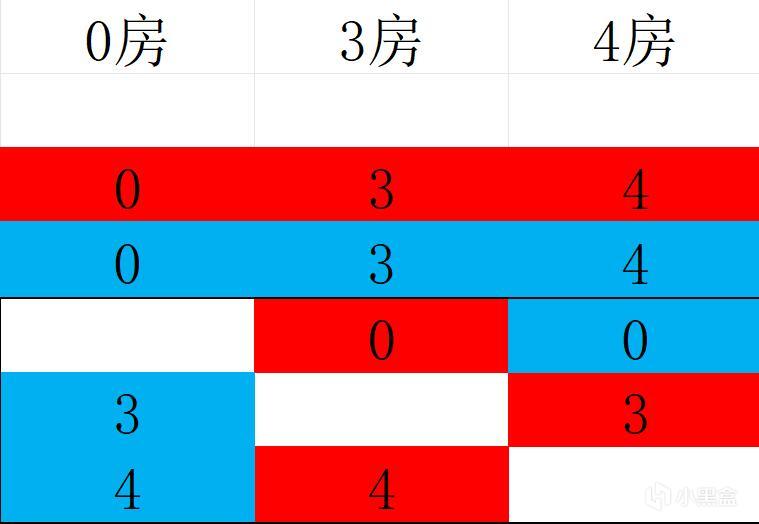
可以看到图形分配满足要求,每一步均为1蓝1红,代表来自同一个人所分,总数为3蓝3红,代表没有无中生图。
情况二:只有一个人是自己的两个图案
这里以0房持有两个0举例。
按照正常打法,0房把两个0给出去。3房持有3和4,由于队友是0和4,4房不需要4,因此先将4塞给0房,再将3塞给4房。同理4房将3塞给0房,4塞给3房。图案变为黑框中所示:
可以看到分配满足要求。剩下两种情况同理
情况三:没有人有相同的图案
按照分配规则,0房持有03,队友为3和4,因为3房不需要3,因此将3塞给4房,0塞给3房。同理,3房将4塞给0房,3塞给4房。4房将0塞给3房,4塞给0房。图案变为黑框中所示:
此时,每人拥有两个相同的自己需要的图案,此时将其中一个分给需要的队友,即:4房不需要4,因此0房将一个4给3房。同理3房将一个0分给4房,4房将一个3分给0房,即可完成分配。
此情况流程同上,省略不表。
总结
综上所述,在无沟通情况下,可以将内场正确分配。有4种情况可以6次分配完毕,2种情况9次分配完毕,期望分配次数为7次。
下图为傻瓜式打法每种情况分配数,期望分配数为8次。