我們先從一個簡單的概念入手,球體追蹤(Sphere Tracing)。
假設有一個二維平面,這個平面上有一個圓和一個正方形,它們彼此並不重疊,同時保持了一定距離。此時有一個點,從該點以某個方向射出一條射線。我們想知道這條射線是否與平面上的那兩個圖形相交。最簡單的做法是,我們讓射線發射,並以某個步長為基準,每次讓射線前進一個步長,每次前進一個步長後,測量射線端點到每個圖形的距離。如果某次測量結果為小於等於0,那麼則可以判定這個射線與這個圖形相交。
但是這個做法有一個致命的缺陷,如果步長選的過大,那麼導致的結果就很可能是射線在某次前進時,直接越過了圖形。這樣我們就得到了一個錯誤的結果。所以不難看出,步長的選擇是關鍵。
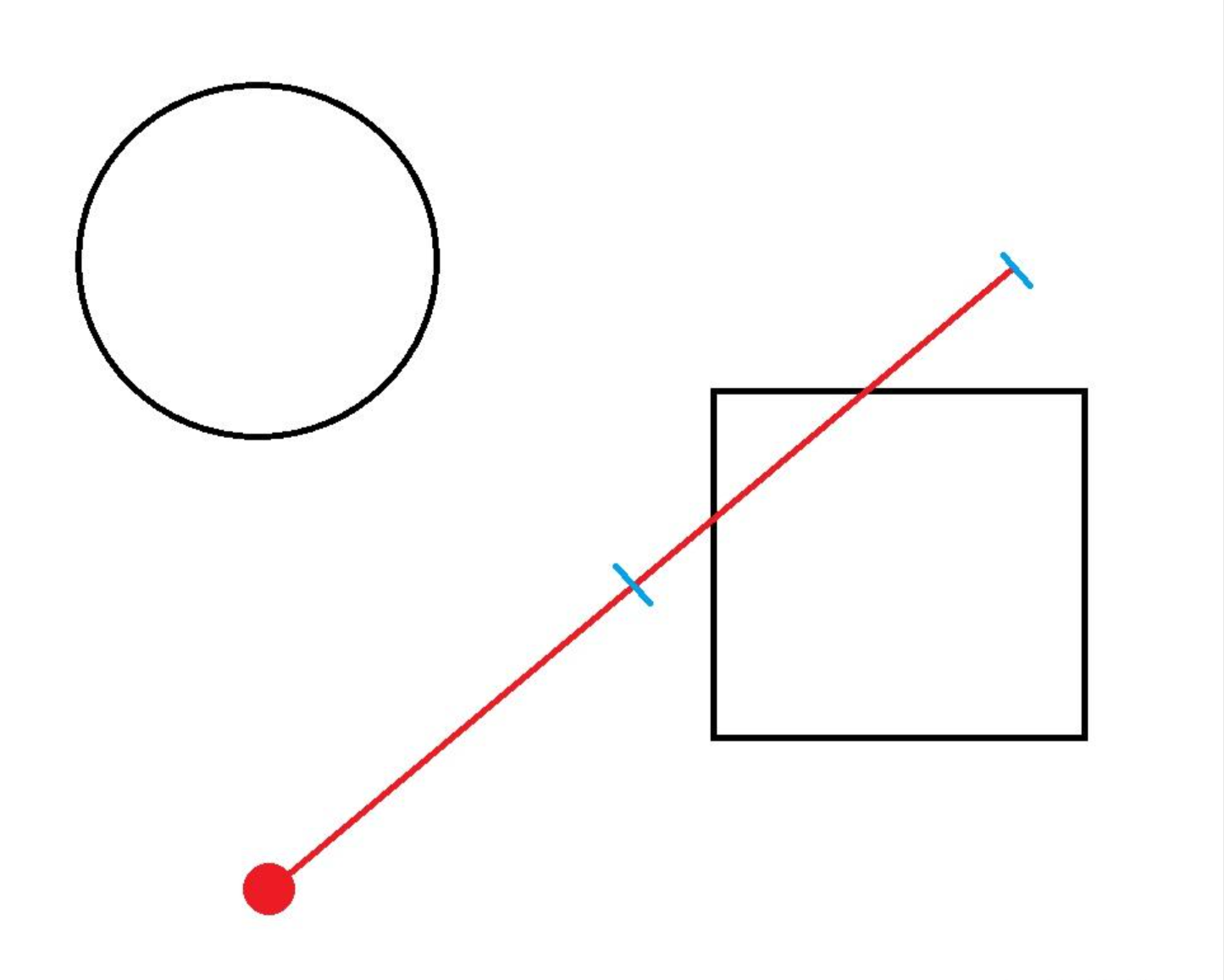
球體追蹤就是為了解決這個問題。
還是同一個平面,存在同樣的兩個圖形,同樣的射線準備發射,此時不同的是,在第一個步長前,我們先測量一次起始點到所有圖形的距離。在得到的所有距離中,我們選擇最短的那個距離,以這個距離為步長,讓射線開始第一次前進。第一次前進結束後,我們測量端點到所有圖形距離,和之前一樣,取最短距離作為下一次前進的步長。
以每次前進後的射線端點為中心,以每次前進的步長為半徑畫圓,觀察後我們發現,射線每次都以與圖形的最短距離為步長前進,除非這個最短距離的方向與射線發射方向一致,否則只要存在任何一點角度偏差,射線也不會擊中任何東西,這也就排除了越過任何圖形的可能。
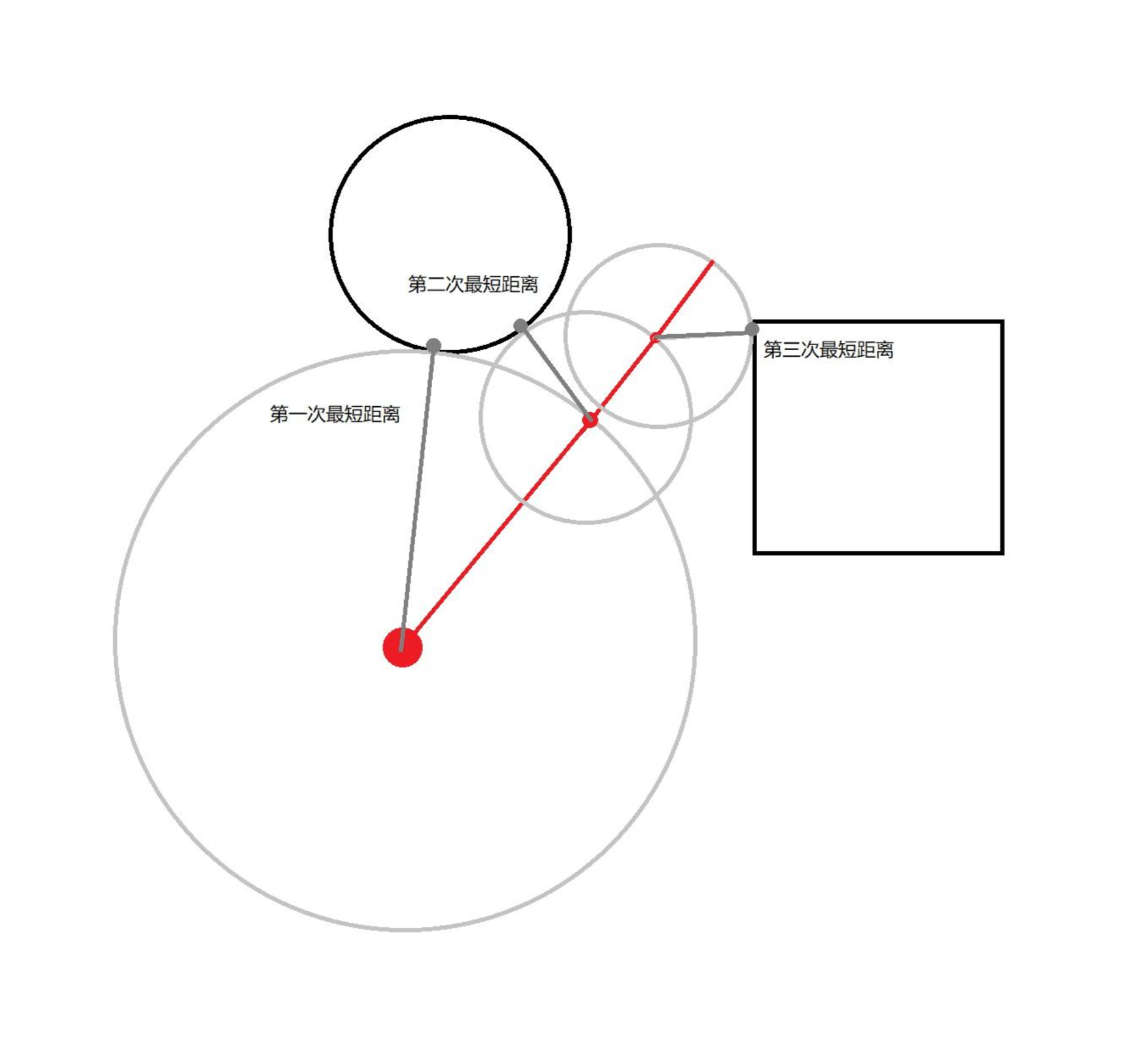
在描述球體追蹤概念時,計算點到圖形的距離是一個非常關鍵的步驟,同時也是一個比較複雜的步驟。那麼如果我們將這個距離提前緩存起來,是不是就減少了球體追蹤算法的複雜度呢?答案是肯定的,這就是網格體距離場(後稱 MDF )所要發揮的作用。
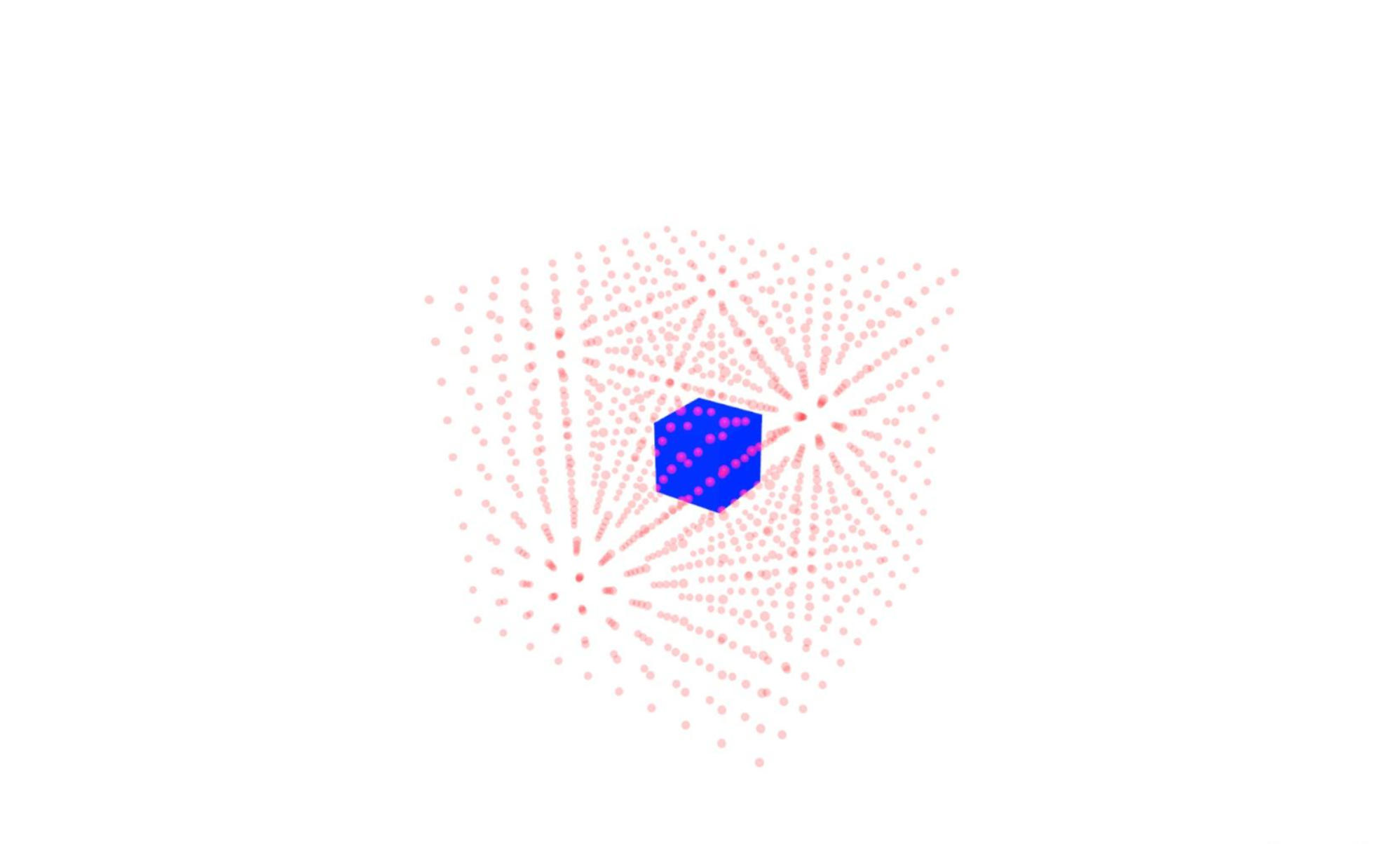
由圖所示,我們在一個空間中,按照一定數量和間距擺放一些小球,然後將我們想要計算 MDF 的網格置入這些小球中(有一部分小球會在網格體內)。接下來我們計算每個小球到達網格體表面的最近距離,網格體內小球距離為負數,網格體外小球距離為正數。這些以小球為採樣點計算得來的,每個採樣點距離網格體的最短距離數據的集合,被稱為網格體距離場的體積紋理(mesh distance field volume texture)。上圖所示中產生的體積紋理大小為 10 x 10 x 10。有了整個體積紋理,在球體追蹤計算時,點到圖形距離就可以直接從這個體積紋理中獲取。
值得一提的是,每個網格的 MDF 是獨立的,它只保存了比網格稍大一些空間內的距離數據(而不是整個場景的,取決於採樣點如何安放),也就是說在實際計算中,從體積紋理中獲取數據時需要場景空間位置到體積紋理取值位置的映射,這個映射數據也包含在網格體距離場中。
虛幻文檔在講解 MDF 時,由於主語不清晰,很容易導致閱讀者以為距離場的計算時在整個場景中進行的,這樣在虛幻引擎將 MDF 可視化後得到的視覺效果會讓閱讀者感到非常疑惑,因為場景中各個網格體之間的距離並沒有影響整個可視化的效果,其實是沒有搞清楚 MDF 的計算主體。
最後再說一下全局距離場(global distance field,GDF)
GDF 是組合相機視野中的每個 MDF,然後計算合併而得來。因為要集合多個 MDF,所以產生的體積紋理分辨率必然會非常低(不然會很大)。通過虛幻引擎中對 GDF 的可視化結果能夠清晰看到低分辨率產生的特點。
圖1,空場景中有兩個正方體
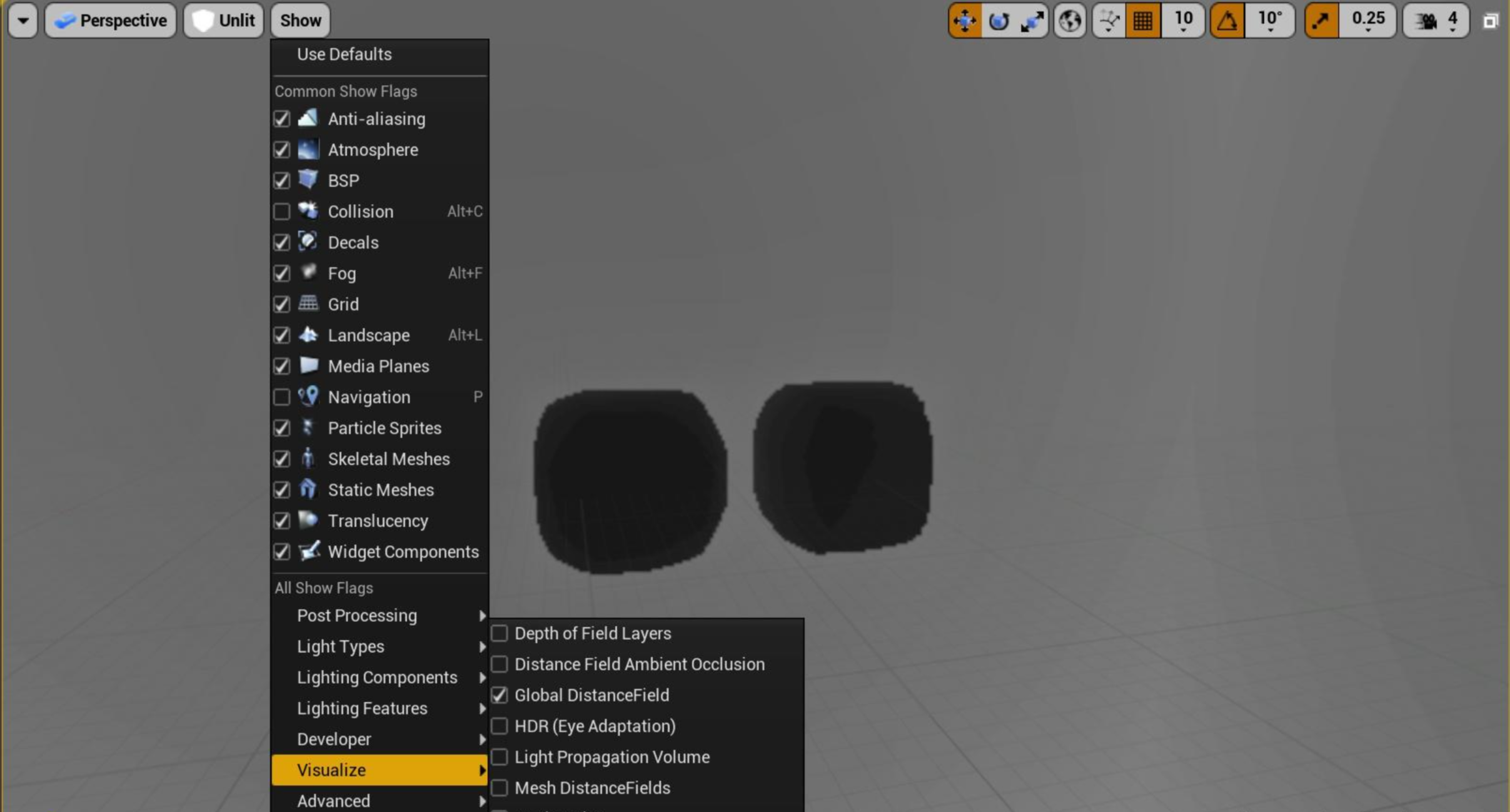
圖2,開啟 GDF 可視化

圖3,讓其中一個正方體稍微靠近另一個,還保有空隙,但 GDF 可視化中兩個正方體中間的縫隙就會被黑色填補