我们先从一个简单的概念入手,球体追踪(Sphere Tracing)。
假设有一个二维平面,这个平面上有一个圆和一个正方形,它们彼此并不重叠,同时保持了一定距离。此时有一个点,从该点以某个方向射出一条射线。我们想知道这条射线是否与平面上的那两个图形相交。最简单的做法是,我们让射线发射,并以某个步长为基准,每次让射线前进一个步长,每次前进一个步长后,测量射线端点到每个图形的距离。如果某次测量结果为小于等于0,那么则可以判定这个射线与这个图形相交。
但是这个做法有一个致命的缺陷,如果步长选的过大,那么导致的结果就很可能是射线在某次前进时,直接越过了图形。这样我们就得到了一个错误的结果。所以不难看出,步长的选择是关键。
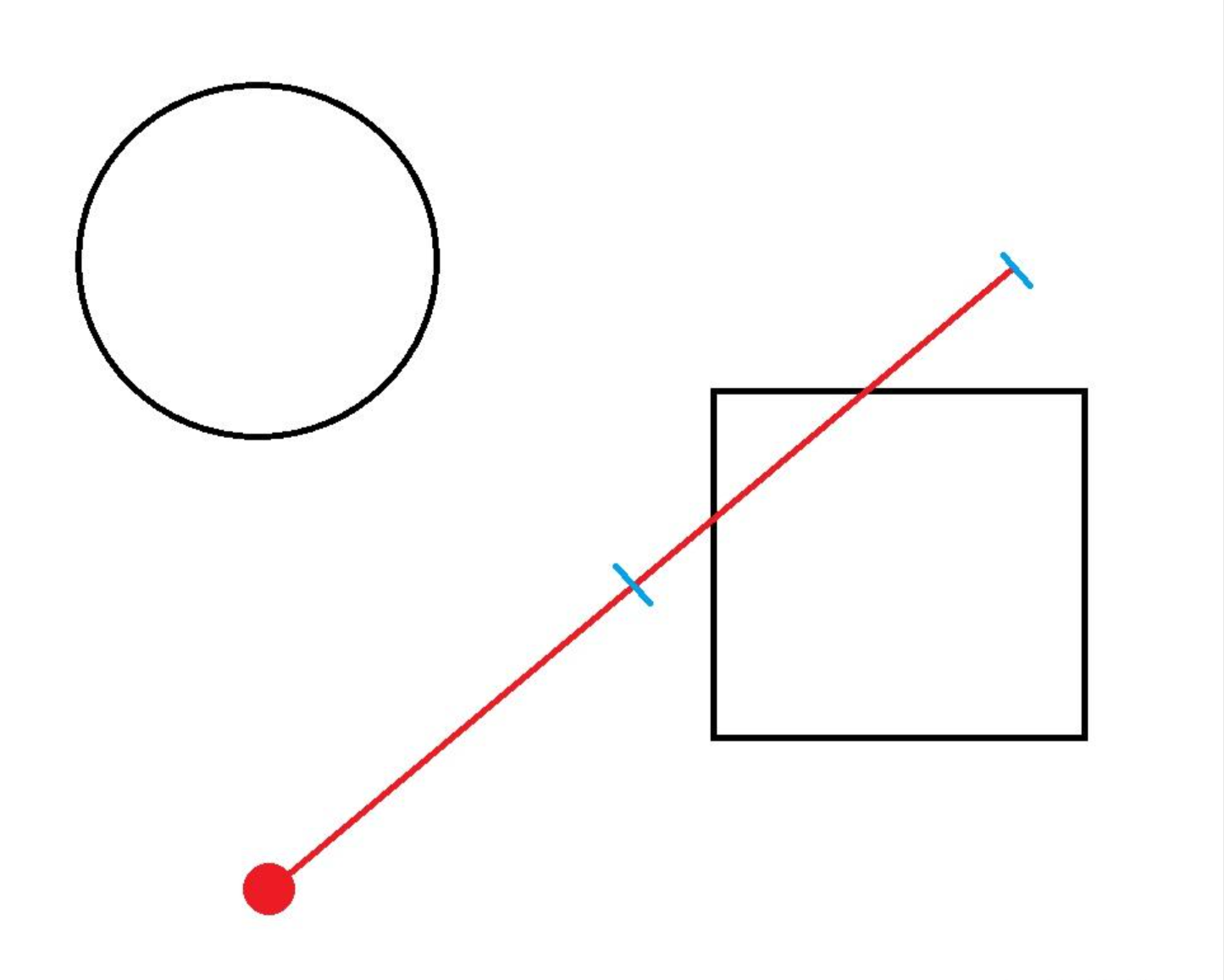
球体追踪就是为了解决这个问题。
还是同一个平面,存在同样的两个图形,同样的射线准备发射,此时不同的是,在第一个步长前,我们先测量一次起始点到所有图形的距离。在得到的所有距离中,我们选择最短的那个距离,以这个距离为步长,让射线开始第一次前进。第一次前进结束后,我们测量端点到所有图形距离,和之前一样,取最短距离作为下一次前进的步长。
以每次前进后的射线端点为中心,以每次前进的步长为半径画圆,观察后我们发现,射线每次都以与图形的最短距离为步长前进,除非这个最短距离的方向与射线发射方向一致,否则只要存在任何一点角度偏差,射线也不会击中任何东西,这也就排除了越过任何图形的可能。
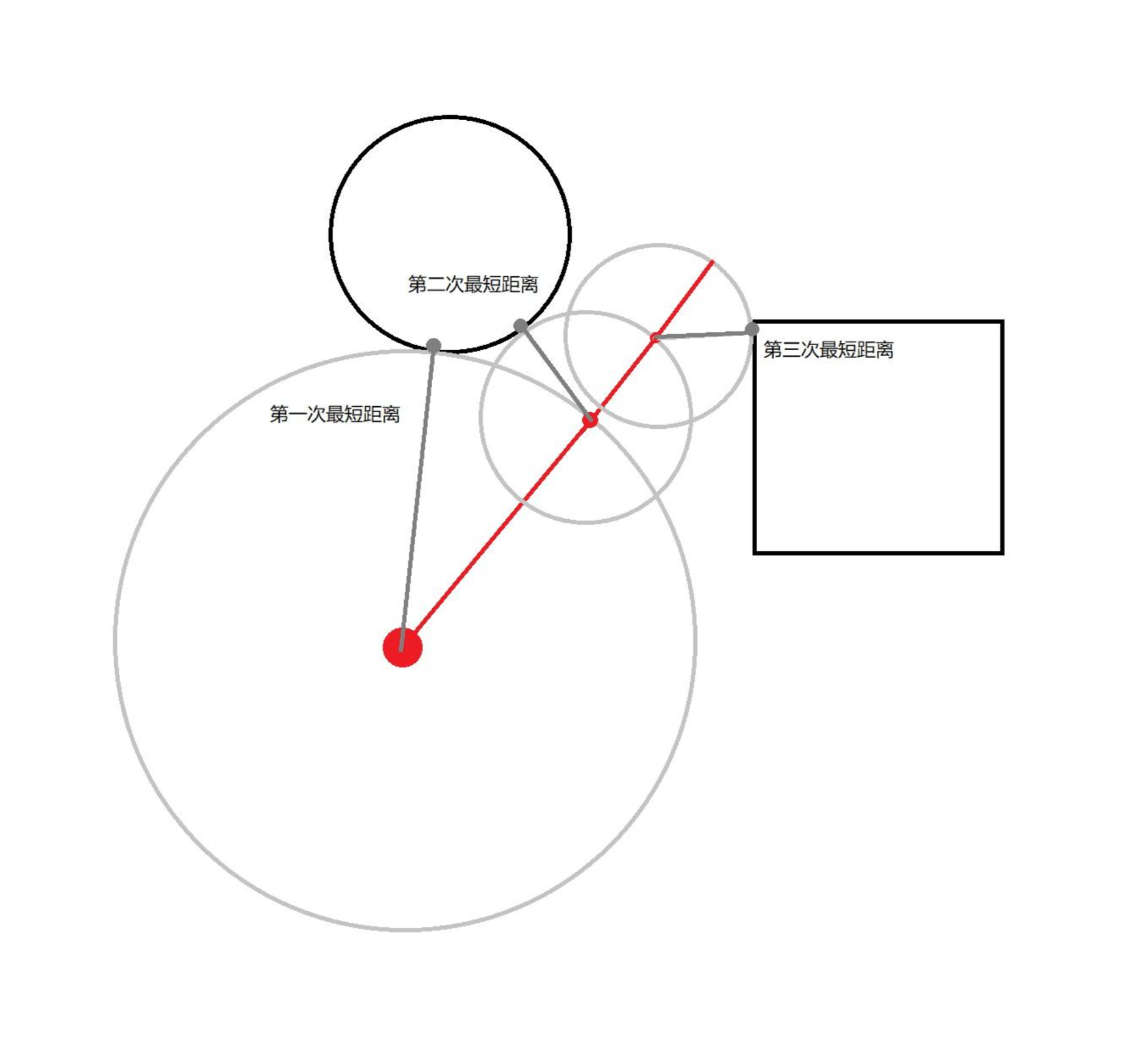
在描述球体追踪概念时,计算点到图形的距离是一个非常关键的步骤,同时也是一个比较复杂的步骤。那么如果我们将这个距离提前缓存起来,是不是就减少了球体追踪算法的复杂度呢?答案是肯定的,这就是网格体距离场(后称 MDF )所要发挥的作用。
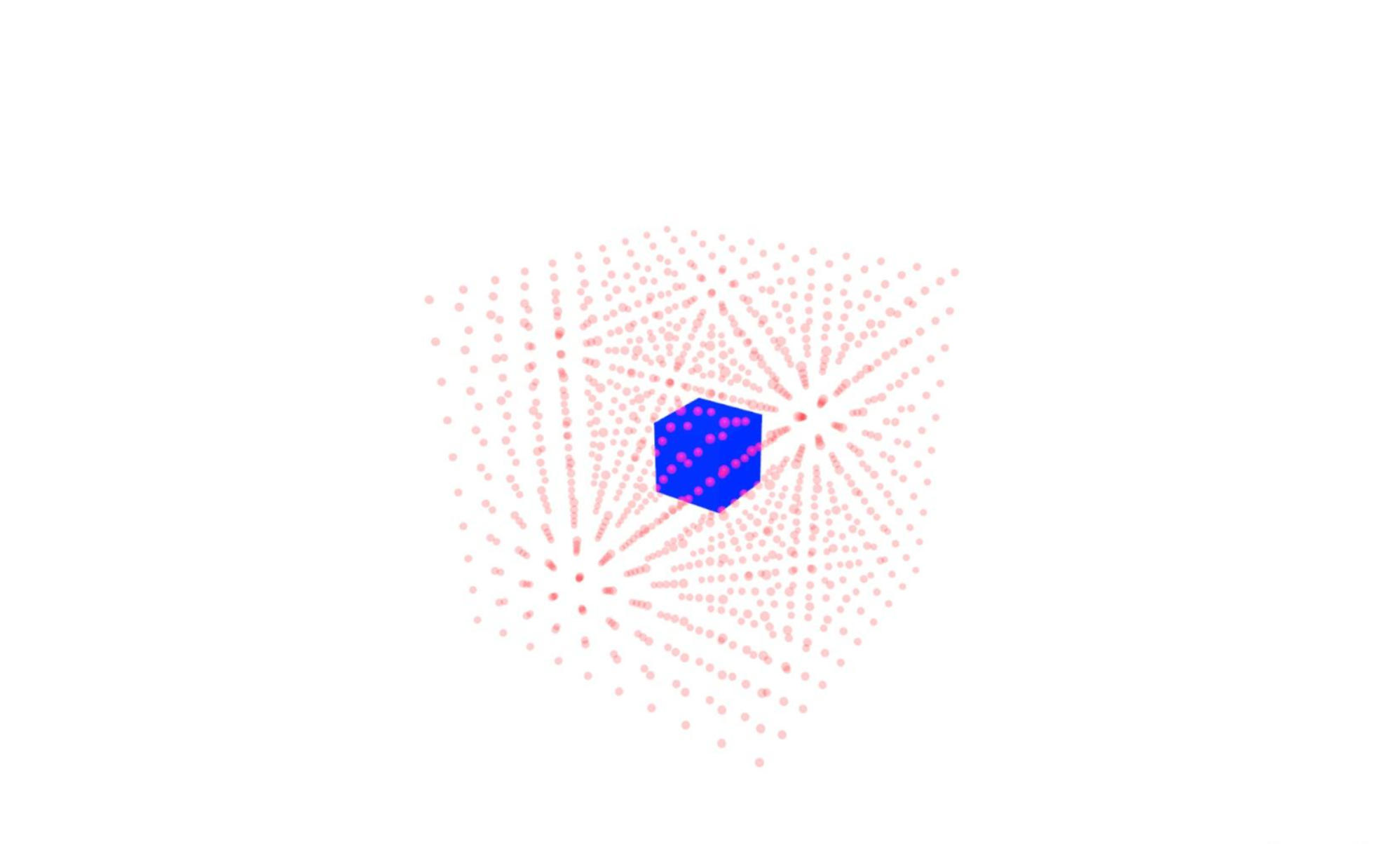
由图所示,我们在一个空间中,按照一定数量和间距摆放一些小球,然后将我们想要计算 MDF 的网格置入这些小球中(有一部分小球会在网格体内)。接下来我们计算每个小球到达网格体表面的最近距离,网格体内小球距离为负数,网格体外小球距离为正数。这些以小球为采样点计算得来的,每个采样点距离网格体的最短距离数据的集合,被称为网格体距离场的体积纹理(mesh distance field volume texture)。上图所示中产生的体积纹理大小为 10 x 10 x 10。有了整个体积纹理,在球体追踪计算时,点到图形距离就可以直接从这个体积纹理中获取。
值得一提的是,每个网格的 MDF 是独立的,它只保存了比网格稍大一些空间内的距离数据(而不是整个场景的,取决于采样点如何安放),也就是说在实际计算中,从体积纹理中获取数据时需要场景空间位置到体积纹理取值位置的映射,这个映射数据也包含在网格体距离场中。
虚幻文档在讲解 MDF 时,由于主语不清晰,很容易导致阅读者以为距离场的计算时在整个场景中进行的,这样在虚幻引擎将 MDF 可视化后得到的视觉效果会让阅读者感到非常疑惑,因为场景中各个网格体之间的距离并没有影响整个可视化的效果,其实是没有搞清楚 MDF 的计算主体。
最后再说一下全局距离场(global distance field,GDF)
GDF 是组合相机视野中的每个 MDF,然后计算合并而得来。因为要集合多个 MDF,所以产生的体积纹理分辨率必然会非常低(不然会很大)。通过虚幻引擎中对 GDF 的可视化结果能够清晰看到低分辨率产生的特点。
图1,空场景中有两个正方体
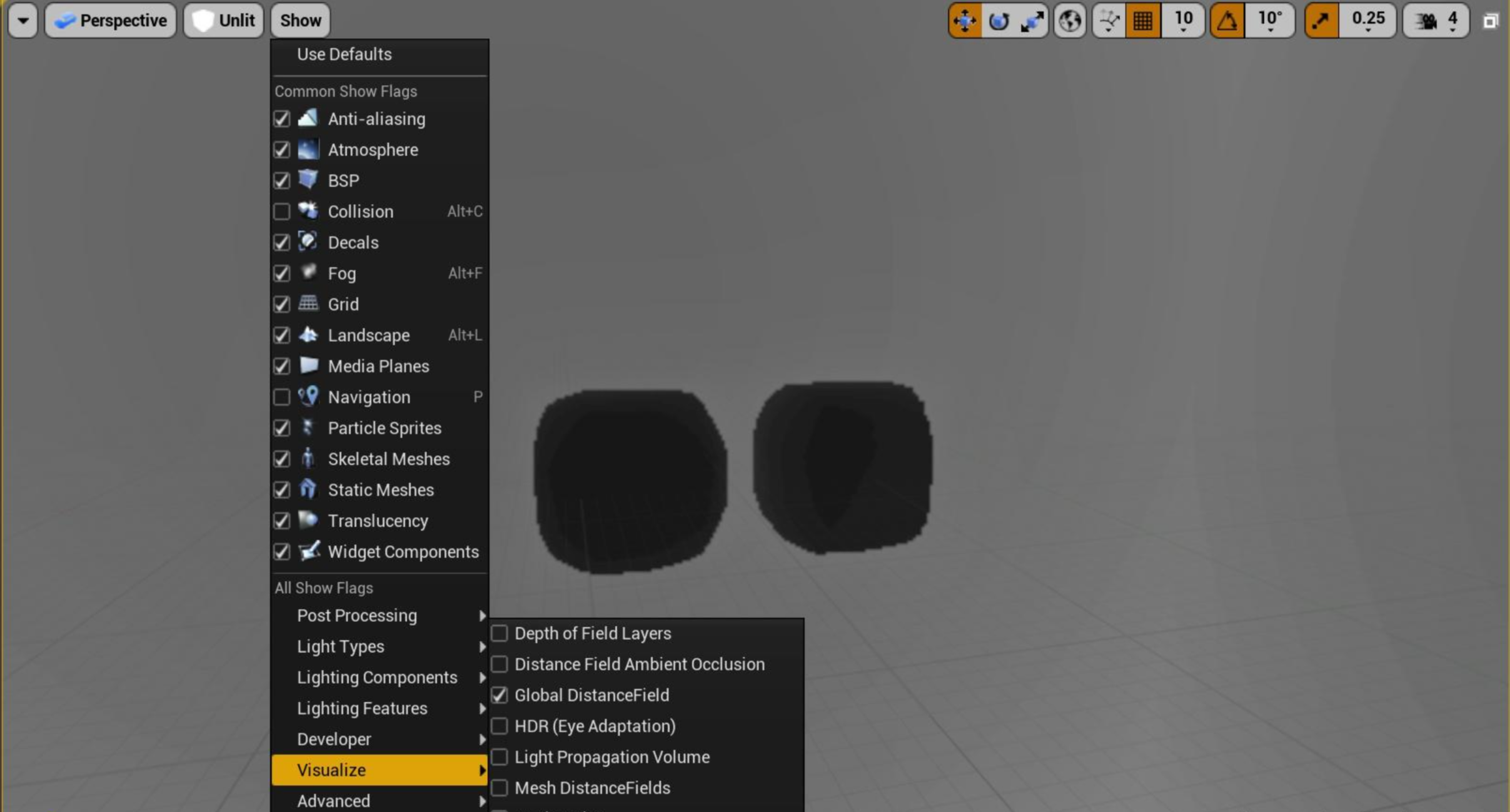
图2,开启 GDF 可视化

图3,让其中一个正方体稍微靠近另一个,还保有空隙,但 GDF 可视化中两个正方体中间的缝隙就会被黑色填补