前言

大家應該都知道,西風系列武器是需要暴擊才能觸發精煉技能的武器,雷主作為一名充能拐,能否觸發武器技能關係到了操作是否流暢的關鍵,如果不暴擊,就需要普攻等補刀觸發,會浪費寶貴的時間,導致循環不暢。那麼雷主該堆多少暴擊率呢?
接下來會涉及一些常用到數學概念,會先作下介紹。
不想看這些數學概念可以翻到最後,看結論就行。
注意這是一篇遊戲心得分享,不是嚴格的數學分析,不嚴謹,希望能幫助你更好地理解遊戲。
一、基本概念介紹
1、隨機事件:在一定條件下,可能發生也可能不發生的試驗結果(outcome)稱為隨機事件,簡稱為事件,通常用西文字母A,B,C,···表示。隨機事件有兩個特殊情況,P=1(必然事件 Ω ) P=0(不可能事件 ∅)
2、概率:事件A發生的可能性大小稱為事件A的概率,用P(A)表示。當試驗的次數足夠大時,可以用 v/n表示該事件概率。
P(A)≈v/n
v表示事件A出現的次數,n表示總試驗數。
3、互斥事件:如果在樣本空間中,事件A與B不可能同時發生,即A∩B=∅,那麼稱A與B時互斥。P(A∩B)=0,即事件A和事件B同時發生的概率為 0。
4、對立事件:是互斥事件中特殊情形,當兩個事件互斥且非A即B(二選一)(概率空間的事件只有兩個)P(A)+P(B)=1且P(A∩B)=0。
5、獨(姆)立事件:
P(A|B)=P(A),P(A∩B)=P(A)*P(B)
即A事件和B事件同時發生的概率是它們各自的概率相乘。如果事件組(集合)A中的事件A1,A2,···,An 互不影響,則
P(A1∩A2∩···∩An)= P(A1)*P(A2)*···*P(An)
二、概率分析
1、思路分析
每次攻擊都是一次試驗,每次試驗包括暴擊事件和不暴擊事件。很明顯,暴擊事件(接下來用事件A表示)和不暴擊事件 (事件B表示)兩個對立事件。
由於每次試驗都有兩種結果(事件),即暴擊和不暴擊結果(事件),三步,每一步的選擇有兩種,所以三次實驗是 2*2*2=8 種可能性(如下圖)。由於每次攻擊事件都與其他事件無關,是獨(姆)立事件。
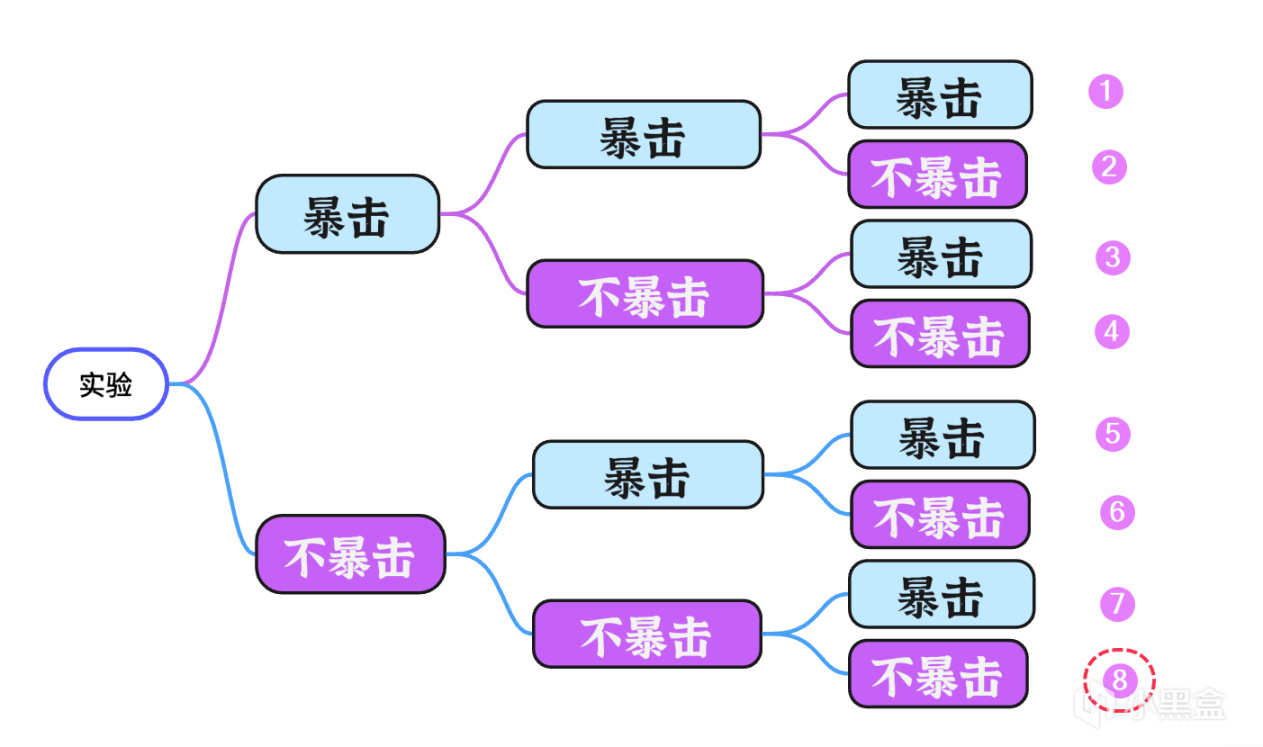
從上圖中可以觀察到 三次全不暴擊 的事件,與有一次暴擊以上事件是互斥事件且對立。這樣我們只要先求得 三次全不暴擊事件 的概率,然後根據

2、建立方程
所以,那麼P(三次全不暴擊的事件),P (三次有一次暴擊的事件)的關係:
P (三次有一次暴擊的事件)= 1-P(三次全不暴擊的事件)
由於每次攻擊都是獨(姆)立事件,互不干擾( 條件概率 P(A|B)=P(A) ),則三次試驗中的概率為:
P(三次全不暴擊的事件)=P(不暴擊)*P(不暴擊)*P(不暴擊)
設雷主的暴擊率為 x(0≤x≤1),即 P(暴擊)= x ,P(不暴擊)概率為 1- x 則:
P (三次有一次暴擊的事件)=1 -(1-x)³
3、圖表分析
畫出二維座標圖形如下
注: 縱座標為P (三次有一次暴擊的事件)或叫做技能暴擊率
橫座標為角色暴擊率x
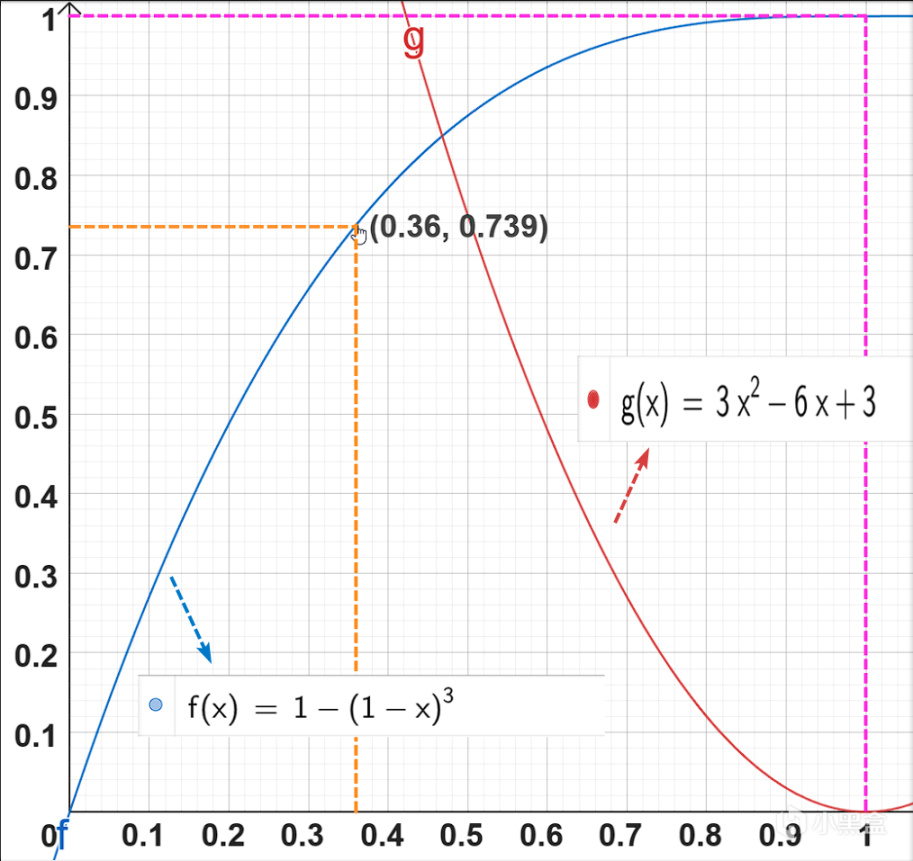
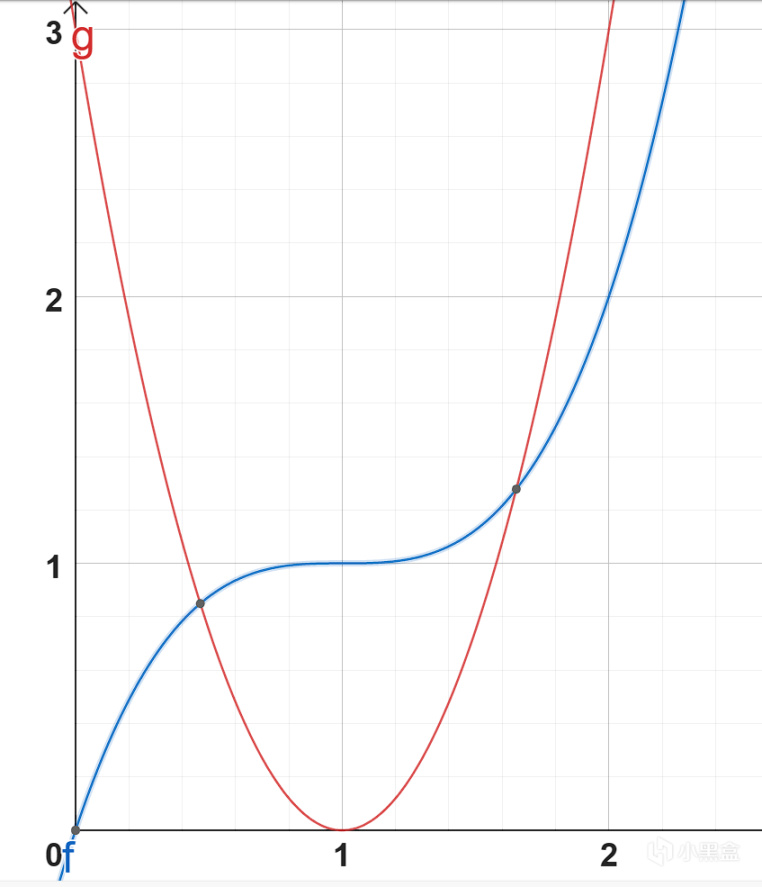
從上圖中可以看到 f(x)函數的導數函數g(x)在0到1區間都是都是下降的,在0.42暴擊率附近,導數就開始小於1(這時對應 三次至少一次暴擊事件 的暴擊率約為 82%,這已經是一個非常高的暴擊率了。)
即一個△x的投入,換來的提升僅僅等於△x或小於△x,不過導數值一直是正的,所以還是有增長,只是增幅會逐漸變低。),之後角色暴擊率的提高對 三次至少一次暴擊事件 的暴擊率的提升越來越小,所以雷主堆個50%暴擊率 就已經非常夠用。(42%暴擊率之前,可以用 角色面板暴擊率*2 粗略估計技能暴擊率,如20%暴擊率面板,20%*2=40%暴擊率)。
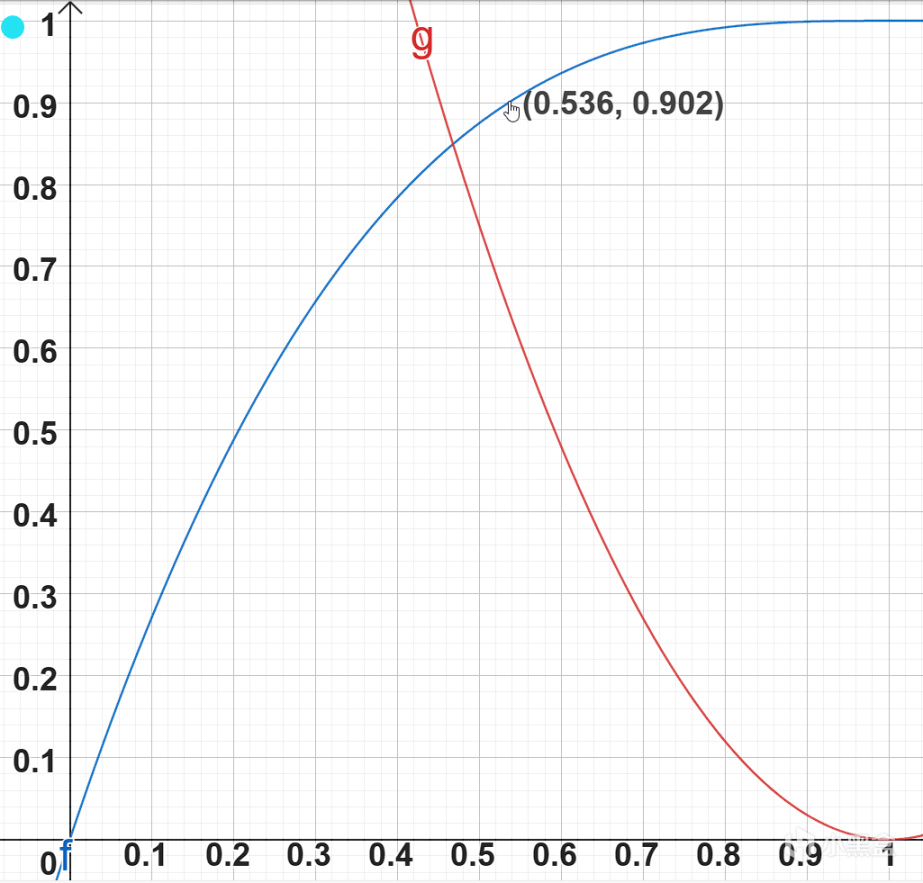
總結
1、低於角色面板爆率≤42%時,可以用 角色面板爆率*2 來粗略估計一次雷影劍暴擊率是
2、55%暴擊率左右對應雷影劍爆率為90%左右,之後的收益就非常低了。 3、不建議為了觸發西風劍等技能堆很高的暴擊率(高於50%暴擊率),收益很低,除非你想堆並能堆到100%暴擊率。
謝謝閱讀,下期再見。
#原神4.1版本創作者徵集活動#