前言

《超凡蜘蛛俠2》這遊戲我雖然沒玩過，不過在大樓之間擺盪的畫面確實很深入人心——在各個角度來說這個系列都是第一方3A遊戲的優等生。

這次粗讀的分享來自Scott Kircher，是Insomniac的核心開發工程師和圖形工程師。

這篇GDC分享吸引我的原因，除了精緻的PPT外，還有就是這篇分享的乾貨密度之高。另一個次要的原因就是這遊戲的規模之大，LOD資源無法由美術人員進行手動調整，因此逼迫了工程師盡全力想出一些辦法來批量和動態優化建築網格，最終得出了不錯的結果。

*由於資料沒有解說稿只有PPT頁，因此還是以翻譯PPT頁內容為主，補充一些我個人的說明。補充說明的內容會標星號。

1 面臨的問題介紹

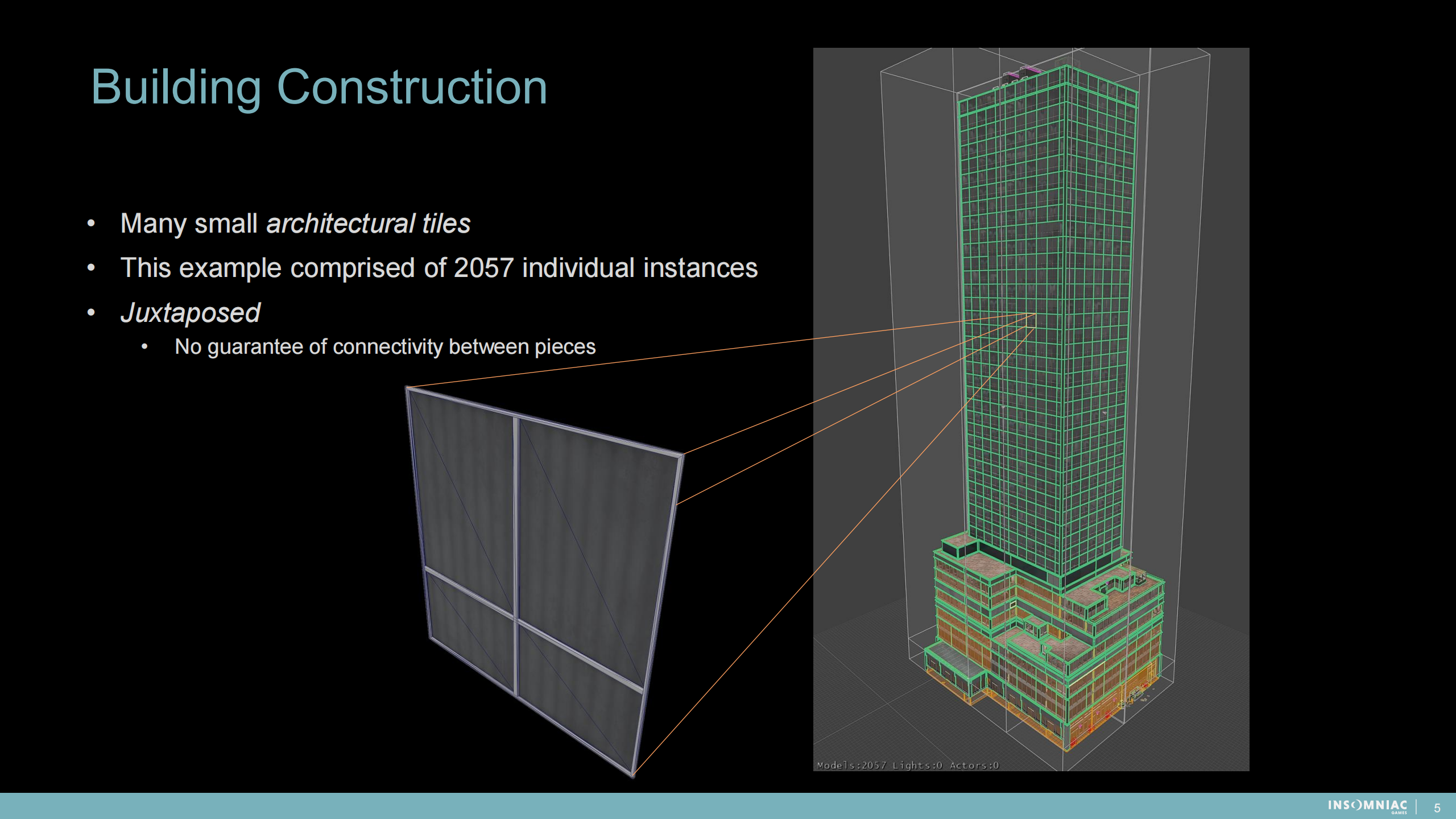
建築結構

許多小的建築塊（tiles——瓦片形式拼接的）
這個例子中包含了2057個獨立的實例
並置的——塊與塊之間沒有連接

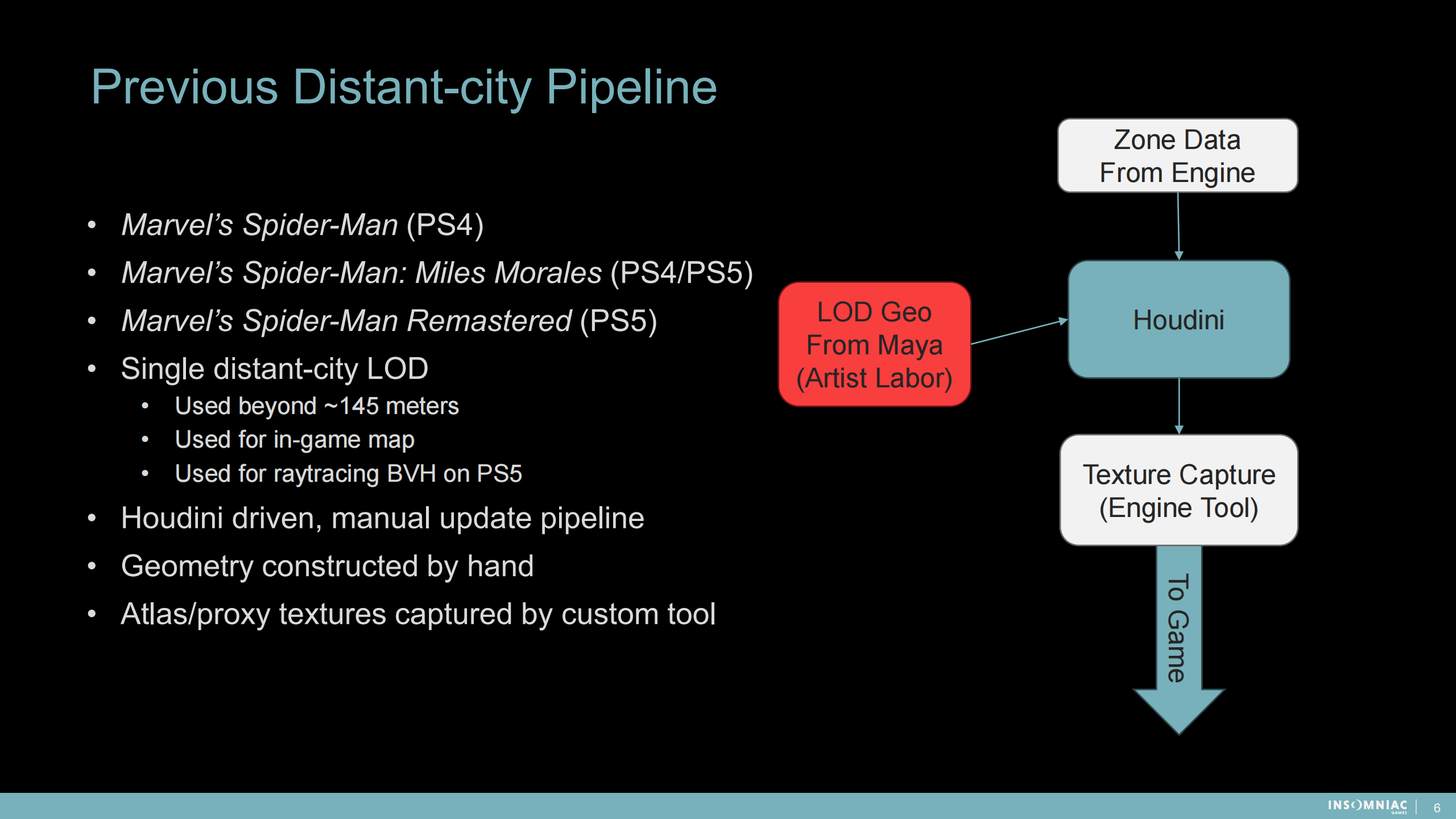
之前的遠距離城市管線

*前幾作遊戲名不翻譯了

單一的遠距離的城市LOD：在超過145米時使用；在遊戲內地圖使用；作為PS5的光追BVH結構。
Houdini驅動，手動更新的管線（Houdini是較新的一款3D建模軟件）
手動構建幾何體
通過自定義工具收集圖集和替代紋理

*關於BVH是一種空間加速結構，之前有文章介紹過。

新管線的目標

1）自動化

減少手工勞動
不再引入更多手工幾何結構
通過構建服務器自動更新LOD（這個是構建工具鏈的概念，不是運行時的server）

2）提升質量

兩層主要LOD：高密度、中等距離；低密度、遠距離。
兩層光追的BVH LOD：中等密度、中等距離；低密度、遠距離。

重大的工程限制

1）遊戲已經幾乎完成了

產品還剩大約一年半時間
建築的結構幾乎已經完成了

2）16位索引格式

每個建築最大65535個頂點（2的16次方）
適配已有的遊戲系統並節省內存
儘量不要重構很多不熟悉的代碼

3）內存、磁盤空間的緊缺

——頂點格式：每個頂點4字節

10位的壓縮後的座標
沒有頂點法線或UV

——法線貼圖需要被節儉地使用

節省內存
僅表現曲面時需要，避免其它情況

*整體來說，就是在工期有限、性能空間有限的情況下，需要把一層LOD想方設法調整成2層LOD，以提升畫質併為光線追蹤提供BVH數據。

2 網格簡化——及帶來的問題

通過Simplygon減少網格數

——已經購買了SImplygon的授權

用於常規（非距離化）的LOD

——通過網格減少工具反覆簡化網格

需要焊接步驟
（適用於）相似的幾何與拓撲結構
對於非流形結構沒有幫助（non-manifoldness 特指有多個面共享一個邊的網格）
構成了每個建築最初的距離LOD

通過Simplygon重構網格

——網格重構生成了完全新的網格

類似的幾何結構
無關的連接性或拓撲結構
消除了非流形的邊緣
可能非常昂貴——高密度的輸出可能需要好幾個小時
每個建築需要生成次一級距離的LOD——加上生成BVH，工作量又加倍了

重構網格+網格減面的超級混合方案

——為我們提供了建築結構

減少網格工具對於較高密度LOD工作良好
重構網格工具對於低密度LOD工作良好
兩者之間如何呢？

——第一級遠距離城市BVH LOD（中等質量和密度的）

平衡質量和內存
需要“中等的”密度
減少網格工具會打散並置的建築塊
重構網格工具的結果不太對：偏差太大、或是輸出了太多頂點

——解決方案

對過分保守的目標物重構網格
然後（把網格）減少到需要的密度

那麼，問題是什麼呢？

——需要記得那些工程上的限制

建築數據結構“不可修改”
16位
4字節頂點
儘量減少法線貼圖的使用

——通過Simplygon的減少網格和重構網格工具是不夠的

——三個主要問題

缺少法線信息
（被錯誤）網格重構的“內殼”
網格減少導致破皮、裂開問題

問題1：缺少法線信息

——頂點格式中僅包含位置（座標）數據，沒有法線數據

——（幾乎）沒有法線貼圖

——法線是在運行時、逐三角面計算的（像舊的flat-shading一樣）

——自動化的網格減少和重構會打亂表面結構

本來平整的結構會不再平整
看起來有鑲嵌感
“三角定位故障”

*很多都是自動減面工具的一些常規問題，這類工具很難理想地處理結構稍微複雜的網格體。

問題2：網格重構的“內殼”

——（原本的）建築結構通常會顯得“空洞”

通常都是未封閉的
包含一些並非實際開放的邊界
一些建築塊包含背面結構

——重構後帶來一個封閉的網格

建築表面被錯誤摺疊在“建築內部”
這被稱為“內殼”

——（這種額外多出的內殼）比較浪費性能

——會帶來光追上的潛在問題

問題3：網格減少後的裂開、破皮

並置的結構塊
建築塊可能有內部縫隙——未連接或內部有穿插的幾何結構
縫合不能解決所有問題
減少網格可能帶來頂點移動——帶來一些視覺上的縫隙
會導致漏光問題

“額外的”問題

建築結構基本避免了法線貼圖的使用
對於曲面該如何處理？——法線貼圖或至少頂點法線是需要的
對於上千個需要處理距離LOD的物體，能自動檢測出需要法線貼圖的物體麼？

*這一段很細緻的介紹了建築這種看起來方方正正的網格結構體在使用自動化減面工具時遇到的各種問題。由於前面也介紹過，自動化處理的方案是必須執行的，所以後續他們對自動化處理後的網格需要逐一解決這些問題——這也是這篇分享乾貨的開始。

3 三角網格分析

幾何結構連接性拓撲結構

——幾何結構

表面的“形”
頂點的位置
可通過（頂點的）插值計算三角面上的位置

——連接性

頂點通過邊連接
三角面由邊構成

——拓撲結構

在連續的變形中表面具備的不變性
例如：一個表面有多少個洞
可以僅通過連接性（不通過幾何結構）進行推導

流形網格

流形邊緣——嚴格由兩個面共享一條邊
流形網格——所有邊緣都是嚴格由兩個面共享的

*配圖中展示了流形和非流形的區別。Manifold一詞更多表示“具有多樣性的”，簡化成專有名詞後確實丟失了很多信息。

（結構的）屬

——屬是一個形體上“洞”的數量

並非所有洞都是由形體邊緣產生
用來度量拓撲結構的“複雜度”

——歐拉示性數（公式）

可以被用來計算流形三角面網格的屬

*這裡摘一段對歐拉示性數簡要的分析：

其中V代表頂點數，E代表邊數，F代表面數。對於與球面同胚的多面體，歐拉示性數恆等於2。然而，並不是所有物體的歐拉示性數都為2，例如環面的歐拉示性數為0。

此外，歐拉示性數還可以通過公式2-2g來計算，其中g指的是閉可定向曲面的虧格數（即有多少個洞）。這個公式揭示了歐拉示性數與虧格數之間的關係。（上面則是一個反算過程）

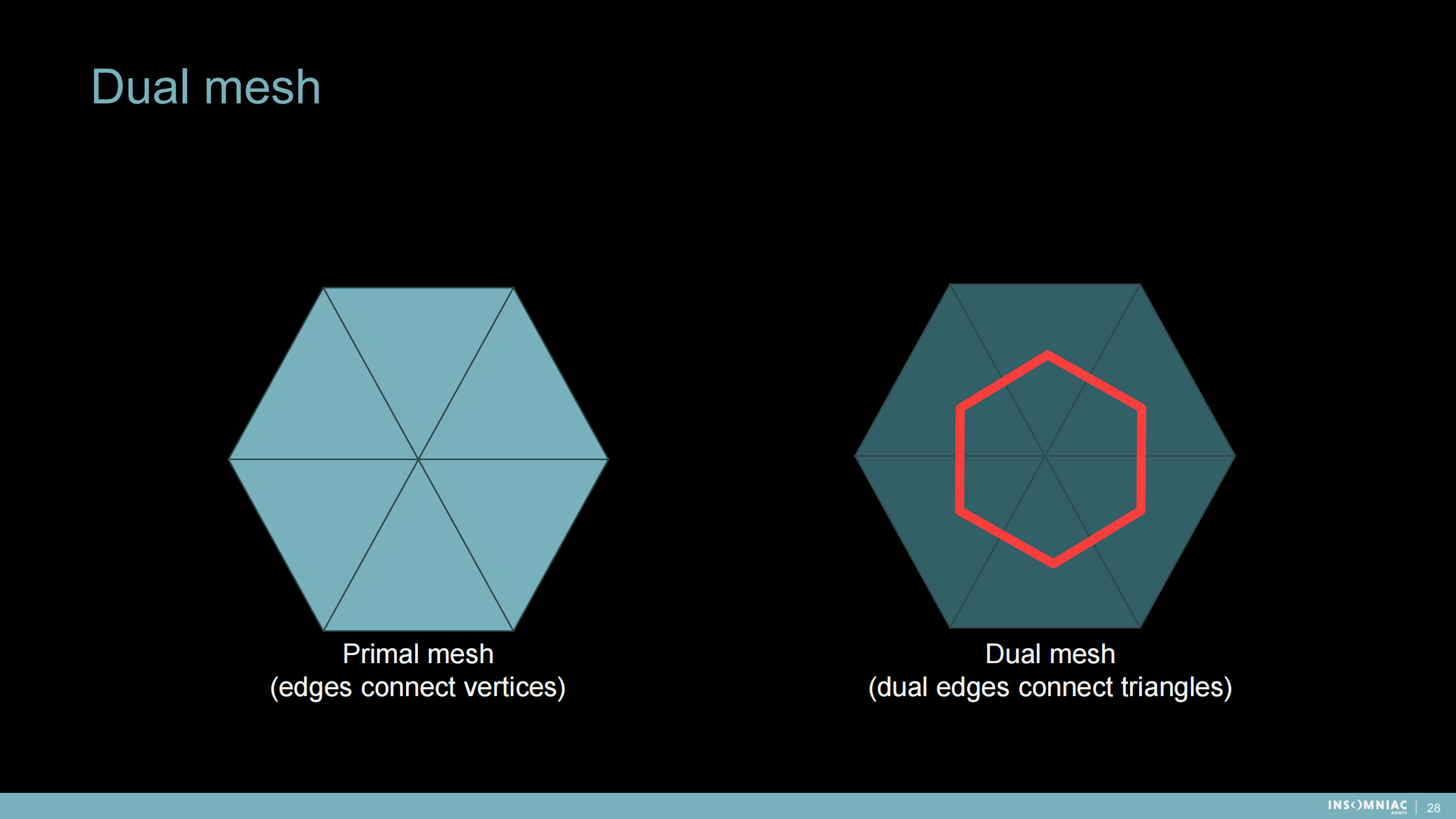
雙重網格

*雙重網格增加了一層邊用來連接三角面的中心。

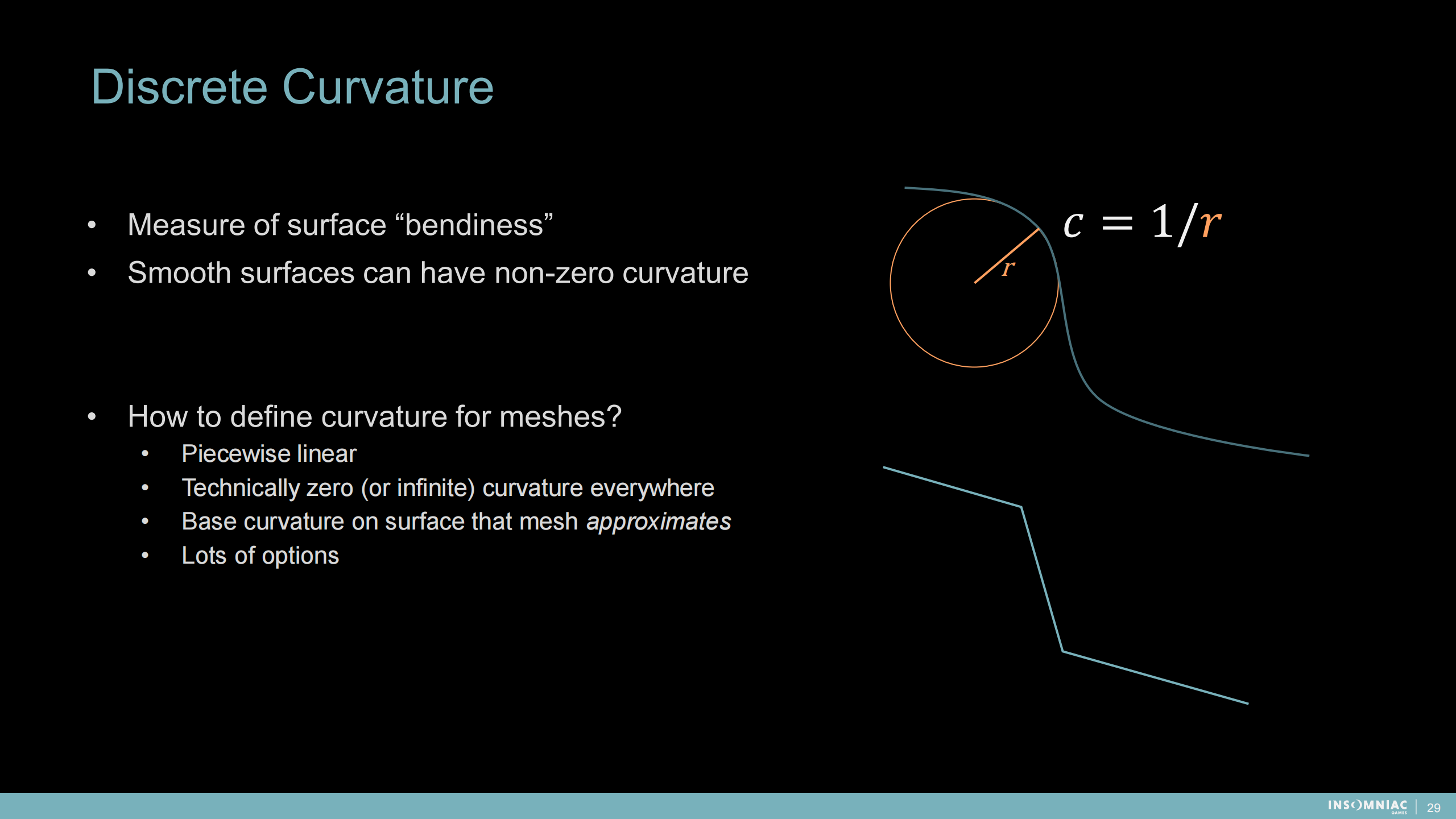
離散曲率

——用來度量表面的“彎曲度”

——平滑表面也可能有非零的曲率

——如何定義網格的曲率？

分段線性
各處有很多零（或無限）的曲率
表面的基礎曲率可以作為網格的近似
有很多備選方案

*關於離散曲率是一個複雜課題，離散分段法只是一種基礎的方式，更多推導方式我也沒有能力全面介紹。文末會附一篇資料鏈接。

*這裡介紹的這些數學工具主要就是用來解決之前提到的3+1個問題的。

4 網格平整

主要思想

——（整體的）光照著色比輪廓形體更重要

尤其對於遠距離LOD
尤其對於本應是平整的表面

——在網格減少時保存法線信息

在Simplygon減面工具中提高法線權重
在後續導出時取消這一設置（最終結果是不包含頂點法線的）
可以幫助減少結果的偏差
僅靠這個工具自身是不足夠的
對於重構網格則完全不適用

——核心思想：平整減面後的網格

修改幾何體，使單獨的三角面法線適配預期的法線方向

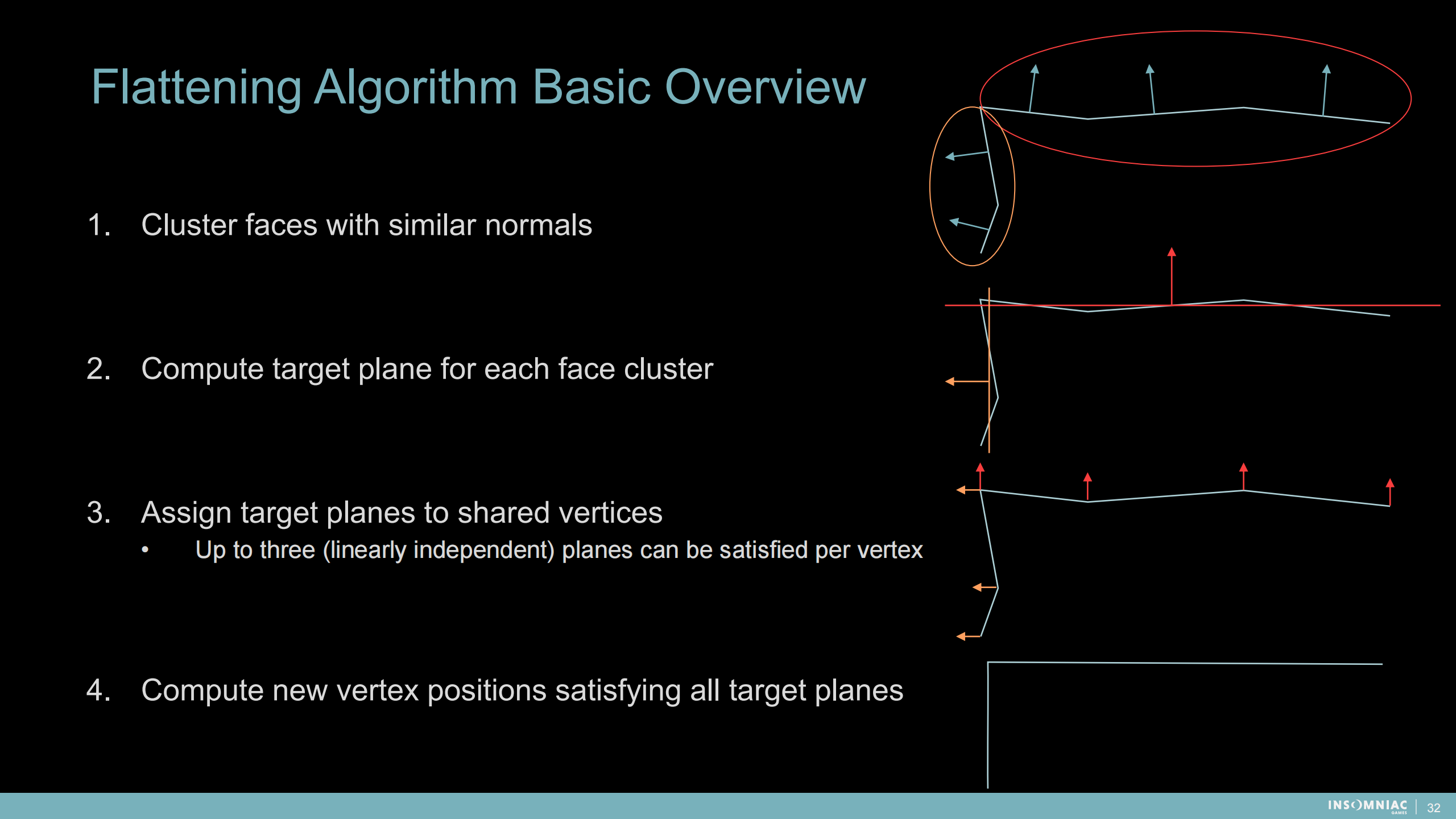
平整算法概述

將有相似法線的面集群化
對每個集群計算目標平面
將（平面位置和法線信息）分派到共享的頂點上——每個頂點滿足最多三個（線性獨立）的平面
計算滿足所有新平面的頂點位置

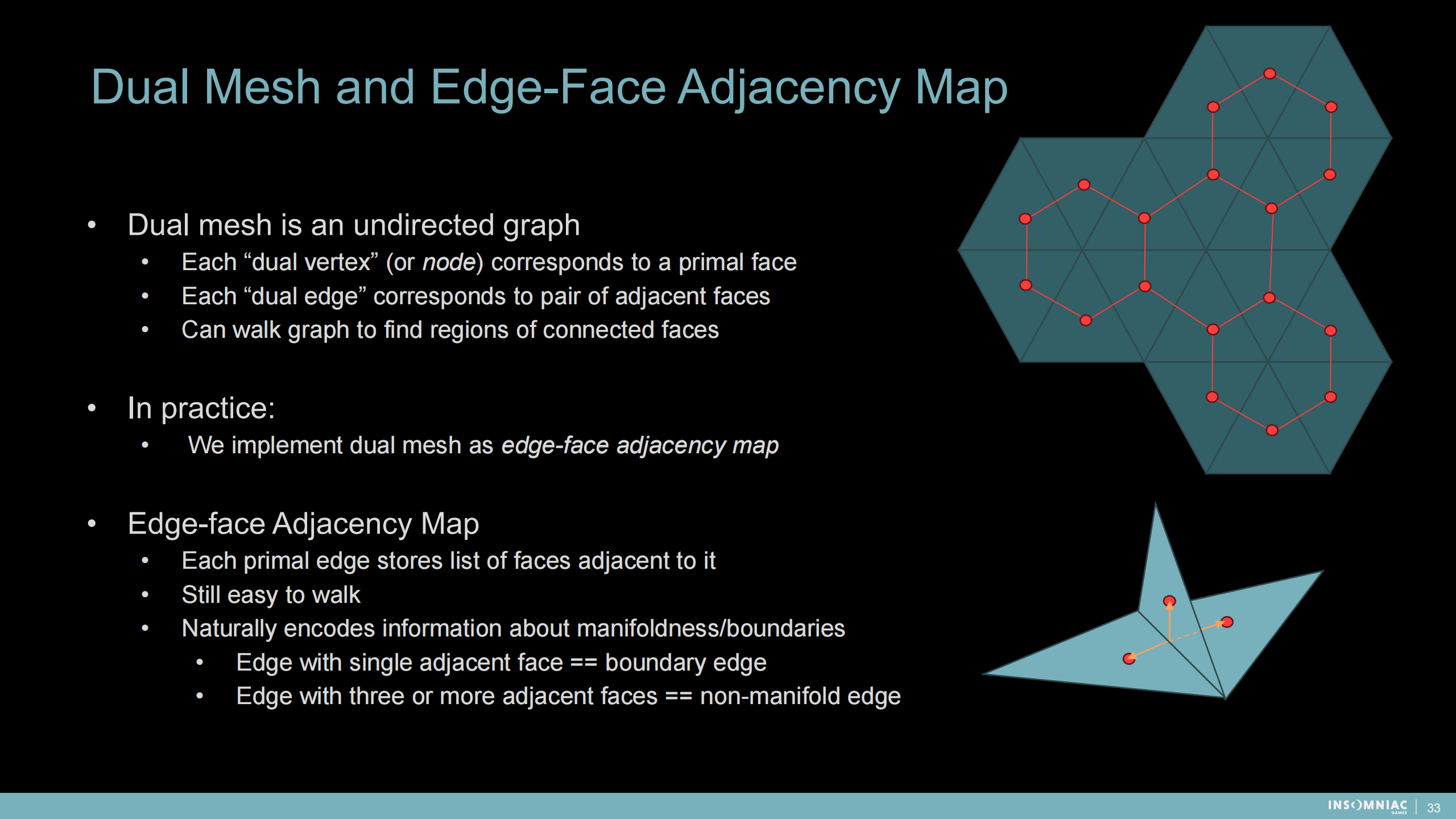
雙重網格和邊面連接圖（這裡圖是一種數學結構）

——雙重網格是一種無向圖結構

每個“雙重頂點”（或節點）對應一個三角面
每一個“雙重邊”對應一對連接的面
可以遍歷圖來查詢面之間相連的區域

——在實際應用中，我們採用了邊面連接圖（作為數據結構）。

——邊面連接圖

每個原始邊存儲與之相連的面的列表
仍然易於遍歷
可以自然地編碼流形和邊緣信息（通過連接數）：單獨連接面的邊——邊緣邊；連接三個或更多面的邊——非流形邊。

步驟1：將有近似法線的面劃為一個集群

A. 選擇下一個集群的種子面——（區域中）最大的為劃入集群的面。

B. 遍歷邊面連接圖（雙重網格）

廣度優先遍歷
不訪問和種子法線差距“太大”的面
這組訪問到的面的集合構成了新集群

C. 如果存在未訪問的面，重複步驟A

面的法線相似度

比較面的法線——始終和種子面進行比較（前述選擇用來開啟新集群的面）
對於網格減少的結果——可以使用（減面過程保存的）原頂點的法線數據；可以得到和原始網格很接近的著色結果
對於網格重構的結果——直接使用計算後的表面法線

步驟2：為每個面集群計算目標平面

直接計算集群區域內的各面的平均值（逐集群）。
可以對集群內的點做最小平方擬合——非必須，因為集群在其結構上已經是“最平方案”了。

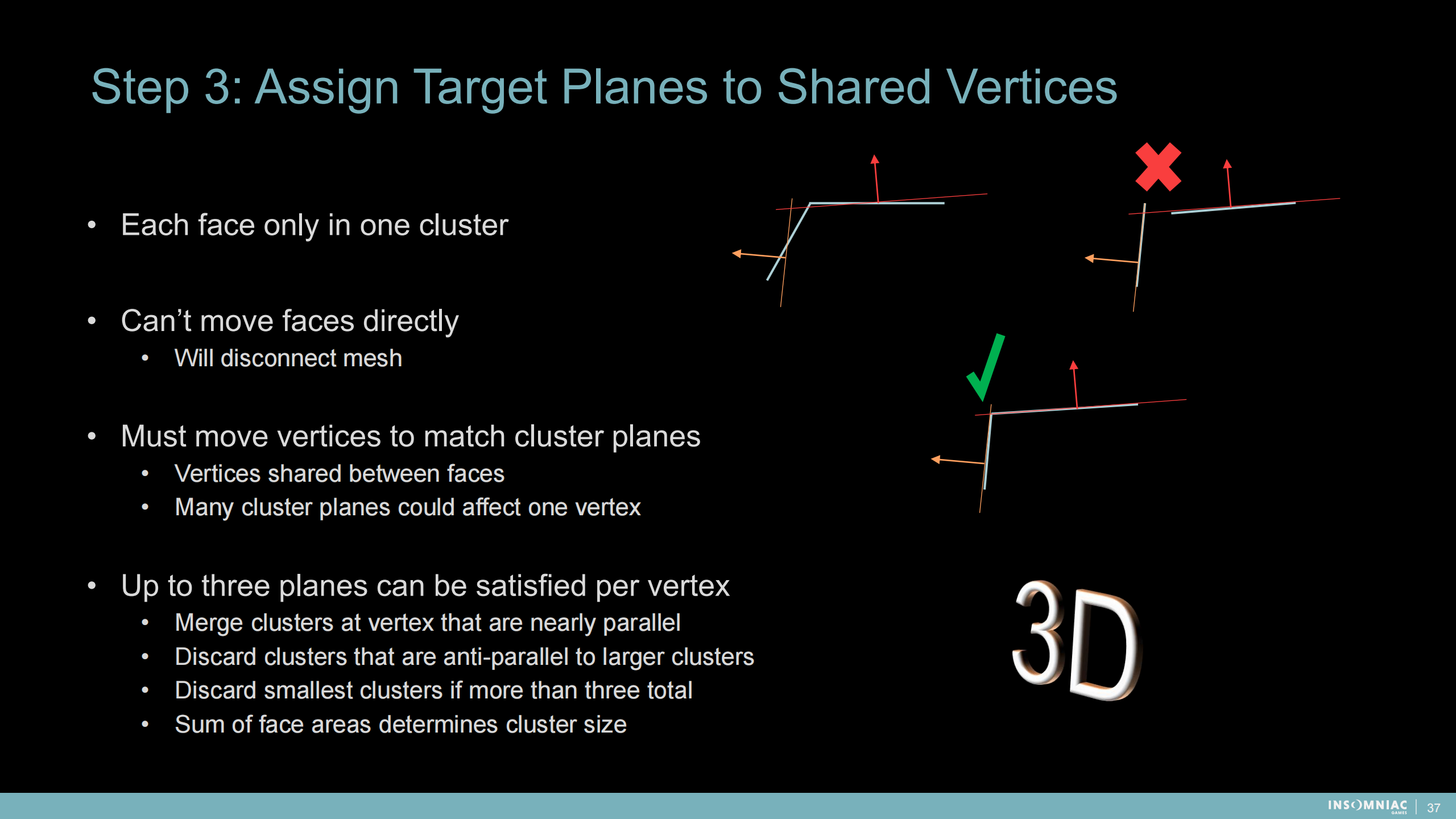
步驟3：分配平面屬性到共享的頂點

——每一個面只屬於一個集群

——不能直接移除這些面——會帶來不連接的網格

——必須移動頂點來適配集群平面

頂點可能被多個面共享
多個集群平面可能影響同一個頂點

——每個頂點最多滿足3個平面

頂點處的合併集群是集合平行的
取消（頂點處）與大的集群不平行的小集群
取消（頂點處）大於3的小集群
集群的大小用內含的面的個數來計算

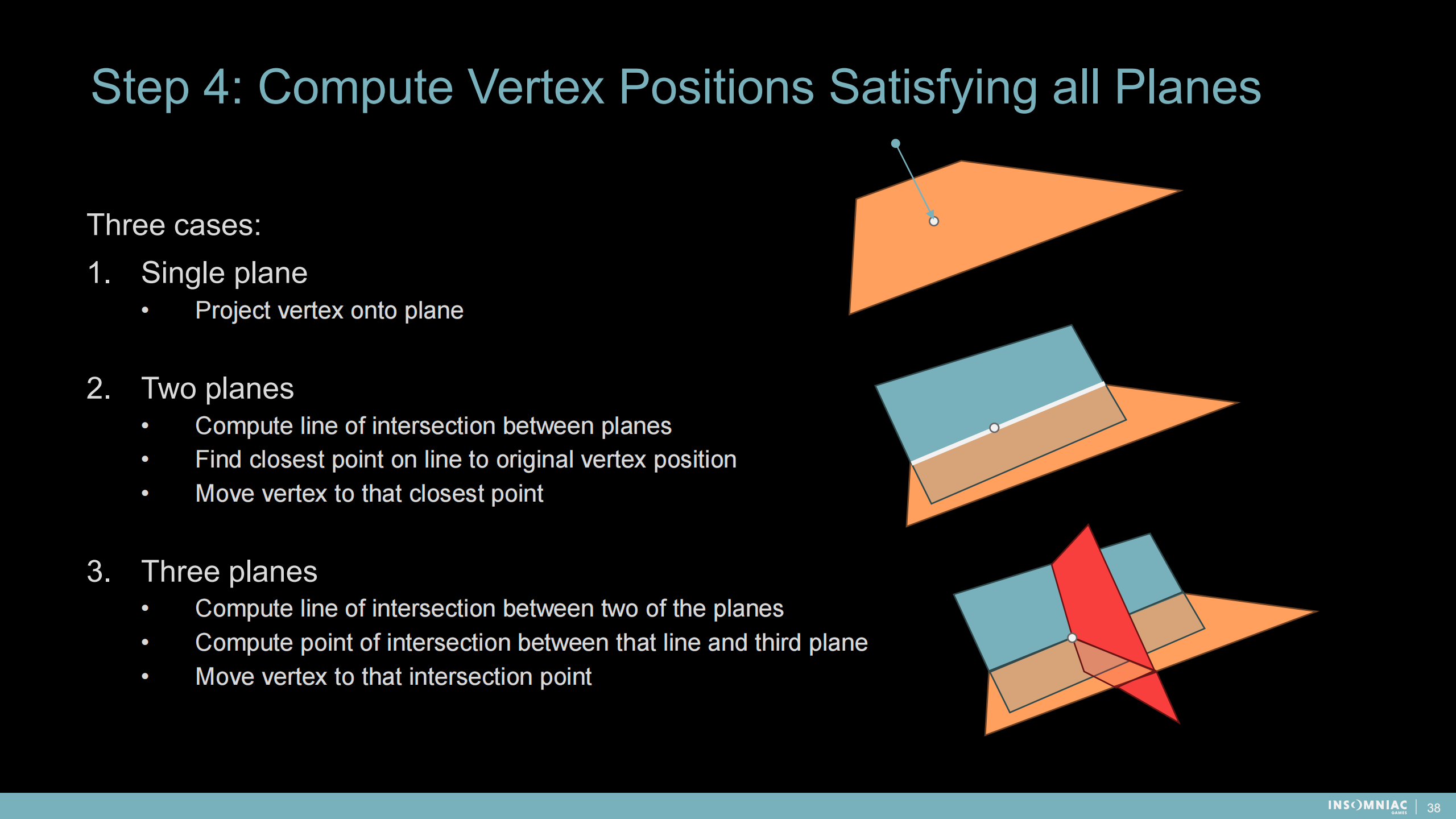
步驟4：計算滿足所有相關平面的頂點位置

三種情況：

1）單平面——把頂點投影到平面

2）雙平面——計算平面的相交線；找到頂點位置到線上最近的點（投影到線）；移動頂點到那個最近的點

3）三平面

計算任意兩平面的相交線
計算線與第三平面的交點
把頂點移到該點位置

平整後的結果

5 內部結構分類——解決“內殼”問題

核心思想

粗略地將面分為內部和外部
局部信息是不足夠的——對凹面形體來說法線方向是沒意義的
需要一些全局信息（仍然很難）
使用“氾濫填充”（遍歷雙重網格）來解決——目標：獲得一個連接體內的內部面的連續集合。

內部結構分類基本算法

基於Stochastic射線檢測方案（離線工具）

1）識別出少量的內部點

用蒙特卡洛採樣的方式，在包圍盒的水平展開的範圍內採樣

2）內部面集合的分類

從每個內部點，對每個面發出射線
檢測每個面是否能“看到”該內部點（基礎計算可以去看Games101）

3）最終進行氾濫填充

生成一組相連的內部面的單一集合
（以及一組外部面的集合）

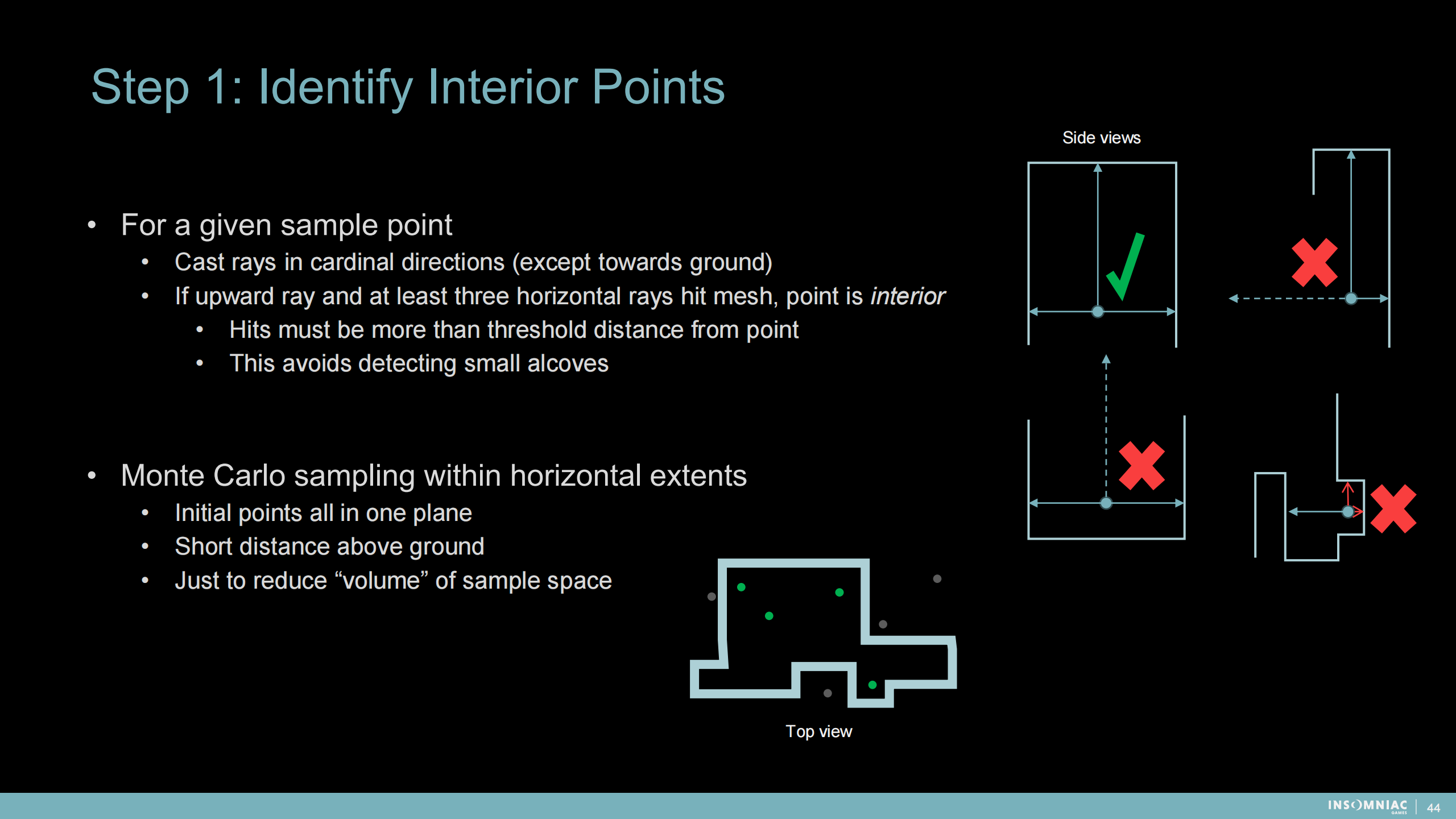
步驟1：識別內部點

1）對於一個給定的採樣點：

對基本的方向（可以理解成軸向的）發出射線——地面方向除外。

如果向上的射線和至少3根水平射線命中了網格，則點是內部點。

命中位置與起點距離必須大於距離閾值
這可以避免檢測出小的壁凹

2）水平展開的蒙特卡洛採樣：

所有初始點都在一個平面內
在地面上方一小段距離
目的是減少採樣空間的“體積”

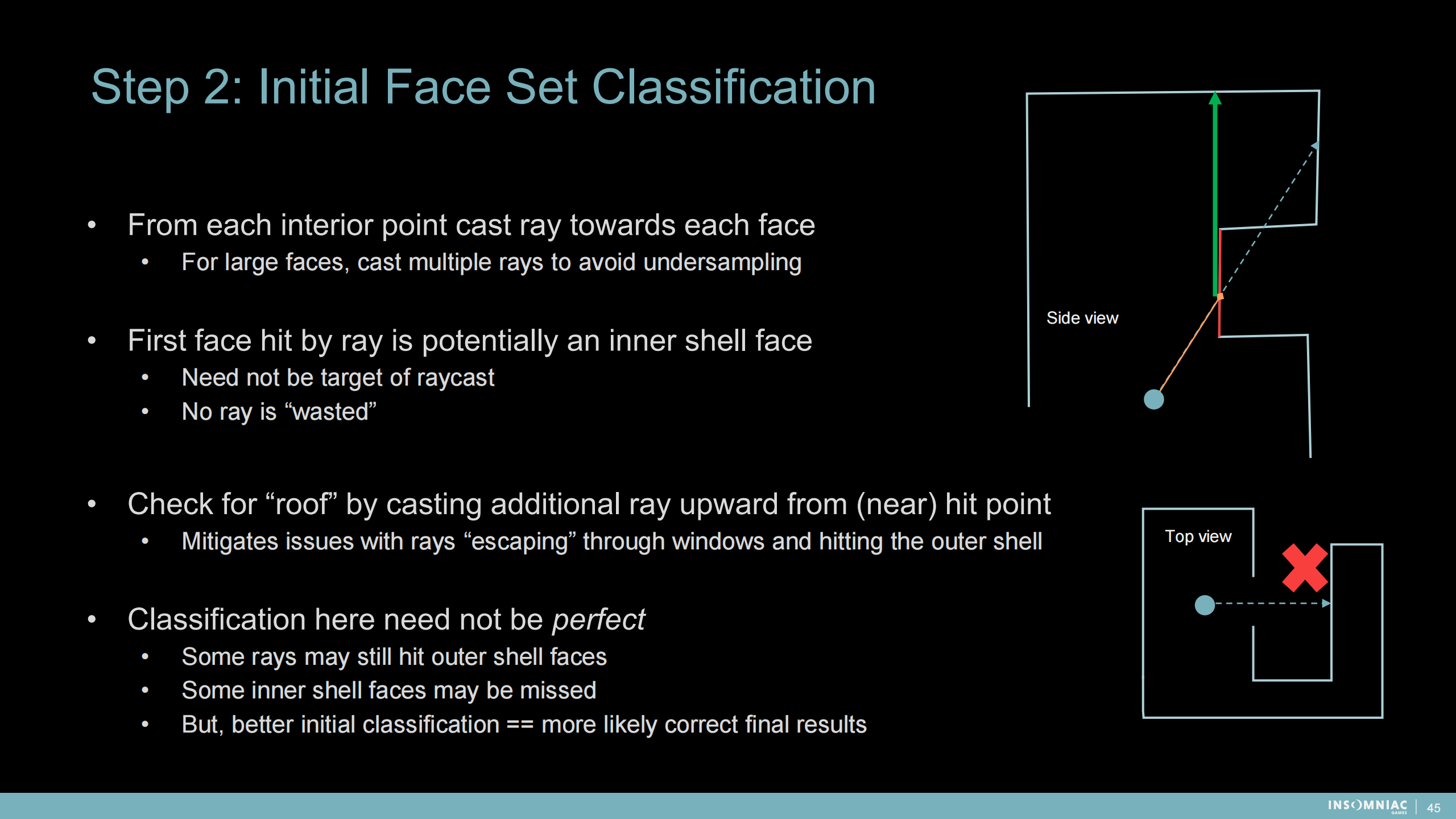
步驟2：內部面集合的分類

1）從每個內部點向每個面發出射線

對於大平面可以發出多條射線以避免採樣不足

2）第一個命中的面是一個潛在的內殼面

需要將其不視為射線檢測的目標
這樣可以避免射線的“浪費”

3）通過從命中點（或附近）射出額外的向上射線來檢測“房頂”

減少射線通過窗口位置“逃逸”並命中外殼的問題

4）這裡的分類方式不需要是完美的

仍可能有部分射線命中外殼
可能漏掉一些內殼的面
不過，更好的初始分類就更接近正確的結果

步驟3：氾濫填充修正

從每個外殼面遍歷雙重網格

只遍歷至其它外殼面
找到外殼面的連續集

步驟3：氾濫填充修正

保留最大的外殼面集合——將其它的標註為內殼
重複處理內殼面——找到內殼面的連續集

步驟3：氾濫填充修正

保留最大的內殼面集合——將其它的標記為外殼。
現在我們找到了一個單一的連續內殼

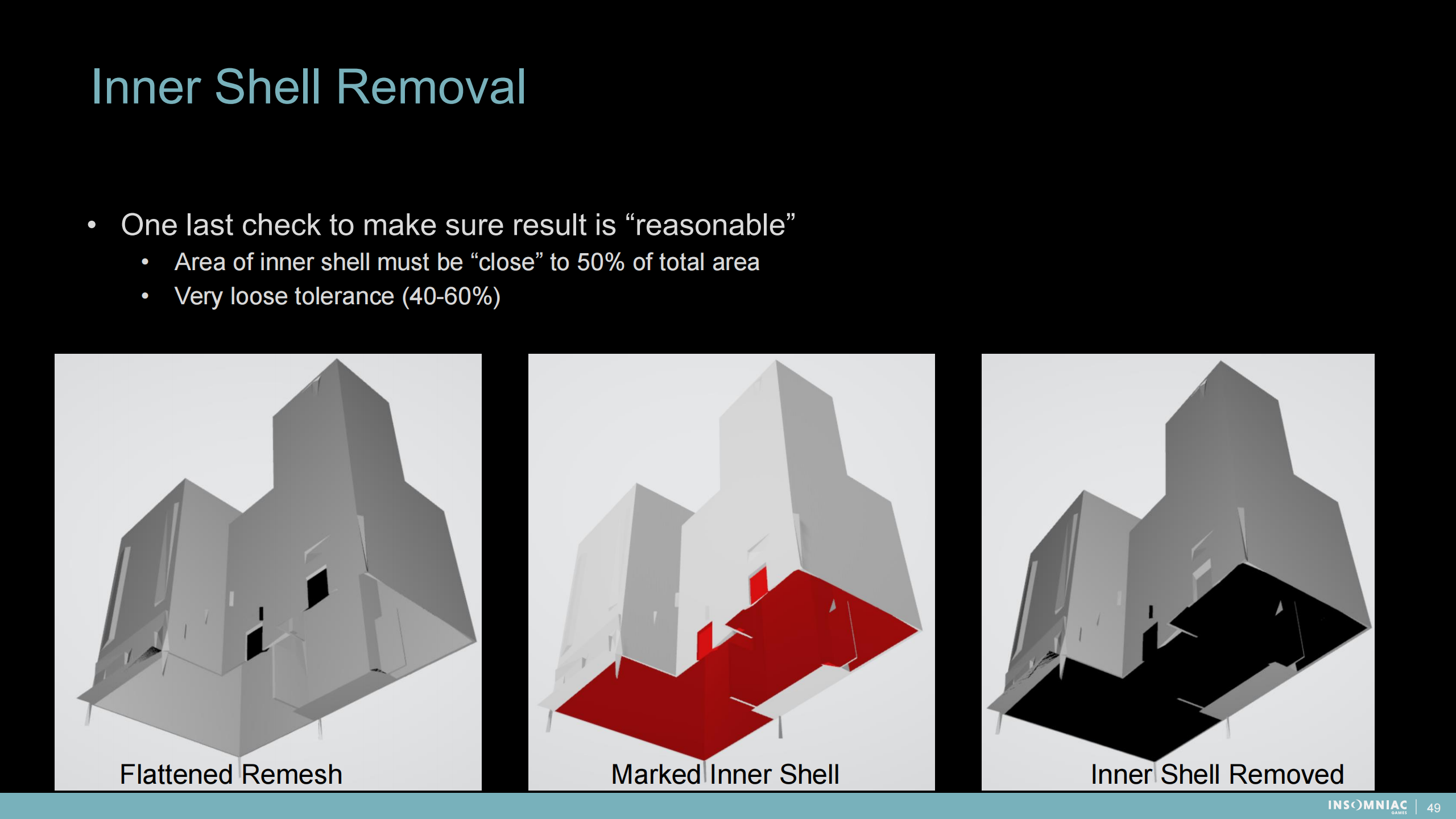
“內殼”移除

最終檢查步驟以保證結果是“合理的”：

內殼區域必須“接近”50%總區域範圍
可以有比較鬆散的容差空間（40-60%）

*通過移除之前工具生成的“內殼”，可以減少大量不可視網格的渲染計算，最終提升性能。

6 生成支撐物——解決網格裂開問題

核心思想

必須移除網格減少導致的裂開問題——消除漏光（影）問題
觀察：網格重構後的內殼能較好適配原始網格的內部——並且，它是一個單一連續無破皮的體塊

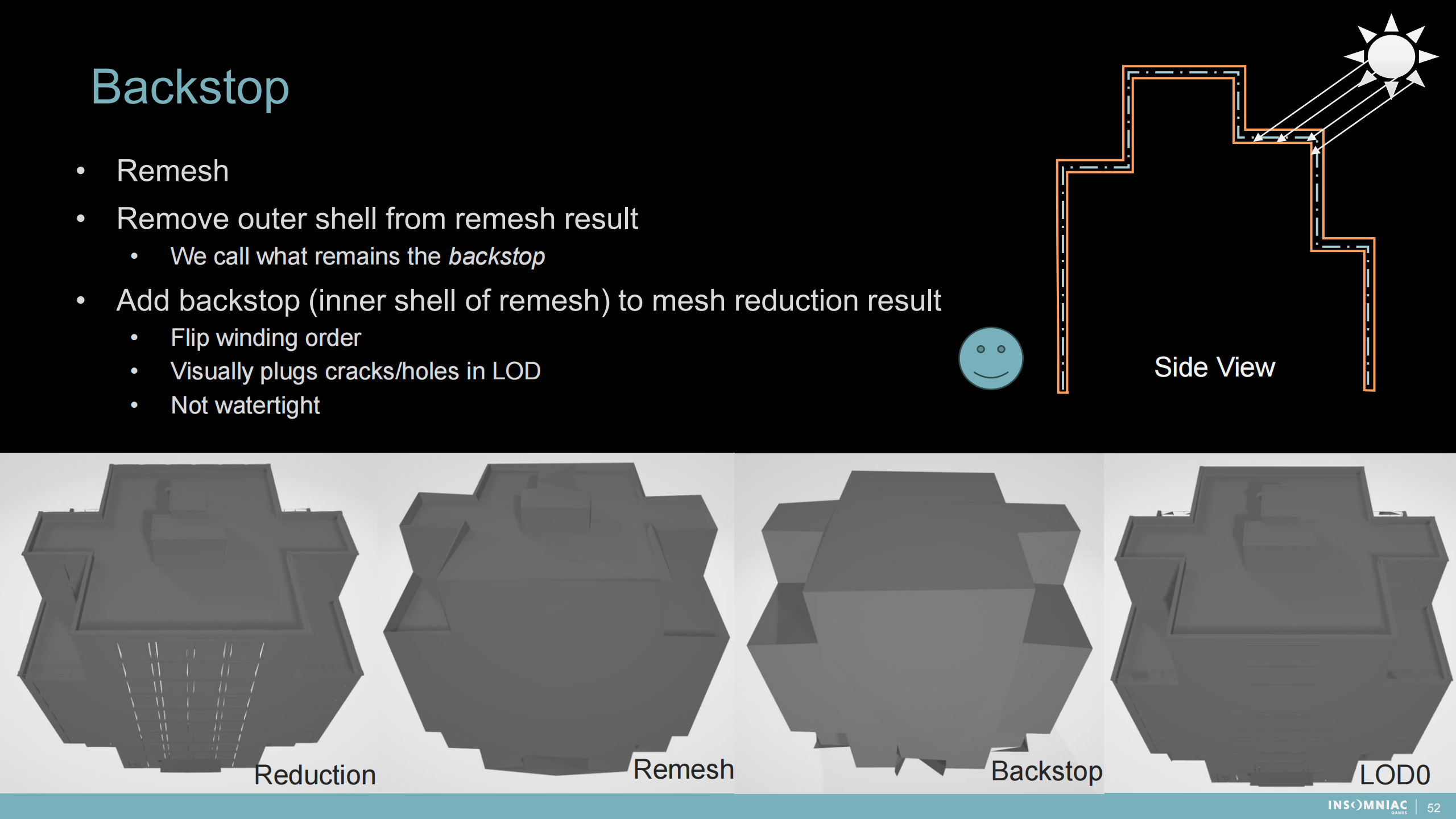
支撐物

*backstop有很多不貼合這種情況的翻譯，支撐物只是相對合適的一個。

1）重構網格

2）移除重構結果的外殼——我們把餘下的部分稱為支撐物

3）將支撐物（內殼或重構後的網格）添加到網格重構後的結果中

翻轉繞序
視覺上堵住LOD的裂開或洞
結果並不是天衣無縫的

*繞序翻轉的作用是把本來向內的網格朝外。

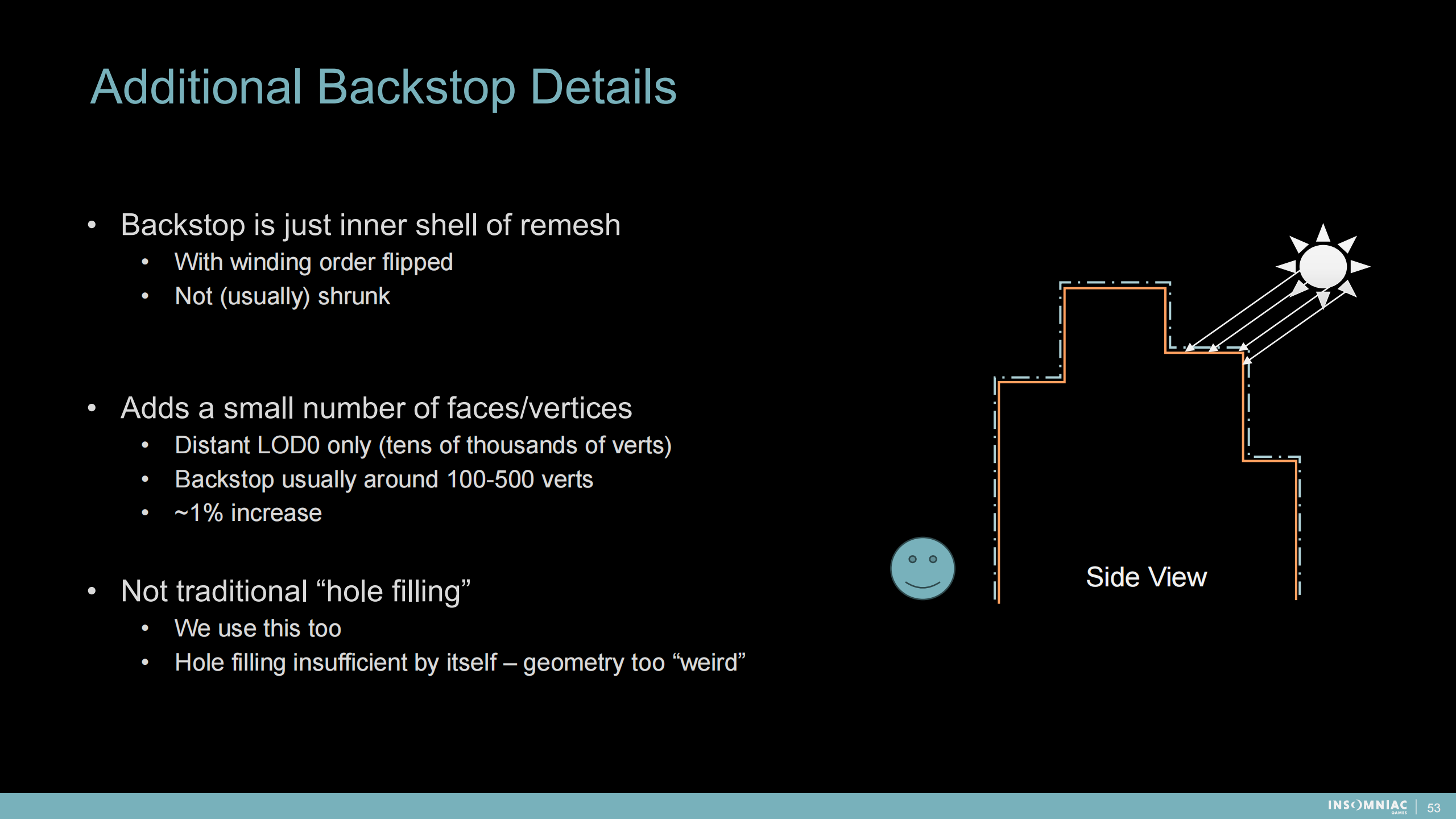
額外的支撐物細節

1）支撐物只是內殼或重構的網格

經過繞序翻轉
（通常）不縮小

2）添加了少量的面或頂點

僅用於遠距離LOD（成千上萬的頂點）
支撐物通常在100-500頂點
整體約增加了1%

3）不是傳統的“補洞”方案

我們也使用了傳統補洞工具
補洞工具有其自身的不合適之處——補充的幾何體結構過於“奇怪”了

支撐物後備方案

1）重構的網格內殼不是總存在

原始網格可能已經（幾乎）完全封閉了

2）備選方案

將網格重構的結果沿著其法線方向輕微收縮
翻轉背面

3）從輪廓上可能看到細邊緣的視覺錯誤

所以，儘量還是使用內殼作為支撐物

不適合使用支撐物的建築結構

城市中並非所有建築都是大樓
支撐物不適合某些物體——有其是橋和類似的輔助結構

檢查不適合使用支撐物的建築結構

1）觀察：橋或輔助結構通常有很多的“洞”

2）可以使用拓撲結構的屬來自動探測

大樓建築有相對低的屬
橋有非常高的屬

3）想要忽略輕微的裂開和非流形的情況

Simplygon網格重構帶給我們沒有“小”洞的流形網格
計算重構網格的屬

4）同時使用一個表面區域閾值

大樓建築應該有更大的表面區域
雕像或其它物體有更小的表面區域

5）藝術家可以強制覆蓋（支撐物結果）

強制開啟
強制關閉

7 自動探測法線貼圖

核心思想

曲率分析
計算並估計一些視覺上明顯的曲率——有著高視覺曲率的建築需要有法線貼圖；其它的，“大概”就不需要。

我們的離散曲率定義

直覺：原始網格表面的法線和表面的曲率相關
曲率和表面切線所在圓的半徑反相關
考慮面上的一條邊（如圖）

*圖中是一些向量計算，包括後面整個方案基本也是向量級別的計算。

面的曲率和麵的集群

我們關注於一個網格區域的“總”曲率數值
以邊長權重作為邊曲率的平均值，來估計面的曲率（直接看公式即可）
以面積權重作為面曲率的平均值，來估計面集群的曲率

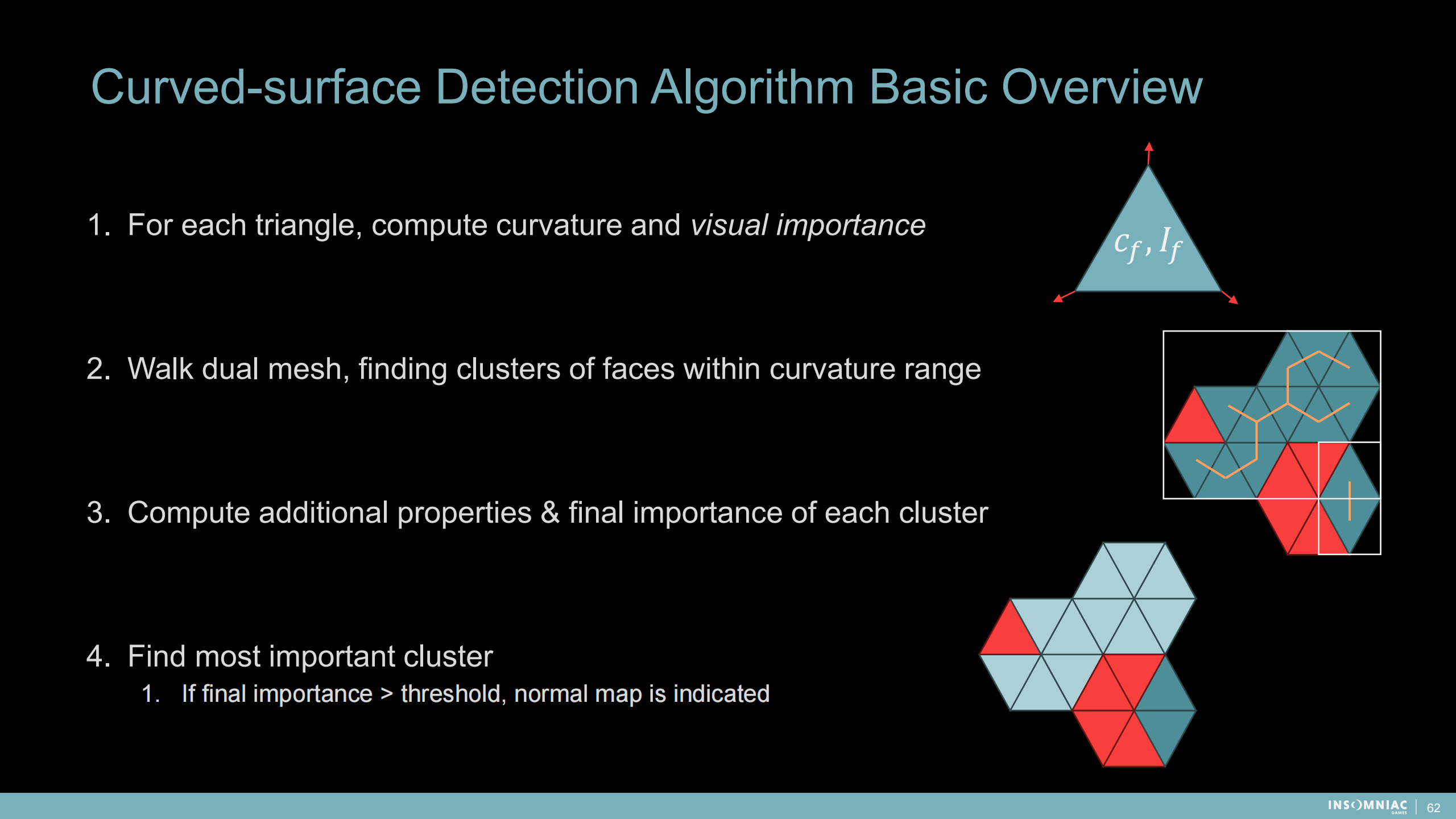
曲面探測算法基本概述

對每個三角面，計算曲率和視覺重要程度
遍歷網格，找到符合曲率範圍的面集群
計算每個集群的額外屬性和最終重要性
找到最重要的集群——如果最終重要度大於閾值，則分配法線貼圖

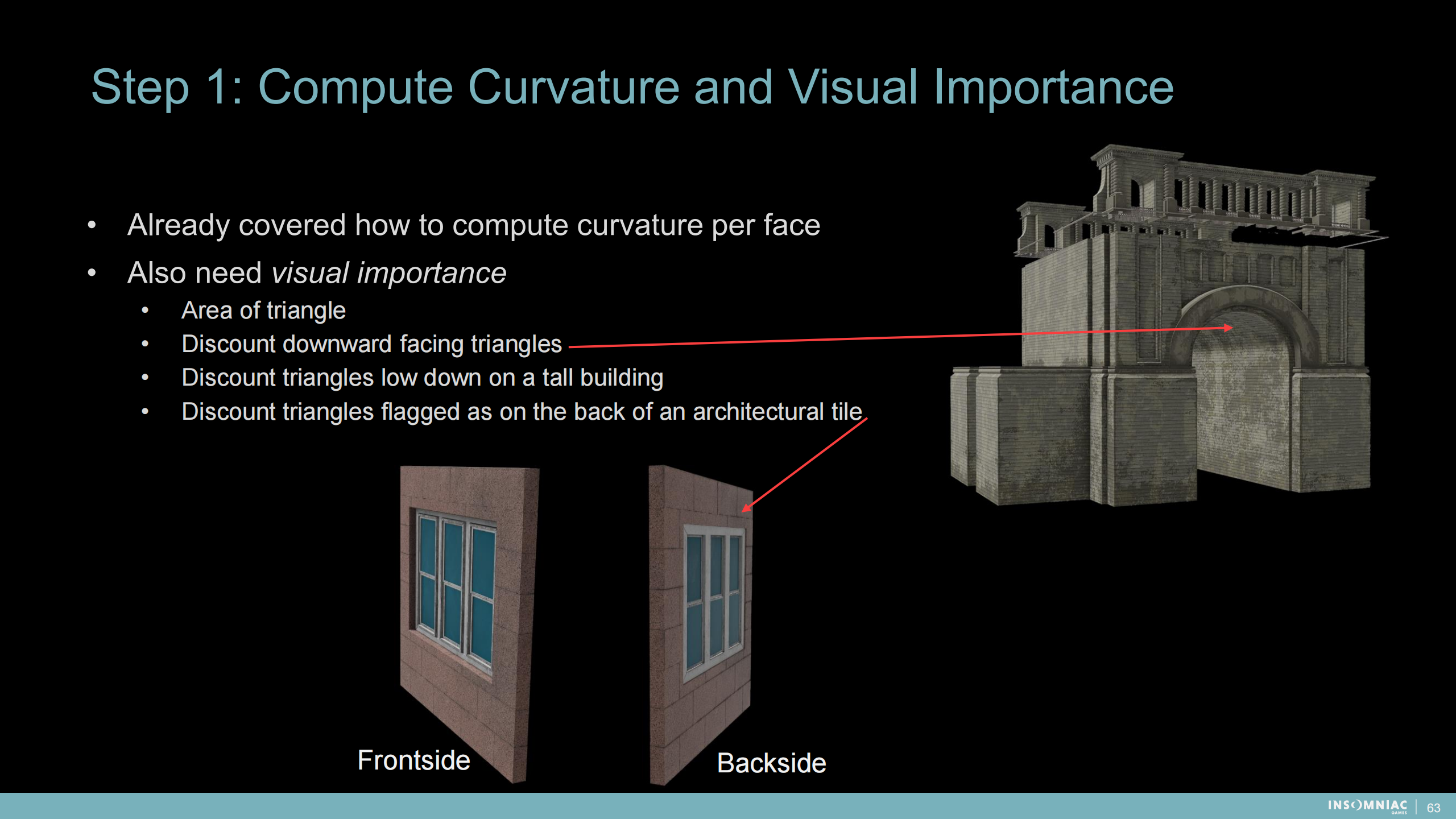
步驟1：計算曲率和視覺重要程度

——每個面的曲率如何計算已經介紹了

——還需要視覺重要程度

（基於）三角面積
低估朝下的三角面
低估大樓上較低部分的三角面
低估建築塊背面的三角面

步驟2：符合曲率範圍的面集群

低曲率的面通常很“平”
高曲率的面通常很“細緻”（意味著也不需要法線貼圖）
僅關注適當曲率的面——我們的範圍[1/128，4]（單位：米）
遍歷網格創建集群——僅跨越角落法線是可連續的邊（如圖）

步驟3：計算每個集群的最終重要性

——計算每個集群的額外屬性

總視覺重要程度
總表面積
包圍盒

——計算最終重要程度

視覺重要程度
低估和曲率半徑相比相對小的集群
低估非緊湊的集群——和總包圍盒相比表面積相對小的集群
低估有著過大或過小包圍盒的集群

步驟4：找到最重要的集群

——圖中綠色的集群是最高重要度的集群

——如果重要度大於閾值，則為其生成法線貼圖——圖中的建築經過自動探測，得出需要一個法線貼圖的結論

——對於《超凡蜘蛛俠2》

12%的遠距離LOD物體有大於0的重要度
在實踐中，我們通過調整閾值來自動識別出其中的5%
通過人工標註出剩下約5%——通常不總是因為曲率計算的原因

結語

後面還有兩節是自動化構建和運行時整合的概述，以及性能總結，由於篇幅原因這裡略去了。有興趣的可以直接去資料鏈接的原文看看。

（完成後的）整合的視覺呈現

這篇分享最吸引我的地方在於，在3A項目浩瀚的美術資產庫中，敢於和最終做到了以實現視覺提升為目的開發的一整套工具體系——3D項目的優化從來不僅限於運行時，很多時候都是從美術資產的加工就開始了。可以想象，這麼大規模的城市，如果不經過自動化而是以人工來加工，這是不可能完成的任務。

或許從玩家“純玩”的角度來說，這些都對玩不提供任何加成。但視覺體驗又從來不是一個可妙手偶得的過程，而是需要一個團隊一起踏踏實實積累和研發的。

反過來說，這個項目中其實他們也只有一次試錯機會，如果方案失敗了那麼畫面就無法升級，或者有視覺錯誤，或者性能表現堪憂。實際上也不是所有3A項目都能優化成功，很多確實是以優化失敗的狀態上線了，這也是3A項目越來越大的一項風險——只有這種規模的項目能提供優化經驗，但一旦失敗可能項目就沒了。

最後是資料鏈接：

Applied Mesh Analysis: Automating Distant City LODs in Marvel’s Spider-Man 2 GDC Vault

關於離散曲率的一篇paper