前言

《超凡蜘蛛侠2》这游戏我虽然没玩过，不过在大楼之间摆荡的画面确实很深入人心——在各个角度来说这个系列都是第一方3A游戏的优等生。

这次粗读的分享来自Scott Kircher，是Insomniac的核心开发工程师和图形工程师。

这篇GDC分享吸引我的原因，除了精致的PPT外，还有就是这篇分享的干货密度之高。另一个次要的原因就是这游戏的规模之大，LOD资源无法由美术人员进行手动调整，因此逼迫了工程师尽全力想出一些办法来批量和动态优化建筑网格，最终得出了不错的结果。

*由于资料没有解说稿只有PPT页，因此还是以翻译PPT页内容为主，补充一些我个人的说明。补充说明的内容会标星号。

1 面临的问题介绍

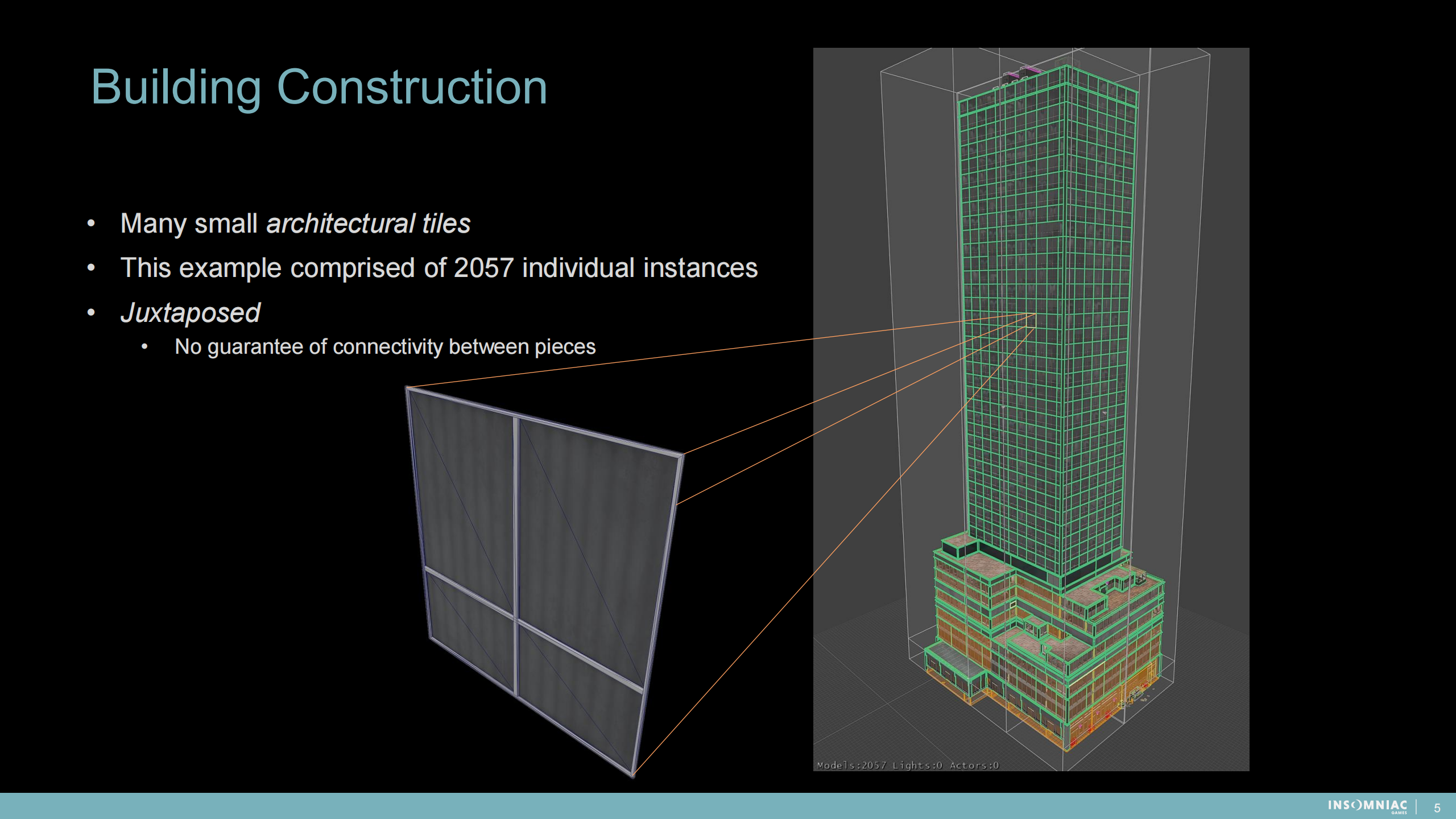
建筑结构

许多小的建筑块（tiles——瓦片形式拼接的）
这个例子中包含了2057个独立的实例
并置的——块与块之间没有连接

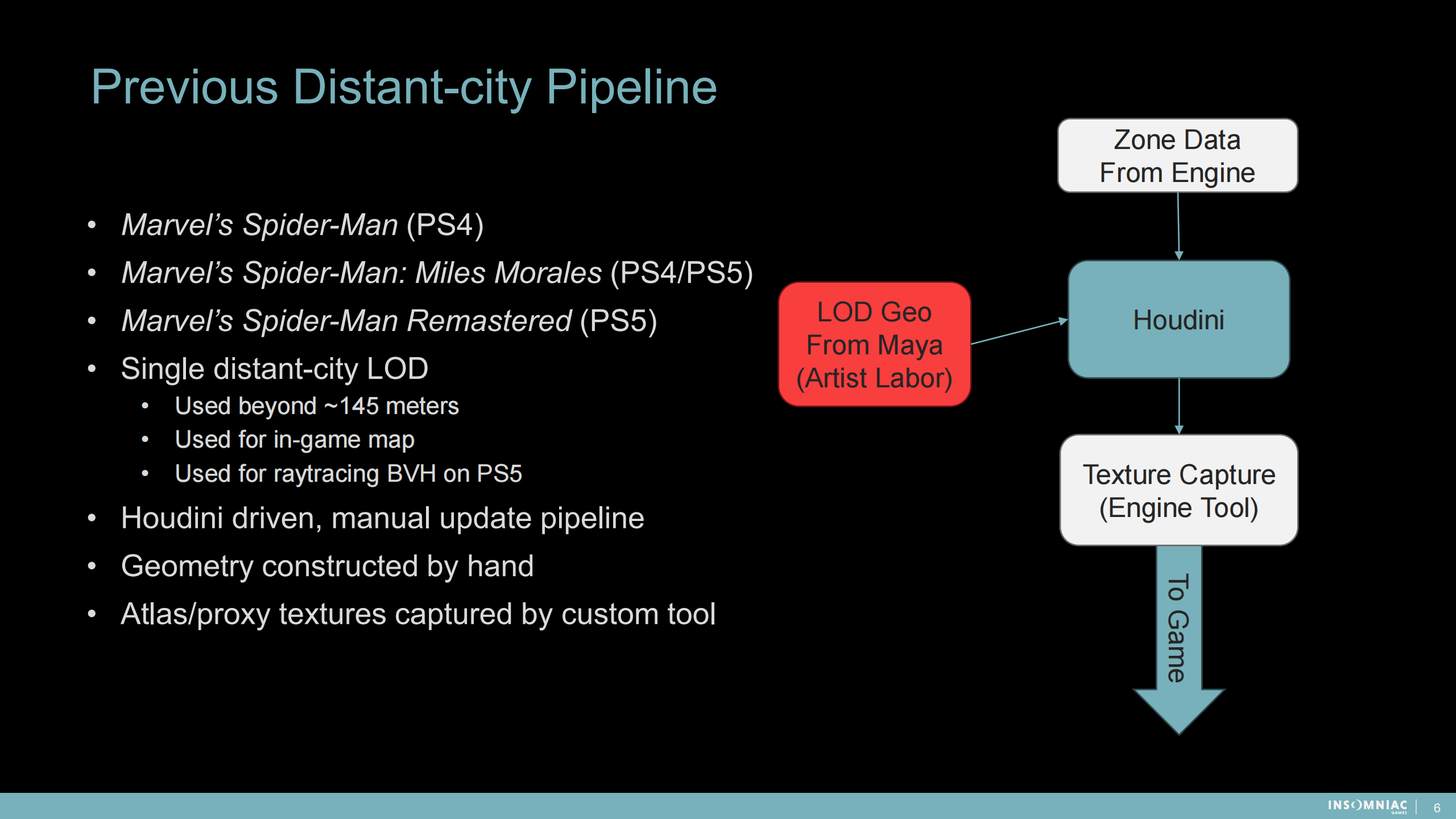
之前的远距离城市管线

*前几作游戏名不翻译了

单一的远距离的城市LOD：在超过145米时使用；在游戏内地图使用；作为PS5的光追BVH结构。
Houdini驱动，手动更新的管线（Houdini是较新的一款3D建模软件）
手动构建几何体
通过自定义工具收集图集和替代纹理

*关于BVH是一种空间加速结构，之前有文章介绍过。

新管线的目标

1）自动化

减少手工劳动
不再引入更多手工几何结构
通过构建服务器自动更新LOD（这个是构建工具链的概念，不是运行时的server）

2）提升质量

两层主要LOD：高密度、中等距离；低密度、远距离。
两层光追的BVH LOD：中等密度、中等距离；低密度、远距离。

重大的工程限制

1）游戏已经几乎完成了

产品还剩大约一年半时间
建筑的结构几乎已经完成了

2）16位索引格式

每个建筑最大65535个顶点（2的16次方）
适配已有的游戏系统并节省内存
尽量不要重构很多不熟悉的代码

3）内存、磁盘空间的紧缺

——顶点格式：每个顶点4字节

10位的压缩后的坐标
没有顶点法线或UV

——法线贴图需要被节俭地使用

节省内存
仅表现曲面时需要，避免其它情况

*整体来说，就是在工期有限、性能空间有限的情况下，需要把一层LOD想方设法调整成2层LOD，以提升画质并为光线追踪提供BVH数据。

2 网格简化——及带来的问题

通过Simplygon减少网格数

——已经购买了SImplygon的授权

用于常规（非距离化）的LOD

——通过网格减少工具反复简化网格

需要焊接步骤
（适用于）相似的几何与拓扑结构
对于非流形结构没有帮助（non-manifoldness 特指有多个面共享一个边的网格）
构成了每个建筑最初的距离LOD

通过Simplygon重构网格

——网格重构生成了完全新的网格

类似的几何结构
无关的连接性或拓扑结构
消除了非流形的边缘
可能非常昂贵——高密度的输出可能需要好几个小时
每个建筑需要生成次一级距离的LOD——加上生成BVH，工作量又加倍了

重构网格+网格减面的超级混合方案

——为我们提供了建筑结构

减少网格工具对于较高密度LOD工作良好
重构网格工具对于低密度LOD工作良好
两者之间如何呢？

——第一级远距离城市BVH LOD（中等质量和密度的）

平衡质量和内存
需要“中等的”密度
减少网格工具会打散并置的建筑块
重构网格工具的结果不太对：偏差太大、或是输出了太多顶点

——解决方案

对过分保守的目标物重构网格
然后（把网格）减少到需要的密度

那么，问题是什么呢？

——需要记得那些工程上的限制

建筑数据结构“不可修改”
16位
4字节顶点
尽量减少法线贴图的使用

——通过Simplygon的减少网格和重构网格工具是不够的

——三个主要问题

缺少法线信息
（被错误）网格重构的“内壳”
网格减少导致破皮、裂开问题

问题1：缺少法线信息

——顶点格式中仅包含位置（坐标）数据，没有法线数据

——（几乎）没有法线贴图

——法线是在运行时、逐三角面计算的（像旧的flat-shading一样）

——自动化的网格减少和重构会打乱表面结构

本来平整的结构会不再平整
看起来有镶嵌感
“三角定位故障”

*很多都是自动减面工具的一些常规问题，这类工具很难理想地处理结构稍微复杂的网格体。

问题2：网格重构的“内壳”

——（原本的）建筑结构通常会显得“空洞”

通常都是未封闭的
包含一些并非实际开放的边界
一些建筑块包含背面结构

——重构后带来一个封闭的网格

建筑表面被错误折叠在“建筑内部”
这被称为“内壳”

——（这种额外多出的内壳）比较浪费性能

——会带来光追上的潜在问题

问题3：网格减少后的裂开、破皮

并置的结构块
建筑块可能有内部缝隙——未连接或内部有穿插的几何结构
缝合不能解决所有问题
减少网格可能带来顶点移动——带来一些视觉上的缝隙
会导致漏光问题

“额外的”问题

建筑结构基本避免了法线贴图的使用
对于曲面该如何处理？——法线贴图或至少顶点法线是需要的
对于上千个需要处理距离LOD的物体，能自动检测出需要法线贴图的物体么？

*这一段很细致的介绍了建筑这种看起来方方正正的网格结构体在使用自动化减面工具时遇到的各种问题。由于前面也介绍过，自动化处理的方案是必须执行的，所以后续他们对自动化处理后的网格需要逐一解决这些问题——这也是这篇分享干货的开始。

3 三角网格分析

几何结构连接性拓扑结构

——几何结构

表面的“形”
顶点的位置
可通过（顶点的）插值计算三角面上的位置

——连接性

顶点通过边连接
三角面由边构成

——拓扑结构

在连续的变形中表面具备的不变性
例如：一个表面有多少个洞
可以仅通过连接性（不通过几何结构）进行推导

流形网格

流形边缘——严格由两个面共享一条边
流形网格——所有边缘都是严格由两个面共享的

*配图中展示了流形和非流形的区别。Manifold一词更多表示“具有多样性的”，简化成专有名词后确实丢失了很多信息。

（结构的）属

——属是一个形体上“洞”的数量

并非所有洞都是由形体边缘产生
用来度量拓扑结构的“复杂度”

——欧拉示性数（公式）

可以被用来计算流形三角面网格的属

*这里摘一段对欧拉示性数简要的分析：

其中V代表顶点数，E代表边数，F代表面数。对于与球面同胚的多面体，欧拉示性数恒等于2。然而，并不是所有物体的欧拉示性数都为2，例如环面的欧拉示性数为0。

此外，欧拉示性数还可以通过公式2-2g来计算，其中g指的是闭可定向曲面的亏格数（即有多少个洞）。这个公式揭示了欧拉示性数与亏格数之间的关系。（上面则是一个反算过程）

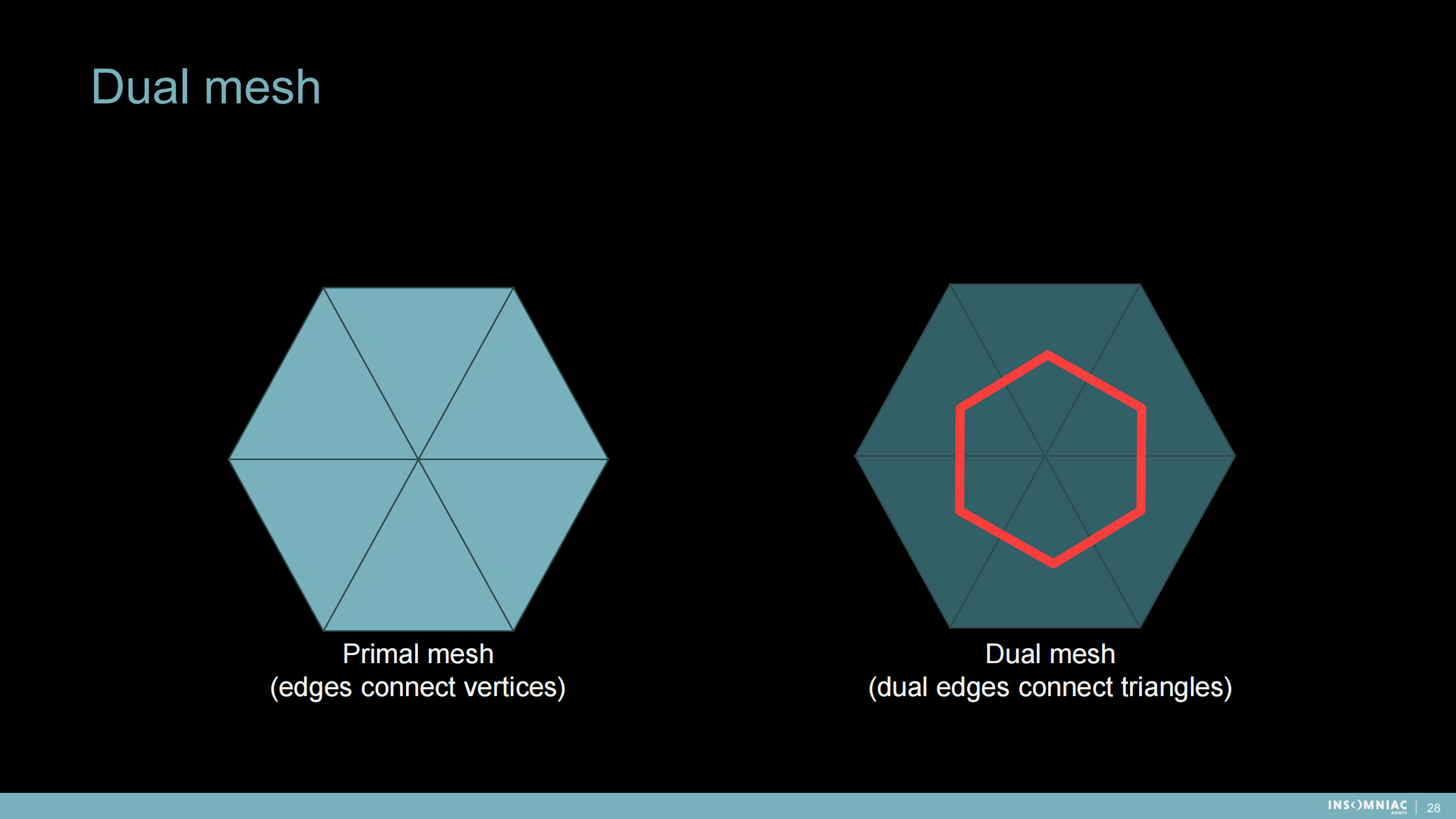
双重网格

*双重网格增加了一层边用来连接三角面的中心。

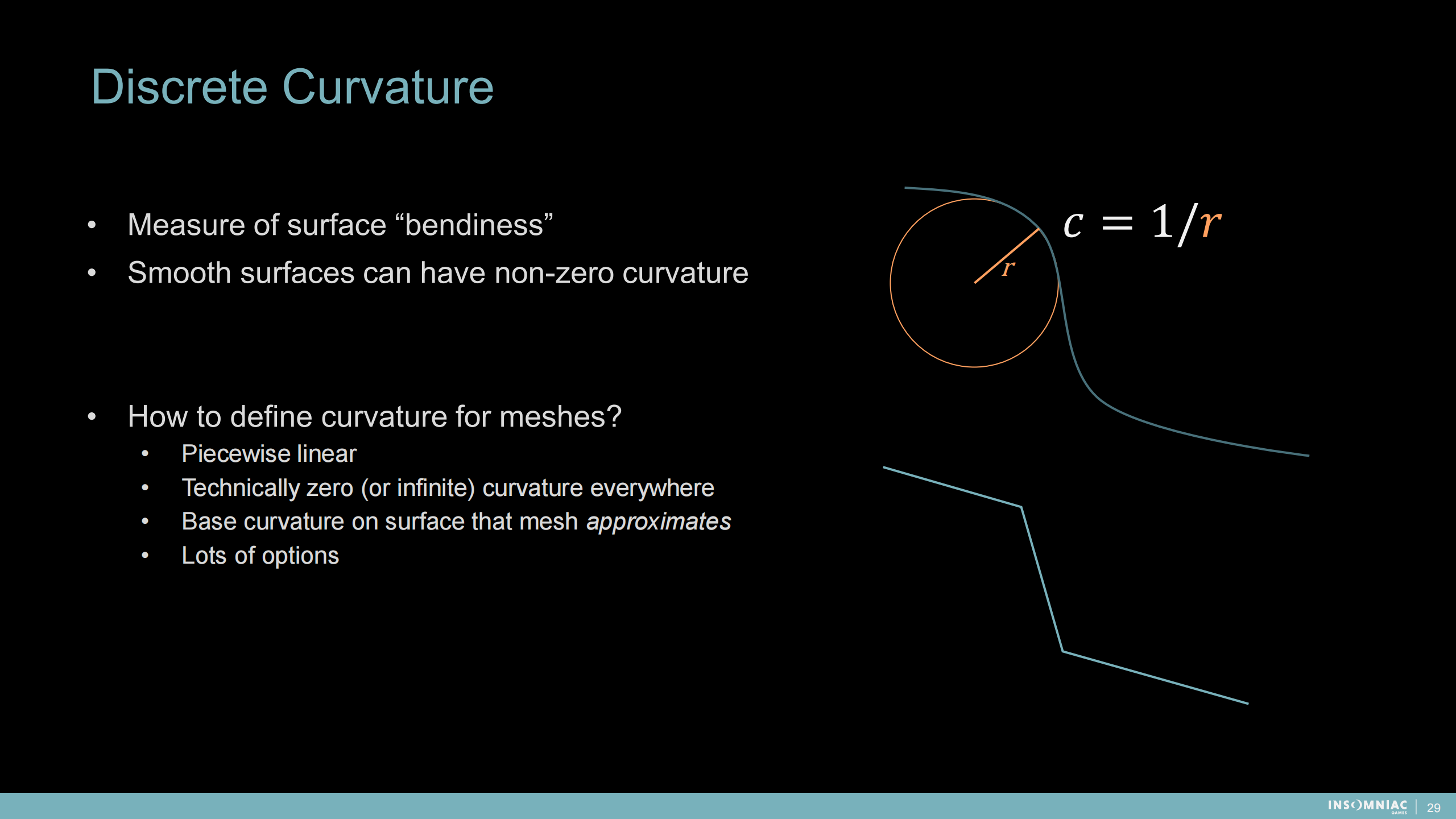
离散曲率

——用来度量表面的“弯曲度”

——平滑表面也可能有非零的曲率

——如何定义网格的曲率？

分段线性
各处有很多零（或无限）的曲率
表面的基础曲率可以作为网格的近似
有很多备选方案

*关于离散曲率是一个复杂课题，离散分段法只是一种基础的方式，更多推导方式我也没有能力全面介绍。文末会附一篇资料链接。

*这里介绍的这些数学工具主要就是用来解决之前提到的3+1个问题的。

4 网格平整

主要思想

——（整体的）光照着色比轮廓形体更重要

尤其对于远距离LOD
尤其对于本应是平整的表面

——在网格减少时保存法线信息

在Simplygon减面工具中提高法线权重
在后续导出时取消这一设置（最终结果是不包含顶点法线的）
可以帮助减少结果的偏差
仅靠这个工具自身是不足够的
对于重构网格则完全不适用

——核心思想：平整减面后的网格

修改几何体，使单独的三角面法线适配预期的法线方向

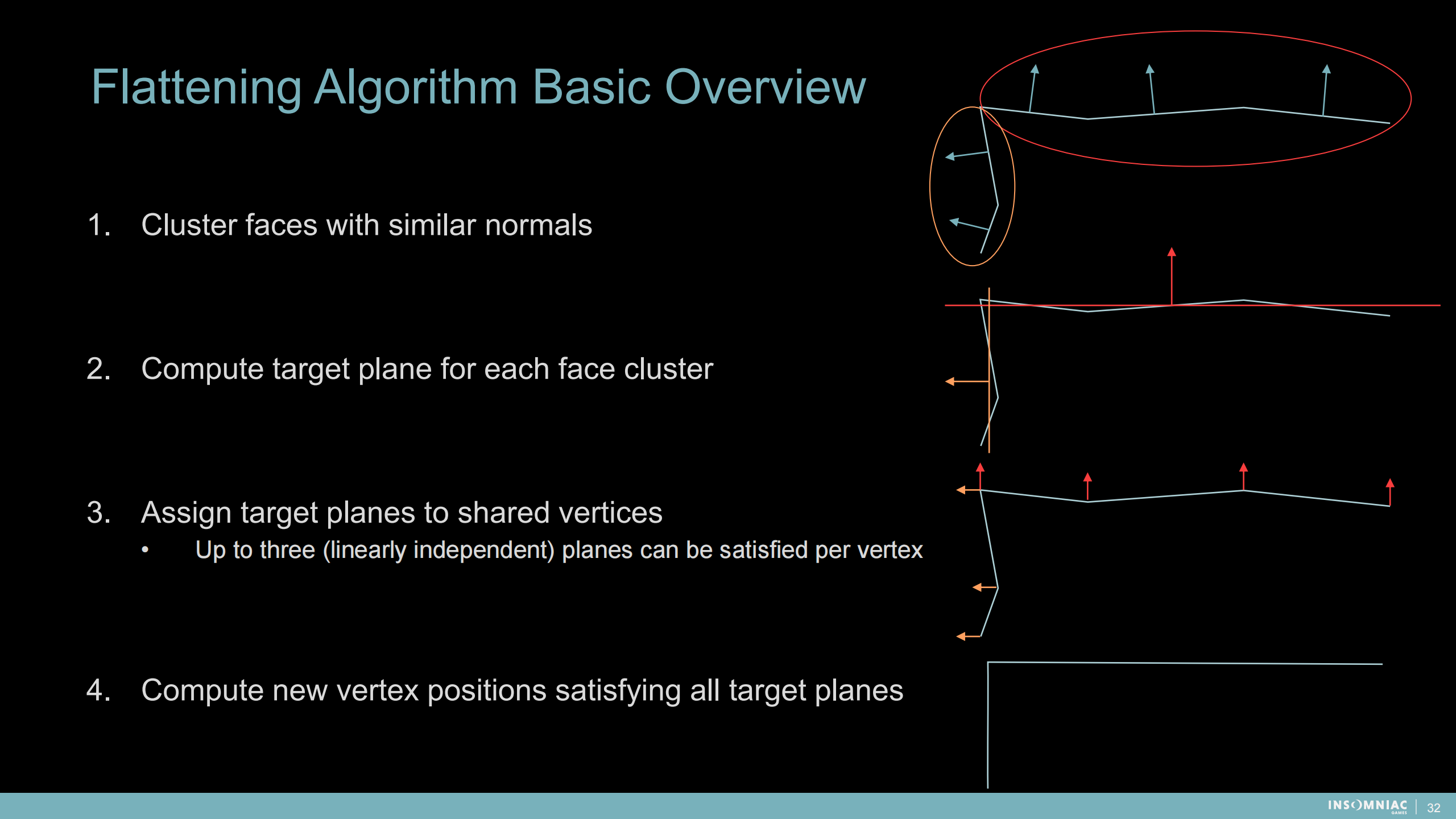
平整算法概述

将有相似法线的面集群化
对每个集群计算目标平面
将（平面位置和法线信息）分派到共享的顶点上——每个顶点满足最多三个（线性独立）的平面
计算满足所有新平面的顶点位置

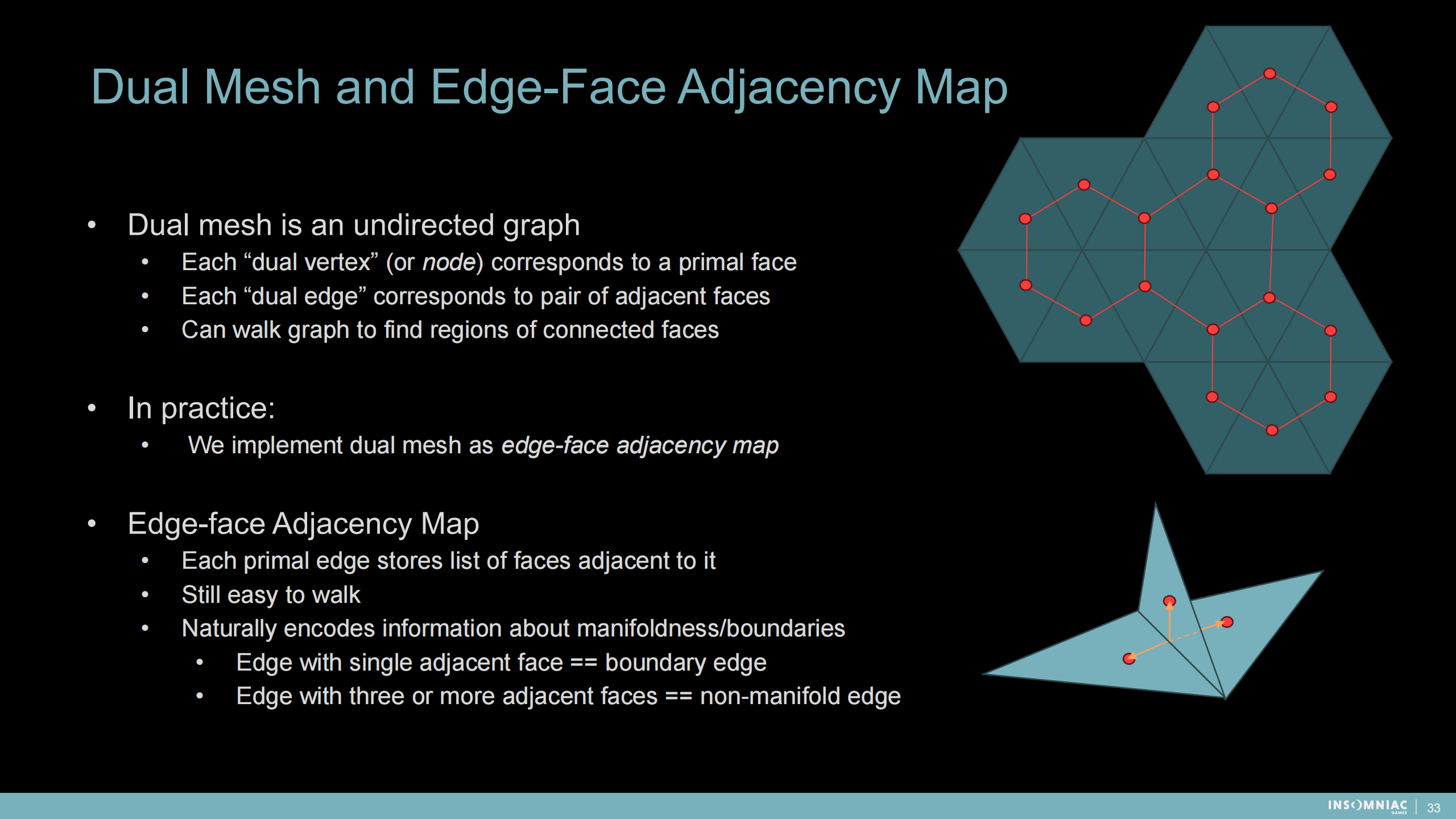
双重网格和边面连接图（这里图是一种数学结构）

——双重网格是一种无向图结构

每个“双重顶点”（或节点）对应一个三角面
每一个“双重边”对应一对连接的面
可以遍历图来查询面之间相连的区域

——在实际应用中，我们采用了边面连接图（作为数据结构）。

——边面连接图

每个原始边存储与之相连的面的列表
仍然易于遍历
可以自然地编码流形和边缘信息（通过连接数）：单独连接面的边——边缘边；连接三个或更多面的边——非流形边。

步骤1：将有近似法线的面划为一个集群

A. 选择下一个集群的种子面——（区域中）最大的为划入集群的面。

B. 遍历边面连接图（双重网格）

广度优先遍历
不访问和种子法线差距“太大”的面
这组访问到的面的集合构成了新集群

C. 如果存在未访问的面，重复步骤A

面的法线相似度

比较面的法线——始终和种子面进行比较（前述选择用来开启新集群的面）
对于网格减少的结果——可以使用（减面过程保存的）原顶点的法线数据；可以得到和原始网格很接近的着色结果
对于网格重构的结果——直接使用计算后的表面法线

步骤2：为每个面集群计算目标平面

直接计算集群区域内的各面的平均值（逐集群）。
可以对集群内的点做最小平方拟合——非必须，因为集群在其结构上已经是“最平方案”了。

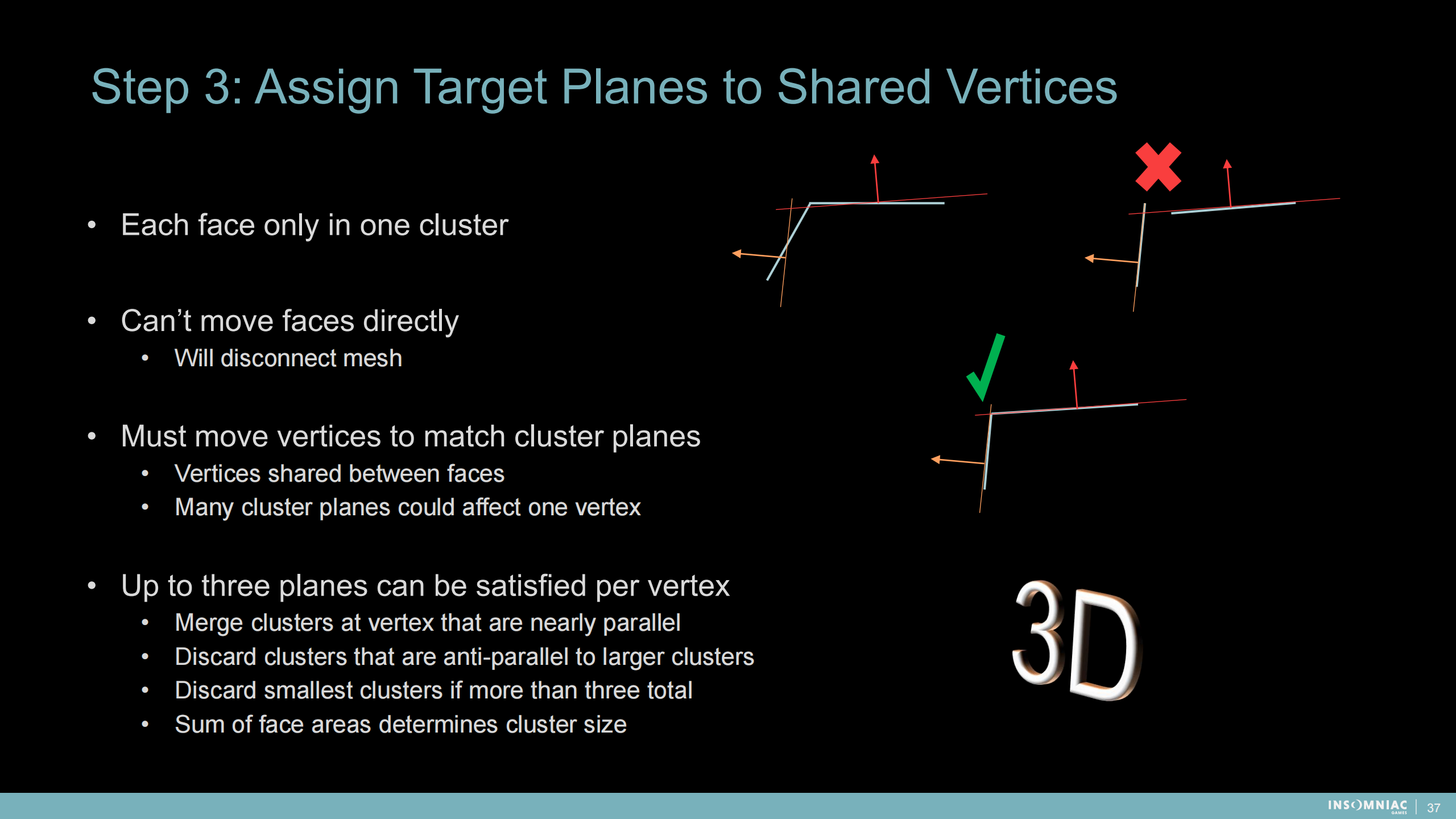
步骤3：分配平面属性到共享的顶点

——每一个面只属于一个集群

——不能直接移除这些面——会带来不连接的网格

——必须移动顶点来适配集群平面

顶点可能被多个面共享
多个集群平面可能影响同一个顶点

——每个顶点最多满足3个平面

顶点处的合并集群是集合平行的
取消（顶点处）与大的集群不平行的小集群
取消（顶点处）大于3的小集群
集群的大小用内含的面的个数来计算

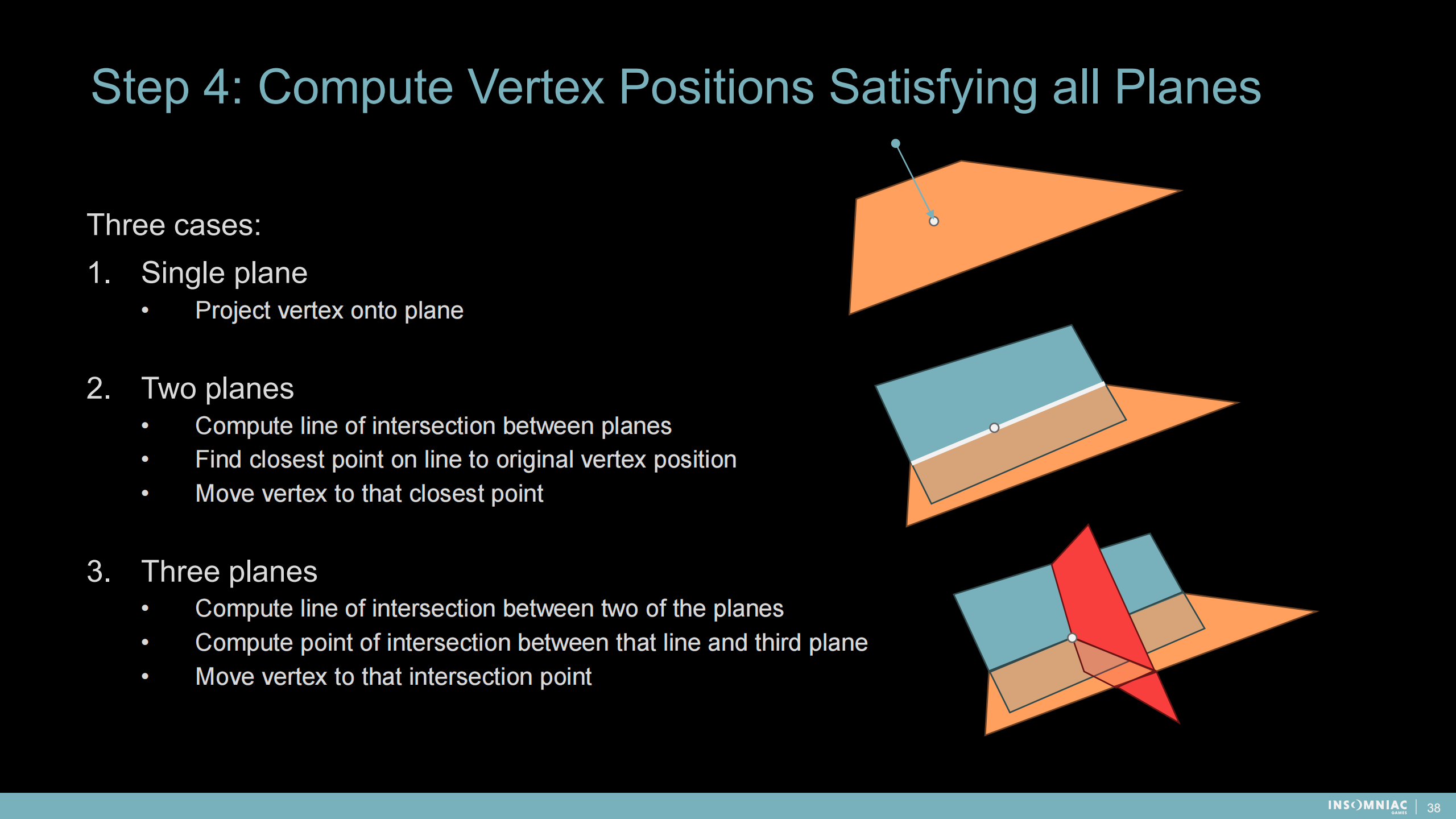
步骤4：计算满足所有相关平面的顶点位置

三种情况：

1）单平面——把顶点投影到平面

2）双平面——计算平面的相交线；找到顶点位置到线上最近的点（投影到线）；移动顶点到那个最近的点

3）三平面

计算任意两平面的相交线
计算线与第三平面的交点
把顶点移到该点位置

平整后的结果

5 内部结构分类——解决“内壳”问题

核心思想

粗略地将面分为内部和外部
局部信息是不足够的——对凹面形体来说法线方向是没意义的
需要一些全局信息（仍然很难）
使用“泛滥填充”（遍历双重网格）来解决——目标：获得一个连接体内的内部面的连续集合。

内部结构分类基本算法

基于Stochastic射线检测方案（离线工具）

1）识别出少量的内部点

用蒙特卡洛采样的方式，在包围盒的水平展开的范围内采样

2）内部面集合的分类

从每个内部点，对每个面发出射线
检测每个面是否能“看到”该内部点（基础计算可以去看Games101）

3）最终进行泛滥填充

生成一组相连的内部面的单一集合
（以及一组外部面的集合）

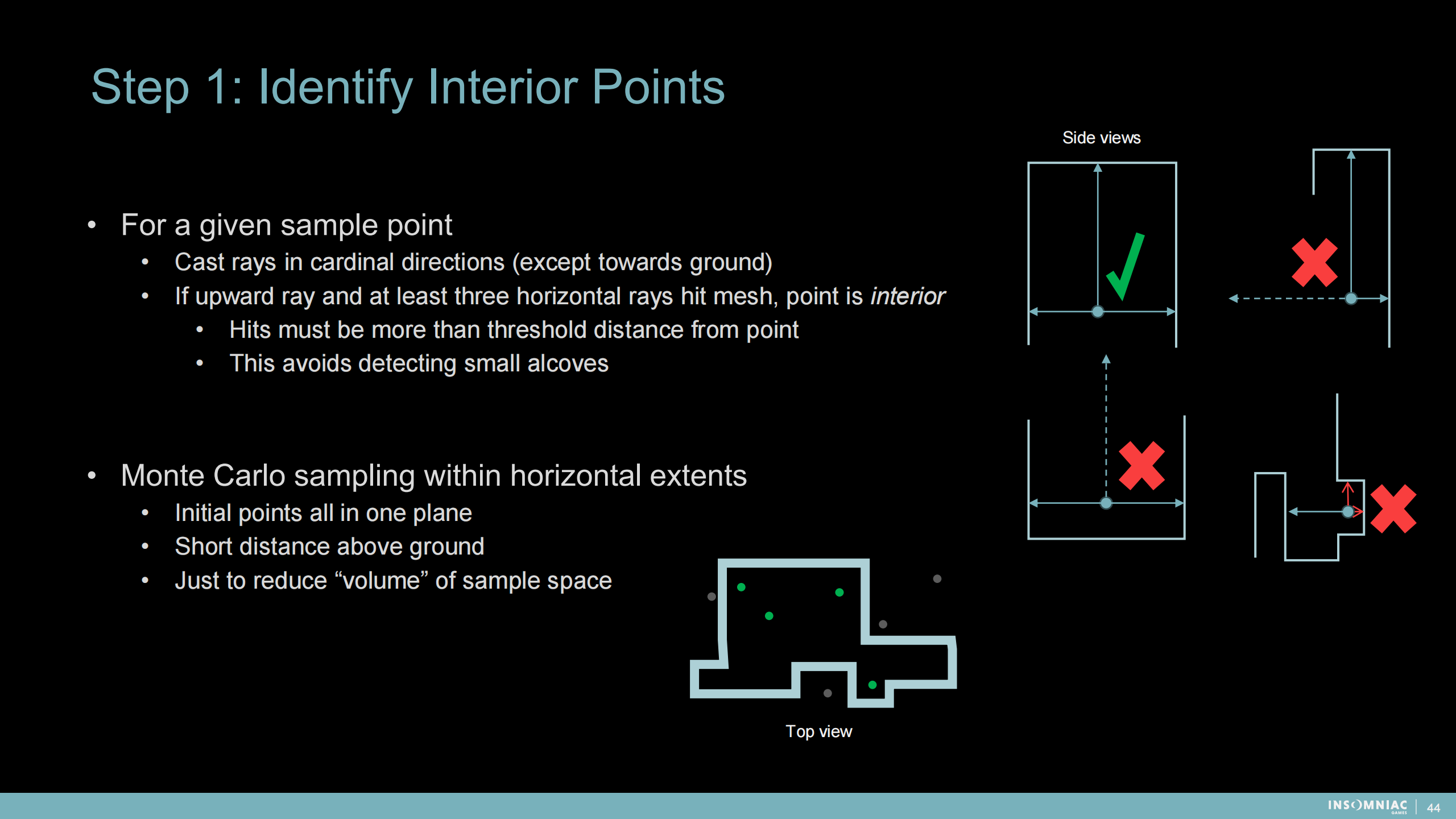
步骤1：识别内部点

1）对于一个给定的采样点：

对基本的方向（可以理解成轴向的）发出射线——地面方向除外。

如果向上的射线和至少3根水平射线命中了网格，则点是内部点。

命中位置与起点距离必须大于距离阈值
这可以避免检测出小的壁凹

2）水平展开的蒙特卡洛采样：

所有初始点都在一个平面内
在地面上方一小段距离
目的是减少采样空间的“体积”

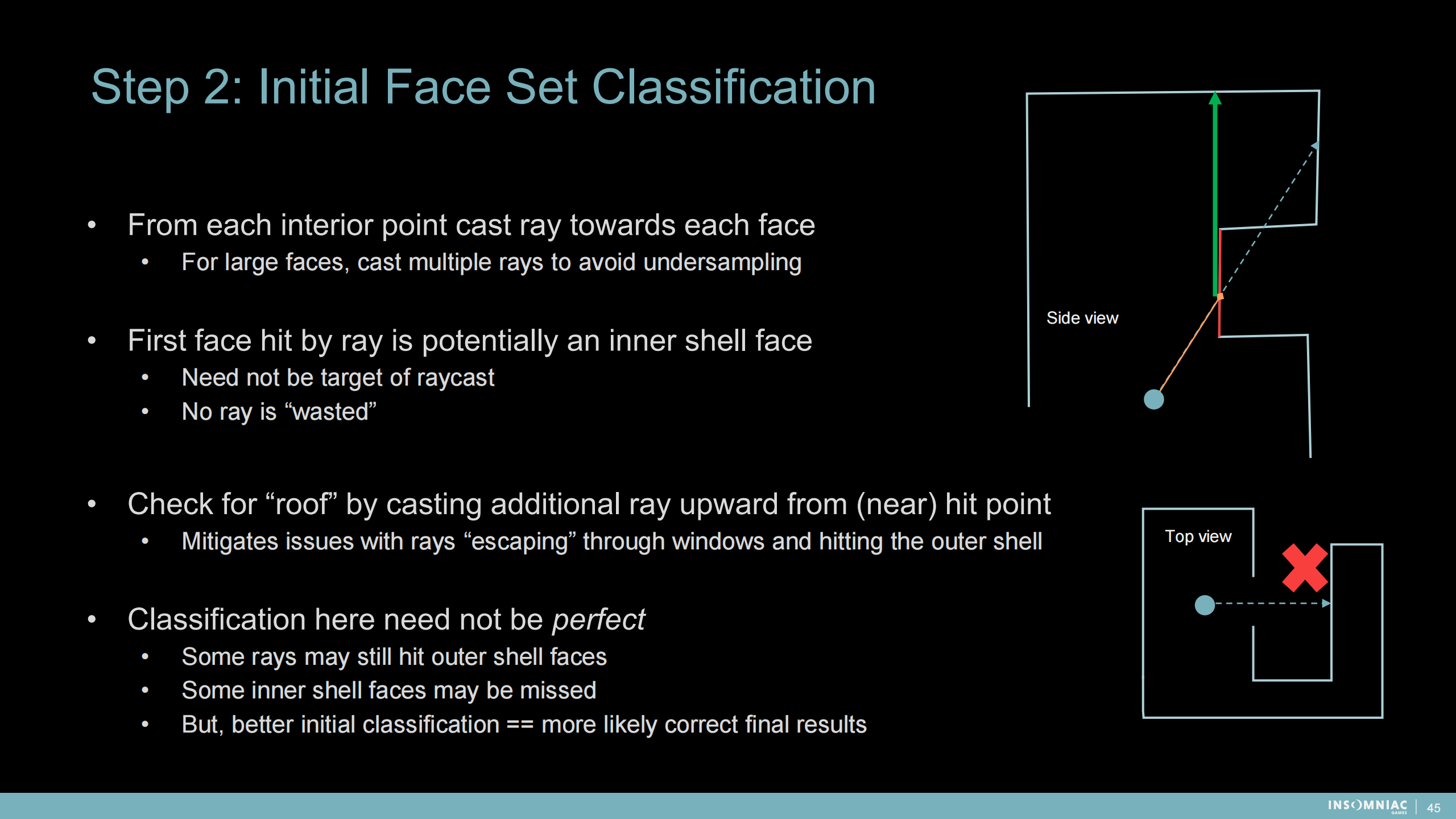
步骤2：内部面集合的分类

1）从每个内部点向每个面发出射线

对于大平面可以发出多条射线以避免采样不足

2）第一个命中的面是一个潜在的内壳面

需要将其不视为射线检测的目标
这样可以避免射线的“浪费”

3）通过从命中点（或附近）射出额外的向上射线来检测“房顶”

减少射线通过窗口位置“逃逸”并命中外壳的问题

4）这里的分类方式不需要是完美的

仍可能有部分射线命中外壳
可能漏掉一些内壳的面
不过，更好的初始分类就更接近正确的结果

步骤3：泛滥填充修正

从每个外壳面遍历双重网格

只遍历至其它外壳面
找到外壳面的连续集

步骤3：泛滥填充修正

保留最大的外壳面集合——将其它的标注为内壳
重复处理内壳面——找到内壳面的连续集

步骤3：泛滥填充修正

保留最大的内壳面集合——将其它的标记为外壳。
现在我们找到了一个单一的连续内壳

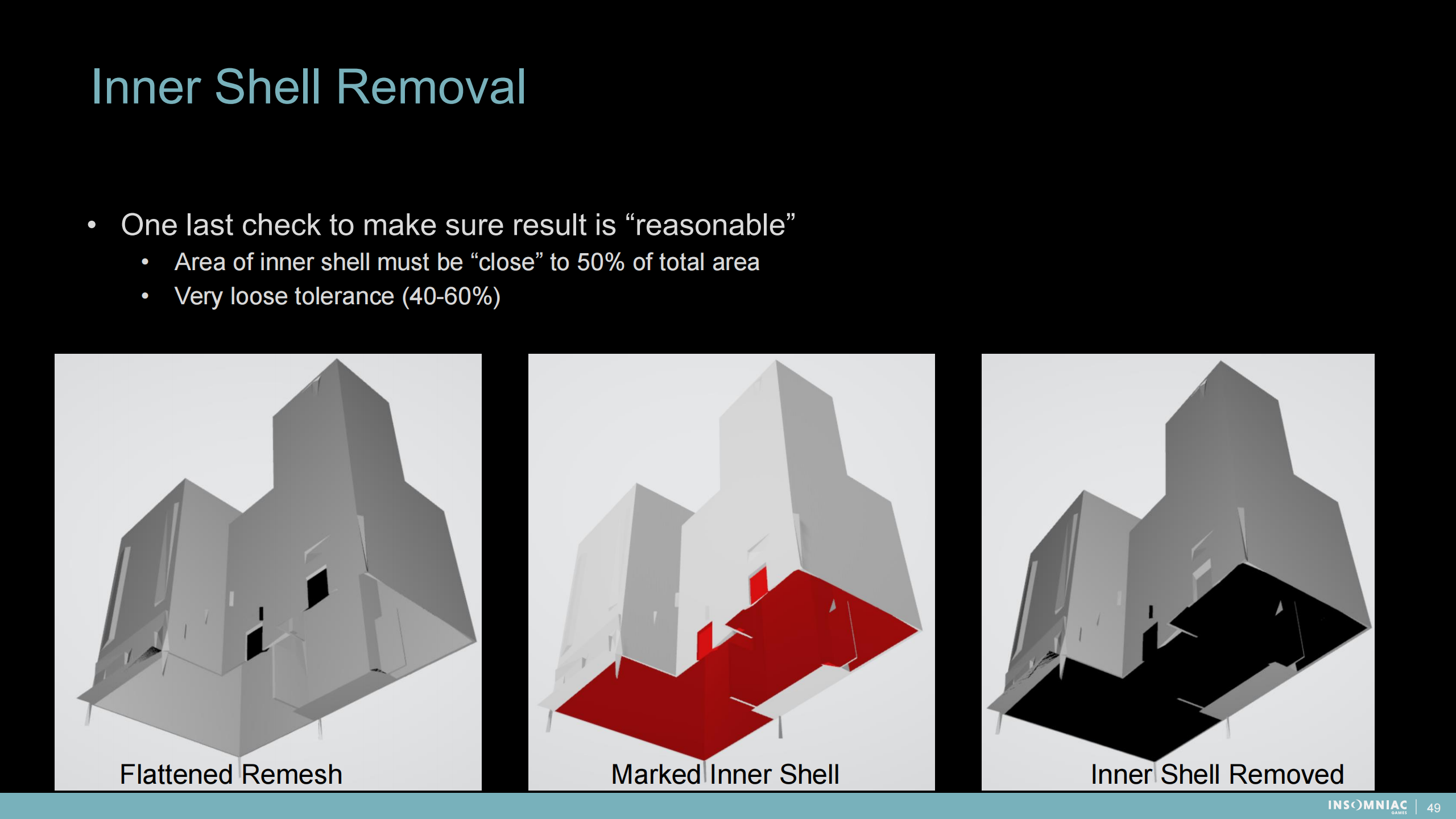
“内壳”移除

最终检查步骤以保证结果是“合理的”：

内壳区域必须“接近”50%总区域范围
可以有比较松散的容差空间（40-60%）

*通过移除之前工具生成的“内壳”，可以减少大量不可视网格的渲染计算，最终提升性能。

6 生成支撑物——解决网格裂开问题

核心思想

必须移除网格减少导致的裂开问题——消除漏光（影）问题
观察：网格重构后的内壳能较好适配原始网格的内部——并且，它是一个单一连续无破皮的体块

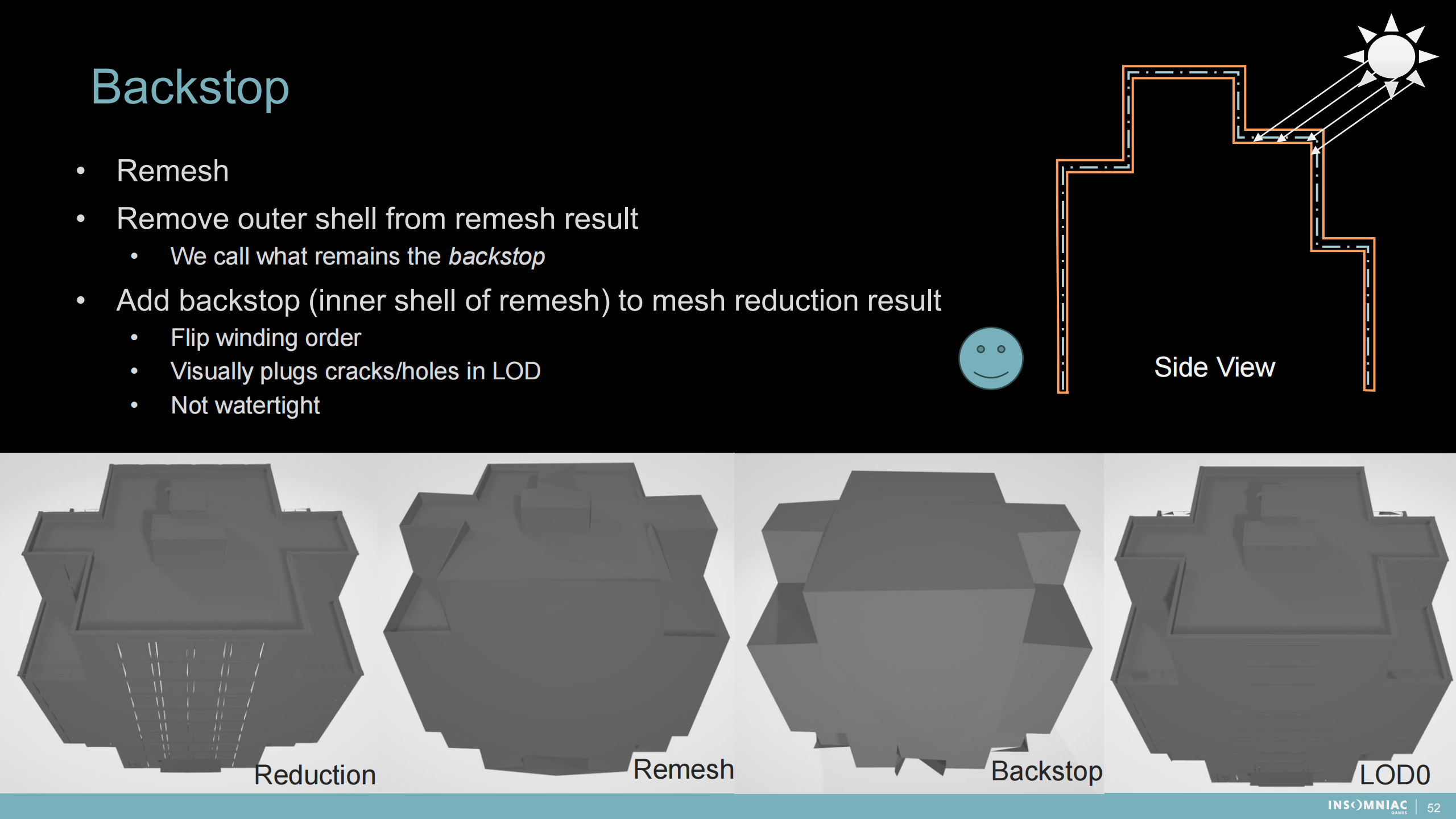
支撑物

*backstop有很多不贴合这种情况的翻译，支撑物只是相对合适的一个。

1）重构网格

2）移除重构结果的外壳——我们把余下的部分称为支撑物

3）将支撑物（内壳或重构后的网格）添加到网格重构后的结果中

翻转绕序
视觉上堵住LOD的裂开或洞
结果并不是天衣无缝的

*绕序翻转的作用是把本来向内的网格朝外。

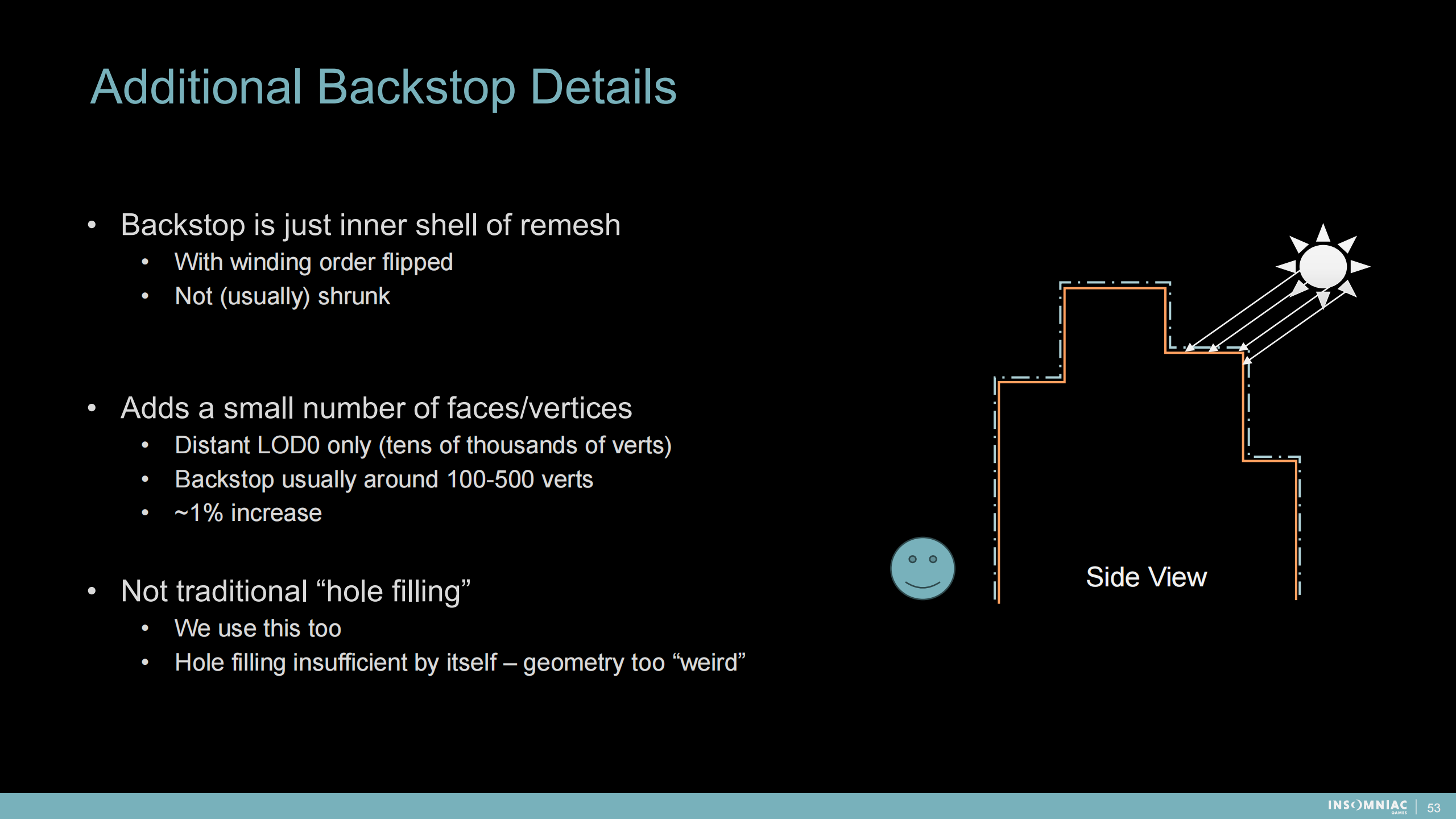
额外的支撑物细节

1）支撑物只是内壳或重构的网格

经过绕序翻转
（通常）不缩小

2）添加了少量的面或顶点

仅用于远距离LOD（成千上万的顶点）
支撑物通常在100-500顶点
整体约增加了1%

3）不是传统的“补洞”方案

我们也使用了传统补洞工具
补洞工具有其自身的不合适之处——补充的几何体结构过于“奇怪”了

支撑物后备方案

1）重构的网格内壳不是总存在

原始网格可能已经（几乎）完全封闭了

2）备选方案

将网格重构的结果沿着其法线方向轻微收缩
翻转背面

3）从轮廓上可能看到细边缘的视觉错误

所以，尽量还是使用内壳作为支撑物

不适合使用支撑物的建筑结构

城市中并非所有建筑都是大楼
支撑物不适合某些物体——有其是桥和类似的辅助结构

检查不适合使用支撑物的建筑结构

1）观察：桥或辅助结构通常有很多的“洞”

2）可以使用拓扑结构的属来自动探测

大楼建筑有相对低的属
桥有非常高的属

3）想要忽略轻微的裂开和非流形的情况

Simplygon网格重构带给我们没有“小”洞的流形网格
计算重构网格的属

4）同时使用一个表面区域阈值

大楼建筑应该有更大的表面区域
雕像或其它物体有更小的表面区域

5）艺术家可以强制覆盖（支撑物结果）

强制开启
强制关闭

7 自动探测法线贴图

核心思想

曲率分析
计算并估计一些视觉上明显的曲率——有着高视觉曲率的建筑需要有法线贴图；其它的，“大概”就不需要。

我们的离散曲率定义

直觉：原始网格表面的法线和表面的曲率相关
曲率和表面切线所在圆的半径反相关
考虑面上的一条边（如图）

*图中是一些向量计算，包括后面整个方案基本也是向量级别的计算。

面的曲率和面的集群

我们关注于一个网格区域的“总”曲率数值
以边长权重作为边曲率的平均值，来估计面的曲率（直接看公式即可）
以面积权重作为面曲率的平均值，来估计面集群的曲率

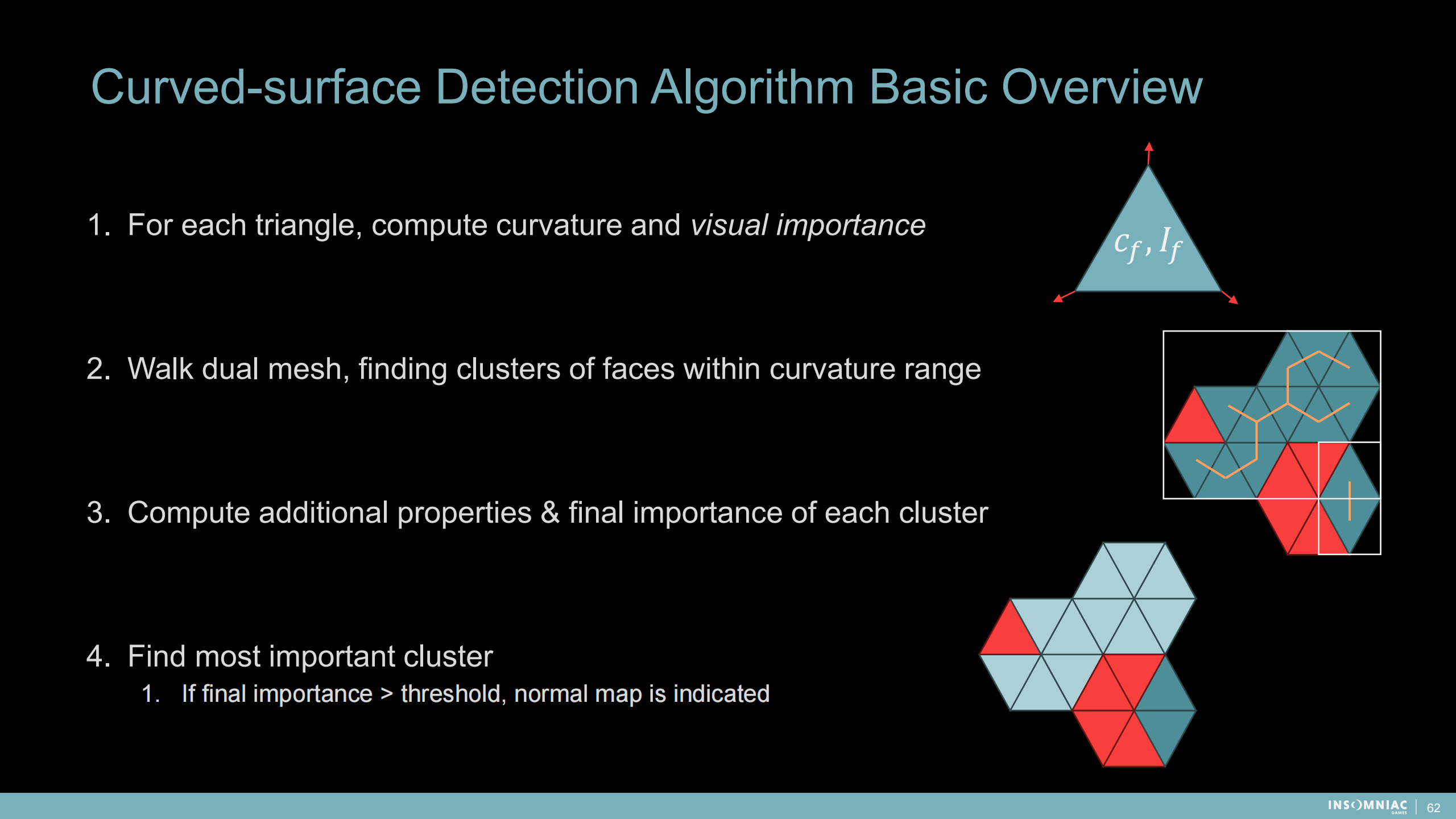
曲面探测算法基本概述

对每个三角面，计算曲率和视觉重要程度
遍历网格，找到符合曲率范围的面集群
计算每个集群的额外属性和最终重要性
找到最重要的集群——如果最终重要度大于阈值，则分配法线贴图

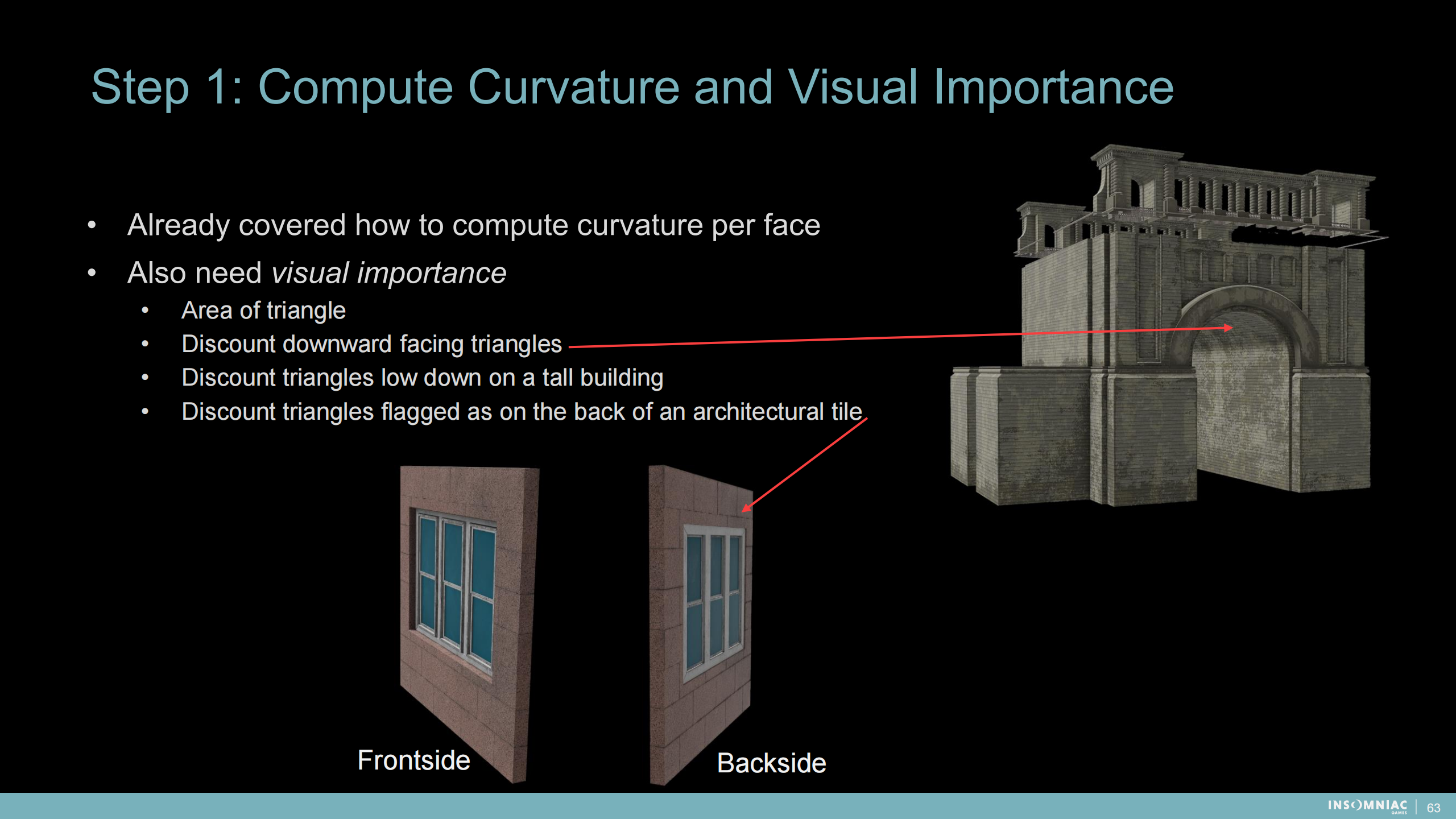
步骤1：计算曲率和视觉重要程度

——每个面的曲率如何计算已经介绍了

——还需要视觉重要程度

（基于）三角面积
低估朝下的三角面
低估大楼上较低部分的三角面
低估建筑块背面的三角面

步骤2：符合曲率范围的面集群

低曲率的面通常很“平”
高曲率的面通常很“细致”（意味着也不需要法线贴图）
仅关注适当曲率的面——我们的范围[1/128，4]（单位：米）
遍历网格创建集群——仅跨越角落法线是可连续的边（如图）

步骤3：计算每个集群的最终重要性

——计算每个集群的额外属性

总视觉重要程度
总表面积
包围盒

——计算最终重要程度

视觉重要程度
低估和曲率半径相比相对小的集群
低估非紧凑的集群——和总包围盒相比表面积相对小的集群
低估有着过大或过小包围盒的集群

步骤4：找到最重要的集群

——图中绿色的集群是最高重要度的集群

——如果重要度大于阈值，则为其生成法线贴图——图中的建筑经过自动探测，得出需要一个法线贴图的结论

——对于《超凡蜘蛛侠2》

12%的远距离LOD物体有大于0的重要度
在实践中，我们通过调整阈值来自动识别出其中的5%
通过人工标注出剩下约5%——通常不总是因为曲率计算的原因

结语

后面还有两节是自动化构建和运行时整合的概述，以及性能总结，由于篇幅原因这里略去了。有兴趣的可以直接去资料链接的原文看看。

（完成后的）整合的视觉呈现

这篇分享最吸引我的地方在于，在3A项目浩瀚的美术资产库中，敢于和最终做到了以实现视觉提升为目的开发的一整套工具体系——3D项目的优化从来不仅限于运行时，很多时候都是从美术资产的加工就开始了。可以想象，这么大规模的城市，如果不经过自动化而是以人工来加工，这是不可能完成的任务。

或许从玩家“纯玩”的角度来说，这些都对玩不提供任何加成。但视觉体验又从来不是一个可妙手偶得的过程，而是需要一个团队一起踏踏实实积累和研发的。

反过来说，这个项目中其实他们也只有一次试错机会，如果方案失败了那么画面就无法升级，或者有视觉错误，或者性能表现堪忧。实际上也不是所有3A项目都能优化成功，很多确实是以优化失败的状态上线了，这也是3A项目越来越大的一项风险——只有这种规模的项目能提供优化经验，但一旦失败可能项目就没了。

最后是资料链接：

Applied Mesh Analysis: Automating Distant City LODs in Marvel’s Spider-Man 2 GDC Vault

关于离散曲率的一篇paper