計算條件是：每一抽概率0.006，若連續89抽沒出，則下一次必出，出貨後重新計算保底。
這裡有兩種計算方法。第一種是吧友 天意 貢獻的'第一黃平均抽數'計算法（但是他算錯了-_-||）。第二種是我自己想的'無限抽構造法'。兩種方法完全不同，結果完全一致，可以互相印證。
'第一黃平均抽數'計算法：
考慮到90抽保底，所以只計算90抽的情況。
分情況計算，89抽0黃至89黃的情況分別計算。
0黃，觸發保底，概率0.994^89，第一黃平均抽數90。
1黃，無保底，概率（C1/89）*（0.994^88）*（0.006^1），第一黃平均抽數90/2。
2黃，無保底，概率（C2/89）*（0.994^87）*（0.006^2），第一黃平均抽數90/3。
……以此類推至89黃。
計算出每個平均抽數的概率，再加權合計即可得綜合平均抽數，最後取倒數即可得綜合概率。
手算顯然不現實，所以藉助於Excel
因為89抽10黃以上概率太小，所以後面都略了。綜合概率1.43%
'無限抽構造法'
假設我是米哈遊的爸爸，所以我可以無限抽ԅ(¯ㅂ¯ԅ)
無限抽n次，n=>∞ 此時沒有保底先抽，則出貨0.006n，然後根據保底規則將其中的3-4星替換為5星。那麼要替換多少呢？
令k=0.994^90，任取一黃的位置開始模擬抽卡，距離下一黃的距離有幾率k大於90，有幾率k^2大於180，有幾率k^3大於270……以此類推至k^∞。
那麼根據保底規則，任意一黃之後平均應該替換（k+k^2…+k^∞）個3-4星為5星。此時，出貨分佈符合題設條件。
兩者相加得總出貨數，根據概率的基本定義，總出貨除以總數n得概率。
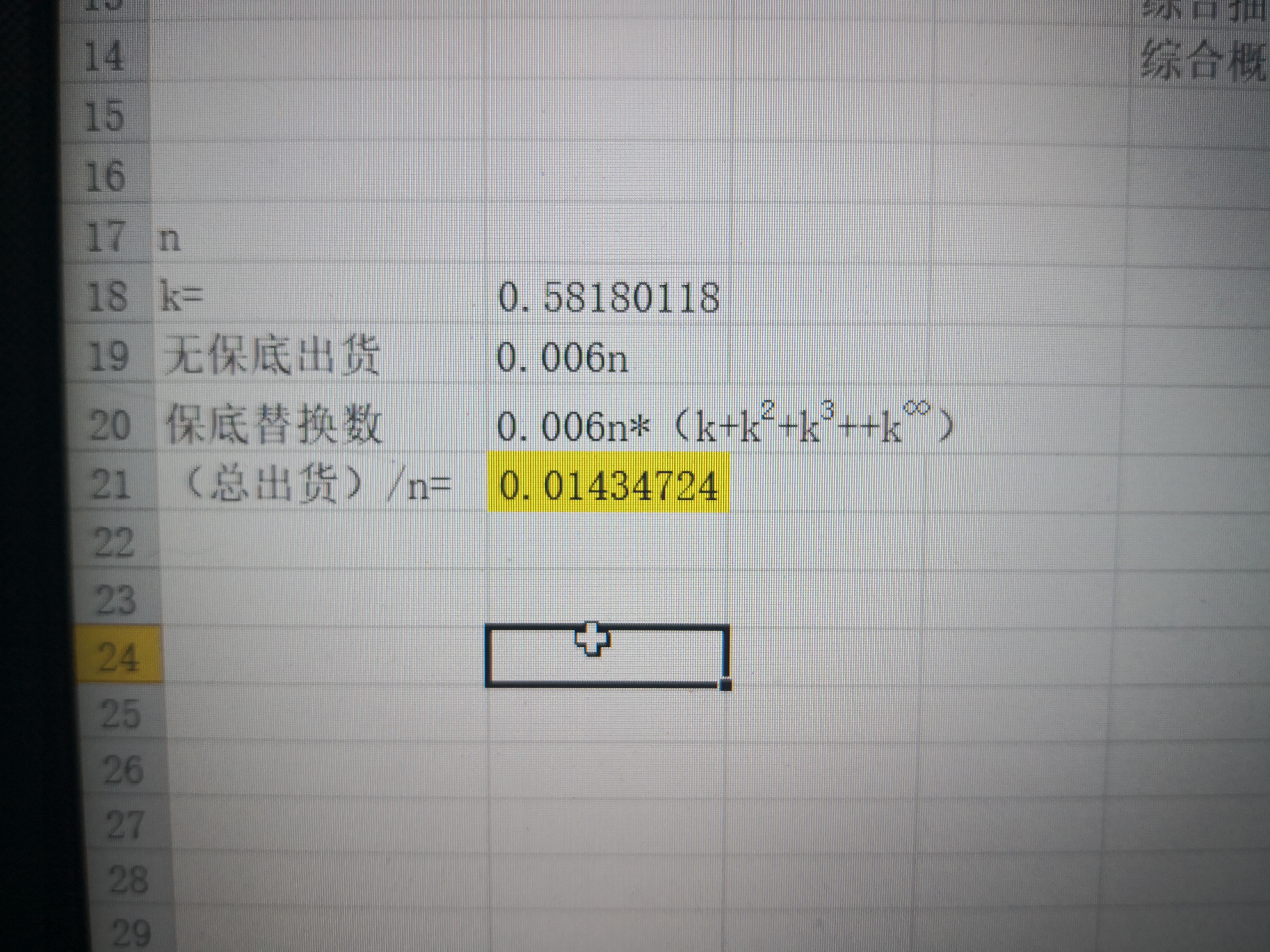這個方法要想到需要一些基本功，但是計算簡單，手算即可。綜合概率1.43%偽隨機1.6%怎麼算的我也不知道_(:з)∠)_