前言

這周繼續讀三維重建方面的技術向課件。按照之前的大綱，這次讀到前AI時代中，計算機視覺方面的一項技術——

Structured Light（結構光）。這項技術作為立體視覺之後提出的一項技術，其理解跨度相對不算大。

簡單來說，這是一項用激光等光源投在物體表面、再用相機等設備進行採樣的技術，注重還原物體的三維結構。

介紹結構光的論文其實也很多，但作為個人能全部仔細讀完以及圖文搭配合適的內容，這次我選擇了UTAH於2015年的計算機視覺課件。和之前一篇比較長的PPT拆分成上下兩篇不同，這次這個課題下的課件本身就有兩篇——因此這次粗讀的是兩篇中的第一篇完整部分；下週則會讀第二篇。

由於沒有課件文稿，因此PPT部分以翻譯為主，打星號的部分是我的個人理解或補充，主要是對課件中一些值得展開介紹的部分補充分析或外部信息。

一、引入與概述

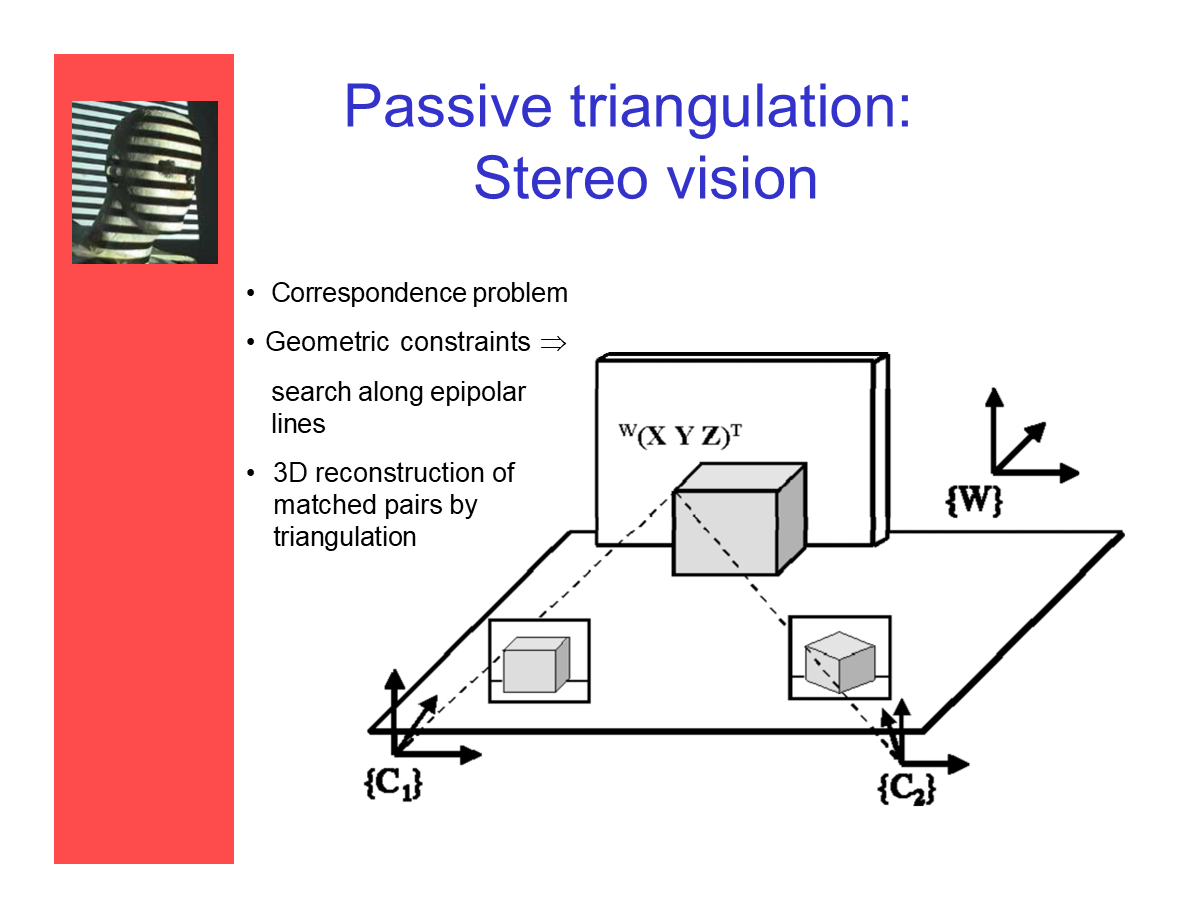
被動三角測量：立體視覺

對應點問題
幾何約束——沿著極線查找
基於匹配點的三角測量進行三維重建

*基本上概括了立體視覺部分的基本思路，細節的一些矩陣計算在上次讀的部分也介紹了。

實時3D模型獲取（重建）

*這裡面提到了很多演示和鏈接，文末會附整篇課件的原文。雖然當時的一些設備還相對比較簡單，但也反映出了這項方案的最小可運行規模。

結構光

——基於攝影測量的主要問題：

為從多個視圖中還原場景物體的形體，我們需要找到圖中的對應點。
這一匹配（對應）問題是很難的。
沒有較好定義過的圖像點集，就無法在圖像域中還原3D物體的幾何結構。

——結構光方案：

理念：通過同構（相似）的點集合，找到一種方式來簡化匹配和確保獲知密度覆蓋信息。
基本策略：使用照明設備來人為創造對應點。

或許是實踐中最為穩固（魯棒 robust）的方案。
被廣泛使用（工業測量、娛樂產業...）。
也被稱為“動態立體視覺”或“白光掃描”。

基礎原則

——光投射：

使用一個投射器來創造無歧義的對應關係。
通過這些對應關係，應用常規的立體（視覺）。
如果我們僅投射一個點，則匹配結果是唯一的。
...但這樣要覆蓋一個物體則需要太多圖片。

特殊情況：光點立體視覺

圖中：基於基本的光點立體解析的常規設備設置方案。

校準相機：通過左右側攝像機的探測以完全確定點的3D位置。光點掃描跨越整個場景。

變體應用

——紋樣投射：

投射一個紋樣而不僅是一個點。
只需要一張圖，記錄一次拍攝。
...但是匹配結果可能不再是唯一的（儘管還是足夠簡單）。
後續（第二篇）會展開介紹。

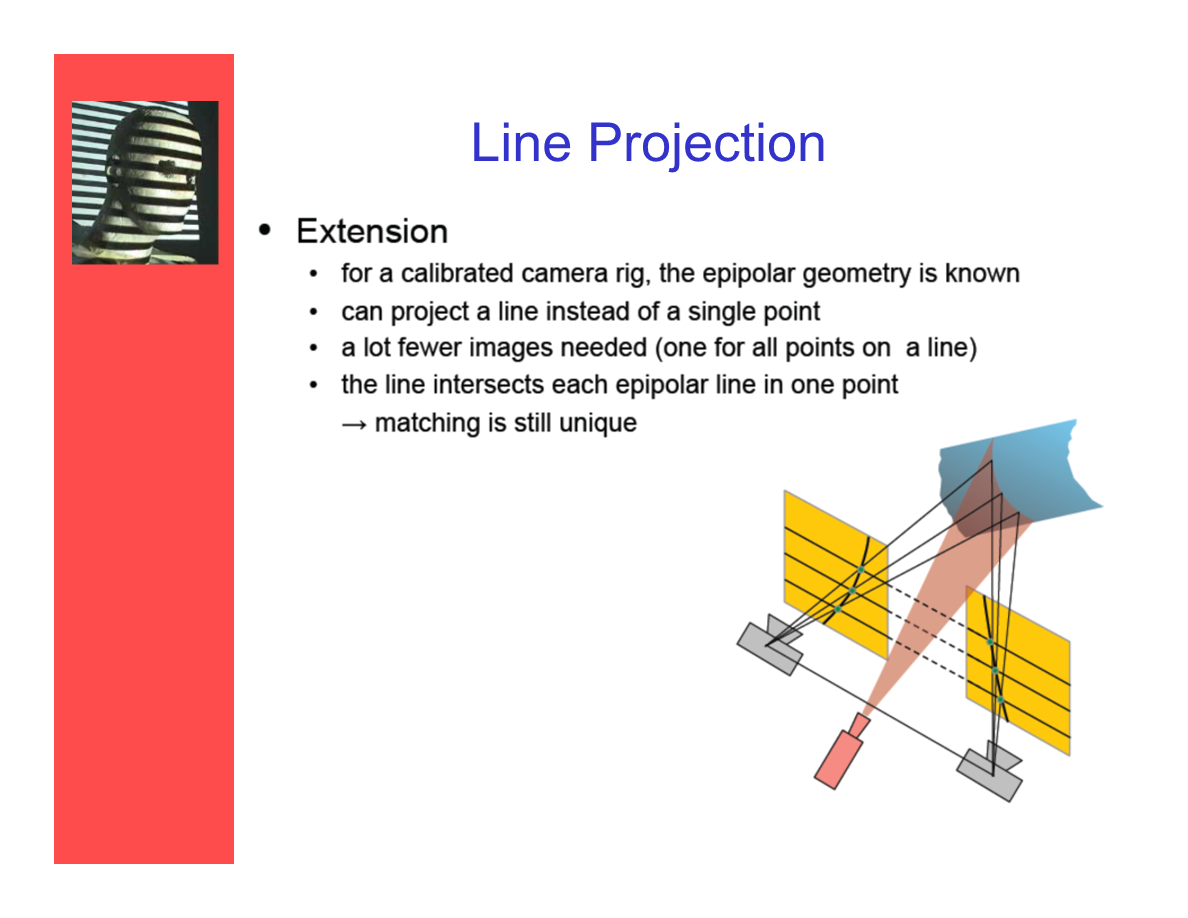
線投射

——擴展：

對於一個校準攝像機裝置，它的對極幾何（固有屬性）是已知的。
可以投射一條線而不是一個點。
需要相對更少的圖片（每條線上的所有點一張）。
掃描線與極線在一個點相交——匹配結果仍然是唯一的。

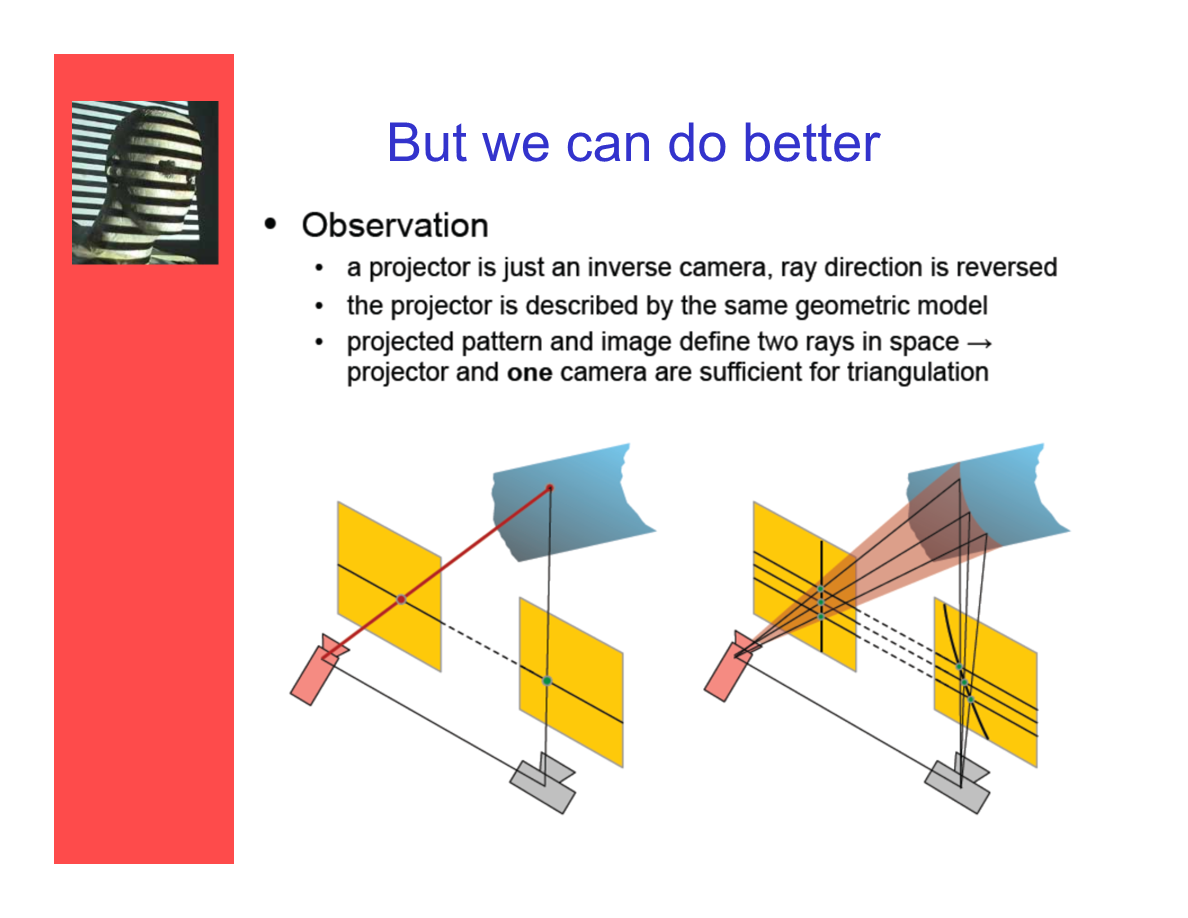
但我們能更進一步

——觀察：

一個投射器可以理解成一個“逆攝像機”，射線的方向是逆向的。
投射器被以（和攝像機）相同的幾何模型來描述。
投影紋樣和圖像定義了空間中的兩條射線——投影器和一臺攝像機就足夠進行三角測量了。

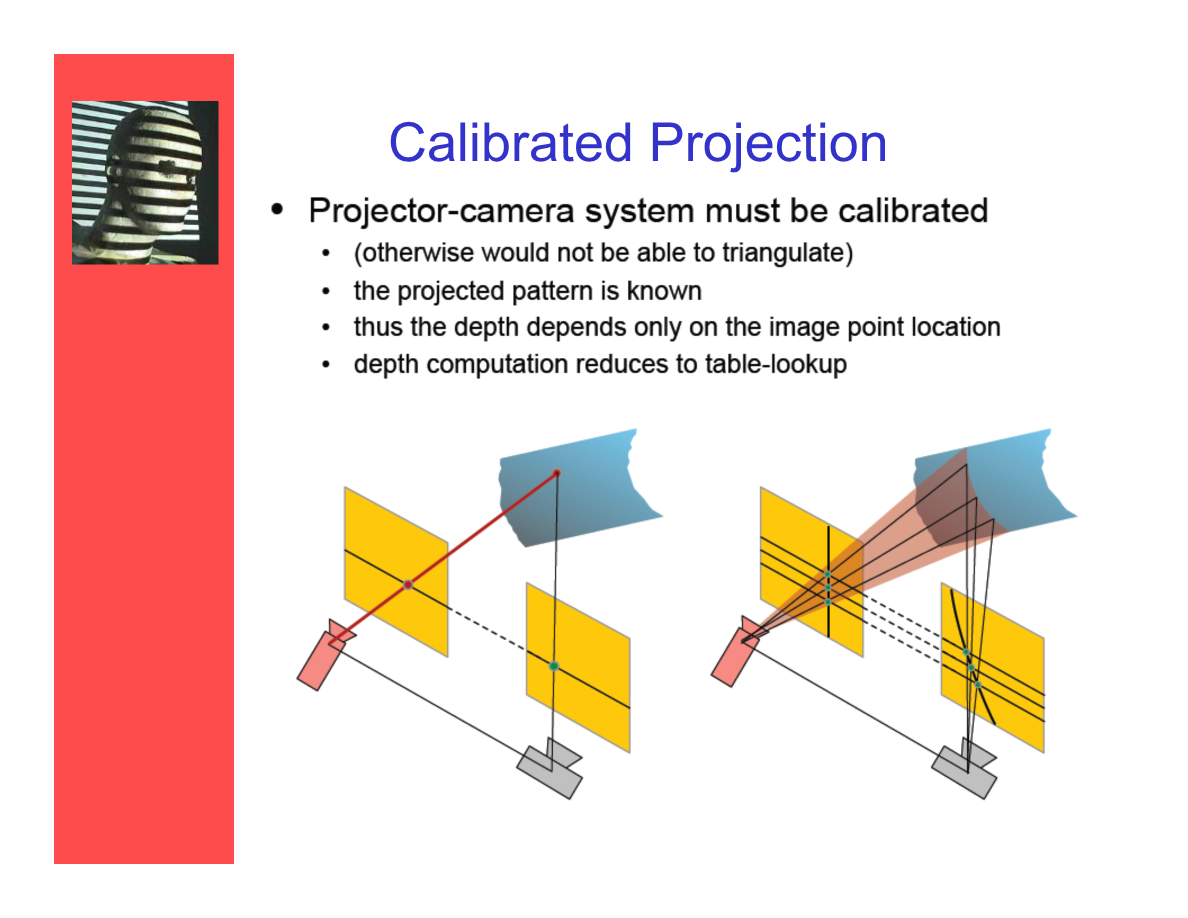
校正投射

——投射攝像機系統必須經過校正：

（否則無法進行三角測量）。
投射紋樣是已知的。
因而深度計算僅依賴於圖像上點的位置。
深度計算能簡化成查表的過程。

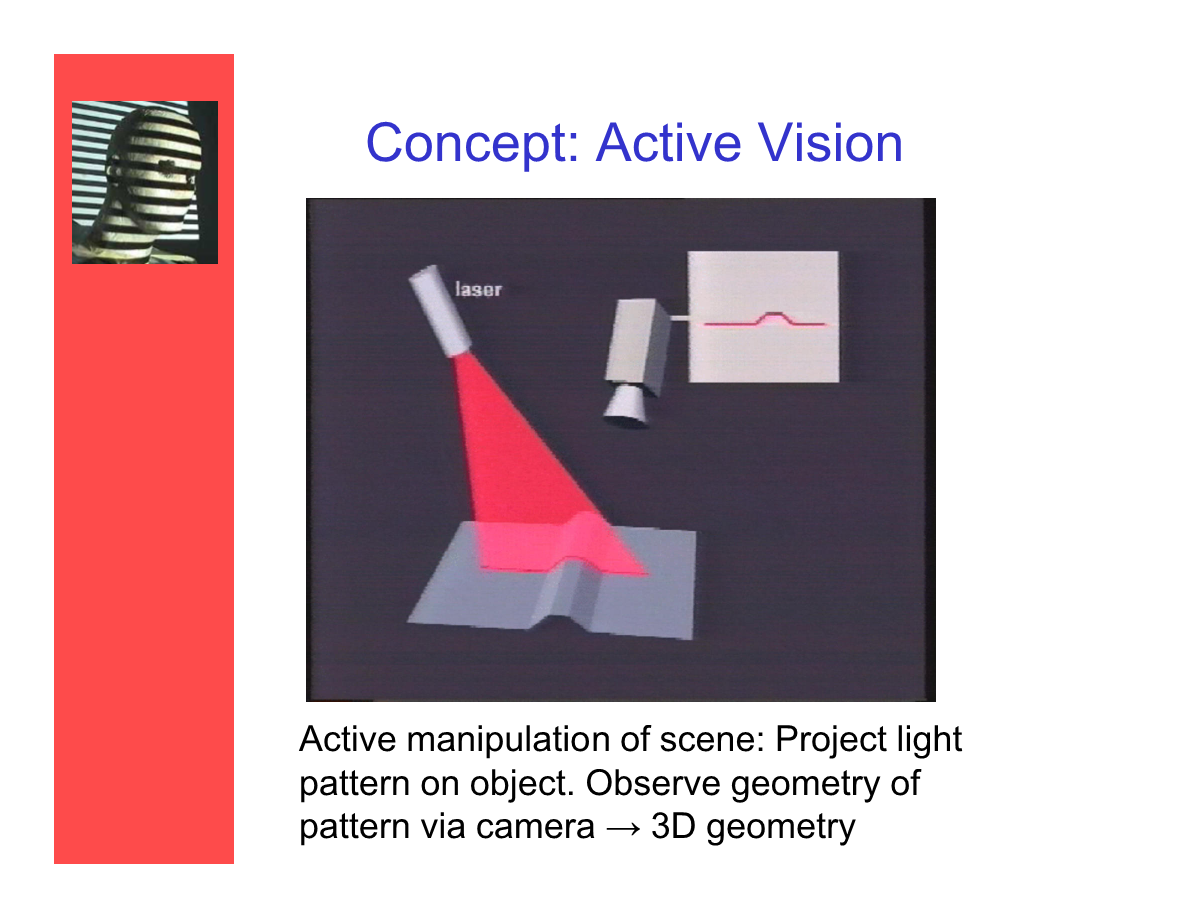
概念：主動立體視覺

主動對場景做操作：對物體投射光紋樣——通過攝像機觀測紋樣——還原3D幾何。

主動3D掃描的一些案例

典型的應用

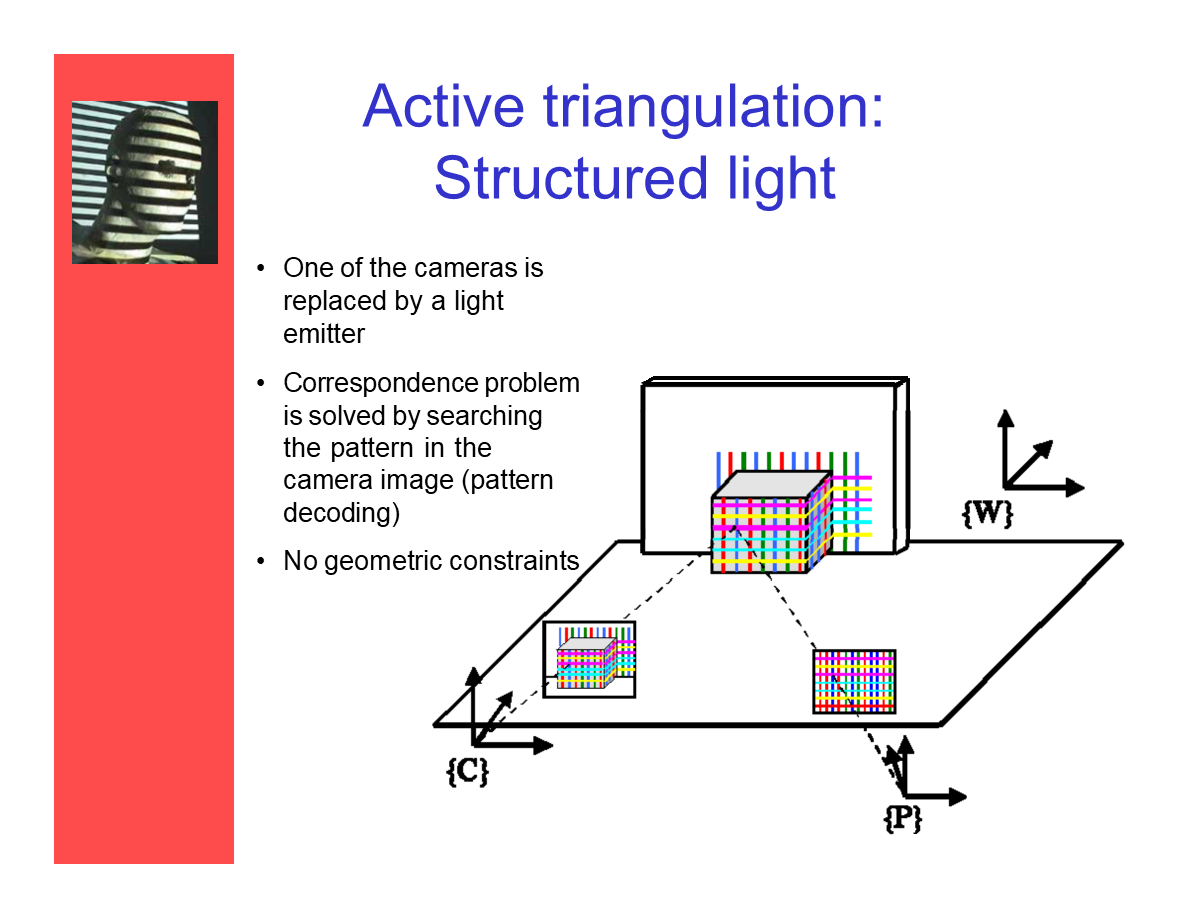
主動三角測量：結構光

其中一個攝像機被光投射器代替。
對應點問題被轉化為在攝像機對應圖像中進行紋樣查找的問題（紋樣解碼）。
沒有幾何約束。

概述

*從概述來看，這部分內容我按邏輯接近程度拆成了4節。

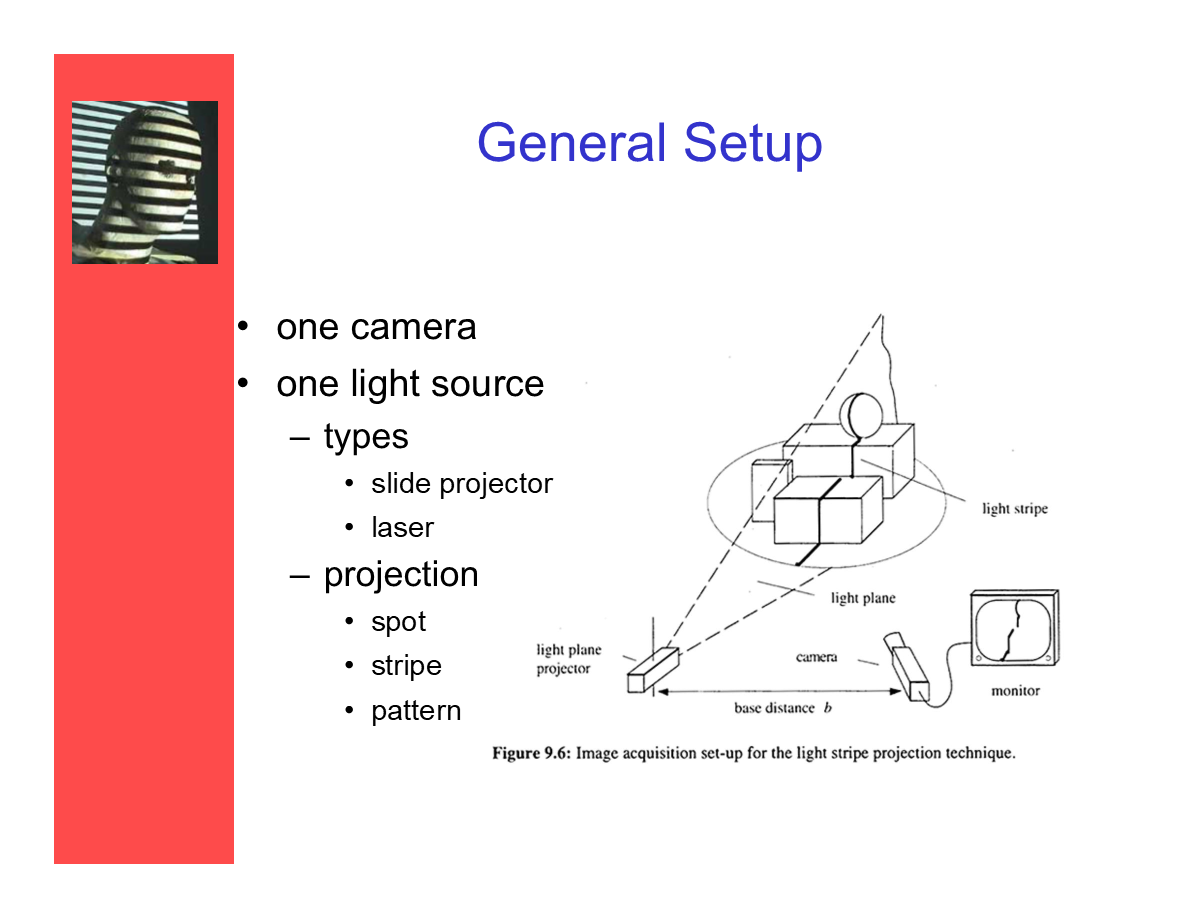
基礎設置

一個攝像機。

一個光源：

——類型：滑動投射器；激光。
——投射：點；帶狀；紋樣。

二、光點投影

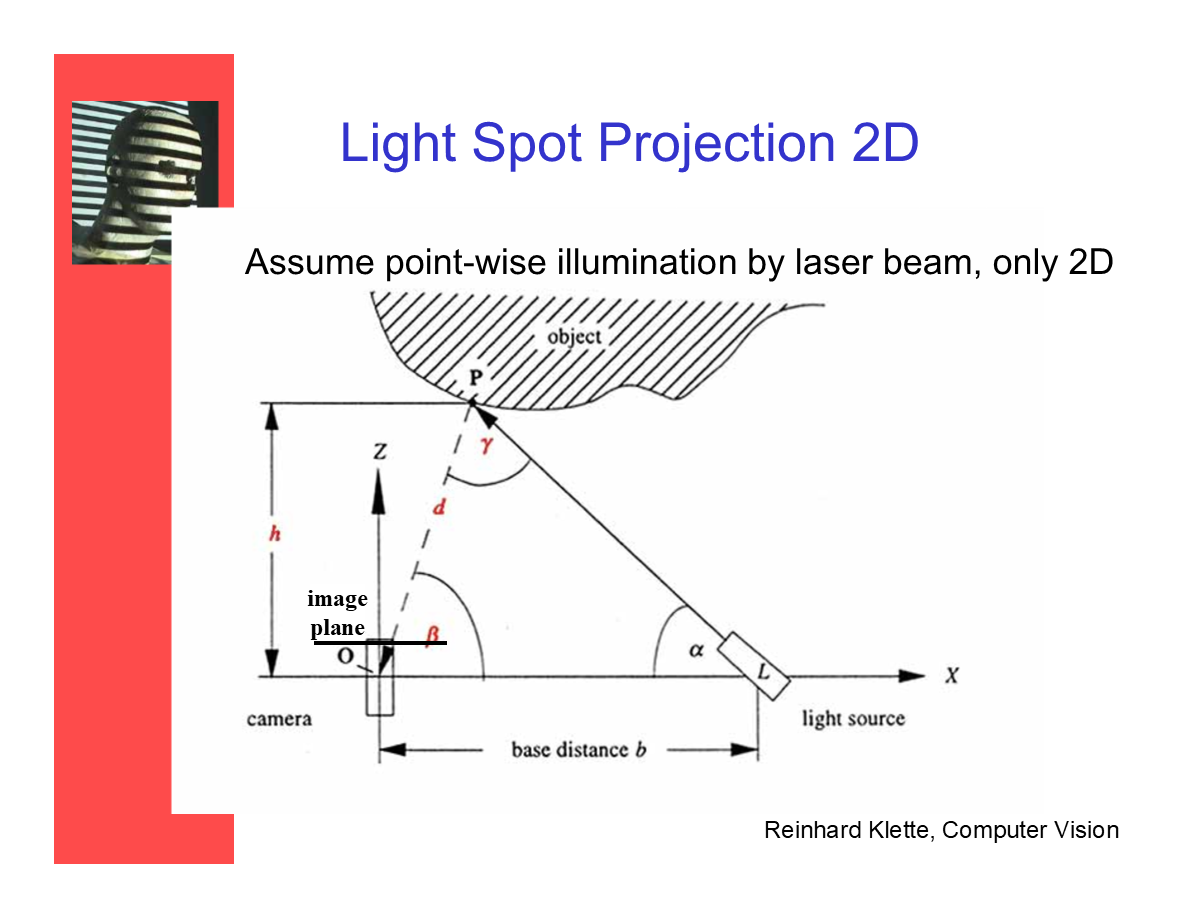
2D光點投射

假設激光束在2D平面上進行逐點式照明。（即設備只考慮水平距離及旋轉，接收設備視為一個線段而不是平面）

O、L和P點定義了一個三角形，並且我們通過三角測量確認了P點的（空間）位置——使用瞭如圖中公式的基礎三角函數sine法則。

通過三角測量可得出的座標：

β可以通過（攝像機）投影幾何得出。
d值的計算（見圖中公式）。
P的座標用X0，Z0表示——分別可以用d與β的三角函數計算出。

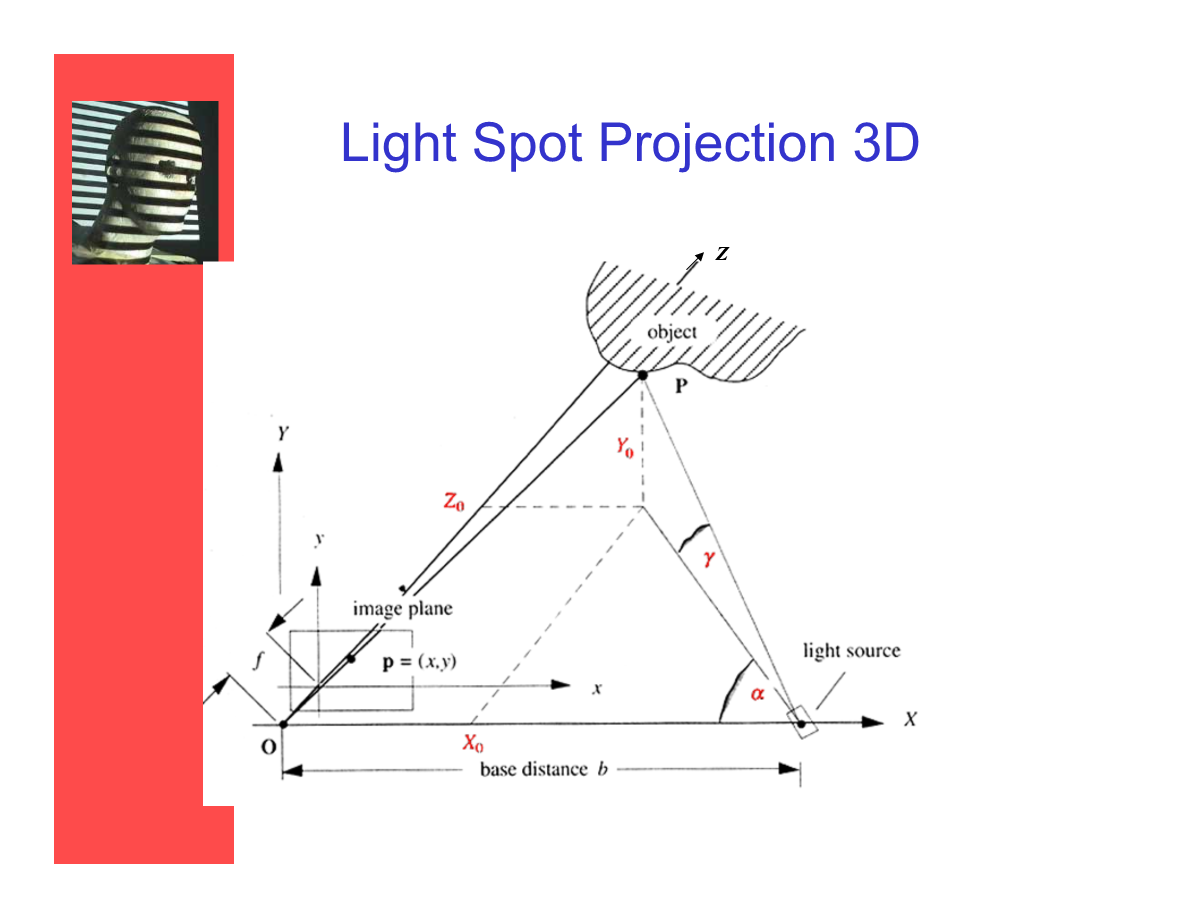
3D光點投射

*3維的情況引入了y軸，接收投影的變成了平面——投影點p位於該平面上。

*發射角度上，除了水平角α，還引入了垂直角γ。

*這裡在設備設置後，α和b都是已知給定的。

*根據中心點投射的射線定理（ray theorem）——P點的座標XZY和xfy成正比，其中xy是投影平面上的點p的座標，f是中心點O到投影平面的距離（寫作f其實就是焦距）。

*對於XZ平面上的角α來說，tanα = Z / (b - X)。

*結合前面兩個結論可以分別推導出XYZ和tanα的關係（如圖）。

最終可以根據α、b 、f、x、y分別計算出X0、Y0、Z0。

一個觀察，這部分計算中並沒有用到垂直角度γ。

*即根據設備基礎的位置角度信息，及投影座標x、y即可計算點P的座標。

三、光帶投影

光帶掃描——單條

光學三角測量：

投射單個激光條
用它掃描物體的表面
這是結構光掃描的一個非常準確的版本
利於生成高精度的3D結果，但需要大量的時間以拍攝很多圖片

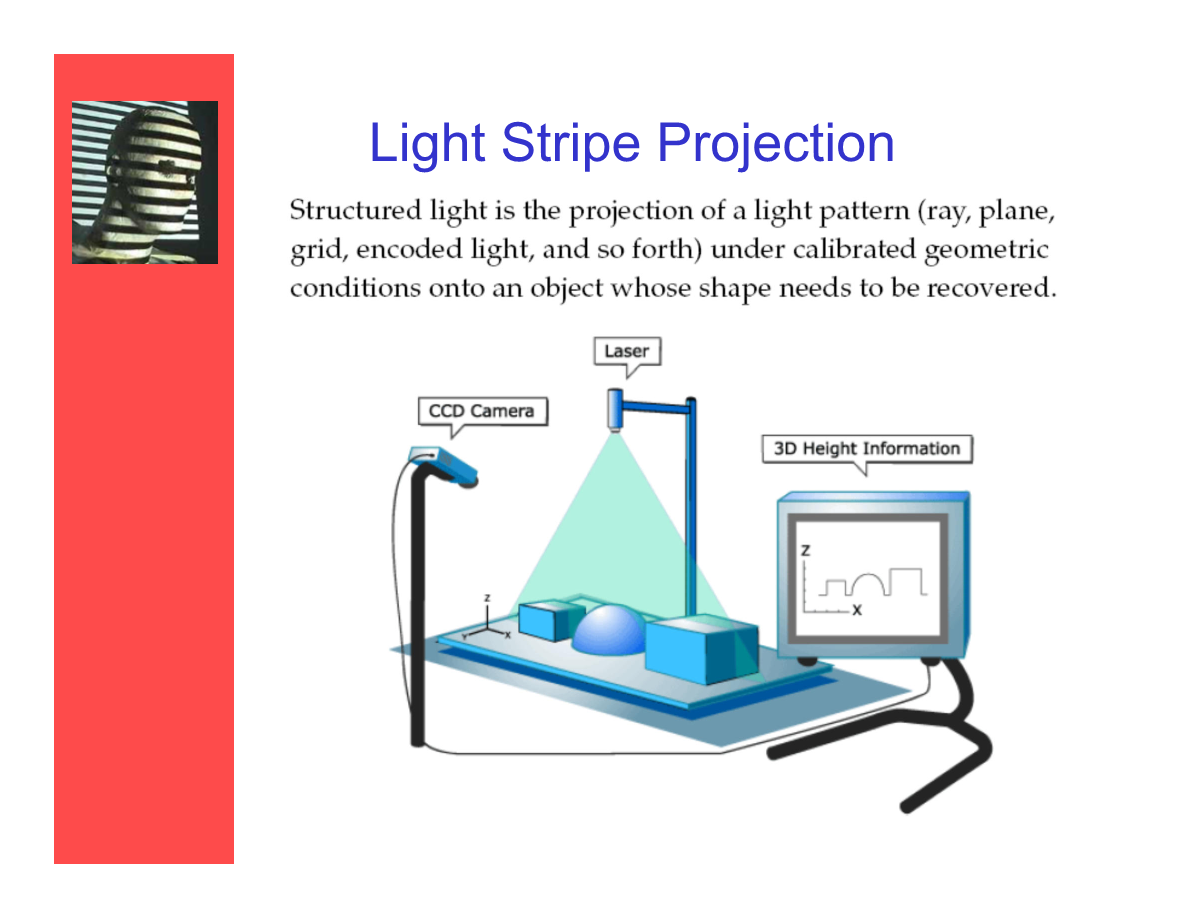
光帶投射

結構光方案是——在校準過的幾何條件下向目標物體投以一個光紋樣（射線、平面、柵格、編碼的光源、以及其它），並進行三維重建。

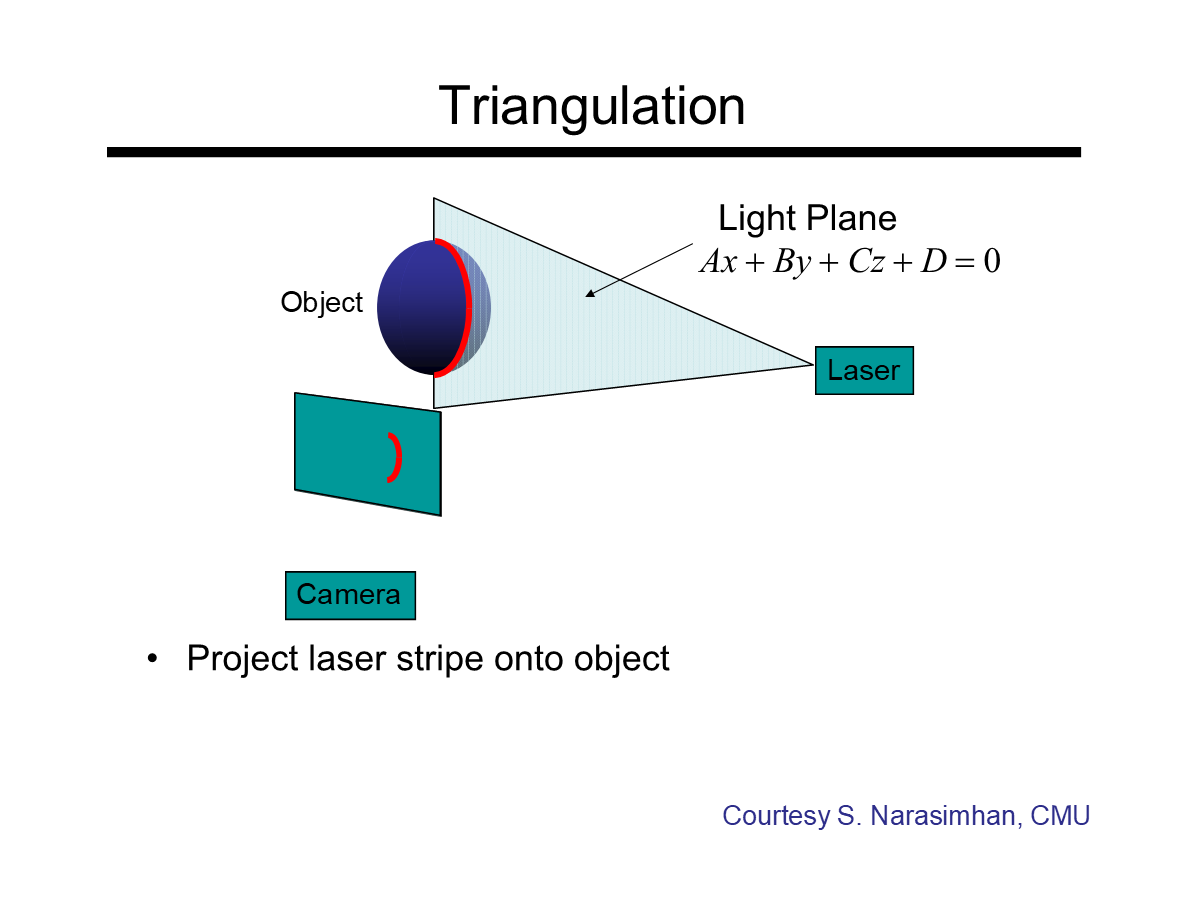
（結構光的）三角測量

*這個案例中激光發射出的是一個“光平面”，它會與物體表面相交投下光帶。平面的表達式如圖——基於攝像機光學中心為座標原點。

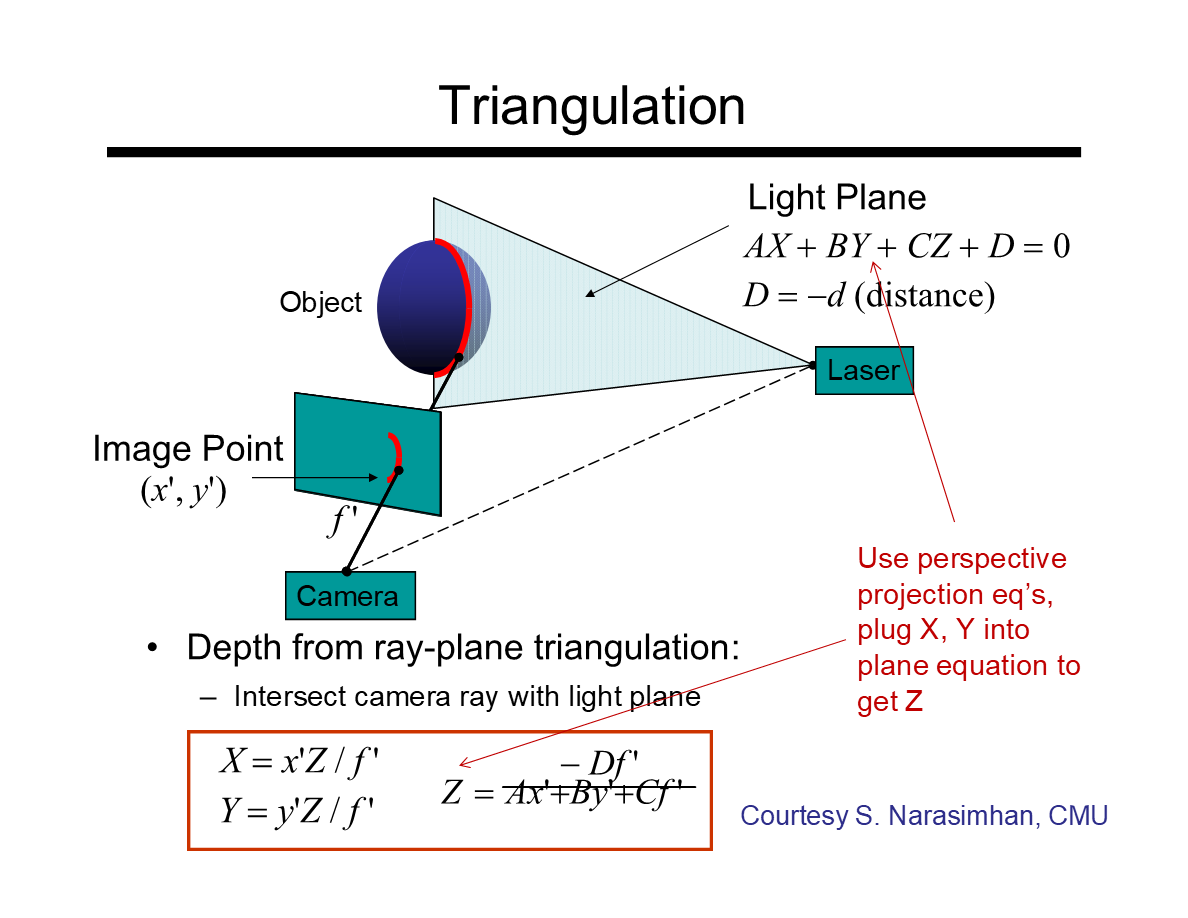
*圖中信息較多，這裡實際是要在已知一個投影點（x'，y'）及當前投影校準幾何相關信息的前提下，計算三維空間的深度——也就是Z值。

*對於一個點的情況，參照前一節提到的單點三維投射：X/x' = Z/f' = Y/y' 的結論仍是成立的，因此可以得到X、Y值基於Z的表達式（如圖）。

*D = -d。其中d是光平面到攝像機光學原點的距離。因為平面方程中ABC的幾何意義是平面的法向量，D可以理解成將平面移到座標原點的距離。

*將已知的x'、y'、f'、D、A、B帶入公式即可得出Z值（如圖）。在這種座標設置下，Z值就是物體上的點相對於攝像機的深度值。

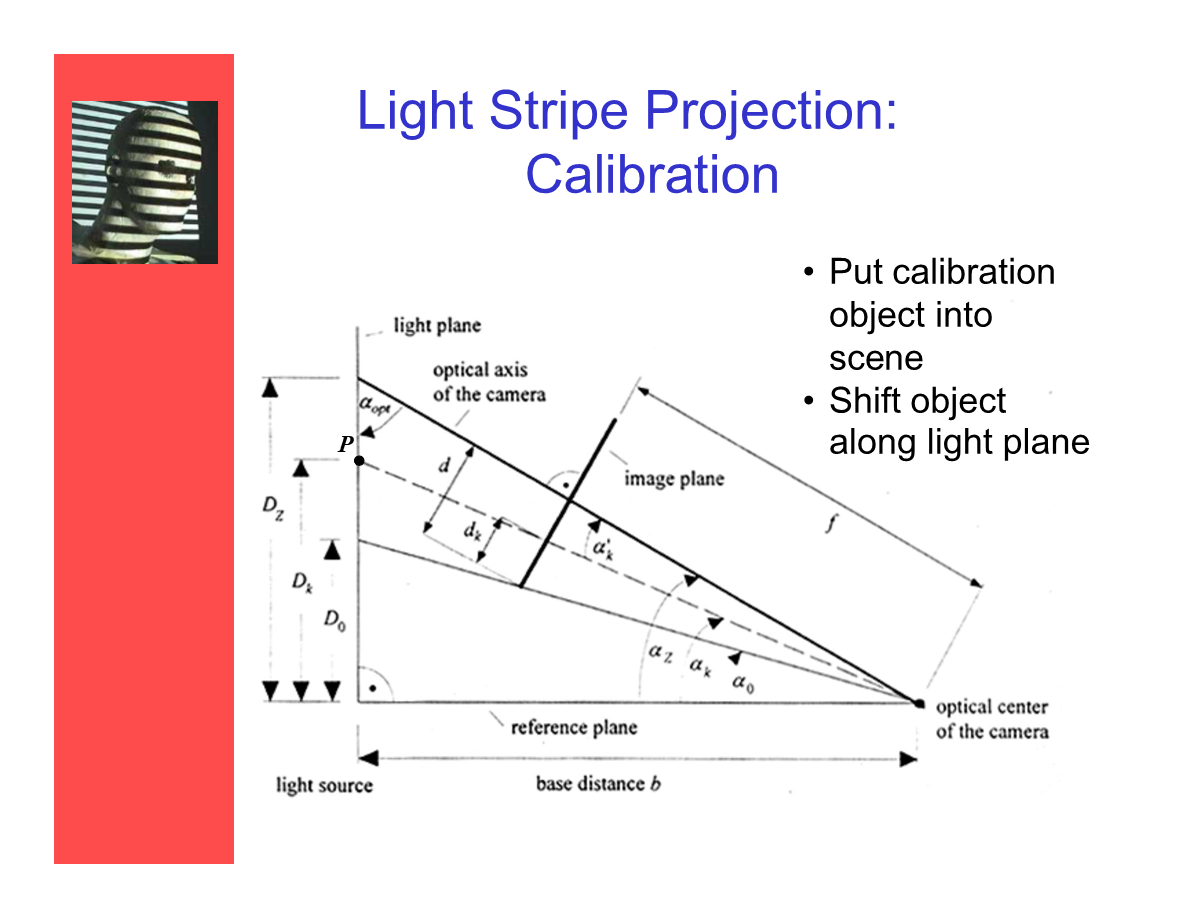
光條投射——校正

將校正物體放入場景，並沿著光平面平移。

*圖中從頂視圖展示了各個幾何關鍵點的位置關係。通過校準計算可以得出光平面相對於光學原點的平面參數。

距離校正

要校準一個固定光平面的系統的距離，一個簡單的方法是假設目標物體在一個“轉盤”上，其旋轉中心是光平面的原點。

校準平面在兩點——max和min之間移動，與光平面平行。在最大值處，（攝像機的）圖像中最右側的列會被照亮，在最小值處則是照亮最左側的值。對於每一列y我們測量其在光學平面的Z值，這就是滿足y列被照亮的校準平面的座標值。

*這部分直接翻譯理解上可能有點抽象，其實旋轉和距離是兩個關切點。結合後面的例圖應該更好理解一些。

更直接的方法：單條光帶與旋轉物體

轉盤上的物體：

對每一個旋轉位置和光窄口（slit）創建對應的輪廓P（X,Y,Z）。
以離散的間隔旋轉物體，並重復這一過程。
以柱面方式集成輪廓信息，以重建3D物體——以3D網格的方式。

*注意這裡的多條紋是集成後的結果。

示例：激光掃描器

優點：非常精確，誤差在0.01毫米以內。

缺點：需要10秒以上時間完成一次掃描。

便攜式3D激光掃描器示例

四、3D拍攝與其它輕量級的方案

基於陰影的3D信息獲取

*這裡列出了這一節討論的內容的論文出處，有興趣的可以按需搜索。

你桌邊的3D拍攝工具

使用常規工具以“便宜”的方案進行3D拍攝。
需要：PC、攝像機、棍子、檯燈、棋盤板。
使用“弱結構光”方案。

設備設置示意圖

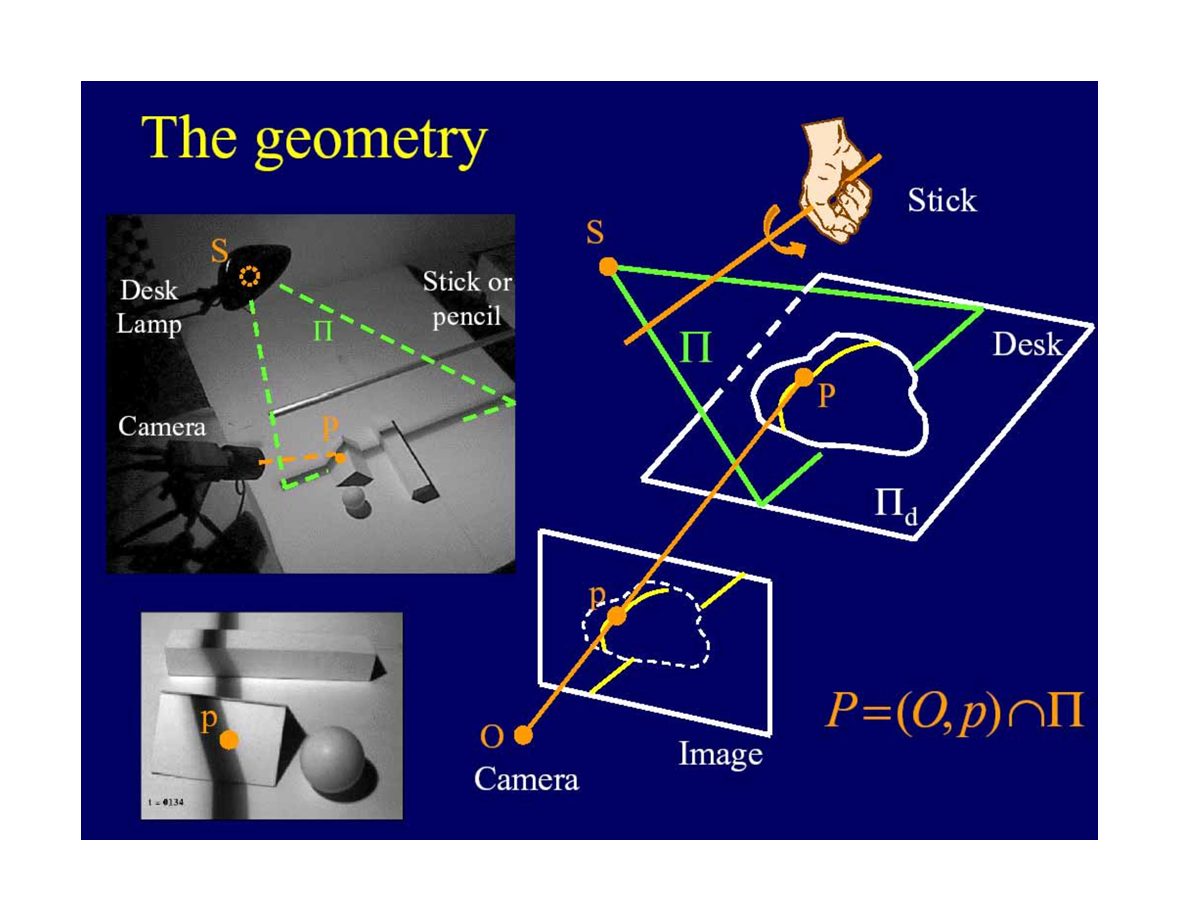
*可以看到，這裡的棍子的陰影起到了之前光帶的作用。

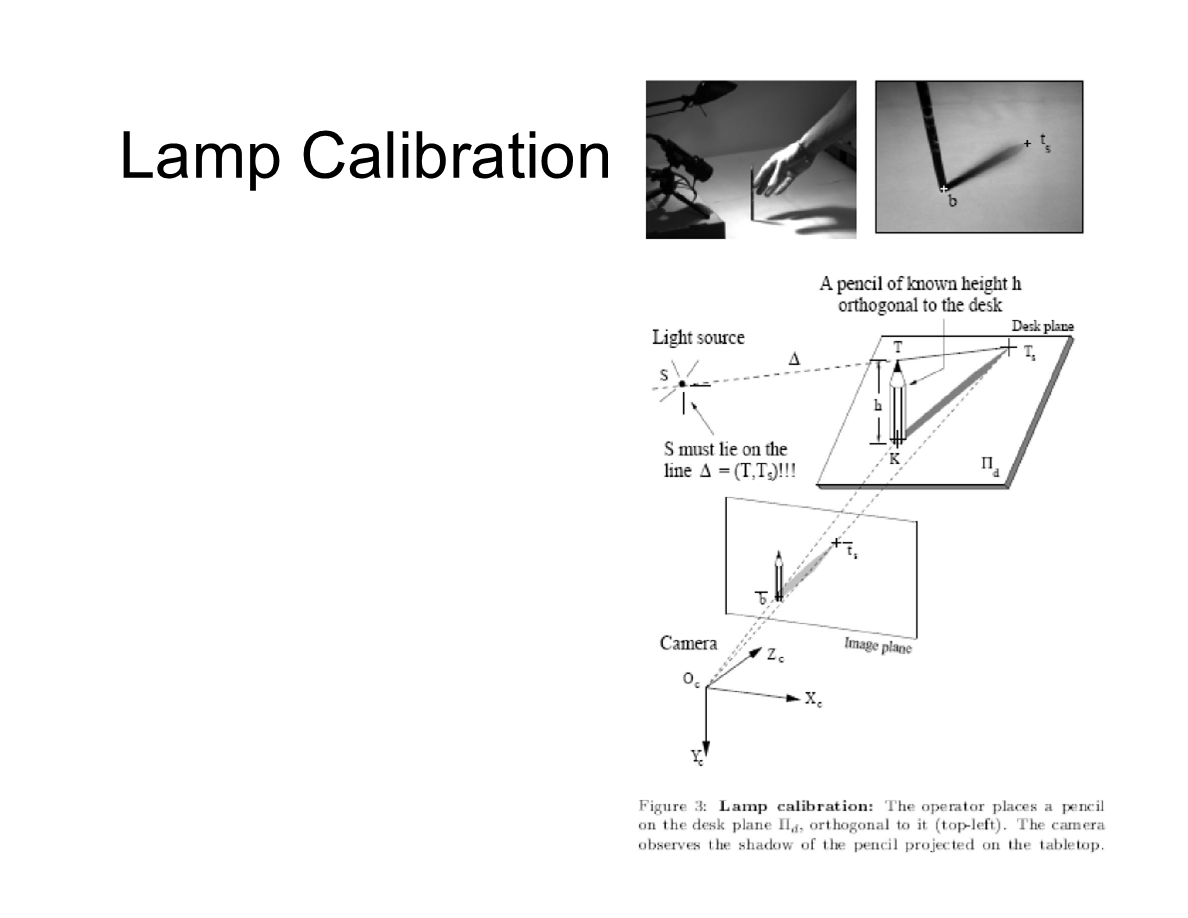
檯燈校準

檯燈校準：操作者在桌面放置了一根鉛筆，與其垂直。在攝像機中觀測鉛筆在桌面投下的陰影。光源中心S需要在T和Ts的延長線上。

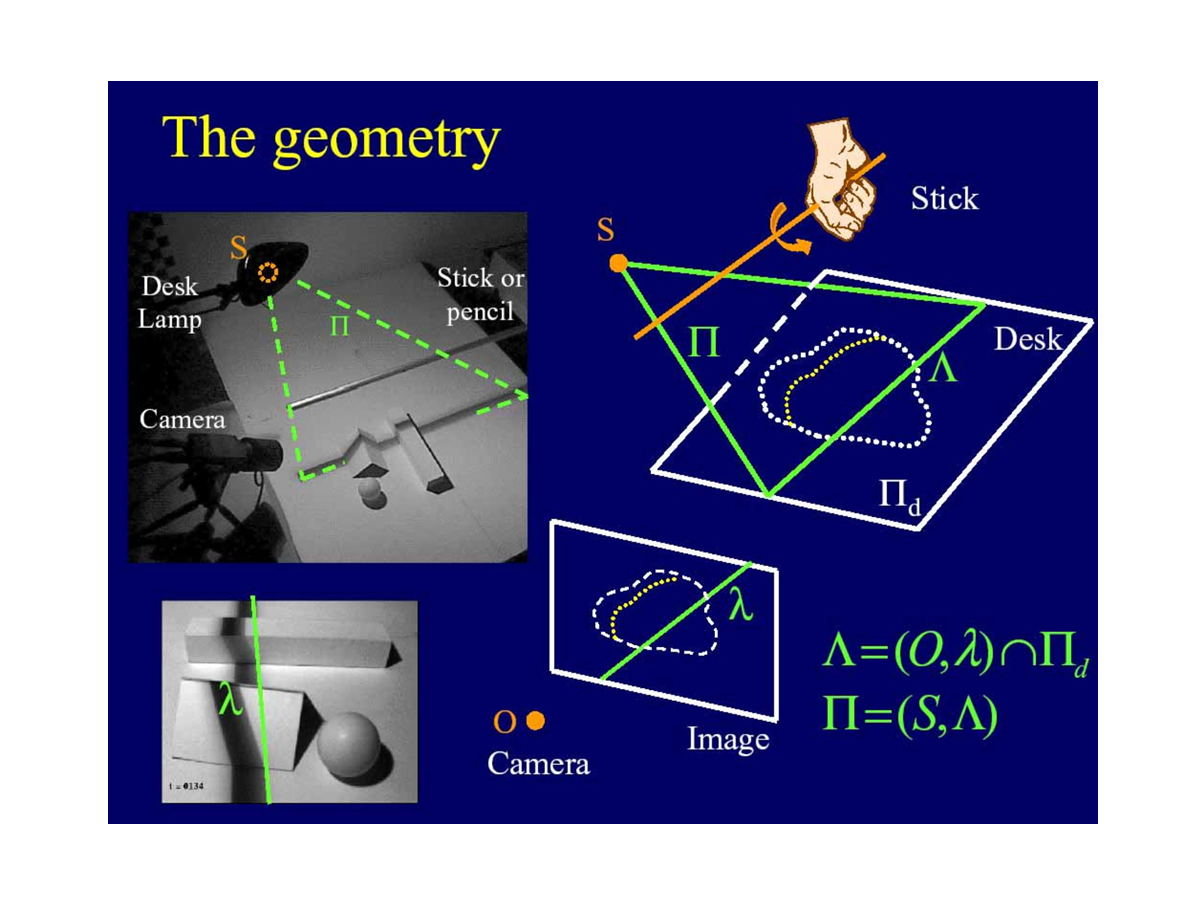
當棍子與桌面平行時

* ∩ 是相交的符號， Λ 是平面（O， λ）與 Π d的相交直線。

*Π是由S和Λ確定的平面。在確定了“人造光平面”後，問題就轉化為了前一節解決的問題。

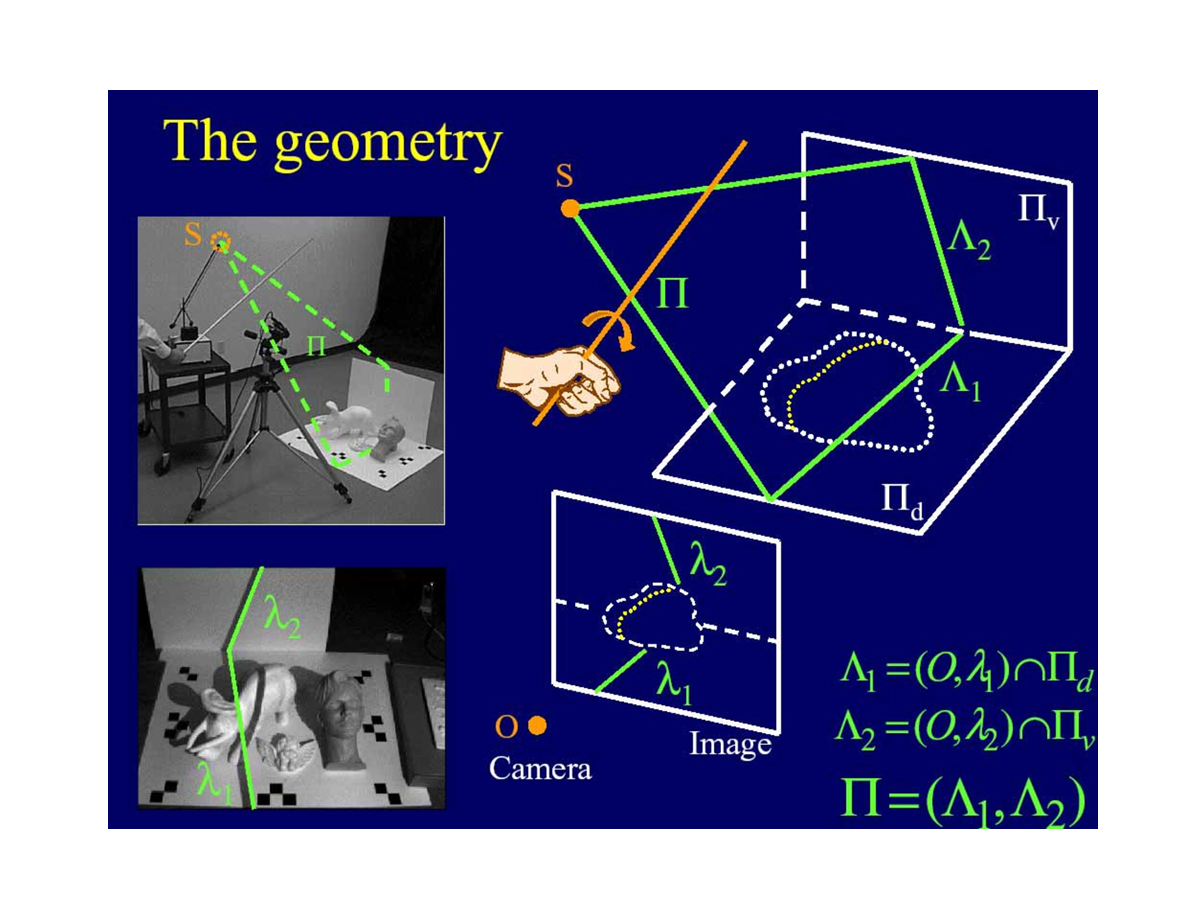
當棍子與桌面有角度時

*這裡額外引入了一個平面和一根線，最終用兩條相交線確認了平面Π 。推導方式和前一頁原理相同。

天使實驗

*從圖中可以看出，這種方法誤差是0.1%，但也有一些位置信息不能很好的確定——和陰影寬度有關。

基於日光的掃描

*圖中雖然是黑白的，但是主要思路是用細棍在車身投影。誤差是 0.5% 。

大家都能使用的低成本3D掃描器

*從圖中可以看出掃描小物體需要的設備尺寸及掃描情況。

*圖中是2009年的一篇SIG文章，其中介紹了包括結構光在內的一些常見的3D掃描技術。

結語

通過粗讀這篇課件，我們瞭解了結構光方案作為一項“主動”方案在確定性及便捷性上的優點。在本篇的最後停在了光帶（或人造陰影條）進行掃描測量的部分，涉及的計算沒有超出立體幾何的範圍。

這個系列兩篇文章的下一篇會介紹以“編碼紋樣”進行結構光掃描的方案（Pattern encoding/decoding），相對會更難理解一些，但確實也是提升結構光方案效率的必經之路。

下面是資料鏈接：

Structured Lighting Guido Gerig CS 6320, 3D Computer Vision Spring 2015