前言

这周继续读三维重建方面的技术向课件。按照之前的大纲，这次读到前AI时代中，计算机视觉方面的一项技术——

Structured Light（结构光）。这项技术作为立体视觉之后提出的一项技术，其理解跨度相对不算大。

简单来说，这是一项用激光等光源投在物体表面、再用相机等设备进行采样的技术，注重还原物体的三维结构。

介绍结构光的论文其实也很多，但作为个人能全部仔细读完以及图文搭配合适的内容，这次我选择了UTAH于2015年的计算机视觉课件。和之前一篇比较长的PPT拆分成上下两篇不同，这次这个课题下的课件本身就有两篇——因此这次粗读的是两篇中的第一篇完整部分；下周则会读第二篇。

由于没有课件文稿，因此PPT部分以翻译为主，打星号的部分是我的个人理解或补充，主要是对课件中一些值得展开介绍的部分补充分析或外部信息。

一、引入与概述

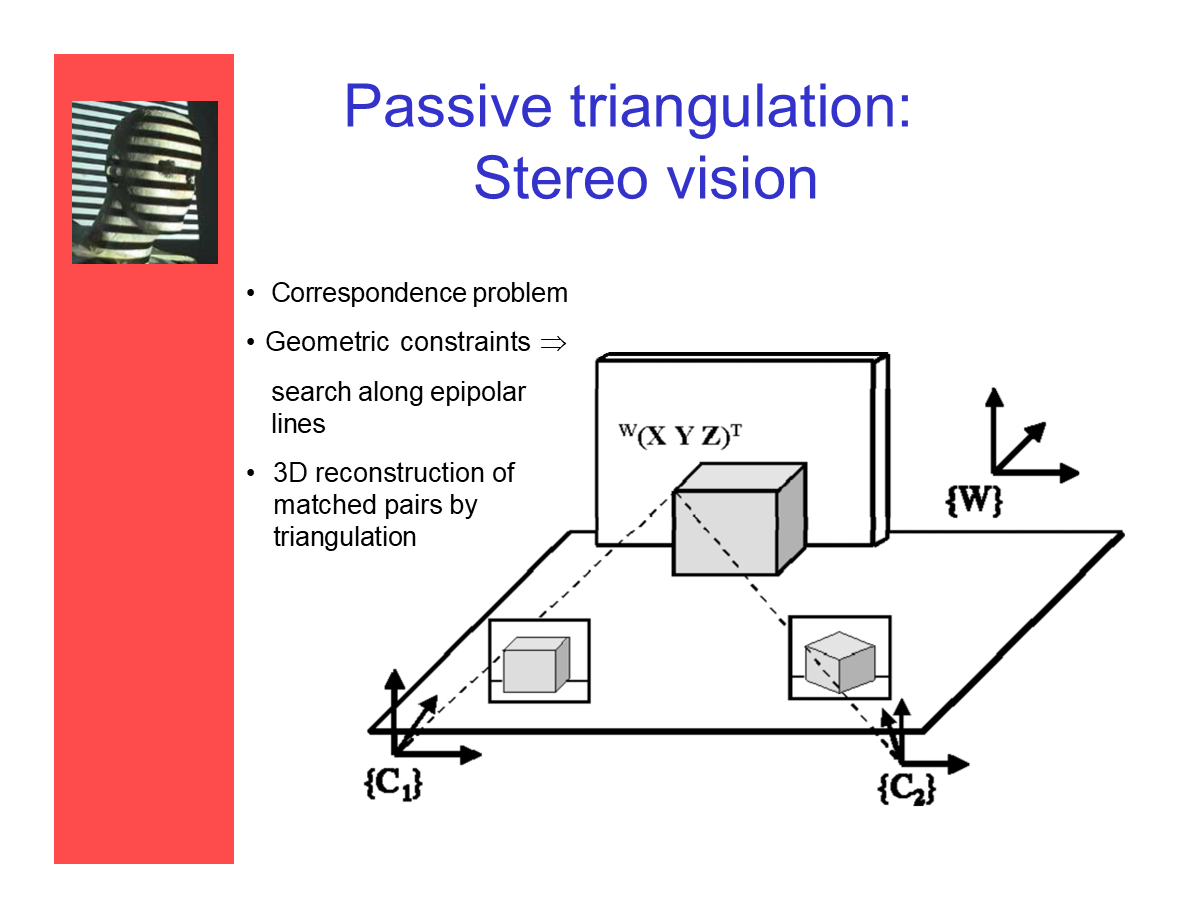
被动三角测量：立体视觉

对应点问题
几何约束——沿着极线查找
基于匹配点的三角测量进行三维重建

*基本上概括了立体视觉部分的基本思路，细节的一些矩阵计算在上次读的部分也介绍了。

实时3D模型获取（重建）

*这里面提到了很多演示和链接，文末会附整篇课件的原文。虽然当时的一些设备还相对比较简单，但也反映出了这项方案的最小可运行规模。

结构光

——基于摄影测量的主要问题：

为从多个视图中还原场景物体的形体，我们需要找到图中的对应点。
这一匹配（对应）问题是很难的。
没有较好定义过的图像点集，就无法在图像域中还原3D物体的几何结构。

——结构光方案：

理念：通过同构（相似）的点集合，找到一种方式来简化匹配和确保获知密度覆盖信息。
基本策略：使用照明设备来人为创造对应点。

或许是实践中最为稳固（鲁棒 robust）的方案。
被广泛使用（工业测量、娱乐产业...）。
也被称为“动态立体视觉”或“白光扫描”。

基础原则

——光投射：

使用一个投射器来创造无歧义的对应关系。
通过这些对应关系，应用常规的立体（视觉）。
如果我们仅投射一个点，则匹配结果是唯一的。
...但这样要覆盖一个物体则需要太多图片。

特殊情况：光点立体视觉

图中：基于基本的光点立体解析的常规设备设置方案。

校准相机：通过左右侧摄像机的探测以完全确定点的3D位置。光点扫描跨越整个场景。

变体应用

——纹样投射：

投射一个纹样而不仅是一个点。
只需要一张图，记录一次拍摄。
...但是匹配结果可能不再是唯一的（尽管还是足够简单）。
后续（第二篇）会展开介绍。

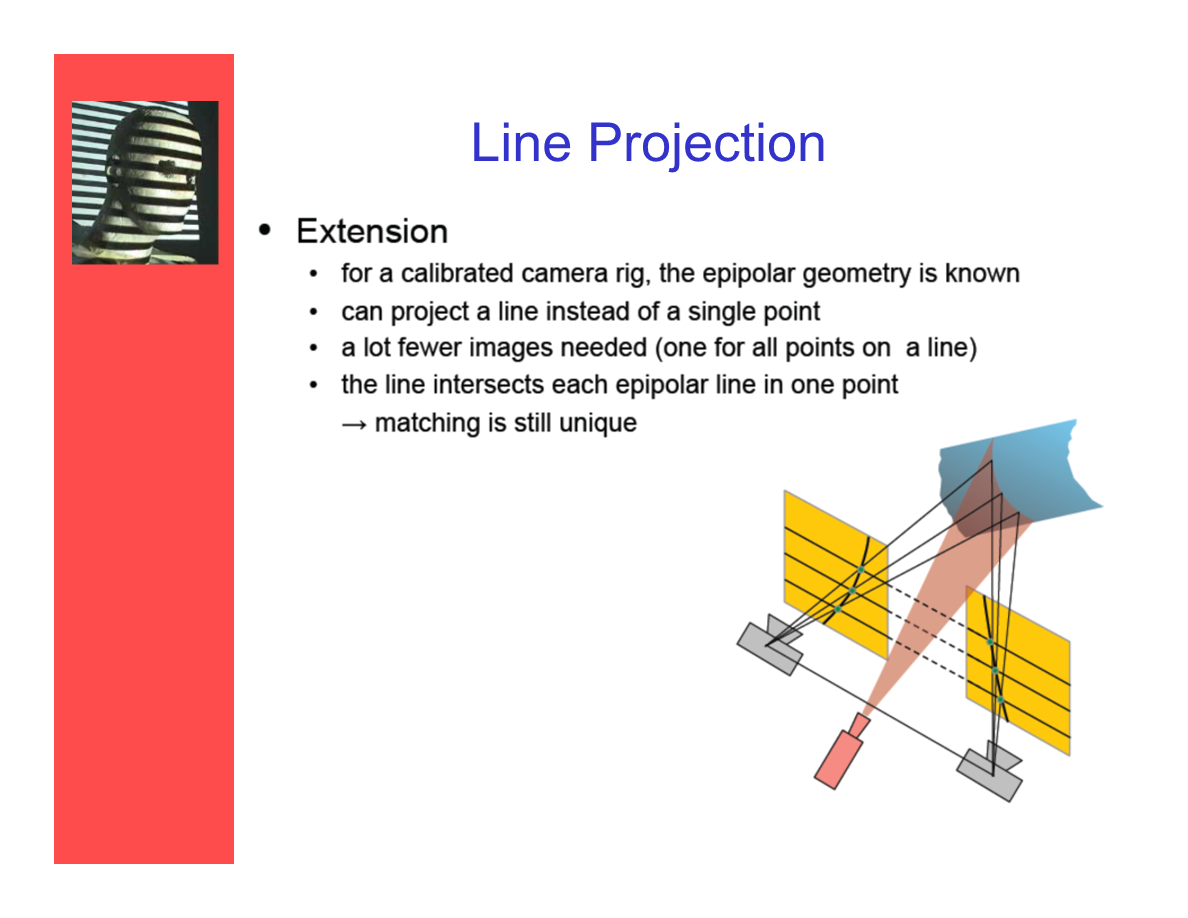
线投射

——扩展：

对于一个校准摄像机装置，它的对极几何（固有属性）是已知的。
可以投射一条线而不是一个点。
需要相对更少的图片（每条线上的所有点一张）。
扫描线与极线在一个点相交——匹配结果仍然是唯一的。

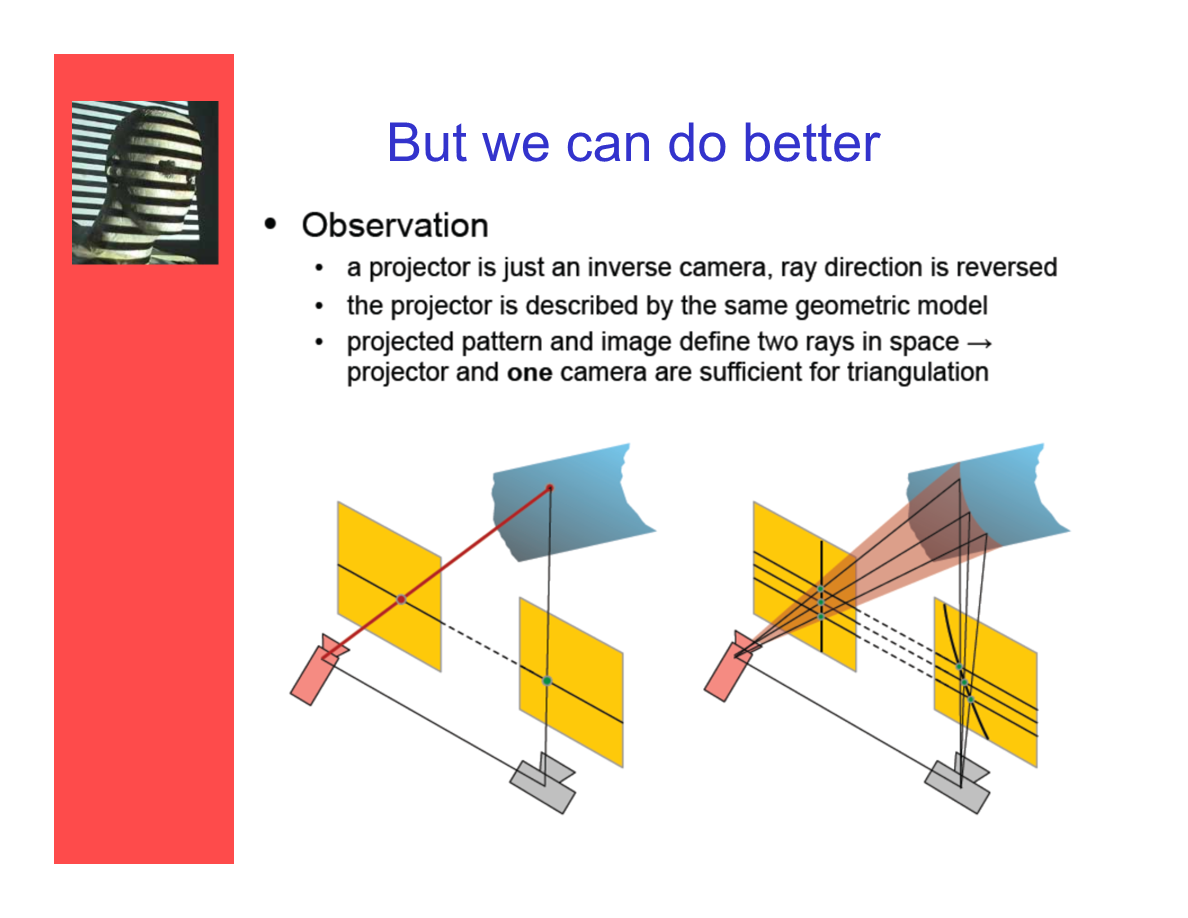
但我们能更进一步

——观察：

一个投射器可以理解成一个“逆摄像机”，射线的方向是逆向的。
投射器被以（和摄像机）相同的几何模型来描述。
投影纹样和图像定义了空间中的两条射线——投影器和一台摄像机就足够进行三角测量了。

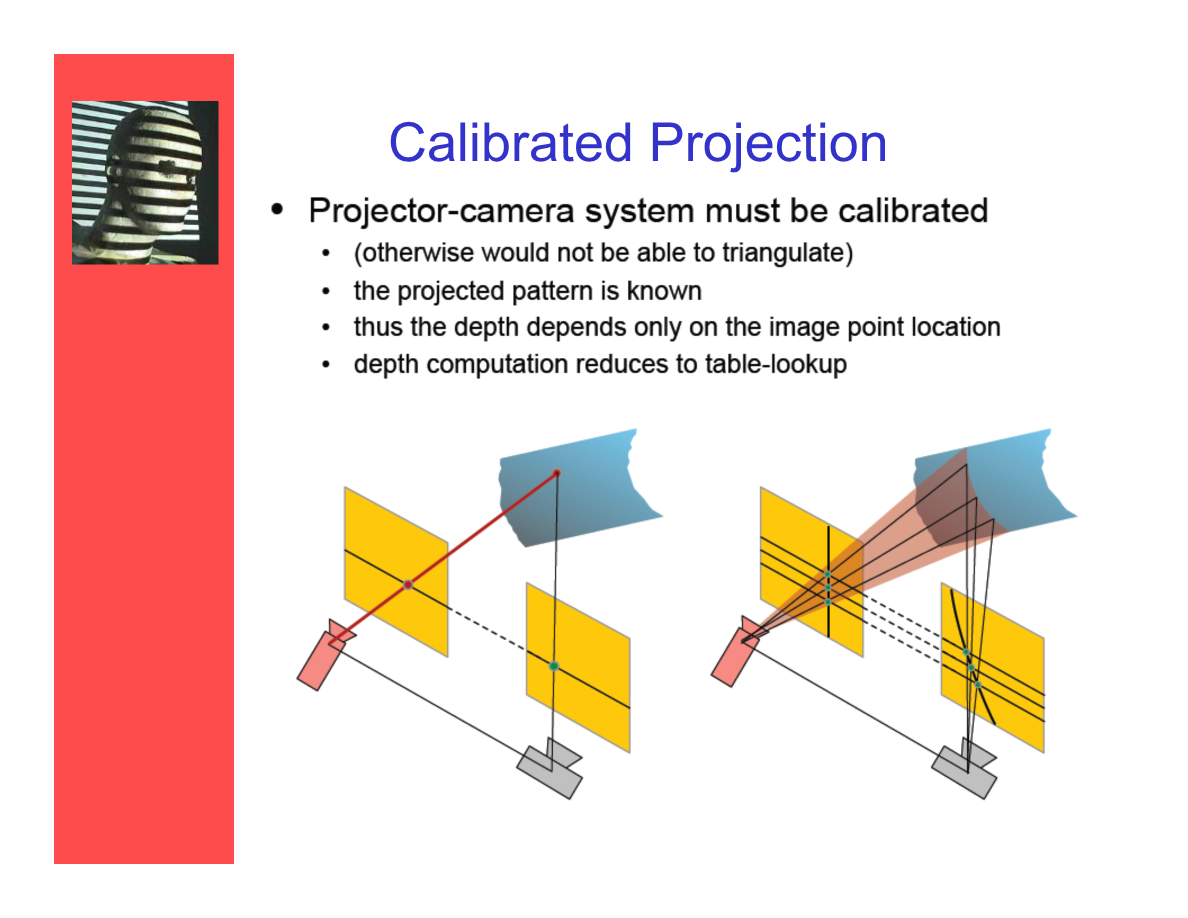
校正投射

——投射摄像机系统必须经过校正：

（否则无法进行三角测量）。
投射纹样是已知的。
因而深度计算仅依赖于图像上点的位置。
深度计算能简化成查表的过程。

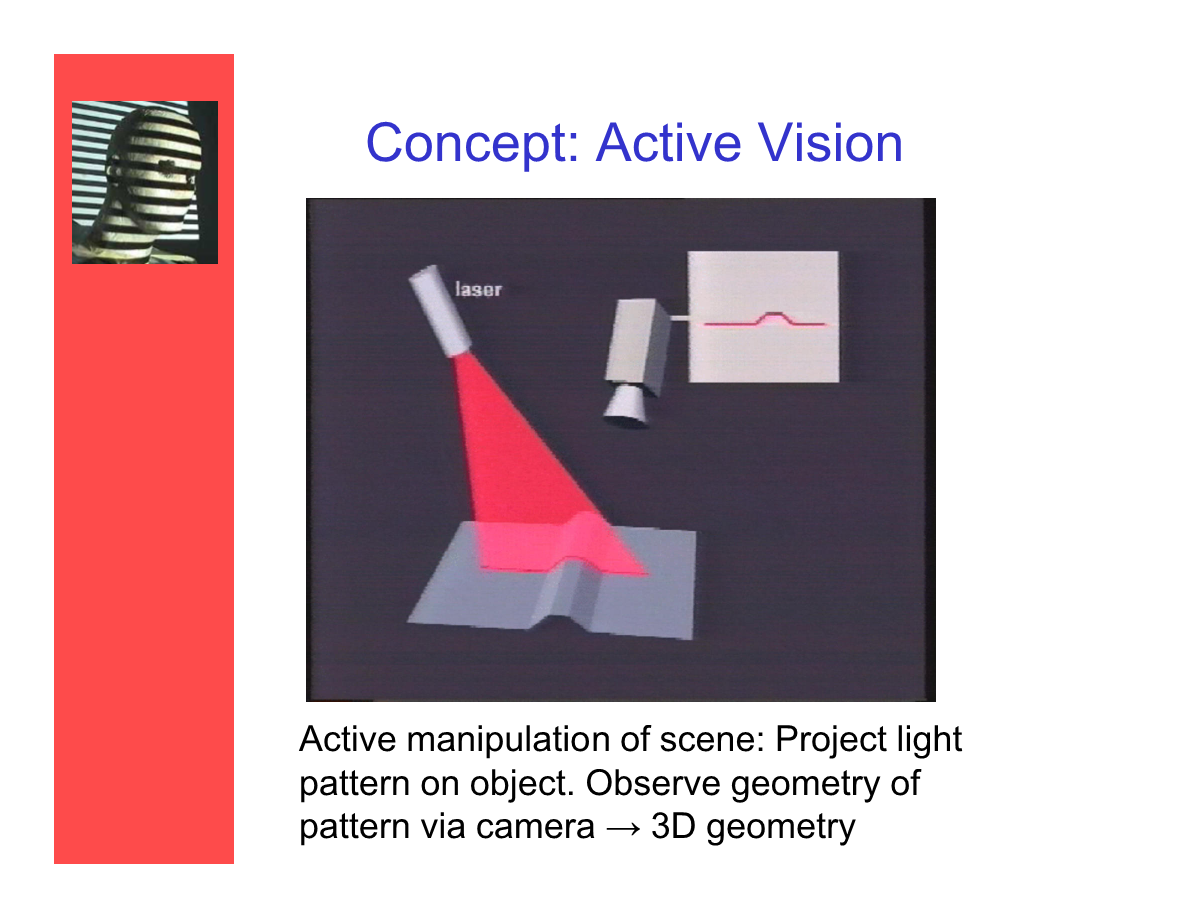
概念：主动立体视觉

主动对场景做操作：对物体投射光纹样——通过摄像机观测纹样——还原3D几何。

主动3D扫描的一些案例

典型的应用

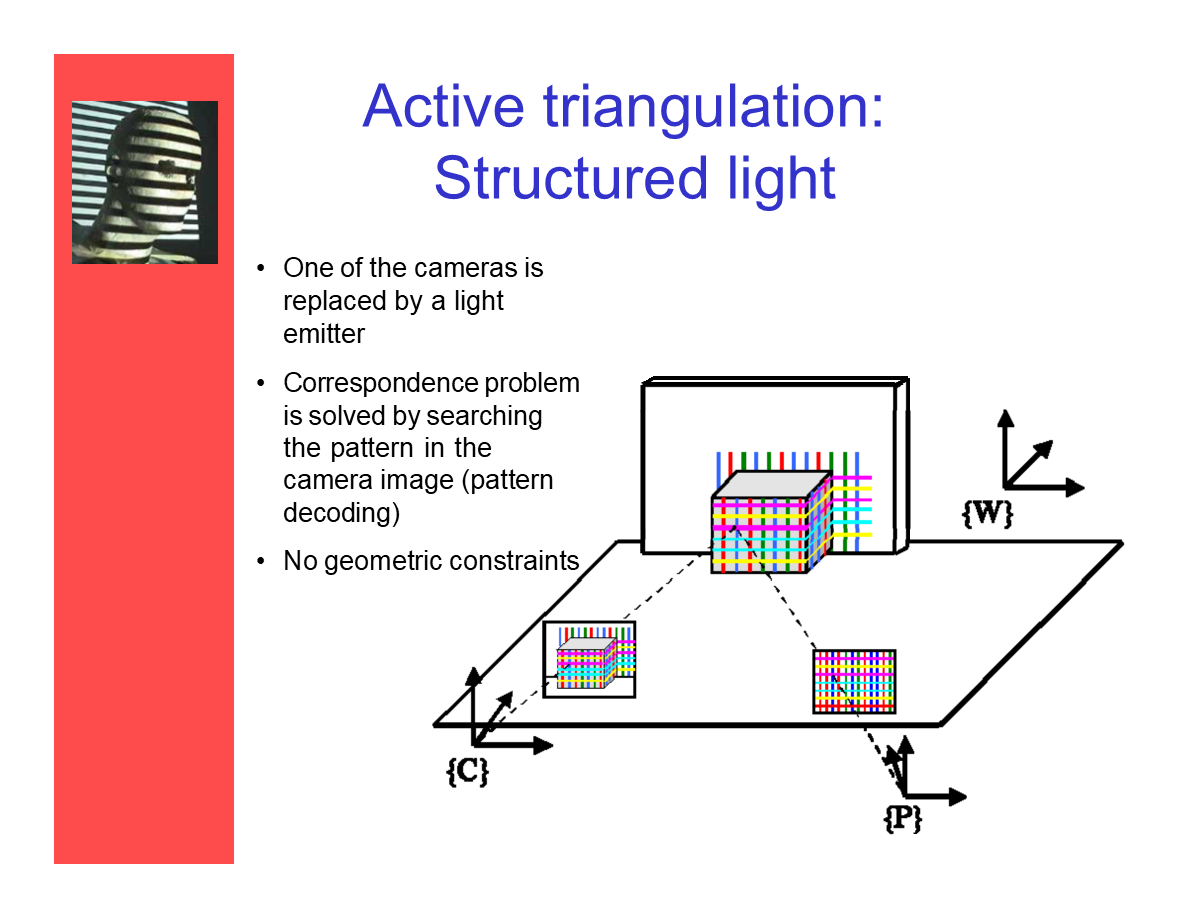
主动三角测量：结构光

其中一个摄像机被光投射器代替。
对应点问题被转化为在摄像机对应图像中进行纹样查找的问题（纹样解码）。
没有几何约束。

概述

*从概述来看，这部分内容我按逻辑接近程度拆成了4节。

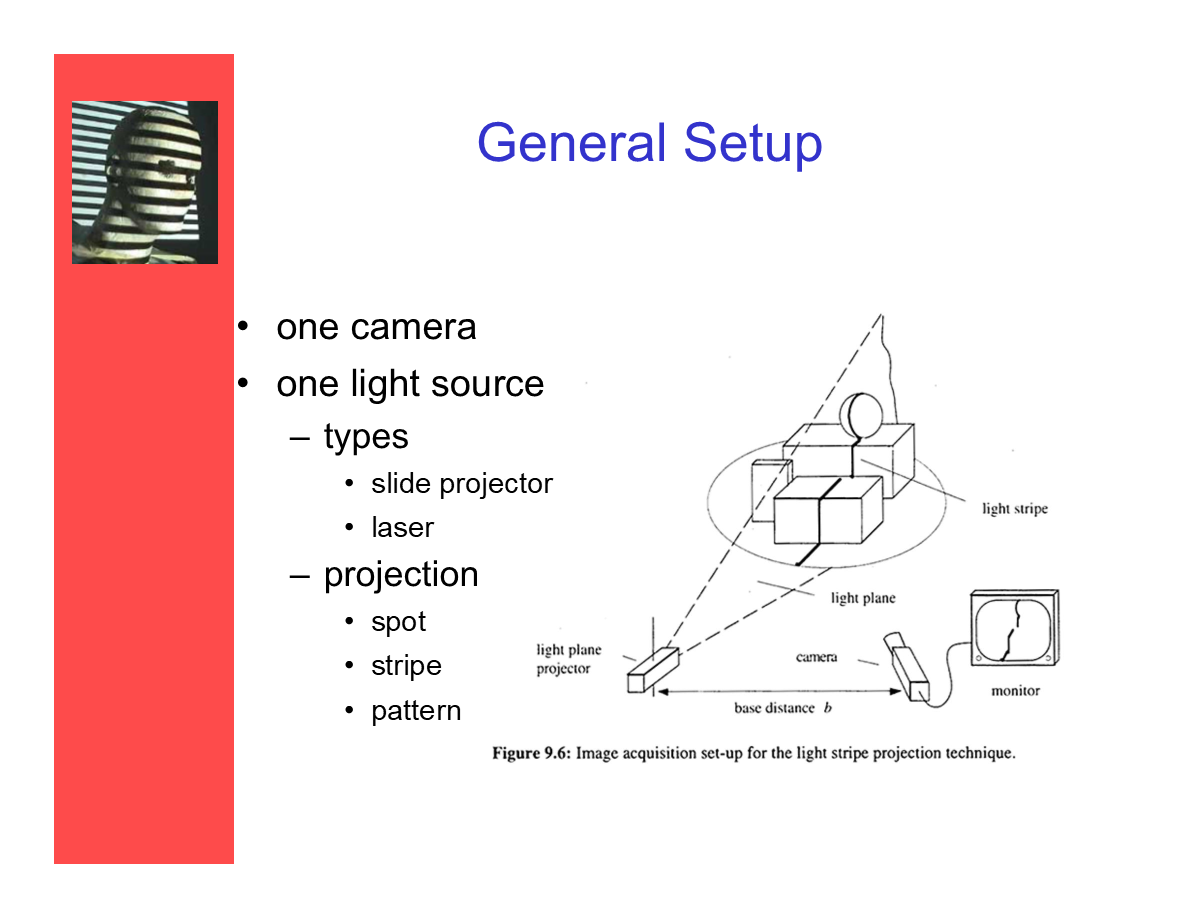
基础设置

一个摄像机。

一个光源：

——类型：滑动投射器；激光。
——投射：点；带状；纹样。

二、光点投影

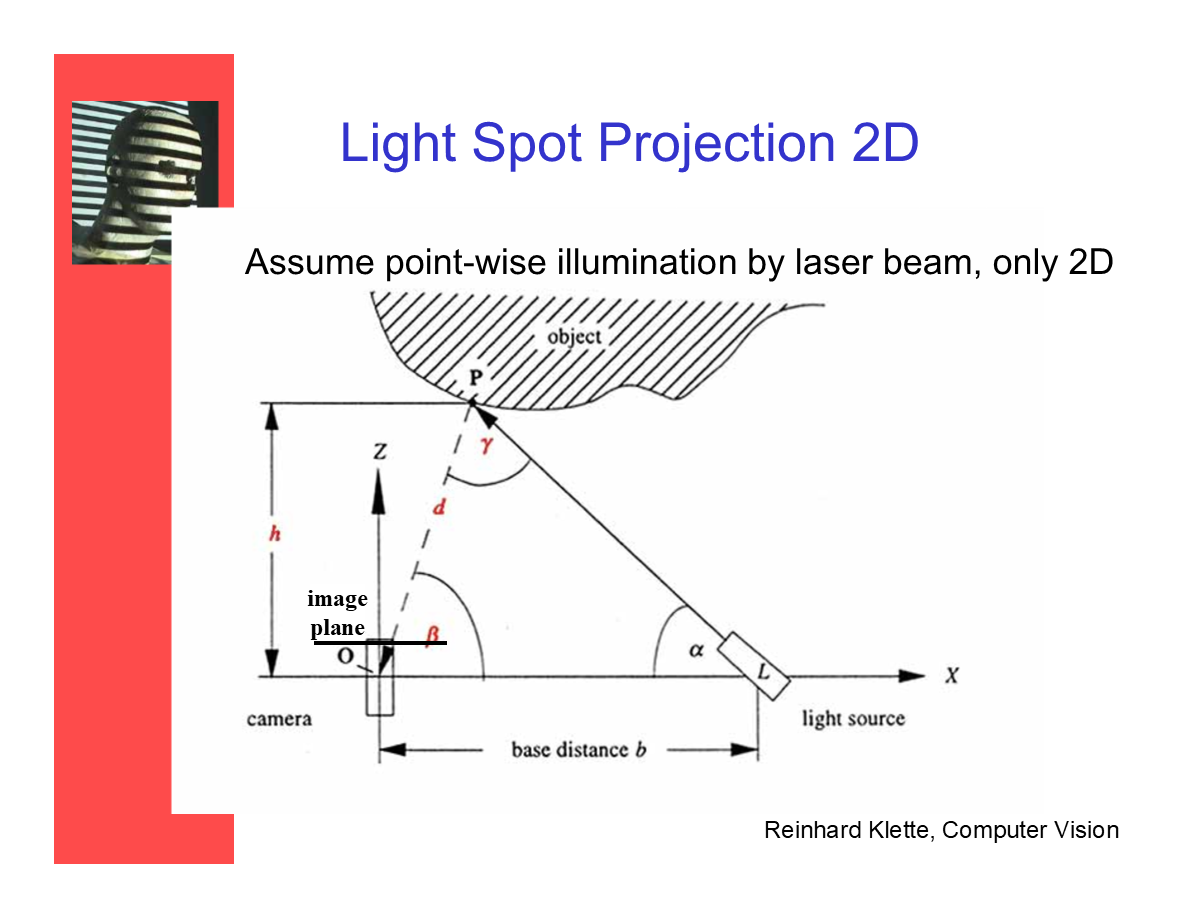
2D光点投射

假设激光束在2D平面上进行逐点式照明。（即设备只考虑水平距离及旋转，接收设备视为一个线段而不是平面）

O、L和P点定义了一个三角形，并且我们通过三角测量确认了P点的（空间）位置——使用了如图中公式的基础三角函数sine法则。

通过三角测量可得出的坐标：

β可以通过（摄像机）投影几何得出。
d值的计算（见图中公式）。
P的坐标用X0，Z0表示——分别可以用d与β的三角函数计算出。

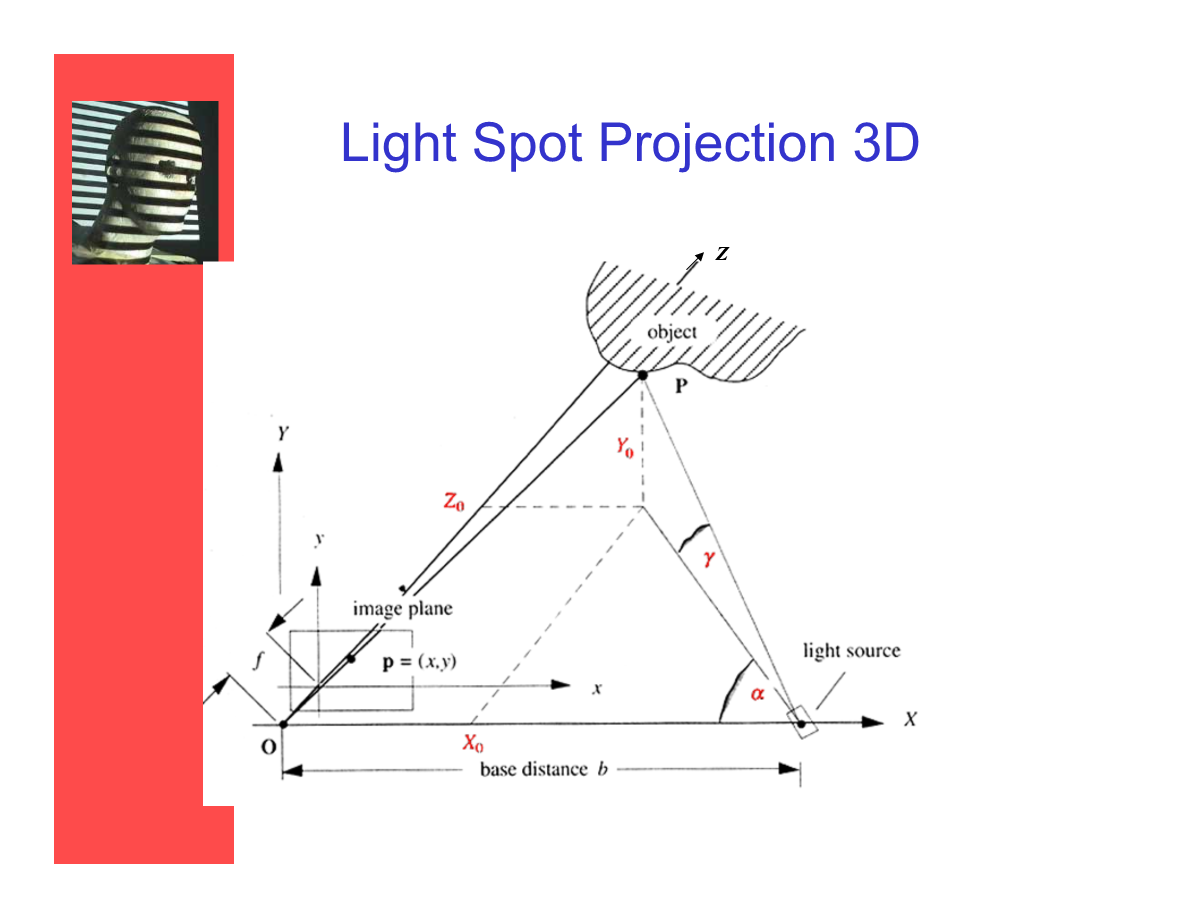
3D光点投射

*3维的情况引入了y轴，接收投影的变成了平面——投影点p位于该平面上。

*发射角度上，除了水平角α，还引入了垂直角γ。

*这里在设备设置后，α和b都是已知给定的。

*根据中心点投射的射线定理（ray theorem）——P点的坐标XZY和xfy成正比，其中xy是投影平面上的点p的坐标，f是中心点O到投影平面的距离（写作f其实就是焦距）。

*对于XZ平面上的角α来说，tanα = Z / (b - X)。

*结合前面两个结论可以分别推导出XYZ和tanα的关系（如图）。

最终可以根据α、b 、f、x、y分别计算出X0、Y0、Z0。

一个观察，这部分计算中并没有用到垂直角度γ。

*即根据设备基础的位置角度信息，及投影坐标x、y即可计算点P的坐标。

三、光带投影

光带扫描——单条

光学三角测量：

投射单个激光条
用它扫描物体的表面
这是结构光扫描的一个非常准确的版本
利于生成高精度的3D结果，但需要大量的时间以拍摄很多图片

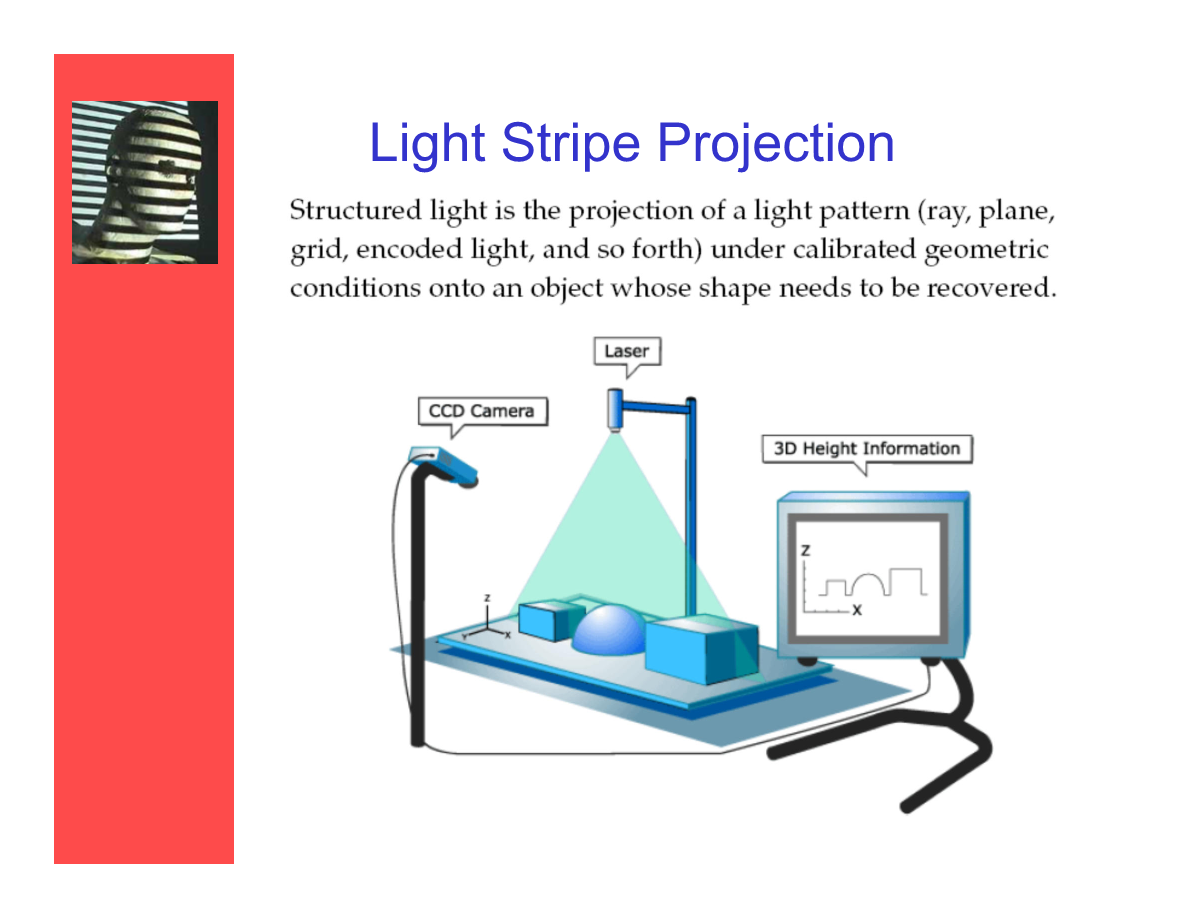
光带投射

结构光方案是——在校准过的几何条件下向目标物体投以一个光纹样（射线、平面、栅格、编码的光源、以及其它），并进行三维重建。

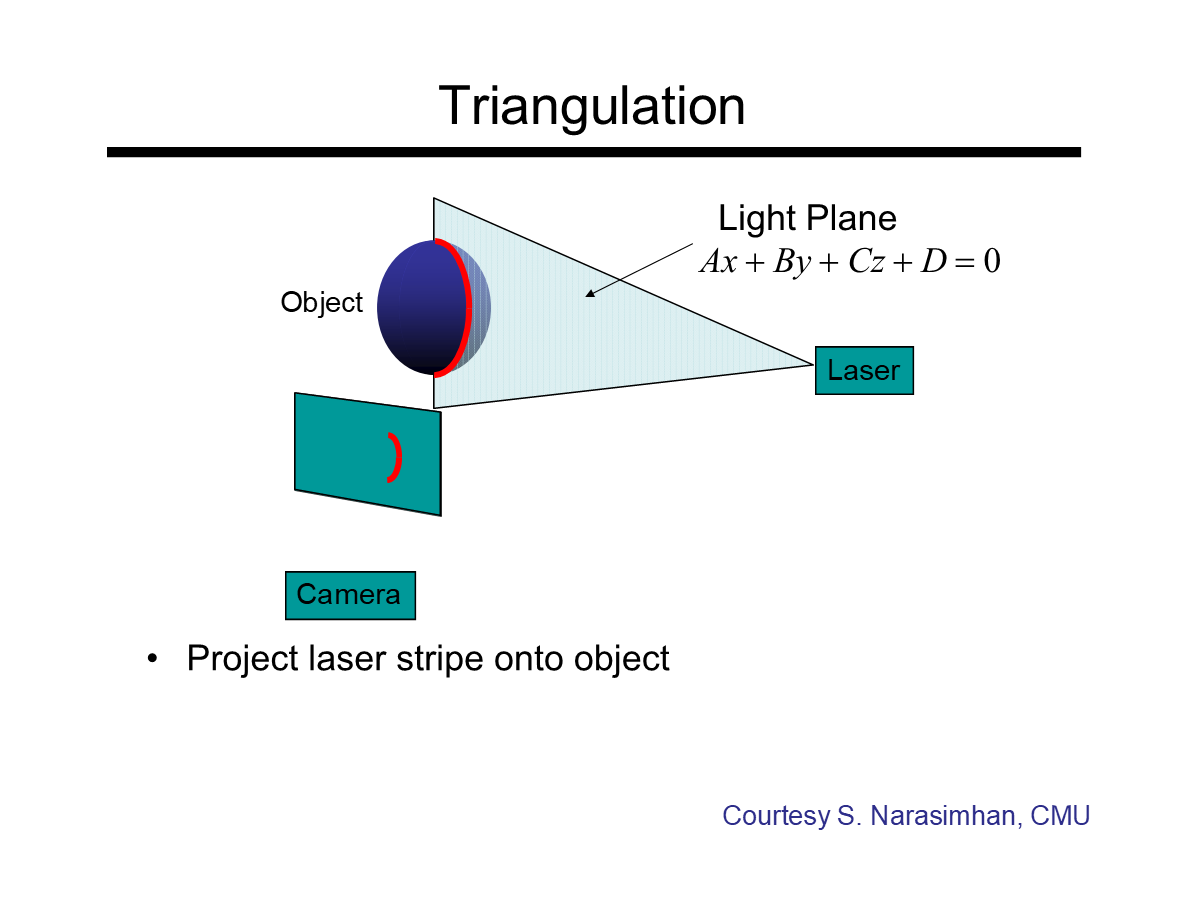
（结构光的）三角测量

*这个案例中激光发射出的是一个“光平面”，它会与物体表面相交投下光带。平面的表达式如图——基于摄像机光学中心为坐标原点。

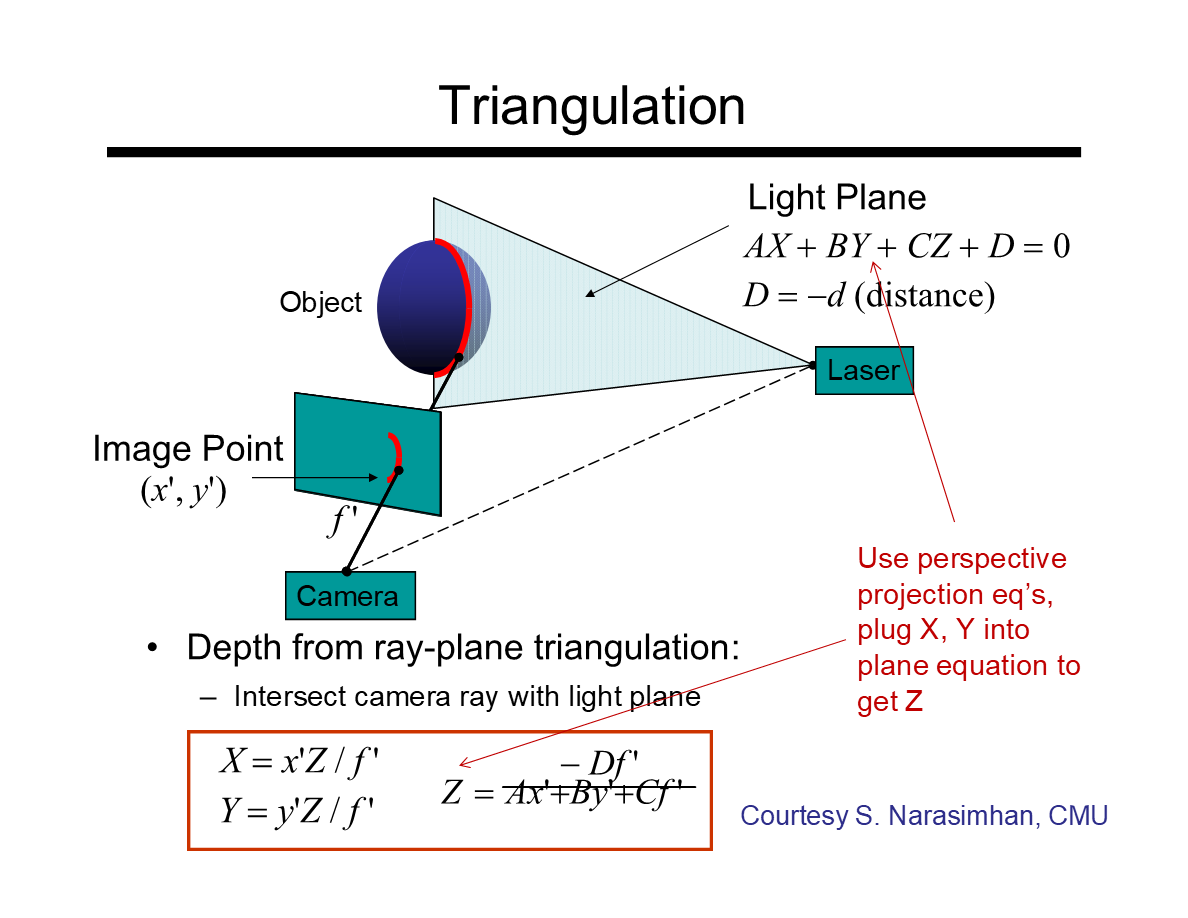
*图中信息较多，这里实际是要在已知一个投影点（x'，y'）及当前投影校准几何相关信息的前提下，计算三维空间的深度——也就是Z值。

*对于一个点的情况，参照前一节提到的单点三维投射：X/x' = Z/f' = Y/y' 的结论仍是成立的，因此可以得到X、Y值基于Z的表达式（如图）。

*D = -d。其中d是光平面到摄像机光学原点的距离。因为平面方程中ABC的几何意义是平面的法向量，D可以理解成将平面移到坐标原点的距离。

*将已知的x'、y'、f'、D、A、B带入公式即可得出Z值（如图）。在这种坐标设置下，Z值就是物体上的点相对于摄像机的深度值。

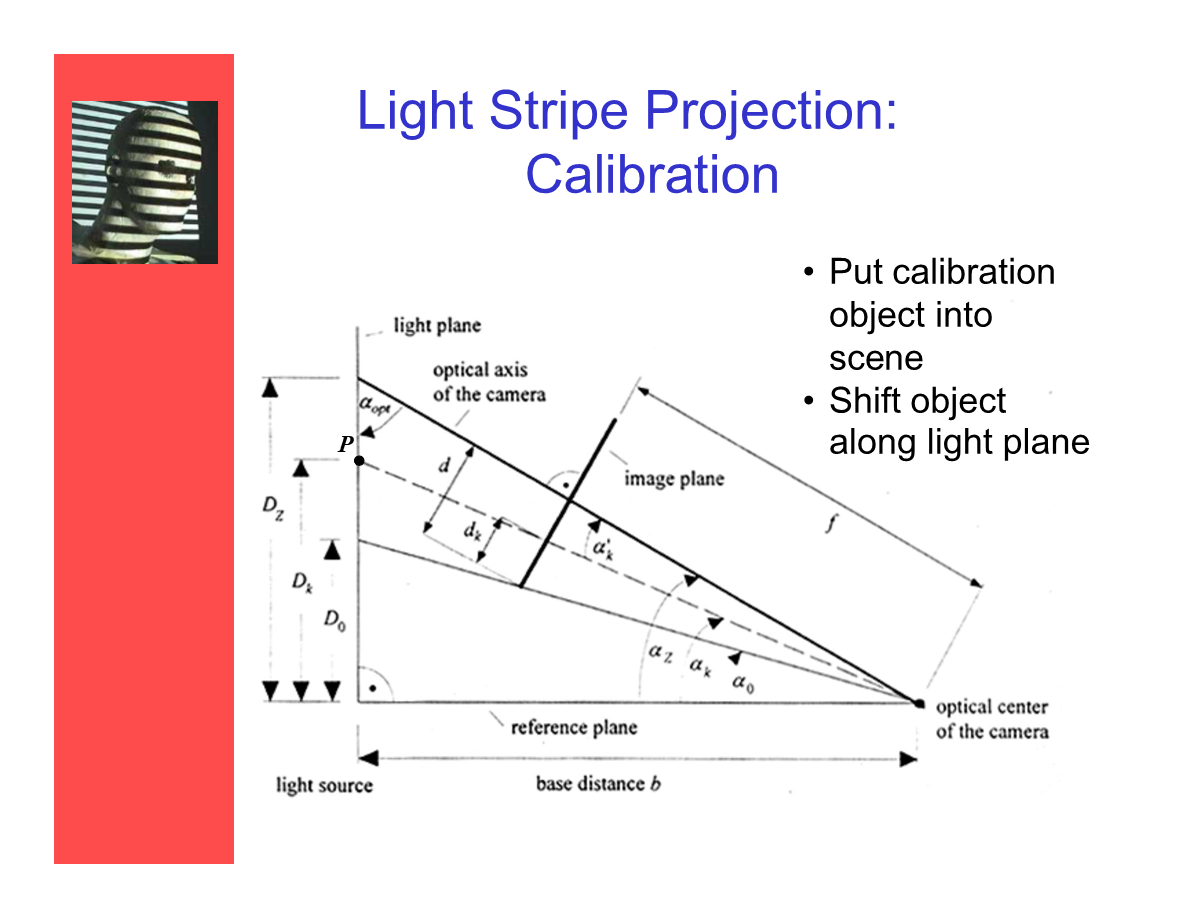
光条投射——校正

将校正物体放入场景，并沿着光平面平移。

*图中从顶视图展示了各个几何关键点的位置关系。通过校准计算可以得出光平面相对于光学原点的平面参数。

距离校正

要校准一个固定光平面的系统的距离，一个简单的方法是假设目标物体在一个“转盘”上，其旋转中心是光平面的原点。

校准平面在两点——max和min之间移动，与光平面平行。在最大值处，（摄像机的）图像中最右侧的列会被照亮，在最小值处则是照亮最左侧的值。对于每一列y我们测量其在光学平面的Z值，这就是满足y列被照亮的校准平面的坐标值。

*这部分直接翻译理解上可能有点抽象，其实旋转和距离是两个关切点。结合后面的例图应该更好理解一些。

更直接的方法：单条光带与旋转物体

转盘上的物体：

对每一个旋转位置和光窄口（slit）创建对应的轮廓P（X,Y,Z）。
以离散的间隔旋转物体，并重复这一过程。
以柱面方式集成轮廓信息，以重建3D物体——以3D网格的方式。

*注意这里的多条纹是集成后的结果。

示例：激光扫描器

优点：非常精确，误差在0.01毫米以内。

缺点：需要10秒以上时间完成一次扫描。

便携式3D激光扫描器示例

四、3D拍摄与其它轻量级的方案

基于阴影的3D信息获取

*这里列出了这一节讨论的内容的论文出处，有兴趣的可以按需搜索。

你桌边的3D拍摄工具

使用常规工具以“便宜”的方案进行3D拍摄。
需要：PC、摄像机、棍子、台灯、棋盘板。
使用“弱结构光”方案。

设备设置示意图

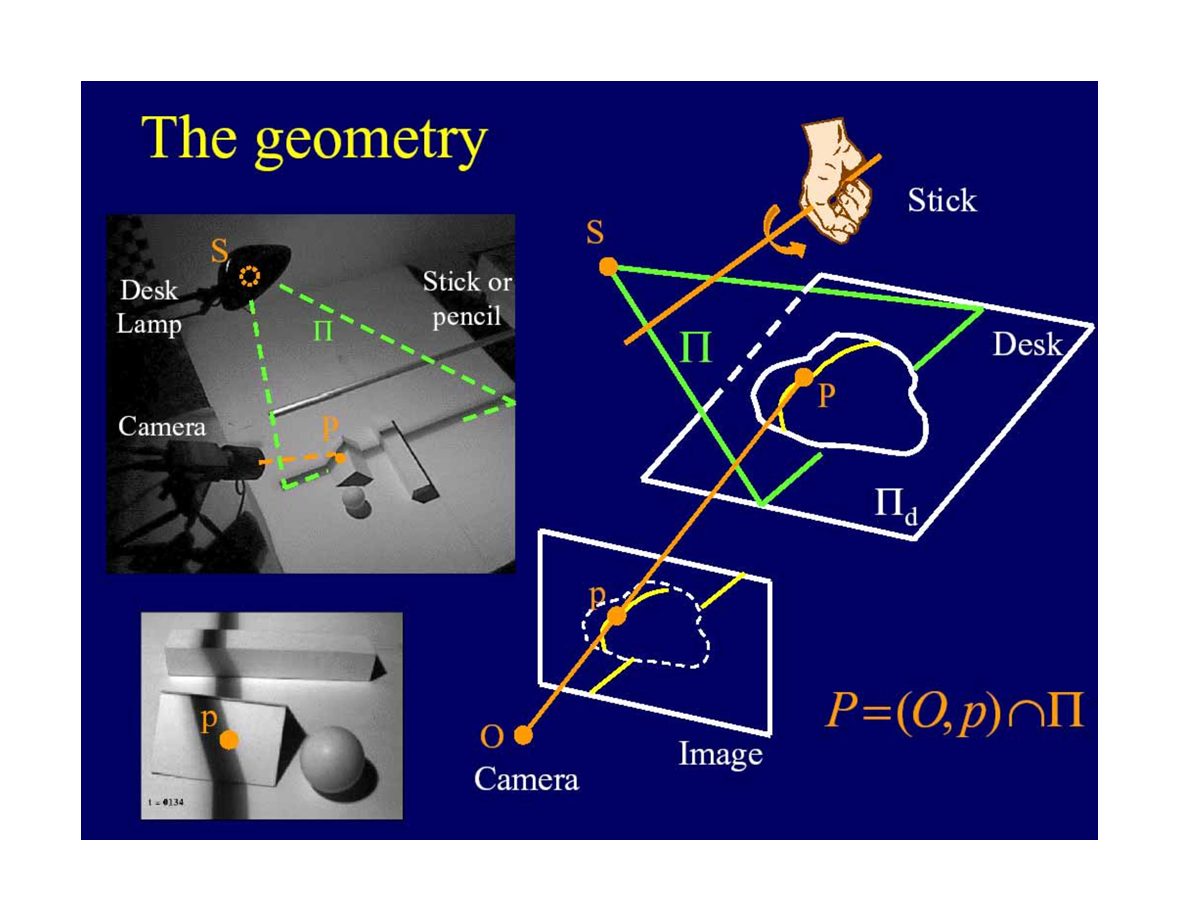
*可以看到，这里的棍子的阴影起到了之前光带的作用。

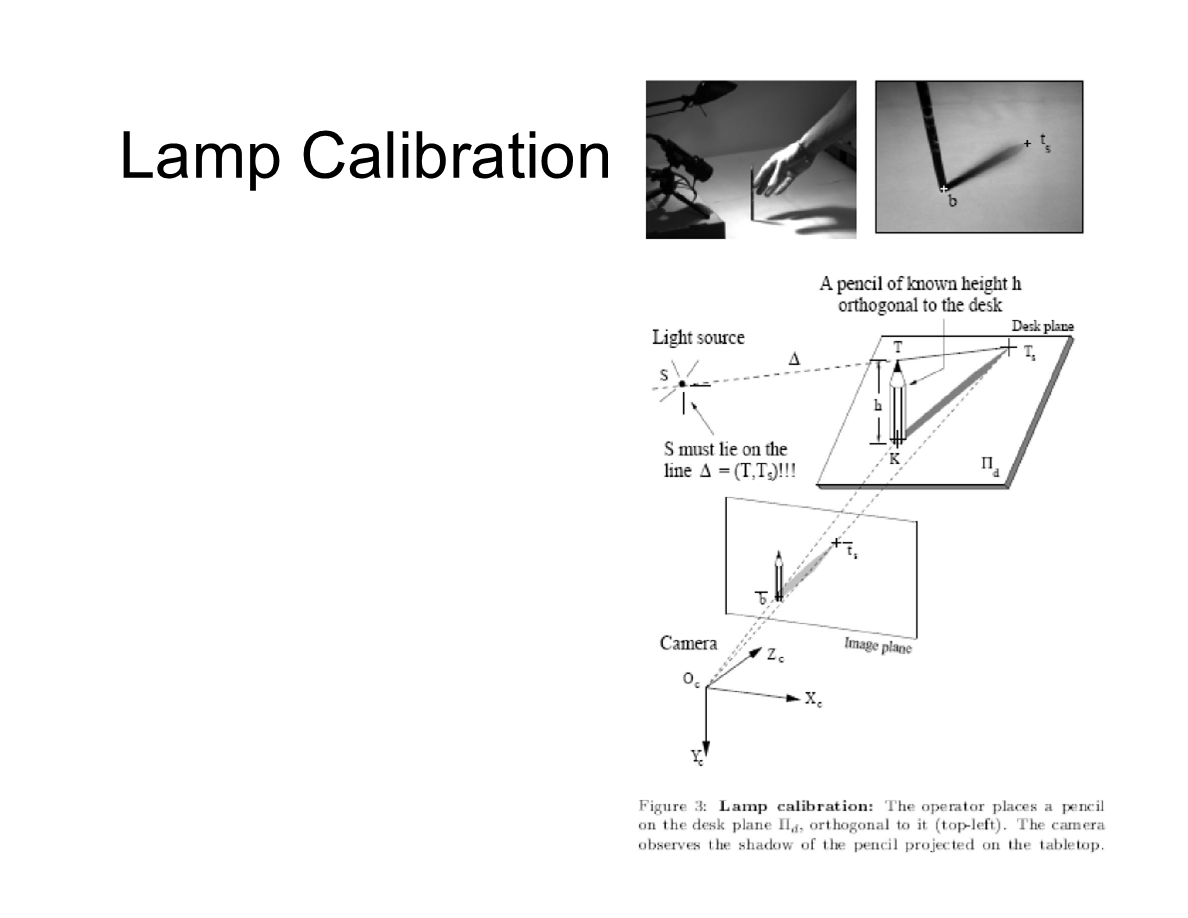
台灯校准

台灯校准：操作者在桌面放置了一根铅笔，与其垂直。在摄像机中观测铅笔在桌面投下的阴影。光源中心S需要在T和Ts的延长线上。

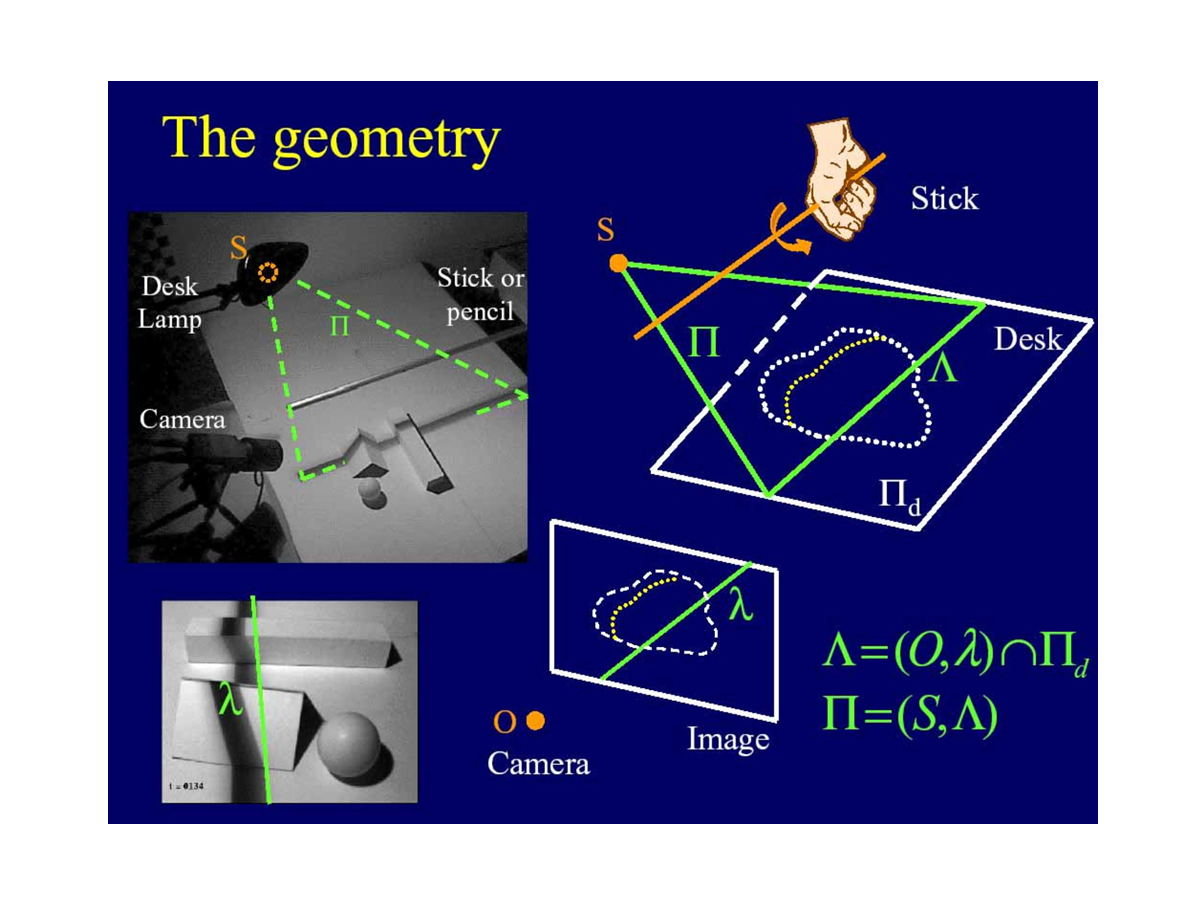
当棍子与桌面平行时

* ∩ 是相交的符号， Λ 是平面（O， λ）与 Π d的相交直线。

*Π是由S和Λ确定的平面。在确定了“人造光平面”后，问题就转化为了前一节解决的问题。

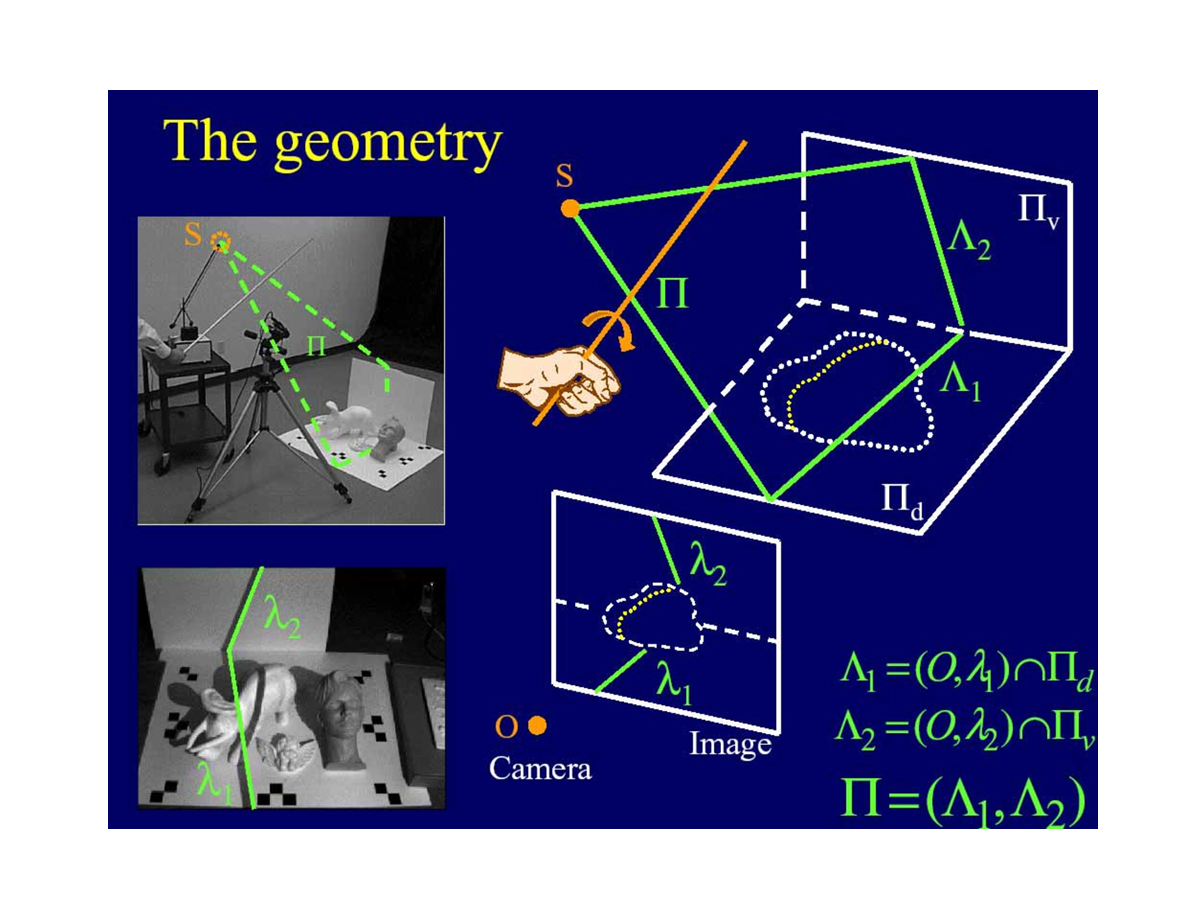
当棍子与桌面有角度时

*这里额外引入了一个平面和一根线，最终用两条相交线确认了平面Π 。推导方式和前一页原理相同。

天使实验

*从图中可以看出，这种方法误差是0.1%，但也有一些位置信息不能很好的确定——和阴影宽度有关。

基于日光的扫描

*图中虽然是黑白的，但是主要思路是用细棍在车身投影。误差是 0.5% 。

大家都能使用的低成本3D扫描器

*从图中可以看出扫描小物体需要的设备尺寸及扫描情况。

*图中是2009年的一篇SIG文章，其中介绍了包括结构光在内的一些常见的3D扫描技术。

结语

通过粗读这篇课件，我们了解了结构光方案作为一项“主动”方案在确定性及便捷性上的优点。在本篇的最后停在了光带（或人造阴影条）进行扫描测量的部分，涉及的计算没有超出立体几何的范围。

这个系列两篇文章的下一篇会介绍以“编码纹样”进行结构光扫描的方案（Pattern encoding/decoding），相对会更难理解一些，但确实也是提升结构光方案效率的必经之路。

下面是资料链接：

Structured Lighting Guido Gerig CS 6320, 3D Computer Vision Spring 2015