本文的第一部分
本文的第二部分
形式系統的缺陷·跳出系統的嘗試
數學家希爾伯特(David Hilbert)曾經說過:
“如果連數學思維都有缺陷,我們還能在哪裡找到真理與確定呢?”
從亞里士多德的三段論與歐幾里得的幾何學,再到喬治·布爾的邏輯運算與德·摩根的演繹推理,數學家與邏輯學家都無比堅信數理邏輯的客觀性與準確性,將推理的思維過程加以機械化的嘗試也在進行。

歐幾里得
但十九世紀與二十世紀數學上的發現卻提出了新的挑戰:非歐幾里得幾何學採用了與現實世界截然不同的“點”“線”概念,它對“數學是研究現實世界的”觀點表達了質疑。數論在每個可想象的世界裡都是相同的嗎?如果不是相同的,那支配所有數論的“元數論”是怎麼樣的呢?除此之外,還有由集合論中的悖論引發的“第三次數學危機”。最著名的是羅素悖論(antinomy of Russell,即理髮師悖論):
一個集合自身是這個集合中的元素嗎?
如果一個人聲明自己是“無法被定義的”,那麼TA就會被定義成“無法被定義的”。這些悖論似乎都發生於一個系統指涉自身時,它們將我們熟知的數學變成了一個怪圈,一個難以走出的迷宮。
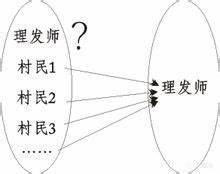
那個悖論中的理髮師該給自己理髮嗎?
數學與邏輯是緊密交織的,如果能在嚴密的邏輯推理中導出所有的“真理”數學,就能避免像羅素悖論那樣的矛盾,這就是希爾伯特《數學原理》一書想要達到的目的。如果能用邏輯推理與配數(將一組命題符號串轉化成一組數字,從而找到某種同構關係)的方法,找到一個對數論一致性與或完全性的證明(《GEB》中寫道,所謂一致性,是每個定理經過解釋後都變成真的;所謂完全性,是指每個真的且可表示成符號串的陳述都是定理),就能重新穩固這座悖論之上搖擺的數學大廈。

如果你接觸過考公,你就肯定會學到翻譯推理
希爾伯特希望利用數學系統本身中的一小部分方法來證明整個數學系統是正確的,從而避免“如何使用自己的推理方法來證明自己所用的推理方法是正確的?”這類循環論證的、無止境的悖論問題。也許這種方法可以理解成“只使用2、3、5、7…質數有關的理論,來證明1、2、3、4、5…所有自然數有關的理論的正確性”,可以說這是一個人拽著自己的鞋帶來提起自身離開地面的嘗試。
大衛·希爾伯特
然而,庫爾特·哥德爾,在1931年發表了他的論文《論數學原理及有關係統中形式上不可判定的命題》,徹底粉碎了希爾伯特的美好願望。論文指出,一旦對一個形式系統進行了哥德爾配數,把形式系統轉化成同構的數論進行研究,就能找到一種指向自身的數論陳述,類似“說謊者悖論”的情況就會發生。如果只使用數學系統中的方法來證明數學系統的一致性,那麼它本身就會是不一致的!類似的,完全性也被推翻了。任何自洽的形式系統,如果它強大到包含基本運算,那麼它的內部就會有這樣的悖論命題。《GEB》中對於這部分的探討持續了數個大章節,在這裡實在難以用簡單的寥寥幾句來概括。
關於哥德爾不完備定理的證明,可以看B站上UP畢導的這個視頻《這個視頻裡說的都是真的,但你卻永遠無法證明》:
視頻鏈接
能填補這個漏洞嗎?為何不將這個漏洞作為一個定理加入到形式系統中去呢?《GEB》認為,這是一種無力的嘗試,形式系統本身有能進行自我指涉的性質,使得你只能無限生成一層接一層的漏洞,這是一種本質上的不完全性,你無法逃脫這個形式系統的制約,就像本文開頭的例子一樣。這種銜尾蛇般吞下自身的嘗試是無意義的。《GEB》還提到,原本的推導方式只用到了自然數,但如果要填補這個形式系統的漏洞,就必須有諸如無理數、虛數之類的“超自然數”引入,就像歐幾里得幾何學朝非歐幾何學的方向擴充一樣,引入了原本系統之外的東西!而這些東西是原本系統無法涉及的東西!
銜尾蛇,一種古代的圖騰,一種吞下自身的嘗試
哥德爾不完備定理的存在,似乎說明了機械編碼的計算機永遠無法模仿人類智能。如果將巴比奇的差分機探進它自己的內部,是否就能產生機械化的智能呢?然而只要它是機器,就對應於一個形式系統,從而就能在自我指涉中生產出一個哥德爾過程來證明自己的不完備性,機器的矛盾就此產生了。這樣的機械本質上來說是“死”的,而心智是“活”的,這看起來是對於人類靈魂存在的一個無可辯駁的證明。可如果這個證明是真的,那今天“ChatGPT”等高級人工智能的出現又如何解釋呢?作者指出,這種證明假設計算機知曉的東西和我們人類一樣多,而我們總能在計算機這個系統外面實施哥德爾運算來證明不完備性。
埃舍爾《龍》
但是計算機受制於自己的系統,它知曉的東西不可能和我們一樣多!在系統外面,我們能發現這個系統的漏洞具體是什麼,但系統裡面,即使它可能知道自己有一個漏洞,但它找不到漏洞具體是什麼,甚至可能對漏洞毫無察覺。就像埃舍爾的上面這幅作品《龍》一樣,平面的龍極力想從二維空間掙扎出來,變成三維生物。但不論怎麼看似精妙的嘗試,都無法讓它跳脫出二維空間這一系統的限制。英國作家埃德溫·艾勃特(Edwin·A.·Abbott)的《平面國》也有類似的內容。一個系統自我指涉的哥德爾化能力是有限度的,智能是有限度的,但它不一定就不能被模仿與複製。
克萊因瓶。當然三維空間的我們不可能真正製造出這種高緯度的物體
一個被精心編碼的計算機程序看似能夠修改自身,實則不能違背自身最底層的指令。回到我們人類自身,我們的智能也是受限的,無法跳出某種根本制約它的系統。與埃舍爾筆下的龍類似,我們永遠無法在三維空間中造出真正的彭羅斯階梯,抑或是克萊因瓶,永遠只能造出它們在三維空間的投影。從生物機理來說,人類看不到大多數波長上的顏色,也聽不到大多數頻率上的聲音;我們瞭解世界,又必須依賴神經系統的中介,而它總會制約我們所感受到的“真實”。
《合金裝備5·幻痛》。遊戲中的“聲帶蟲”能感染並殺死使用特定語言的人,進而毀滅使用那個語言的文明
又聯想到語言學中的“薩丕爾—沃爾夫假說”,我們的心智或者思維,是否都被我們所使用的語言所決定?法國精神分析家雅克·拉康(Jacques Lacan)說過:
“符號是人和物的不在場。語言是對人和物的殺戮。”
我們使用語言,用語言談論語言,卻不能跳出語言(符號界)這個系統去涉及它之外的東西(實在界)。
雅克·拉康。如果你經常瀏覽B站的哲學區,你就會頻繁看到他的名字
如何超越自我,跳出人類自身?這是一個現代的神話。法國哲學家米歇爾·福柯(Michel·Foucault)一生中就不斷通過藥物濫用、同性虐戀等方式來追尋“極限體驗”與“個人主體的消解”,前往非理性的一面,從而重新審視自我與世界。這種叛經離道的行為貫穿了他的整個哲學研究生涯。《GEB》中也提到了禪宗這一宗教走出自身的嘗試,即“加深一個人的自我意識,拓展系統的範圍,最終與宇宙相一致。”但也許,這些超越自我的嘗試,都只是發現自身有限性的那些人服用的安慰劑罷了。
關於米歇爾·福柯的一張meme圖
(未完待續)