本文的第一部分
本文的第二部分
形式系统的缺陷·跳出系统的尝试
数学家希尔伯特(David Hilbert)曾经说过:
“如果连数学思维都有缺陷,我们还能在哪里找到真理与确定呢?”
从亚里士多德的三段论与欧几里得的几何学,再到乔治·布尔的逻辑运算与德·摩根的演绎推理,数学家与逻辑学家都无比坚信数理逻辑的客观性与准确性,将推理的思维过程加以机械化的尝试也在进行。

欧几里得
但十九世纪与二十世纪数学上的发现却提出了新的挑战:非欧几里得几何学采用了与现实世界截然不同的“点”“线”概念,它对“数学是研究现实世界的”观点表达了质疑。数论在每个可想象的世界里都是相同的吗?如果不是相同的,那支配所有数论的“元数论”是怎么样的呢?除此之外,还有由集合论中的悖论引发的“第三次数学危机”。最著名的是罗素悖论(antinomy of Russell,即理发师悖论):
一个集合自身是这个集合中的元素吗?
如果一个人声明自己是“无法被定义的”,那么TA就会被定义成“无法被定义的”。这些悖论似乎都发生于一个系统指涉自身时,它们将我们熟知的数学变成了一个怪圈,一个难以走出的迷宫。
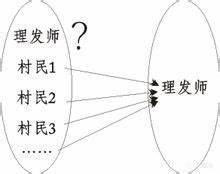
那个悖论中的理发师该给自己理发吗?
数学与逻辑是紧密交织的,如果能在严密的逻辑推理中导出所有的“真理”数学,就能避免像罗素悖论那样的矛盾,这就是希尔伯特《数学原理》一书想要达到的目的。如果能用逻辑推理与配数(将一组命题符号串转化成一组数字,从而找到某种同构关系)的方法,找到一个对数论一致性与或完全性的证明(《GEB》中写道,所谓一致性,是每个定理经过解释后都变成真的;所谓完全性,是指每个真的且可表示成符号串的陈述都是定理),就能重新稳固这座悖论之上摇摆的数学大厦。

如果你接触过考公,你就肯定会学到翻译推理
希尔伯特希望利用数学系统本身中的一小部分方法来证明整个数学系统是正确的,从而避免“如何使用自己的推理方法来证明自己所用的推理方法是正确的?”这类循环论证的、无止境的悖论问题。也许这种方法可以理解成“只使用2、3、5、7…质数有关的理论,来证明1、2、3、4、5…所有自然数有关的理论的正确性”,可以说这是一个人拽着自己的鞋带来提起自身离开地面的尝试。
大卫·希尔伯特
然而,库尔特·哥德尔,在1931年发表了他的论文《论数学原理及有关系统中形式上不可判定的命题》,彻底粉碎了希尔伯特的美好愿望。论文指出,一旦对一个形式系统进行了哥德尔配数,把形式系统转化成同构的数论进行研究,就能找到一种指向自身的数论陈述,类似“说谎者悖论”的情况就会发生。如果只使用数学系统中的方法来证明数学系统的一致性,那么它本身就会是不一致的!类似的,完全性也被推翻了。任何自洽的形式系统,如果它强大到包含基本运算,那么它的内部就会有这样的悖论命题。《GEB》中对于这部分的探讨持续了数个大章节,在这里实在难以用简单的寥寥几句来概括。
关于哥德尔不完备定理的证明,可以看B站上UP毕导的这个视频《这个视频里说的都是真的,但你却永远无法证明》:
视频链接
能填补这个漏洞吗?为何不将这个漏洞作为一个定理加入到形式系统中去呢?《GEB》认为,这是一种无力的尝试,形式系统本身有能进行自我指涉的性质,使得你只能无限生成一层接一层的漏洞,这是一种本质上的不完全性,你无法逃脱这个形式系统的制约,就像本文开头的例子一样。这种衔尾蛇般吞下自身的尝试是无意义的。《GEB》还提到,原本的推导方式只用到了自然数,但如果要填补这个形式系统的漏洞,就必须有诸如无理数、虚数之类的“超自然数”引入,就像欧几里得几何学朝非欧几何学的方向扩充一样,引入了原本系统之外的东西!而这些东西是原本系统无法涉及的东西!
衔尾蛇,一种古代的图腾,一种吞下自身的尝试
哥德尔不完备定理的存在,似乎说明了机械编码的计算机永远无法模仿人类智能。如果将巴比奇的差分机探进它自己的内部,是否就能产生机械化的智能呢?然而只要它是机器,就对应于一个形式系统,从而就能在自我指涉中生产出一个哥德尔过程来证明自己的不完备性,机器的矛盾就此产生了。这样的机械本质上来说是“死”的,而心智是“活”的,这看起来是对于人类灵魂存在的一个无可辩驳的证明。可如果这个证明是真的,那今天“ChatGPT”等高级人工智能的出现又如何解释呢?作者指出,这种证明假设计算机知晓的东西和我们人类一样多,而我们总能在计算机这个系统外面实施哥德尔运算来证明不完备性。
埃舍尔《龙》
但是计算机受制于自己的系统,它知晓的东西不可能和我们一样多!在系统外面,我们能发现这个系统的漏洞具体是什么,但系统里面,即使它可能知道自己有一个漏洞,但它找不到漏洞具体是什么,甚至可能对漏洞毫无察觉。就像埃舍尔的上面这幅作品《龙》一样,平面的龙极力想从二维空间挣扎出来,变成三维生物。但不论怎么看似精妙的尝试,都无法让它跳脱出二维空间这一系统的限制。英国作家埃德温·艾勃特(Edwin·A.·Abbott)的《平面国》也有类似的内容。一个系统自我指涉的哥德尔化能力是有限度的,智能是有限度的,但它不一定就不能被模仿与复制。
克莱因瓶。当然三维空间的我们不可能真正制造出这种高纬度的物体
一个被精心编码的计算机程序看似能够修改自身,实则不能违背自身最底层的指令。回到我们人类自身,我们的智能也是受限的,无法跳出某种根本制约它的系统。与埃舍尔笔下的龙类似,我们永远无法在三维空间中造出真正的彭罗斯阶梯,抑或是克莱因瓶,永远只能造出它们在三维空间的投影。从生物机理来说,人类看不到大多数波长上的颜色,也听不到大多数频率上的声音;我们了解世界,又必须依赖神经系统的中介,而它总会制约我们所感受到的“真实”。
《合金装备5·幻痛》。游戏中的“声带虫”能感染并杀死使用特定语言的人,进而毁灭使用那个语言的文明
又联想到语言学中的“萨丕尔—沃尔夫假说”,我们的心智或者思维,是否都被我们所使用的语言所决定?法国精神分析家雅克·拉康(Jacques Lacan)说过:
“符号是人和物的不在场。语言是对人和物的杀戮。”
我们使用语言,用语言谈论语言,却不能跳出语言(符号界)这个系统去涉及它之外的东西(实在界)。
雅克·拉康。如果你经常浏览B站的哲学区,你就会频繁看到他的名字
如何超越自我,跳出人类自身?这是一个现代的神话。法国哲学家米歇尔·福柯(Michel·Foucault)一生中就不断通过药物滥用、同性虐恋等方式来追寻“极限体验”与“个人主体的消解”,前往非理性的一面,从而重新审视自我与世界。这种叛经离道的行为贯穿了他的整个哲学研究生涯。《GEB》中也提到了禅宗这一宗教走出自身的尝试,即“加深一个人的自我意识,拓展系统的范围,最终与宇宙相一致。”但也许,这些超越自我的尝试,都只是发现自身有限性的那些人服用的安慰剂罢了。
关于米歇尔·福柯的一张meme图
(未完待续)