一,邻域概念
设p(x,y)是xoy平面上的一个点,e是某一正数。与点p距离小于e的点f的全体,称为点p的e邻域,记作U(p,e)。即:
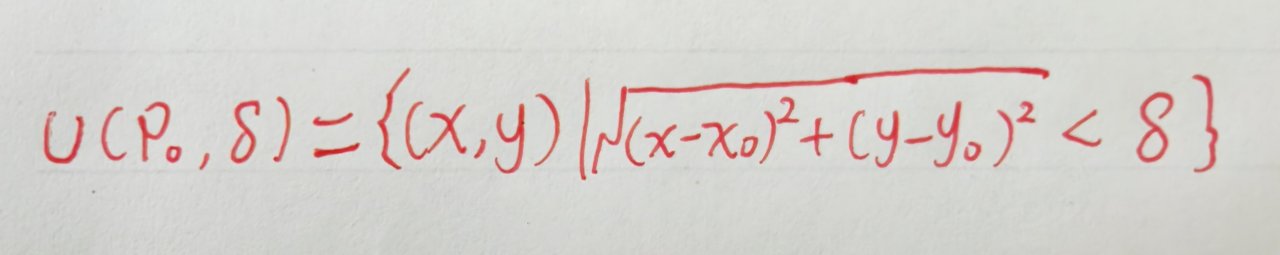
去心邻域是

二,点和点集的关系
(P是点,E是点集)
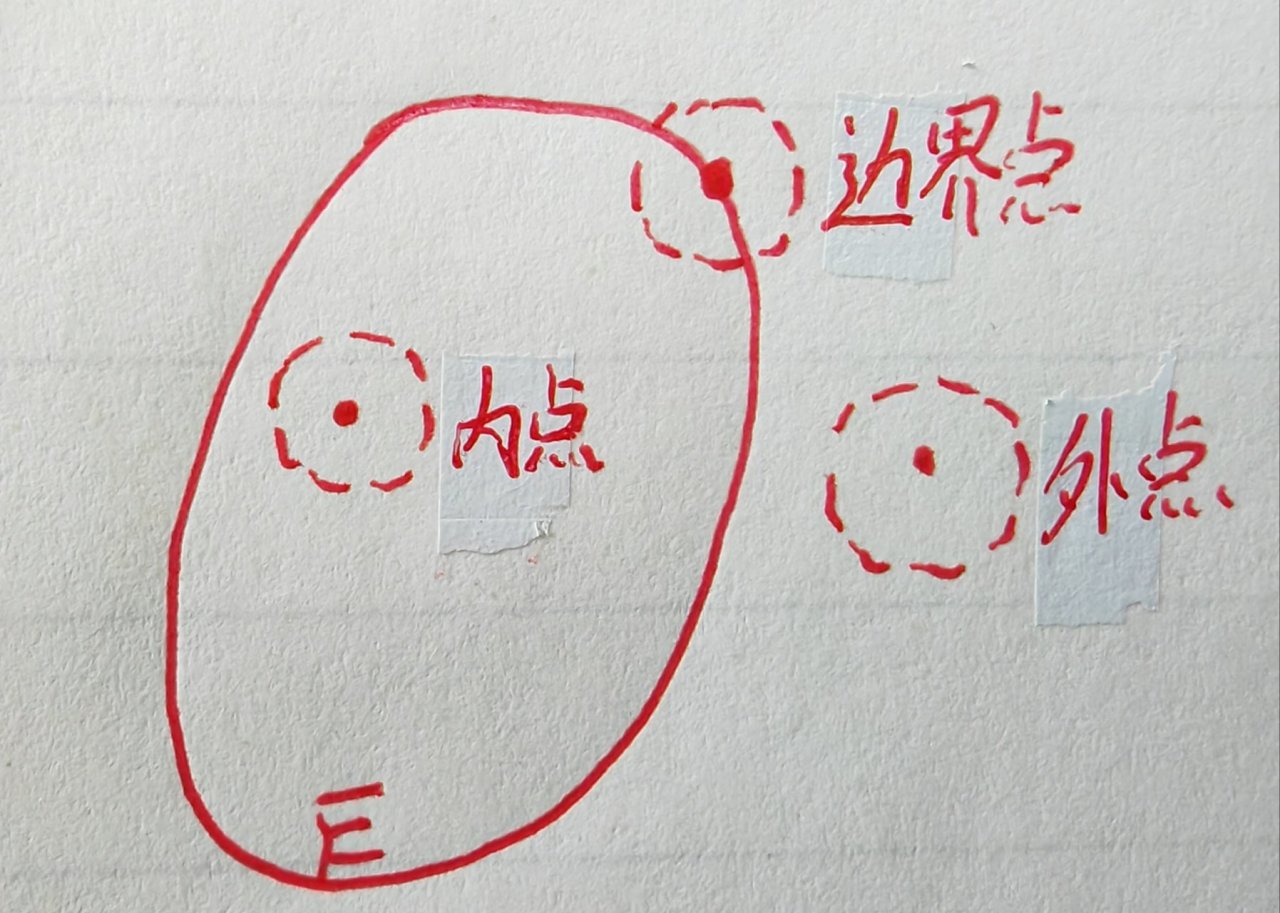
1.内点:P的某个邻域包含在E之中,P为内点。
2.外点:P的某个邻域和E交集为空集,P为外点。
3.交界线:P的任一邻域既有∈E的点,也有不∈E的点,P为交界点。
4.聚点:点P的去心邻域总有E的点,P为聚点。
(所以内点和边界点都为聚点)
注意:
1.之所以内点和外点是“某个”是因为如果邻域过大,条件可能不满足。
2.
三,重要的平面点集
1.开集:点集E的点都是E的内点,即边界∉E。例:
2.闭集:点集E边界∈E。例:
3.连通集:点集E上的任何两点都可以用折线连接起来,且折线上的点∈E。
反例:
4.开区域(区域):连通的开集。
5.闭区域:开区域和它的边界。
注意:不能理解成"连通的闭集"
6.有界集:不趋于无穷,有起始范围。
7无界集:无具体范围。