设 q=我方强度-对方防御，伤害系数为α=f(q)，由图：
f(0)=1, f(150)=2, f(375)=3, f(675)=4, f(1050)=5
f并不容易得到，设 g(α)=q，观察发现，x为大于2的正整数时，g(x)-g(x-1)=75x 。
将其推广至x>0的实数域内，于是有g(x)=37.5(x^2+x+C)，其中C为任意常数，
代入g(1)=0，C=-2，于是g(x)=37.5(x^2+x-2)
经推导，f(x)=sqrt(x/37.5+2.25)-0.5，也就是说：
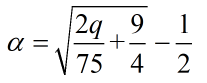
2.强度和伤害的搭配比例
即：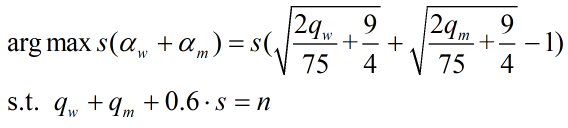
解释下这个0.6咋来的，就小伙伴装备而言，强度的易得性是伤害的0.6倍显然最优时两个q应该相等，不妨就令它们都为q，即：
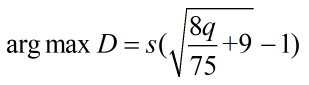在上述的约束条件下，显然：
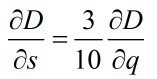即：
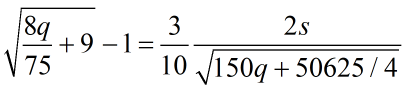所以：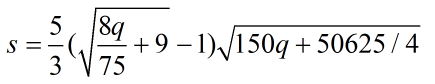
这玩意没法化简了，注意这里的q是 己方物理强度-对方物理防御=己方魔法强度-对方魔法防御 时的 己方强度-对方防御。
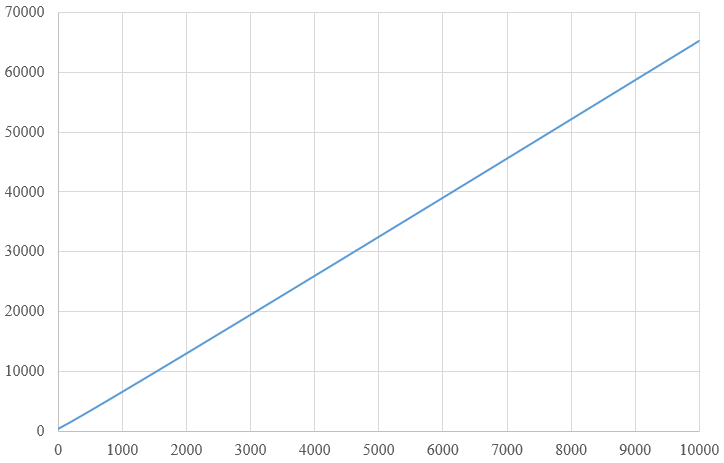它的图像非常非常接近于线性。但是不是线性，不信可以泰勒展开：
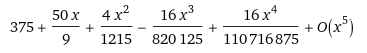作为粗略结论，可以认为 s=6.5 q，没错这结论就是如此朴实无华且枯燥。就这样，没有考虑的东西非常非常多，比如暴击、技能、穿透等等，权且当个参考。