一 前情提要
1.1
1.2
在上篇文章的最後,已經推導出了這個等式:一定量A=一定量B。
①兩邊的能指單元,在自然形式上,均為完全相同的東西。因為能指所表達的意義,才是能指的真正本體,而能指本身,作為自然形式而存在的東西,僅僅只是這個意義本體的替身。能指自身的存在狀況,並不是看自身的自然形式,而是看其所對應的意義是什麼。
②意義不在場,在場的僅僅只有能指本身。因此,在直接的感知呈現上,僅僅只是兩個比賽文本之間的相同關係。
1.3
推導到這一步,問題的關鍵就在於,每一個A和每一個B,各自所對應的意義應該是什麼,才能使得一定量A和一定量B,表達出相同的意義總體。也就是說,在什麼樣的符碼規則下,一定量能指A和一定量能指B,才能表達出相同的意義。
二 簡單形式:一個能指=另一個能指
2.1
兩個一定量能指之間的等同,最基本、最簡單的形式,就是一個能指和另一個能指之間的等同。也就是,兩個單個能指之間的等同。因為對於符號表意活動而言,符號能指在量上的最基本簡單形式,就是一個單獨的能指。
2.11 作為表意性的存在,一定量能指即一個文本,和一個單獨能指,在實質上沒有任何區別。因為一個能指也可以構成文本,單個能指,可以說是文本的最簡單形式。即便文本是由一定量能指構成的,那麼把這整個文本整體,都看作一個不可分的單獨能指,這也是完全可以的,因為能指不是一種自然性存在。
2.12 因此,兩個單個能指之間的等同關係,就成為考察的切入點和出發點。即能指A=能指B。通過探究簡單形式,來進一步地探究整體的表意世界。
2.13 在這裡,還是以100米短跑比賽為例。參賽者A的比賽文本為單個能指A,參賽者B的比賽文本為單個能指B。兩個人的比賽時長相同,均為10秒,即能指A和能指B,表達了相同的比賽結果意義。
2.2
在這裡,每一個能指具體是什麼,取決於它是什麼符號表意活動。例如它是漢語的交流活動,那麼它可能就是一個漢字,也有可能是一個偏旁部首,甚至也有可能是一個韻母單位;如果它是圖畫,那麼它可能就僅僅只是一個小小的色塊而已;如果是競技體育活動,它甚至也可能只是遊戲單位的一個微小動作。總之,符號能指的自然形式,是一個真正無邊無際的領域。任何能夠表達意義的存在,都是符號能指的疆域。
2.21 但是,它與這裡的問題是無關的。這裡的問題,僅僅只是在於,單個能指之間的等同關係,在於這種關係本身。而無論單個能指具體是什麼,都不影響這個關係本身的性質。
2.3
儘管其中每一個能指,其作為能指,就已經在表達著某種意義。但由於意義是不在場的,所以,兩者意義之間的關係,在單個能指當中,並沒有直接表現出來。因此,能指A就只有通過與能指B等同,才能表明:自己與能指B表達著相同的同一個意義。反過來也是如此。
2.31 在這個等式關係中,能指A通過能指B,來表現出自身意義的性質和關係,能指B就成為了這個意義關係的表現材料,而這種材料必然是一種能指。這也就是說,在這個意義關係等式中,能指B成為了一個雙重的能指:一方面,它表達了自身的意義;另一方面,它又表達了A和自己之間的意義等同關係。因此,可以說,它不僅表達了自身的意義,同時也表達了A的意義,從而表達了這個整體的意義關係。
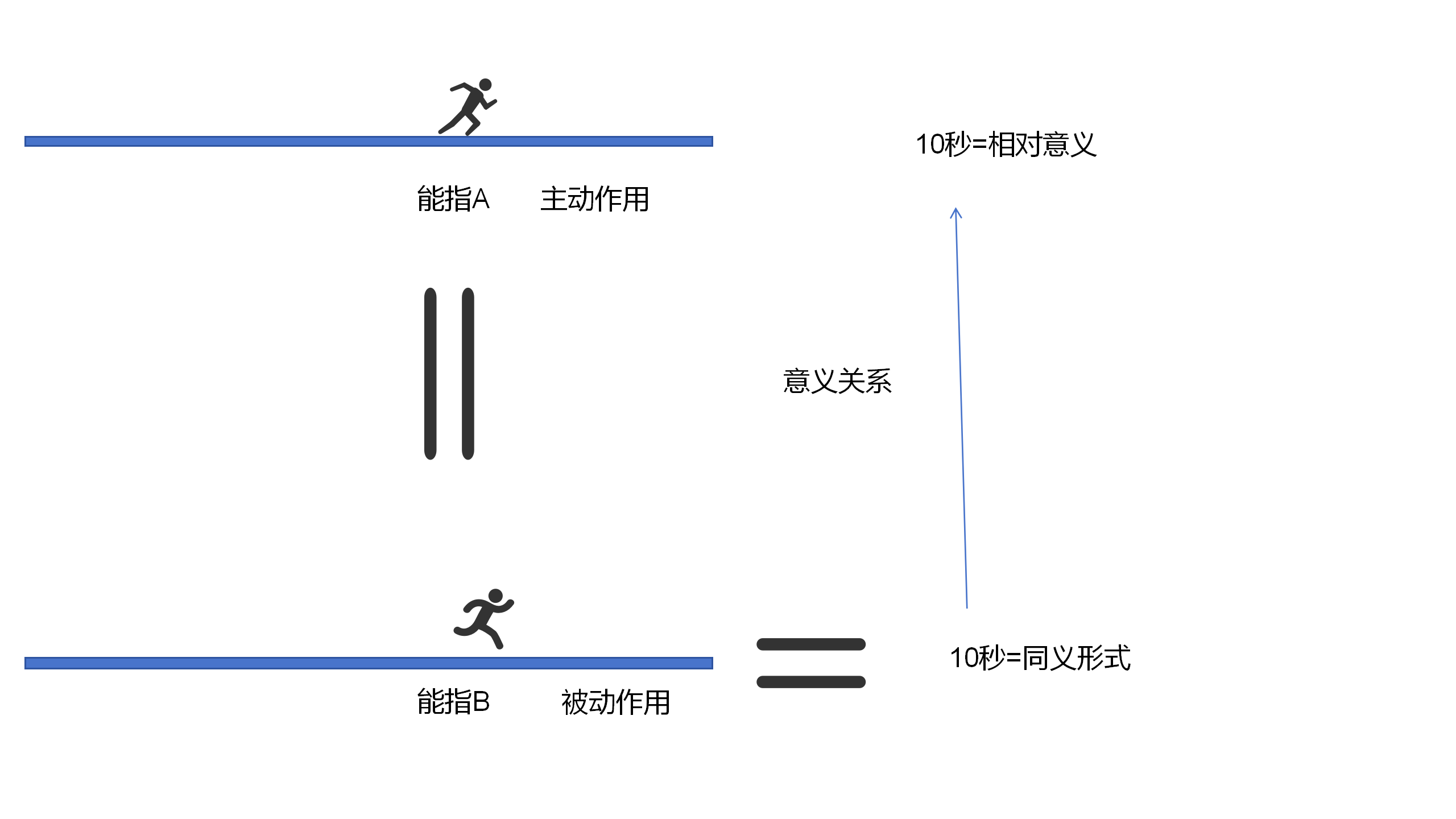
2.32 前一個能指A,起主動作用,後一個能指B,起被動作用。前一個能指A的意義,處於相對性的位置,即相對意義。後一個能指B的意義,起意義等同的作用,處於同義形式。
2.4
這兩個意義形式,是同一個意義等同關係的兩個要素。這兩個要素互相依賴、互為條件、不可分離,同時又是互相排斥、互相對立的兩端即兩極。
通過意義等同關係,兩個不同能指互相發生意義關係,這兩種意義形式,總是分配在這兩個不同能指上面。因為不能用一個能指等同於其自身,來表示一種意義等同關係,這僅僅只是同義反復,裡面沒有任何意義等同關係,這個能指並沒有等同於任何東西。
因此,前一個能指A,其意義的性質和關係,只能相對地表現出來,即通過另一個能指B表現出來。因此,能指A的相對意義,要求有另一個與其相對立的能指B,處於同義形式。因為它不僅表現自身的意義,同時也要表現其他能指的相對意義,也要表現這個意義關係本身。它要提供一種表現材料,來表現其他能指的意義,以及其他能指和自己的意義等同關係。
反過來說,也是如此。能指B=能指A。
2.5
但是,要相對地表現能指B的意義等同關係和性質,就必須把等式倒過來。而這樣一來,能指B的意義就成為了相對意義,而不再是同義形式。
可見,在一個意義等同關係中,同一個能指,不能同時具有兩種意義形式。而且,這兩種形式,是作為兩極而互相排斥的。
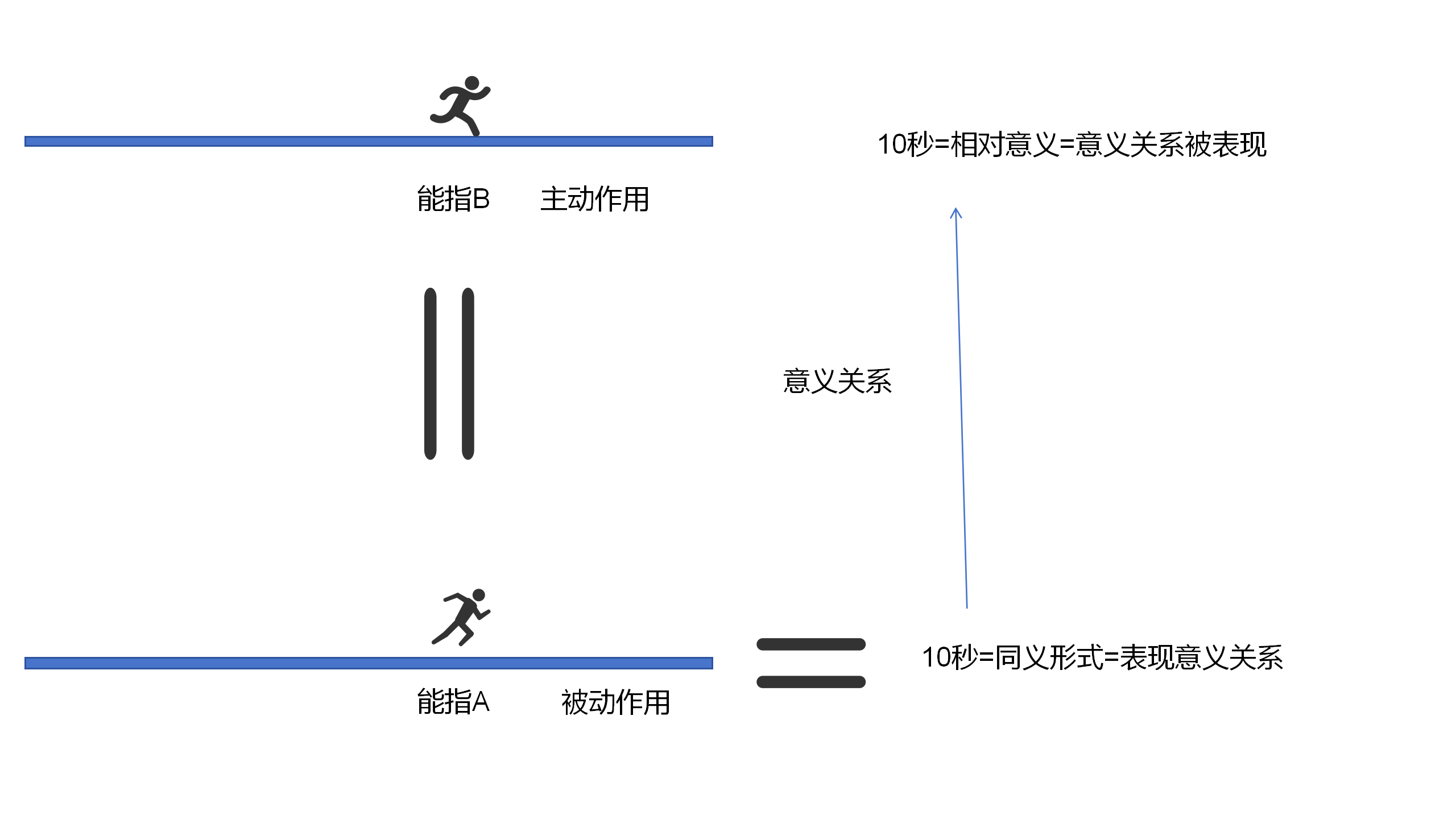
一個能指,究竟是處於相對意義形式,還是處於與之對立的同義形式,完全取決於它在意義等同關係中所處的位置。也就是說,它是意義關係被表現的一方,還是表現意義關係的一方。
三 相對意義→意義關係
3.1
這兩個被看作意義等同的能指,所起的作用是不同的。
只有能指A的意義性質和關係,得到表現。通過與能指B的意義等同關係,把能指B當作它的同義能指。在這個關係中,能指B是這個同一意義的存在形式,因為只有表達了相同的意義,它才是與能指A相同的能指。
另一方面,能指A自身意義的性質得到了獨立的表現,因為能指A只有表達相同的意義,才能把能指B當作相同的東西。
3.2
如果說,一個能指所表達的意義,才是能指的本體,這個能指只是這個意義的替代物。那麼,由於意義本身的不在場,在一場比賽當中,其所有的比賽結果意義之間的意義關係,就還沒有被表現出來,這個意義關係本身,還沒有獲得表現它的能指形式。因為一場比賽至少是2個以上的文本生產者(即參賽者),因而至少有2個以上的文本能指。進而,每一個能指自身意義的性質,也就還沒有被表現出來。
而在一個能指和另一個能指的等同關係中,就不是這樣。兩者的意義等同關係本身,以及在此基礎上的能指自身意義的性質,就通過與另一個能指的關係,而被表現出來。這個意義關係本身,和每一個能指自身意義的性質,就獲得了表現它的能指。
3.3
在能指A的意義等同關係中,能指B是當作與能指A具有相同意義的能指。在這裡,能指B自身,即能指B的自然形式,被當作表現這種相同意義的能指,它以自身的自然形式,表現了兩個能指所共同具有的相同意義,也就是表現了兩個能指的意義等同關係本身,進而也就表達了能指A意義的性質。
在能指A的意義等同關係中,能指B僅僅只是顯示出這一方面,也就是這個相同同一意義的表現,進而是這個等同意義關係的表現。因此,在這個等同關係中,單獨的能指B,就獨自表現了所有能指(A和B自己)的意義,以及所有能指之間的意義關係本身。在這種情況下,能指B的自然形式,似乎就直接呈現出了不在場的同一意義本身,就直接成為了這個同一意義本身即意義關係的直接代表,就成為了純意義的存在。

3.4
可見,能指B成為能指A的同義形式,在這樣的意義關係中,能指B自身的自然形式,就直接成為這個等同關係本身的能指表現。因此,兩者的意義等同關係,以及能指A自身意義的性質,表現在單獨的能指B自身的自然形式上。
作為自然性存在,能指A和能指B分別是完全不同的感知呈現;作為等同的意義,能指A卻是和能指B等同的東西,因而看起來就像能指B。能指A的意義等同關係本身,就這樣就取得了一種自然形式的表現,這種自然形式與能指A自身是不同的自然形式。能指A的意義等同關係和自身意義的性質,就通過它與能指B等同,而表現出來。
3.5
通過意義等同關係,能指B的自然形式,成為了兩者共同意義和意義關係本身的能指形式,成為了反映能指A的意義和兩者意義關係的鏡子。在能指B的自然形式上,這樣表現出來的能指A的意義,具有相對性,是相對意義。
四 同義形式→符碼規則
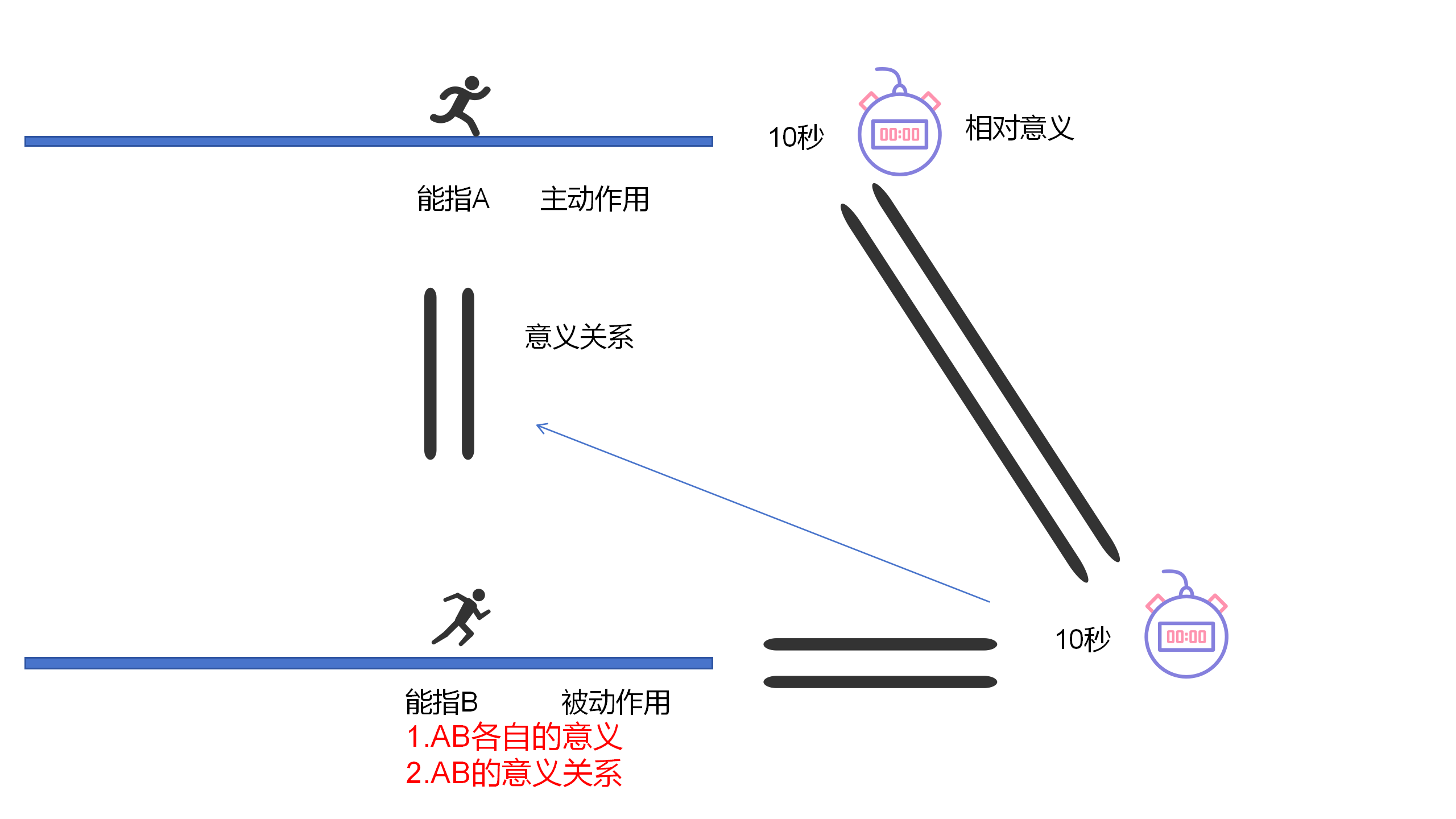
4.1
當能指A通過能指B的自然形式,表現出自身與B的共同意義時,它就使得能指B,取得一種特殊的表意形式,即同義形式。
能指A顯示出自身與能指B的共同意義,是通過兩者的自然形式直接等同。一個能指的同義形式,就是它與另一個能指直接等同的形式。
4.2
同義形式的第一個特點,就是自身的自然形式,成為共同意義關係的表現形式。一個單獨能指的自然形式,成為不同能指之間的意義關係的能指。
但是,對於能指B而言,這種轉換,只有在發生意義等同關係時,即其他能指與它直接等同,只有在這種關係中才能實現。
任何能指,都不能把自身當作同義形式,來同自身發生意義關係,進而也不能用自身來表現自身與自身的意義關係。所以,它必須把另一個能指,當作同義形式,來同它自身發生意義關係。
在能指A的意義關係當中,能指B僅僅只代表兩者的共同意義,和在此基礎上的意義等同關係。

4.3
在這個等同意義關係的背後,同義形式的能指B,有著更為根本性的作用。
也就是說,為什麼這個能指B,能夠成為這樣一個能指,表現了兩者之間的整個意義關係,並進而表現了另一個能指的意義呢?是什麼東西或者機制,使得能指B能夠做到這一點呢?
4.4
前文所說,決定不同能指之間關係的東西,純粹只是與其相對應的意義是什麼,是怎樣的,純粹只是意義對應關係本身。也就是說,能指所表達的意義,才是能指的真正本體,而作為自然形式而存在的能指本身,僅僅只是這個意義本體的替身。
4.5 那麼,再來看這個等式:能指A=能指B。
如果這兩個能指,還沒有被設定為能指,即沒有對應於一個意義,那麼它們就僅僅只是兩個不同的自然形式:自然形式A、自然形式B。在這裡,由於不表意,因此也根本不存在所謂的等同關係。它們僅僅只是兩個互不相干的自然存在。
4.6
這時,B的跑步運動過程,與一個意義X,即10秒的時長,進行對應等同。那麼,B就轉化為了一個表意的能指,表達了這個意義X。那麼自然形式B就被設定為了能指B。
然後,A的跑步運動過程,與能指B進行了等同。通過這種等同關係,自然形式A也就與能指B的意義X,進行了對應等同。進而,自然形式A也就獲得了意義X,它也就轉化為了一個表意的能指,表達了這個意義X,自然形式A,就被設定為了能指B。
由此,能指A就和能指B發生了意義等同關係,能指A=能指B。能指B就作為同義形式,表現了兩者之間的意義關係,以及能指A意義的性質。
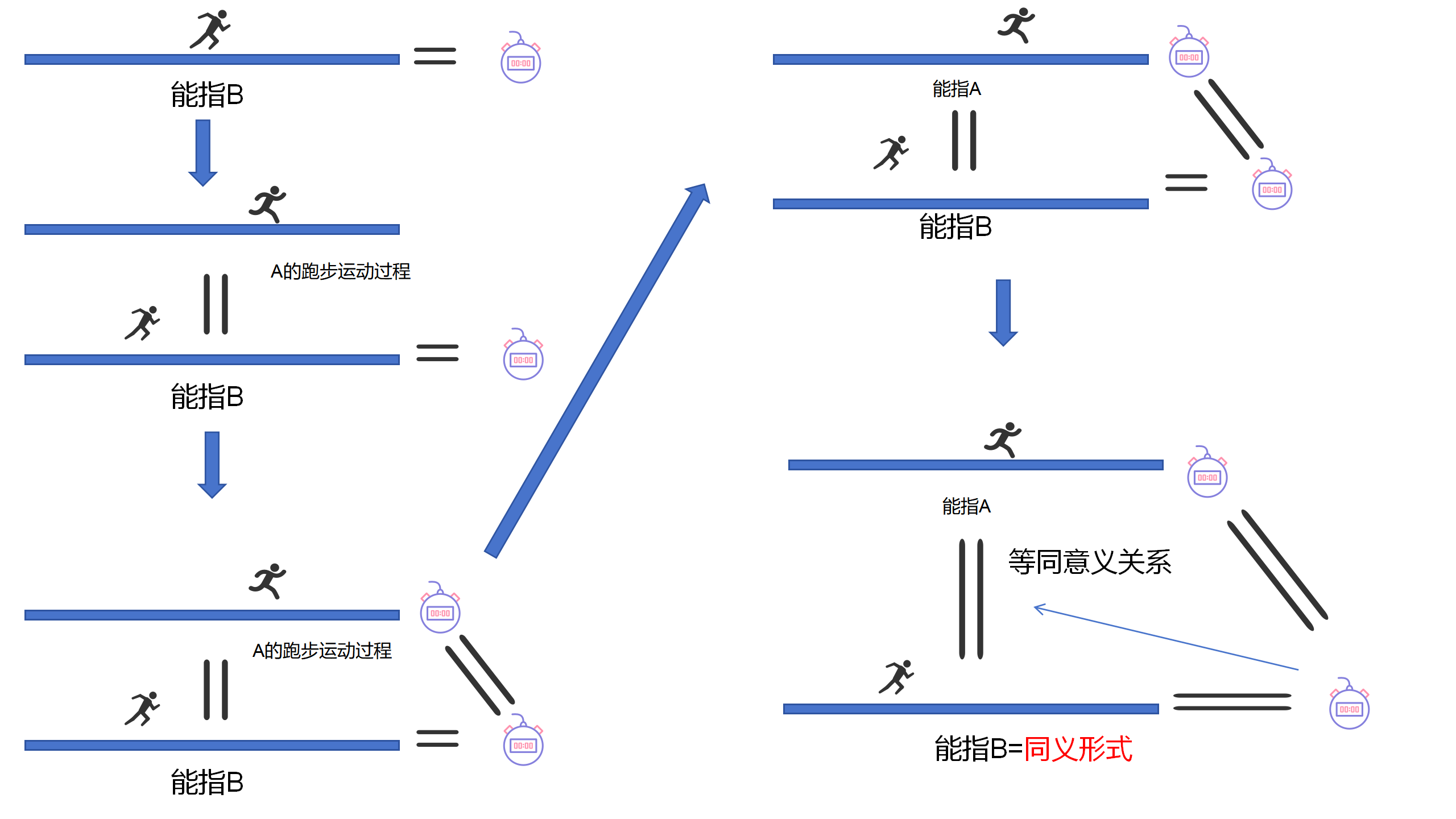
4.7
在這個過程中,B先是與一個意義X進行了對應等同,從而產生了一個意義對應關係。
然後,通過與B等同,A也就與意義X進行了對應等同。因為X是B的本體,因此A=B,實際上就是A=X。
4.8 如果結合前面所說的2個理論:
①符號能指和意義之間的對應關係,就是表意的符碼規則。
②對一個能指進行意義解釋,就是把這個能指和這個意義,進行對應等同。
4.81 那麼,從能指A的視角來看,A=B,就是對A進行了意義解釋。因為A=B,實質上就是讓A=意義X,也就是把A與意義X進行對應等同。
4.82 而A=B之所以能夠做到這一點,是因為已經預先設定了B=意義X,已經預先設定了B的意義對應關係。因此,A等同的,並不是一個單獨的B本身,而是一個整體的意義對應關係。即A=【B=X】。
4.83 因此,是B=X這個意義對應關係,對A進行了意義解釋。
4.84 而意義解釋之所以可能,之所以能夠把能指和意義對應等同,正是因為依據了預先存在的對應等同關係。這個對應關係本身,就是預先存在的符碼規則。
4.85 而既然是B=X讓A能夠等同於X。那麼,對於A而言,B=X這個預先設定的對應等同關係,就形成了A的符碼規則。它使得能指A與意義X之間進行對應等同,A=X,從而把A設定為表達意義X的能指A。
在這裡,A和B之所以能夠實現直接的轉換,直接從B=X轉換到A=X,正是在於:意義才是能指的本體。因此,只要是表達相同的同一個意義,那麼這裡的能指,在自然形式上是A還是B,是無所謂的。

4.9
如果把這個單獨的等式,看作是一個獨立的表意領域,那麼對於這個獨立的表意領域而言,B=X,就是這個領域的符碼規則。
由此可見,同義形式,實際上就是一個表意領域中的符碼規則。它解釋著這個領域中所有其他能指的意義。意義關係的簡單形式,就是最為簡單的一種表意領域;而處於簡單形式中的同義形式,也就是最為簡單的一種符碼規則。
4.91 可以說,相對意義,是被解釋的意義;而同義意義,是進行意義解釋的意義規則。
五 簡單形式的總體
5.1
一看就知道,這種簡單形式是不充分的。
因為兩個能指之間的意義等同關係,僅僅只是表現了兩個參賽者之間的比賽結果關係。而在某些遊戲的比賽中,在整個賽事系列中,參賽者就絕不僅僅只是2個。
5.11 在跑步比賽中,往往是2個以上的賽跑選手;在牌類比賽中,參賽選手往往也是2個以上。即便是單場比賽只有2個參賽者的競技遊戲,如果放眼整個賽事系列,那麼所涉及的比賽結果之間的意義關係,也絕對是超過2個了。

5.2
能指A的意義關係,表現在另一個能指B上面,僅僅只是表現了一個能指的意義關係。因此,也只是使得能指A,同一個其他的能指,發生意義關係。而不是表現能指A,同其他一切能指的意義關係。
與一個能指A的簡單相對意義形式相適應的,是能指B的個別同義形式,也就是單個的個別符碼規則。所以,在能指A的相對意義表現中,能指B只是對能指A 這一個能指來說,具有直接等同的同義形式。
5.3
然而個別的意義關係形式,個別的符碼規則,會自行過渡到更完全的形式。通過個別的意義關係形式,能指A的意義關係,固然只是表現在一個其他能指上,但是這後一個能指,不論是什麼,都完全一樣。
隨著同一個能指A,和各種不同的能指,發生等同意義關係,也就產生種種不同的意義關係形式,也就產生種種不同的符碼規則,即A的意義關係形式和符碼規則。能指A可能有的意義關係和符碼規則,只受到其他能指的數目的限制,其他能指均與能指A不同。
這樣一來,能指A的個別意義關係和個別符碼規則,就轉化為個別關係和符碼規則的一個系列,這個系列可以不斷延長,系列中的每一個個別都是彼此不同的。
六 總和、擴大的意義關係→無限符碼規則
6.1
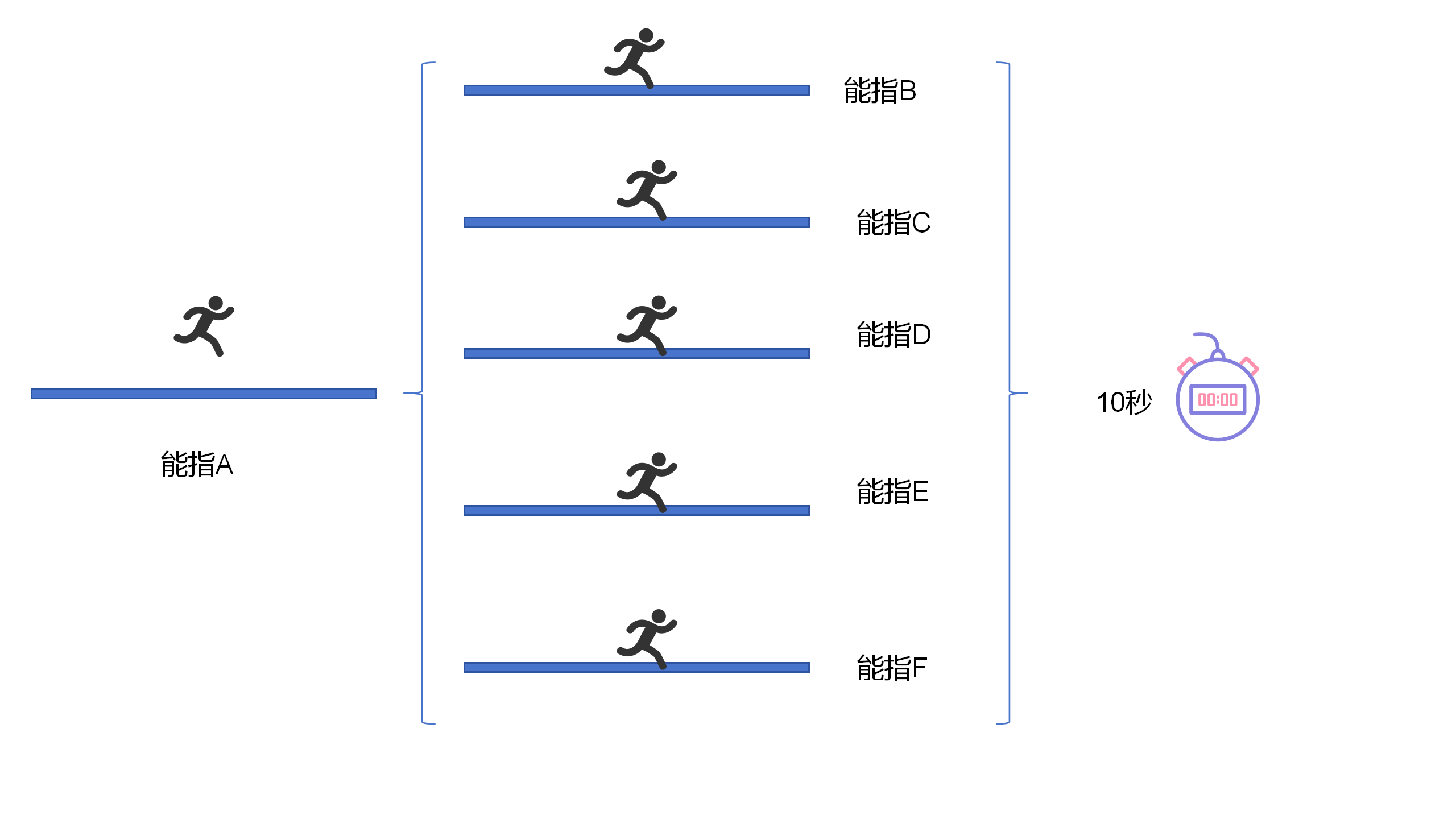
6.2擴大的相對意義形式
現在,一個能指A的意義關係,表現在其他無數的能指上。每一個其他的能指,都成為反映能指A意義性質和意義關係的鏡子。因此,現在能指A通過自己的意義關係形式,不再只同另一個能指發生意義關係,而是同整個能指世界,發生意義關係。作為一個能指,它是這個世界的一個公民。同時,這個等同關係的無限系列表明,能指的意義,和用來表現這種意義的自然形式,是沒有關係的。
6.3
在第一種簡單形式,這兩個能指能夠表達一個相同的意義,可能是偶然的事情。相反,在第二種形式中,一個根本不同於偶然現象,並且決定著這種偶然現象的背景,馬上就顯露出來了。能指A的意義關係,無論是表現在哪個其他能指上,總是等同的意義關係,總是表達著共同的同一個意義。兩個能指之間的偶然關係消失了。顯然,有一個統一的東西,在調節著這一切。
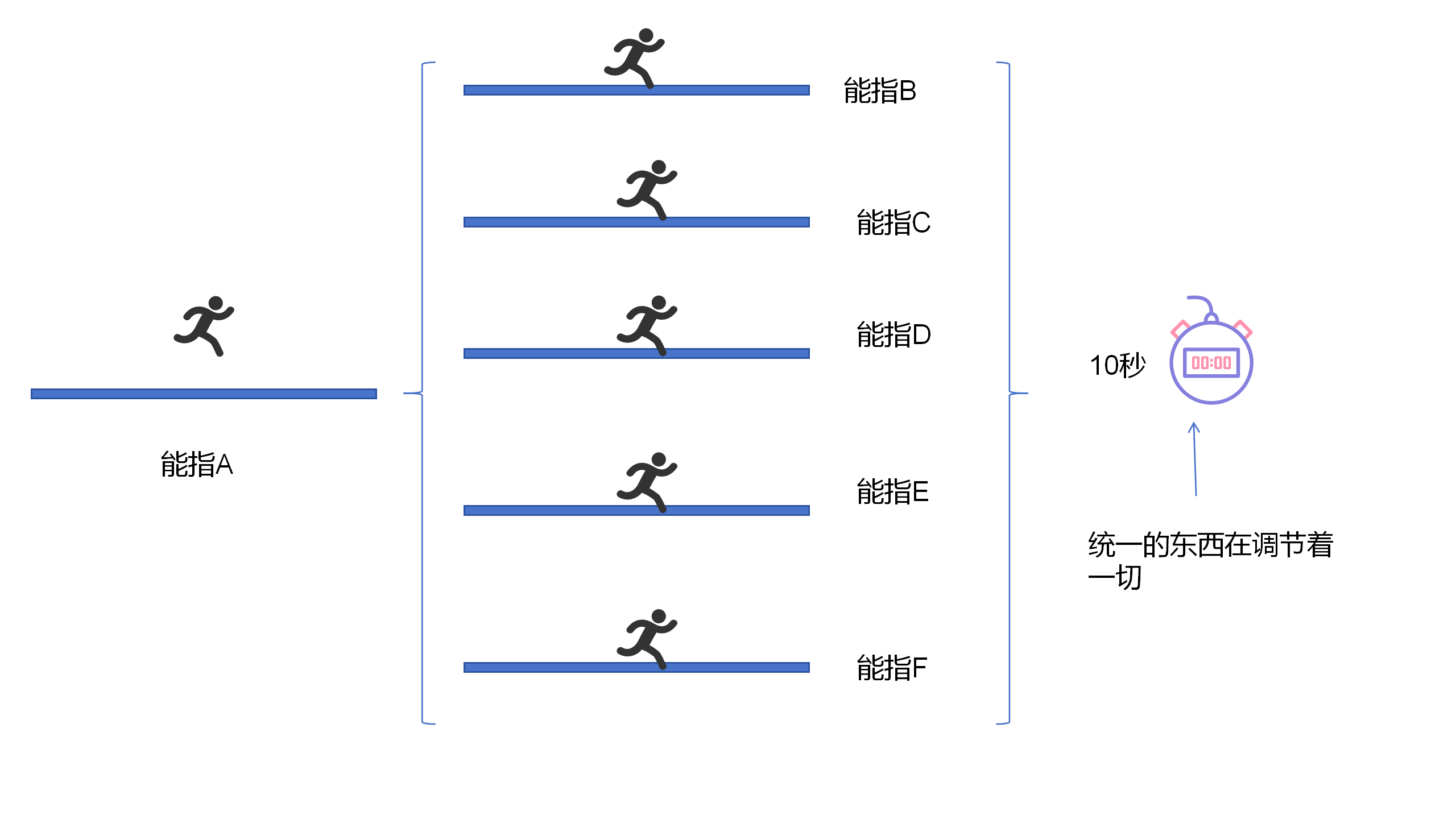
6.4特殊同義形式
每一個其他能指,都在能指A的意義關係表現中,充當同義形式,進而充當一種符碼規則。
每一個其他能指的對應關係,現在都成為一個特殊的同義形式,和其他許多特殊同義形式,並列在一起。
6.5總和、擴大的意義關係形式的缺點
①能指A的相對意義表現,是未完成的,因為它的表現系列永無止境。任何可能的自然形式,只要它和能指A表達共同的意義,那麼它就為能指A的意義關係,提供了一種新的表現材料,從而這個系列就會延長。
②這個意義關係表現的系列,是由無限多個個別表現形式所構成的,每一個個別表現都和其他所有的個別表現,完全不同,互不關聯。
③如果每一個能指的意義關係,都表現在這個擴大的形式中。那麼每一個能指的意義關係形式和符碼規則,作為一個無窮無盡的表現系列,都不同於其他每一個能指的意義關係形式和符碼規則。
6.51
擴大的形式,其缺點,反映在其中的特殊同義形式中。既然每一個能指的對應關係,在這裡都是一個特殊的同義形式,都作為一個特殊的符碼規則,與無數別的特殊同義形式和特殊符碼規則,並列在一起。所以,只存在著有侷限性的同義形式和符碼規則,其中每一個都排斥另一個。因而,從符號表意領域的整體來看,每一個特殊的同義形式和符碼規則,都是意義關係的不充分表現,都是一種不充分的符碼規則。儘管,在這些特殊形式的總和中,能指A的意義關係,獲得完全的、總和的表現形式,但是還沒有獲得統一的表現形式。

6.6
擴大的相對意義形式,只是由簡單的意義關係形式的總和,第一種形式的等式的總和,所構成的。
但是,每一個這樣的個別等式,倒裝過來,也包含著一個同一的等式:
能指B=能指A
能指C=能指A
能指D=能指A......
6.61 如果能指A與其他許多能指等同,從而把能指A的意義和意義關係,表現在一系列其他的能指上。
那麼反過來,其他許多能指,也就必然把自己與能指A等同起來,從而把它們自己的意義和意義關係,表現在同一個第三者能指A上。
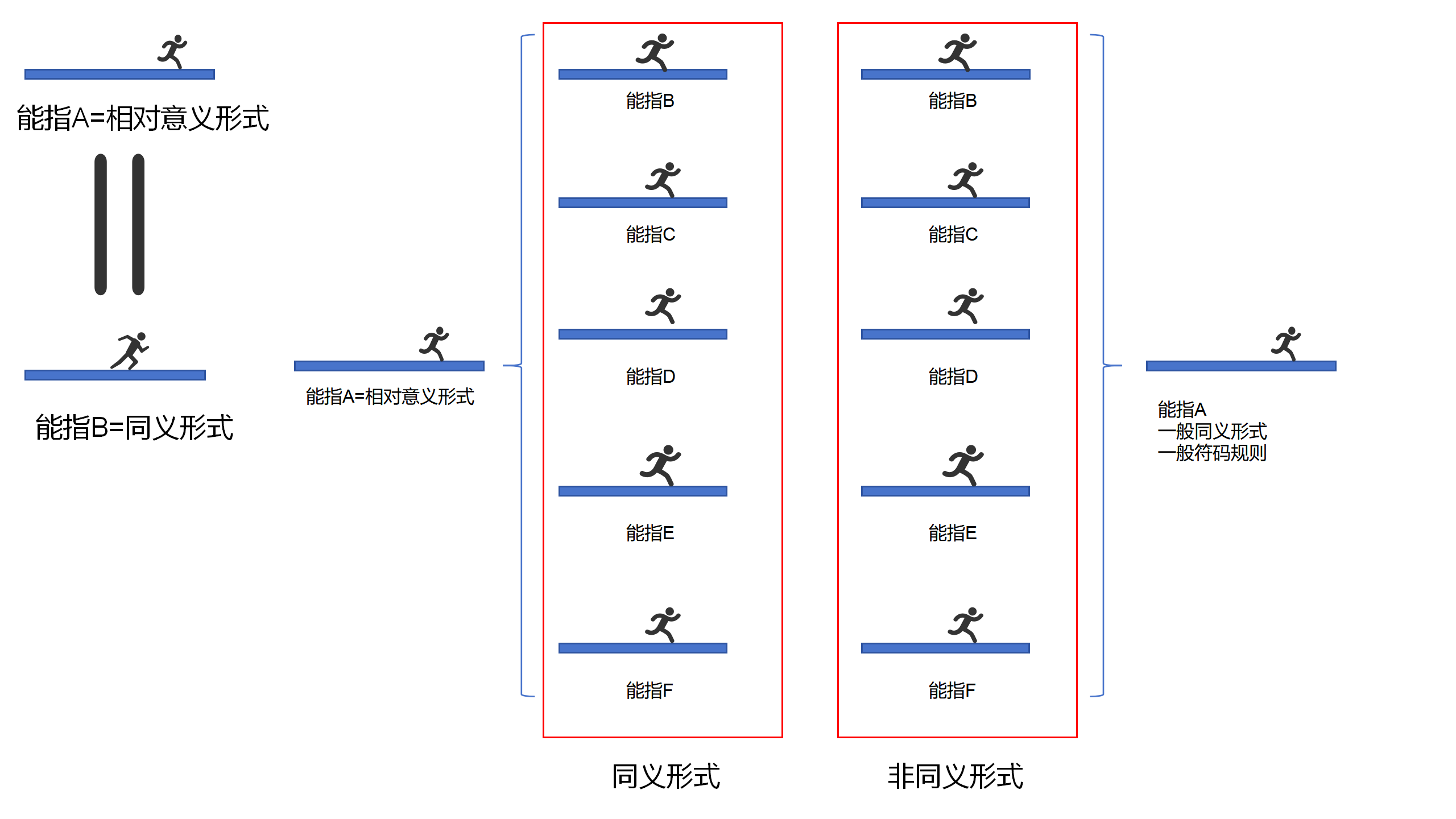
因此,把這個系列倒轉過來,也就是說,把這個系列中已經包含的相反關係,給表示出來,就會得到一般意義關係形式,也就是一般符碼規則。
七 一般符碼規則
7.1

7.2
現在,意義關係的表現
1.是簡單的,因為都是 表現在 唯一的能指上;
2.是統一的,因為都是 表現在 同一的能指上。
它們的意義關係形式,進而它們的符碼規則,是簡單的和共同的,因而是一般的。
7.3
簡單形式和總和擴大形式,都只是使一個能指的意義關係,表現在其他能指上,其他能指的自然形式與這個能指是不同的。
7.31簡單形式提供的等式是:能指A=能指B,能指C=能指D......。但是能指A和能指C,各自的意義關係表現和符碼規則,是不相同的,正如B和D不相同一樣。
7.32總和擴大形式,更完全地把一個能指的意義關係和符碼規則,給表現出來。因為它的意義關係,現在是表現在一切可能的自然形式上,並與它自身的自然形式相對立。與其他一切可能的能指相等同,只是不與自身等同。
另一方面,在這裡,能指的任何共同的意義關係表現和符碼規則,都直接被排除了,因為在每一個能指的意義關係表現中,其他一切能指,現在都只是以同義形式出現,都以符碼規則出現。
7.4
新獲得的形式,使得整個能指世界的意義關係和符碼規則,表現在同一個能指的對應關係上,這個能指是從能指世界中分離出來的。例如表現在能指A上,因而使得一切能指的意義關係和符碼規則,都通過與能指A等同,而表現出來。
每個能指的意義,作為與能指A等同的東西,不僅與它自身的自然形式相區別,而且與一切自然形式相區別。正因為這樣,才表現為它和一切能指所共有的東西。因此,只有這種形式的符碼規則,才真正使得不同的能指,作為等同的意義,而互相發生意義關係。
7.5
前兩種形式,表現一個能指的意義關係,或者是通過一個不同的能指,或者是通過許多個能指所構成的系列,這些能指均與它不同。在這兩種情況下,使自己取得一個意義關係形式,也就是它自己的符碼規則,可以說是個別能指的私事。它完成這件事,不用其他能指來幫助。對它來說,其他能指,只是起著被動的作用,作為被動的同義形式和符碼規則。
7.51 相反地,一般形式或一般符碼規則的出現,只是能指世界共同活動的結果。一個能指,之所以獲得一般的意義關係表現和符碼規則,只是因為其他一切能指,同時也用 同一個同義形式或符碼規則,來表現自身的意義關係。每一種新出現的能指,都要這樣做。這就表明,能指的意義和意義關係,只是這些能指的關係性存在。所以,它就只能通過所有能指之間全面的關係,來表現。因而它們的意義關係形式和符碼規則,必須是公認的形式。

7.6
現在,一切能指,在與能指A等同的形式上,不僅表現為 在質上等同,表現為相同的意義。而且同時,在意義的量化上,也表現為可以比較的能指量和意義量。由於它們都通過同一個能指,來反映自己的意義量化關係,這些能指量,也就相互反映和比較。例如10B=10C,10B>6D。
7.7
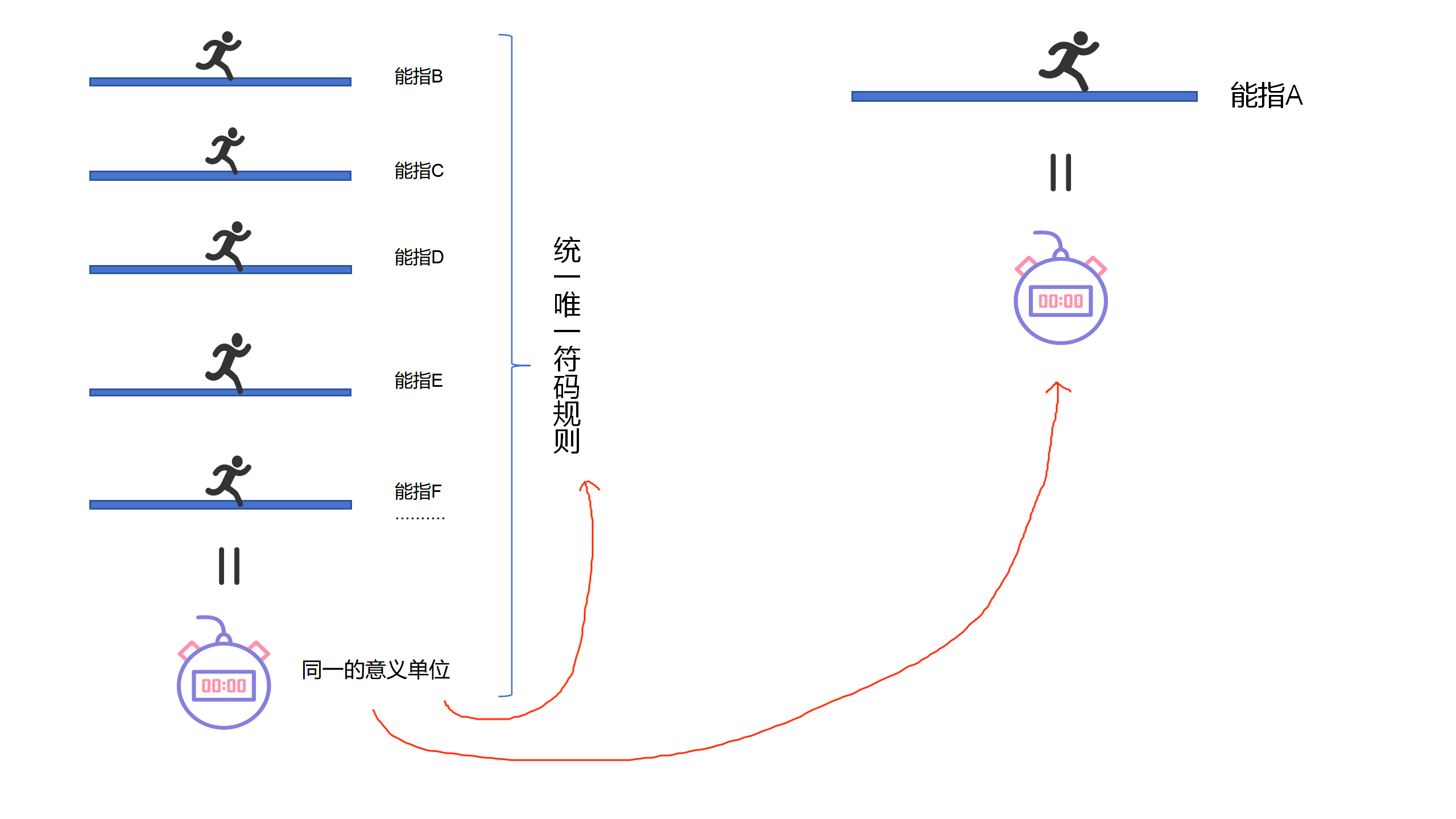
能指世界的一般意義關係形式和一般符碼規則,使得被單獨分離出能指世界的同義形式能指,獲得了一般同義形式的性質。其自身的對應關係,是這個世界的共同、統一的意義關係形式,因而也是共同、統一的符碼規則。因此,它能夠與其他一切能指直接等同,直接衡量其他能指的意義。這個單獨的能指自身的對應關係,就當作了這個統一的符碼規則,其對應的意義,就成為了統一的意義衡量單位。
這樣,這個能指的意義,也就處於一般形式,成為統一的意義單位。構成一般形式的無數等式,使得這個能指的意義,依次成為其他能指所表達的意義,從而使得這個意義,成為統一的意義單位。
八 相對形式和同義形式的發展關係
8.1
同義形式的發展程度,是同 相對形式的發展程度 相適應的。但是必須指出,同義形式的發展,只是相對形式 發展的表現和結果。
8.2
一個能指的 簡單的或個別的相對意義關係形式,使另一個能指,成為個別的同義形式和符碼規則。
擴大的相對意義關係形式,即一個能指的意義關係,在其他一切能指上的表現,賦予其他一切能指,以種種不同的特殊同義形式和特殊符碼規則。
最後,一種特殊的能指,獲得一般同義形式,是因為其他一切能指,使它成為 它們統一的、一般的意義關係形式的材料,進而成為統一的、一般的符碼規則。
8.3
意義關係形式發展到什麼程度,它的兩極,即相對意義形式和同義形式之間的對立,進而也就是相對意義和符碼規則之間的對立,也就發展到什麼程度。
8.31 第一種形式,能指A=能指B,就已經包含著這種對立,但沒有 使這種對立固定下來。從等式的左邊讀起,A是相對意義形式,B是同義形式;從等式的右邊讀起,B是相對意義形式,A是同義形式。在這裡,要把握住兩極的對立,還相當困難。
8.32 在第二種形式中,每一次,總是隻有一種能指,可以完全展開它的相對意義關係。或者說,它自身具有擴大的相對意義關係形式,這是因為,而且只是因為,其他一切能指與它相對立,處於同義形式。在這裡,不能再變換 意義關係等式的兩邊的位置,除非改變等式的全部性質,使它從總和的形式,變成一般的形式。
8.33 最後,後面一種形式,即第三種形式,給表意世界提供了一般的、統一的相對意義關係形式。是因為,而且只是因為,除了一個唯一的例外,表意世界的一切能指,都不能具有一般同義形式,都不能作為一般符碼規則。
因此,一個能指, 處於能與其他一切能指 直接等同的形式,或者說,處於統一符碼規則的形式,能夠直接衡量其他所有能指的意義關係。這是因為,而且只是因為,其他一切能指,都不是處於這種形式。
8.4
相反地,充當一般同義形式和符碼規則的能指,則不能具有表意世界的統一的、從而是一般的相對意義關係形式。
任何一個處於一般同義形式的能指,要同時具有 一般的相對意義關係形式,那麼,它必須自己給自己充當同義形式和符碼規則。於是,得到能指A=能指A,這是一個純粹的同義反復,既不表現意義關係,也不表現意義內容。
要表現一般同義能指的相對意義關係,就必須把第三種形式倒過來。一般同義能指,沒有與其他能指共同的相對意義關係形式。它的意義關係,相對地表現在其他一切能指的無限系列上。因此,擴大的相對形式,即第二種形式,現在表現為同義能指特有的相對意義關係形式。
九 一般的符碼規則→同一的意義單位
9.1
一般同義形式是意義的一種表現形式。因此,它可以屬於任何一種能指。
另一方面,一種能指處於一般同義形式(第三種形式),是因為,而且只是因為,它被其他一切能指,當作同義能指而排擠出來。這種排擠,最終限制在一種特殊的能指上。從這個時候起,表意世界的統一的相對意義關係形式,即統一的符碼規則,才獲得客觀的固定性和一般的規則效力。
9.2
同義形式,作為符碼規則,同這種特殊的能指和對應意義,規則地結合在一起。這個能指所包含的意義對應關係,就成為了表意世界的統一符碼規則,成為解釋這個世界中所有能指的意義規則,執行意義解釋的規則判定職能。
在表意世界中,即在競技活動中,起統一符碼規則的作用,進而規則判定的作用,就成為了它特有專有的職能,成為了它的獨佔權。
9.3
當然,在這裡,統一的一般規則,指的是意義,而並非能指本身。因為意義,才是能指的本體。
同義形式的關鍵,不在於能指,不在於能指自身的自然形式。這個能指可以替換為任何一個,都是無關緊要的。但是其對應的意義,必須始終都是那同一個。是這個同一的意義,決定了同義形式的存在,而不是這個能指自身是什麼樣的自然形式。
9.31 因此,真正使得這個符碼規則,成為表意世界中統一、一般的唯一符碼規則,僅僅只是這個始終同一的意義。因此,這裡的統一、一般和唯一性,僅僅只是在於這個同一的意義。僅僅只是因為對應的意義,是統一的、唯一的意義,所以,這個符碼規則才成為了統一、一般的唯一符碼規則。
9.32 因而,它所對應的意義,在整個表意世界中,就成為了同一的意義單位。即這個世界中的每一個能指單元,都必須僅僅對應於這個同一的意義。每一個能指組合即文本,所對應的意義總體,均是由這同一的意義單位所構成的。
進而,組合成文本的每一個能指單元,也就成為了同一、統一的能指單元。無論這個能指的自然形式是什麼樣子。
9.33 能指自然形式的無關性,揭示出了意義本身才是真正的一般性所在。同一的意義本身,才是這個真正的統一唯一符碼規則。
十 一定量能指→同一的意義單位
10.1
前面的論證,是以單個能指為出發條件。但是在實際的情況中,文本基本上都是由至少2個以上的能指所構成的。
就這個問題而言,儘管在實質上,單個能指和一定量的能指,沒有本質區別。但是依然可以探討一下,2個以上的一定量能指,也會推出同樣的結論嗎?即同一的意義單位。
10.2 簡單形式
隨意設置一個數量:5能指A=4能指B。
在這個等式中,5個能指A,和4個能指B,對應的意義總體,是相同的同一個意義總體。5個能指A,每一個各自所對應的意義,共同構成了一個意義總體A;4個能指B,每一個各自所對應的意義,共同構成了一個意義總體B。這兩個意義總體,是完全相同的同一個意義總體。
這也就是說,5個能指A各自所對應的意義部分,綜合起來,正好就是4個能指B各自所對應的意義部分,所綜合而成的整體。反之亦然。

10.3
在這個單獨的等式中,5個能指A與相應意義的對應關係,4個能指B與相應意義的對應關係,就構成了一個符碼規則。這個符碼規則,使得這個等式得以成立。
然而,正如前面所說的那樣,這樣的一個符碼規則,是一個個別的、特殊的符碼規則。這個符碼規則,僅僅只是針對於這個單獨的個別等式而言,才成立,它僅僅只是針對於這兩個一定量能指的個別意義關係,而存在的。
10.31 在這個符碼規則中,有不止一種可能的對應關係。因為其中的每一個能指,其對應的意義部分,具有多種的可能性。它對應的可能是這樣的,也有可能是那樣的。只要保證5個A和4個B,所構成的意義總體,恰好是相同的同一個,就可以。
這種對應關係的不唯一性,更加體現出了這個符碼規則的個別性和特殊性,更加體現出了這個符碼規則,僅僅只是針對於這一個意義關係而言的個別性存在。
10.32 因此,個別的形式,會自行過渡到更加完全的形式。
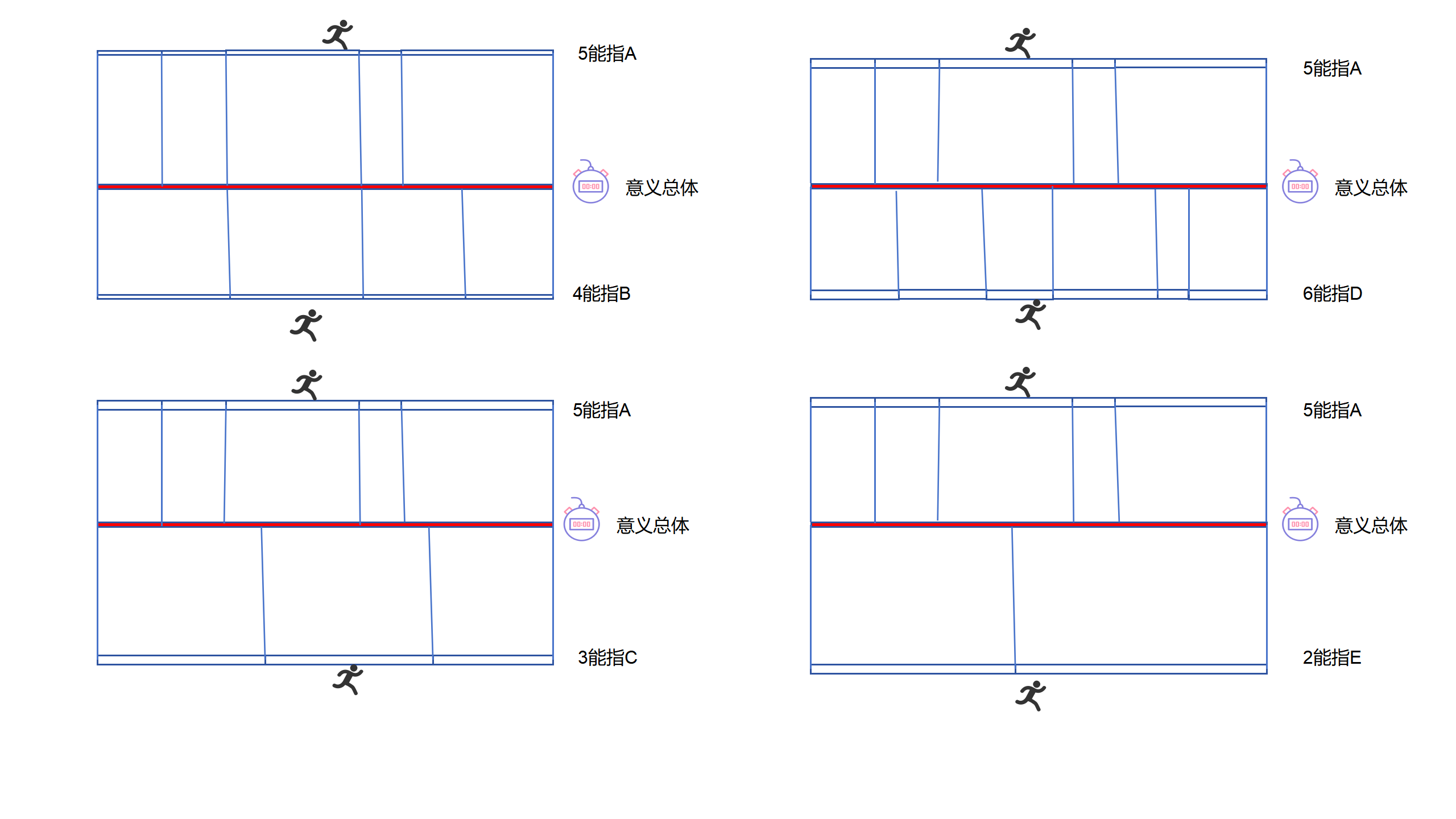
10.4 總和擴大形式
5A=4B、5A=3C、5A=6D、5A=2E........(這裡不再寫能指)
在擴大形式中,在5個能指A的每一個意義關係中,都對應一套特定的符碼規則。這套符碼規則,僅僅只是針對於這一個個別的意義關係,而存在的。
10.41 因此,如上所說
①5個能指A的符碼規則,是未完成的。因為它的表現系列永無止境。因此,符碼規則是無限多的。
②它的每一個符碼規則之間,都完全不同,且互不關聯。
③每一個一定量能指的符碼規則,即每一個文本所對應的符碼規則,都不同於其他每一個文本的符碼規則。
因此,在這種情況下,一個表意領域,將會有無數個不同的符碼規則體系。但是,這就與競技遊戲相沖突了。因為在競技活動當中,只能有一套規則體系,來進行規則判定。如果有2套以上的規則體系同時運行,那麼競技活動就無法進行了。
10.5 一般形式
同樣地,把每一個個別的等式,倒裝過來,我們就會得到一般形式,也就是一般的符碼規則。

10.51 現在,整個表意世界的符碼規則,終於獲得了唯一和統一的形式。
但是,問題在於,作為符碼規則的5個能指A,與被規則解釋的其他一定量能指,前者和後者中的每一個能指,所對應的意義,依然是不一樣的。因為這裡是一定量的能指,同一個意義總體,分別對應於不同數量的能指。
並且,如同上面所說的,在簡單形式5A=4B中,符碼規則的對應關係不具有唯一性。
因此,從單個的能指上去看,符碼規則依然是不統一的、不唯一的。
10.6
但是,在表意世界,這並不是一個問題。因為,能指並不是一種單純的自然性存在,能指並不是因為某種自然性,而成為能指。能指純粹只是一種設定,這種設定純粹是形式的和規則的。
10.61 因此,那些與5A相等同的其他一定量能指,可以在其自然形式的基礎上,重新設定能指,以使得能指的數量本身,與5A保持對齊一致。因為數量的等同,就保證了每一個能指所對應意義的同一性和唯一性,進而也就保證了符碼規則的統一和唯一。
10.62 不過,這僅僅單純只是在數量上的等同,與能指自身的自然形式無關。數量上的等同,僅僅只是為了保證整個表意世界的符碼規則,是統一和唯一的。每一個能指自身的自然形式,完全可以沒有任何相似性,只要它們所表達的意義,都是同一個。

十一 結論:同一的意義單位
11.1
經過五篇文章,幾萬字長篇累牘的論述論證,最終探索出了比賽勝負是怎麼判定出來的。
在這個過程中,這個原初的問題,經過了多重的符號學轉換,最終轉換為一個符號學問題。而在這其中,最核心的關鍵問題,就是:什麼樣的符碼規則,才能夠使得兩個不同的比賽文本,表達出一個相同的比賽結果意義?
回答這個問題的答案,實際上也就直接回答了這個最原初的問題:比賽勝負是怎麼判定出來的?
11.2
這個問題的答案,就是:同一的意義單位。
同一的意義單位,構成了一個統一和唯一的符碼規則體系。在這個符碼規則體系中,所有的能指,其對應的意義,均為相同的這同一個意義。當比賽過程結束後,競技遊戲的符碼規則,就將每個參賽者的單純比賽過程,設定為一定量的能指單元。
11.21 如果都設定為相同數量的能指單元,即每一個參賽者的一定量能指單元,其單純的量本身,被設定為相同的量。那麼所有參賽者的相同量能指單元,即每一個參賽者的比賽文本,就都表達了相同的同一個比賽結果意義,也就是比賽結果相同。
這是因為,所有比賽文本的每一個能指單元,均表達的是相同的同一個意義,也就是同一的意義單位。
11.3
因此,同一的意義單位,才是不同比賽文本,能夠表達出相同結果意義的前提條件。進而,它也就是不同比賽文本,能夠表達出不同的結果意義的前提條件。
比賽勝負是怎麼判定出來的?正是統一的符碼規則,依據這個同一的意義單位,將所有參賽者的單純比賽活動過程,設定為等量或不等量的能指單元,從而使得所有參賽者的比賽文本,表達出相同不同的比賽結果意義。這個相同不同的比賽結果,就是比賽的勝負。
最後,如果你也是對競技遊戲領域有興趣的人,那就讓我們彼此連接,共同推進這項事業的前進。感謝支持!
[未認證]競技研究社正在創作競技遊戲的理論學術研究 | 愛發電 (afdian.net)