關於獸人酒館最優解的數學計算|轉生成為魔物-3樓貓

我們來嘗試做一些定性分析，容易發現，金幣和經驗呈等比數列增加，公比q=1.05。不妨設第n級升級所需經驗 an = a0 * q^n 。那麼100級 a100 = a0 * 1.05^100。那麼從1升級到第n級所需經驗，前n項和 Sn = a0*(q^(n+1) - 1)/(q-1)，依然可近似為等比數列。即 Sn ≈ S0 * q^n

下面來計算收益：
記當前最高級為第n級，花費 x 個小時，每小時收益為 y。其中，x ∈ [1, 33.3]
即從第 (n-0.03nx) 級升到第n級，回收還要打7折，於是：
y = S0 * [ q^n * 0.7 - q^(n-0.03nx) ] / x
= S0 * q^n * [ 0.7 - q^(-0.03nx) ] / x

記 z = [ 0.7 - q^(-0.03nx) ] / x 。令 z > 0，得到 x > -ln0.7/(0.03nlnq) ≈ 244 / n
也就是說，n=100 級的時候，x需要>2.44；不到2小時就回收，此時收益是負的。而n>=244級的時候，總有z>0，收益總為正。

然後，我們來看看 z 什麼時候取到最大值。
n=100時，x=7.49時取到最大值。(而且x<=2時，z確實是負的)
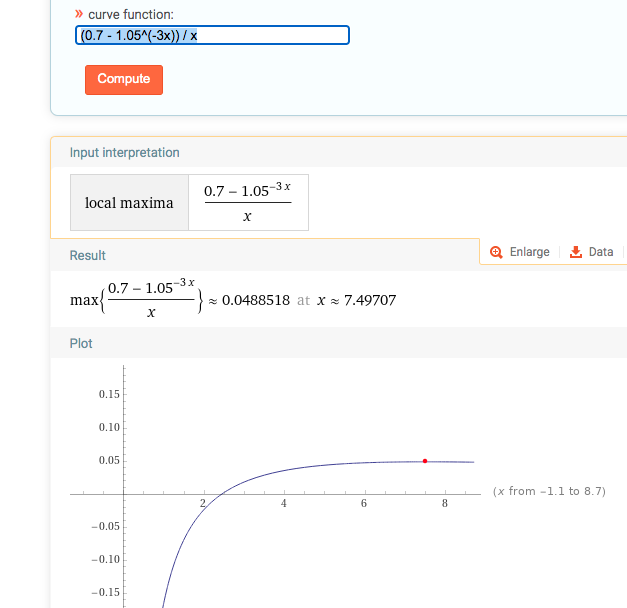
關於獸人酒館最優解的數學計算|轉生成為魔物 - 第1張

n=500時，x=1.49時取到最大值。(此時z都是正的)

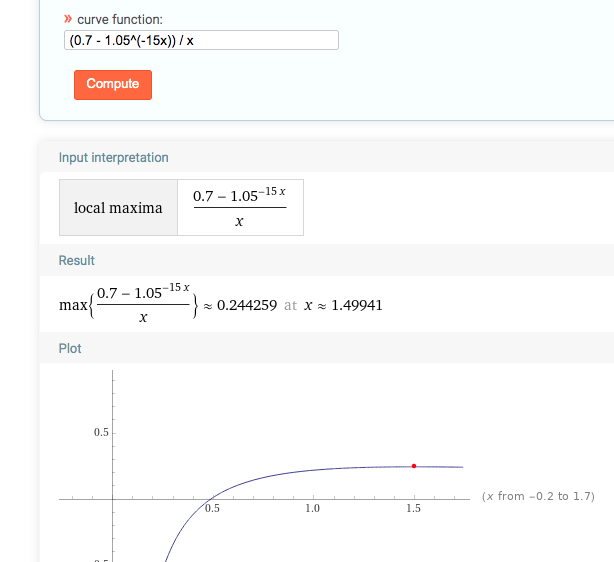關於獸人酒館最優解的數學計算|轉生成為魔物 - 第2張

n再增大，最大值點愈發靠近1小時。（也許理論上需要1小時甚至半小時收一次？）

如果後邊的公比q發生了變化，也可以用同樣的方式分析。