據我觀察，相當多的人有著這樣的認識：
傷害增加詞條比攻擊詞條高貴，因為攻擊力會被函數、協議以及自身稀釋，而傷害增加直接作用於最終傷害，不會被稀釋。（截圖僅僅作為舉例，因為有很多人都是這麼認為的，包括我，我很久以前也這麼認為）
這種看法是非常典型的半吊子理解，單論傷害增加和攻擊力，確實是傷害增加更為高貴，3.9+7.2也確實是非暴擊人形最佳的選擇。但原因絕不是因為什麼攻擊力會被稀釋，傷增作用於最終傷害。首先，不論是攻擊力還是傷增，他們都會被稀釋，因為在他們各自的乘區內都是加算，只要是加算就會被稀釋。
其次，攻擊力不會被函數協議稀釋，原因在於函數協議與攻擊力本身並不在一個乘區，都不是一起計算的數值，又談何稀釋？
最後，傷增詞條比攻擊詞條高貴純粹是因為傷增詞條難以獲得，除了套裝效果，好感加成之外，就只有A區的三個副詞條了，但是攻擊詞條除了套裝效果和好感之外，全身的算法都能洗出攻擊力，因此攻擊力幾乎必然會比傷增詞條稀釋的嚴重。很簡單的道理，我本來有1500的攻擊力又洗出一條32攻擊，和我本來有1600的攻擊力又洗出一條32攻擊這兩種情況，肯定是前一種情況的收益更大。前者收益為（1532/1500）-1=2.1%，而後者的收益為（1632/1600）-1=2%。因為多了100的基礎攻擊，所以再洗出32攻擊的收益降低了。傷增也是如此計算，只不過傷增難以獲得，很多角色默認沒有這條屬性，那麼一條3.9%傷增的收益就是3.9%，所以我們才認為傷增比攻擊收益高。概括本段，可以理解為越難堆的屬性就越高貴。
---------------------------------------------------------------------------------------
接下來，我們具體講解一下雲圖中的傷害究竟是怎麼計算的，並說明為什麼面板攻擊力不會被協議和函數稀釋。下面為傷害的計算公式，不同的乘區我用不同顏色的線標記了出來。
【各個乘區說明】
紅線部分乘區：雖然寫了很多內容，但這一部分就是點開人物面板看到的攻擊/算力的面板值，算法詞條帶來的加成都算在此處。為方便討論後文稱之為乘區A。
藍線部分乘區：這個乘區是影響攻擊/算力的協議和函數以及角色技能的專門乘區，也就是說，除了威力至上為乘算，其餘影響攻擊的函數和協議都在後方括號進行加算，其中威力至上等價於重火力，痛楚激揚等價於腦洞大開。而角色技能增幅是指類似七花光環或者芙洛倫大招所帶來的攻算加成。為方便討論後文稱之為乘區B
紫線部分乘區：這個乘區是通用傷害增加乘區，所有不帶前綴的傷害增加都在此處加算，異相和超閾的兩件套效果，副詞條中的傷增，角色好感帶來的傷增，神射帶來的傷增等都是在這裡加算。為方便討論後文稱之為乘區C。
綠線部分乘區：這個乘區計算敵方防禦和我方穿透，這一部分我以前的帖子有提到，感興趣可以移步我之前的帖子。但此貼的議題與該乘區無關，因此後文所有討論都假設我方穿透與敵方防禦相等，即該乘區數值為1。
暴擊傷害係數：如果這個傷害暴擊了，這個係數就為（1+暴擊傷害）；如果無法暴擊或者沒有暴擊，這裡就取1，本貼不討論暴擊爆傷的問題，因此後文所有的討論都默認此處為1。
特殊詞條增傷：所有帶前綴的XX增傷都在此處乘算，例如杜莎尼提供的算力傷害增加，漏洞三件套提供的負面效果傷害增加，若同時具有多個，均為直接相乘。所以這才是直接作用於最終傷害的增傷乘區，是最高貴的乘區，被削弱前的赫里斯所具有的技能增傷就是在此處計算，因此當時的先鋒服測試才將其定為頂級t0。
由公式可以看出，影響傷害的各個部分之間都是相乘，因此各個部分之間的數值相互獨立，先計算完各個乘區的數值，再將其全部相乘，即可得到最終傷害。如果裡面有一部分屬性提高了，傷害自然會增加，比如乘區A，他代表著你的面板攻算，如果這個面板攻算直接翻倍，那麼乘區A的數值也會直接翻倍，總傷害也會直接翻倍。接下來，如果進圖之後我通過協議和函數，在乘區B獲得了200%的加成，也就是乘區B的數值直接翻倍，那麼總傷害也會翻一倍。二者相乘，等於在上述情況下總傷害直接乘4。再接下來，如果我在乘區C獲得了50%的傷害增加，那麼乘區C的數值就是1.5，最後的總傷增就是4*1.5=6倍。所以才說，面板上的數值並不會被函數和協議稀釋，你每提高1%的面板攻算，都會直接乘在最終傷害上。
那什麼東西會被稀釋呢？答案是乘區內彼此加算的那些數值會相互稀釋。乘區A的例子已經在上面舉過（1500算力和1600算力分別洗出32算力的詞條，誰的實際收益高），此處省略。那乘區B就是協議和協議之間，函數和函數之間會彼此稀釋。例如你拿了痛楚激揚+30%，高騰+20%，那麼此時這個乘區的數值為1*（1+0.3+0.2）+0=1*1.5=1.5，也就是說最終傷害增加了50%。那麼這個時候，你又通過某函數獲得攻擊力+50%，你的最終傷害是直接+100%嗎？並不是如此，此時這個乘區的數值為1*（1+0.3+0.2+0.5）+0=1*2=2，那麼某函數提供的增益實際上為（2/1.5）-1=33%，也就是說數值為提高50%攻算的函數在協議的稀釋下最後實際使傷害增加了33%。乘區C與之類似，假如我好感度已經提供了5%的傷增，異相迴歸套裝又提供了5%的傷增，那麼現在就有10%的傷增，後來我又洗了一條3.9%傷增的副屬性，這條副屬性的實際收益也肯定不是3.9%，而是【（1+13.9%）/（1+10%）】-1=3.5%。
相信到這裡大家都明白了，簡而言之，乘區內部會相互稀釋，乘區和乘區之間是獨立計算的。
下面看一個反面例子：
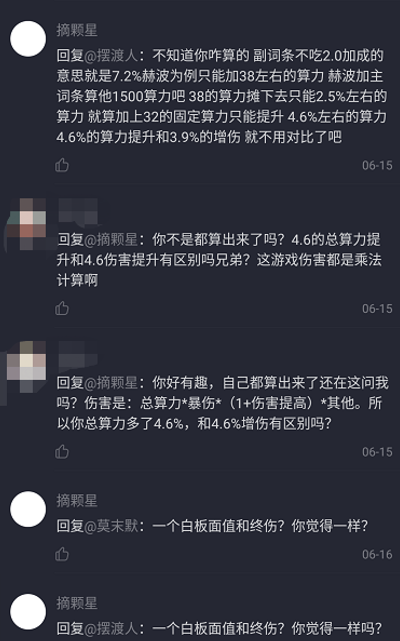
圖中此人明明已經自己估算出了兩條算力詞條的收益為4.6%（代入到上面的公式，就是乘區A的提高數值），但卻依然認為4.6%的算力不如3.9%的增傷（實際上這裡還不是3.9%，因為赫波A區的異相超閾會+5%，所以這裡的一條傷增的收益是必定小於3.9%的），很明顯就是沒有搞清楚乘區之間的關係，在眾人提醒之下仍然覺得自己沒有錯誤，然而這裡的4.6%當然比3.9%強，4.6%是乘區A的提高數值，3.9%是乘區C的提高數值，二者沒有性質上的差別，可以放在一起進行比較。和麵板數值不如終傷什麼的根本沒有關係，此人純粹就是不知道傷害計算公式，想當然的進行比較，還自以為是的說：“你覺得一樣嗎？“，屬實小丑。
---------------------------------------------------------------------------------------
為了加深理解，下面以野良為例進行相應的計算：
滿科技滿好感2.0效率的野良不穿裝備的攻擊力為507+513=1020，傷增為0。
【情景1】假設B區和C區均不穿戴任何裝備，A區單格也不裝備，只裝備一套前饋。其中前饋2為32+7.2%；前饋1有兩個選擇，一個同為32+7.2%，另一個為單條傷增3.9%。這個時候比較雙攻詞條的收益和單條傷增的收益。
首先，兩個前饋的主詞條提供了（1+48%）的攻擊力，套裝屬性又提供了（1+15%）的攻擊力，那麼此時野良的攻擊力為507+513+507*0.48+507*0.15=1020+243.36+76.05=1339.41.
再加上前饋2的兩條攻擊，則為1339.41+32+507*7.2%=1371.41+36.504=1407.914.
接下來，分別計算兩種不同的前饋1所帶來的收益。
如果是雙攻詞條，則最後的總算力為1407.914+32+36.504=1476.418
實際數據向上取整為1477.
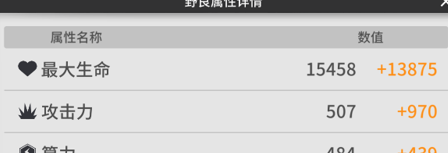那麼在乘區A內一個雙攻前饋帶來的收益則為最終攻擊除以只計算一個前饋2的攻擊再減去1，即為（1477/1408）-1=4.9%，這個結果代表的意思即雙攻詞條帶來的傷害提高為4.9%。如果是單個傷增的詞條，由於野良本身不具有任何傷增屬性，所以單個傷增所帶來的傷害提高就是3.9%，這個3.9%是在乘區C體現的。
那麼綜上所述，在其他條件不變的情況下，兩條傷增比一條傷增收益要高，雖然只有1.2%。【情景2】
剛才討論的是僅有A區算法的情況，實際肯定不是如此，因為我們的B區和C區一般也會洗出攻擊詞條，所以總的攻擊力會提高，攻擊的收益會被稀釋。現在假設我們的野良B區C區所有算法都有32攻擊，A區單格也帶主詞條6%攻擊，副詞條7.2%攻擊。
那麼繼續計算除了前饋1以外的總攻擊力，為1407.914+32*5+507*0.12+507*0.072=1407.914+160+60.84+36.504=1665.258
如果前饋1為雙攻詞條，則最後的總攻擊為1665.258+32+36.504=1733.762，那麼折算成傷害提高，就是（1733.762/1665.258）-1=4.1%
如果前饋1為單條傷增，則和情況1一致，為3.9%。可以看出，攻擊詞條越多，收益就越低，但即使是滿攻野良，雙攻的收益都比單個傷增要高。
【情況3】我們再進一步討論，假如A區使用異相兩件，單格使用6%攻擊和3.9%傷增，異相2為雙攻詞條，異相1依然在雙攻和單傷增之間進行選擇。
使用異相的話就相當於少了套裝的15%攻擊加成，多了套裝5%+單格3.9%的傷增，其餘一致。那麼除異相1副詞條以外的所有攻擊力應為1665.258-507*0.15-36.504=1552.704，傷增詞條為5%+3.9%=8.9%
如果異相1為雙攻詞條，則最後總攻擊為1552.704+32+36.504=1621.208，折算為傷害提高，就是（1621.208/1552.704）-1=4.4%
如果異相1為單個傷增詞條，則總增傷為8.9%+3.9%=12.8%，計算提高量為【（1+12.8%）/（1+8.9%）】-1=3.6%
在這種情況下，由於套裝效果和單格傷增的稀釋，導致最後一條傷增詞條的收益降低為3.6%，而雙攻詞條由於沒有前饋的套裝效果稀釋，與單格傷增的差距變的更大。
看到這裡，各位應該會自己計算某個詞條的實際收益了。當然，實際遊玩中不需要這麼麻煩，只要按照攻略給出的推薦詞條進行重構即可，因為大佬們都已經算好了最佳收益情況，不用我們自己再算一遍。如果你的數學還不錯，你還會發現，雖然各個乘區之間是獨立計算的，但彼此相乘也應該有最佳收益，例如上面的情況3中，如果使用雙攻異相，乘區A和C相乘的數值為（1+4.4%）*（1+8.9%）=1.137，即兩個乘區共同增加了13.7%的最終傷害，而情況2中完全沒有傷增詞條，堆攻擊帶來的收益是4.1%，所以二者相乘就是4.1%*1還是4.1%，這個差值還是非常大的，也就是說攻擊和傷增同時堆的效果比只有傷增或者只有攻擊都要好（其實就是求a*b最大值的問題），防禦和血量也是如此，血量和防禦都堆最後的等值血量會比只堆血和只堆防更多（我以前的帖子提到過）。
除此之外，以上討論全部基於不進圖的純面板計算，實際上當你進了圖拿了協議拿了函數，還有替補席加成，在所有情況疊加之下，不論傷增還是攻算都會被稀釋的一塌糊塗，本來這些詞條在進圖前存在微弱的差異，進圖之後這種差異會被稀釋的更低。例如射手進圖後拿了神射協議又拿了結構脆化函數，原本算法給的那點傷增就被稀釋的不成樣子了。但戰士的函數和協議裡缺少傷增，所以總體而言對戰士來說傷增詞條的含金量要比射手更高，除非你同時讓野良上場，因為野良的debuff會有15%增傷。
最後，還是那句話，這些基本問題NGA早就有大佬計算過了，結果開服快一年了還有人在爭論，還在想當然的比較，還在想當然的腦測，真是funny呢。