在我們閒來無聊刷手機時,時不時會看到這樣的新聞:

韋伯立大功

452b老素材了()

《僅》
對於這類報道,忙於和現實對線的網友們難免發出這樣的調侃:
觸不可及
為什麼我們會對這樣看似“令人興奮”的發現不屑一顧,一笑了之呢?
距離!距離是關鍵!
而事實上天文學的距離測量原理並不複雜,其中的邏輯很簡單!
標準燭光——天文學家的“量天尺”
當我們形容某件事物數量極大時,“天文數字”這個詞可是很有殺傷力的。那麼這樣大的數值,天文學家是怎麼測量出來的呢?
我們在地球上最精確的測距手段當屬雷達測距(或激光測距),然而這樣的測距方式放到宇宙尺度上可就鞭長莫及了。但這並不代表天文測距有多高深,拋開具體的技術細節不談,對於天體距離的測量,用的不是什麼高深莫測的測量方式,而是最原始、最樸素的方式:
用尺子量!

當然這可不是一般的尺子,這是一把“量天尺”。尺子上每隔一定距離會有一些“刻度”,這些刻度叫做“標準燭光”。
先別開始頭大,咱一步步來拆解:我們知道,天體的亮度(準確地說是光度)是最容易觀察到的,那麼我們可以把該發光天體放到這把宇宙巨尺上,此時天體就好像一支發著微光的蠟燭:它離我們越遠,我們所看到的燭光自然就越暗!
換言之,對於具有相同光度的一類天體,我們觀測到的光度越低,說明它離我們越遠——這就是“標準燭光”的簡單邏輯。

現在我們來選“蠟燭”:對於較近的距離,一顆恆星的光度就以夠用。而對於更遠的距離,恆星的燭光就有些暗淡了,得換“火苗”更大、更亮的蠟燭,如超新星甚至整個星系!
已經知道了用什麼樣的“蠟燭”,我們還得知道它們的燭光有多亮。我們當然不能通過瞪著清澈的大眼睛去試圖看出這些蠟燭具體有多亮,而是應該通過天體的某些物理特徵來測量。

我們把與天體的真實亮度具有相關性的物理特徵稱為“標準燭光”。
最簡單的標準燭光就是星等,星等是天文學中用來衡量天體光度的量。我們在地球上觀測到的天體亮度叫視星等;把遙遠天體挪到距離地球10pc(pc:秒差距,1pc≈3.26光年)的地方所觀測到的光度叫較絕對星等。
除了星等,可以作為標準燭光的物理特徵還有很多,如恆星的某些譜線的強度、造父變星的周光關係、球狀星團的光度函數等等。

就是這麼樸素
簡單又耐用的測距公式——距離模數
理解了什麼是標準燭光,你離測量天體距離僅差一個“神仙公式”:距離模數公式。它長這樣:
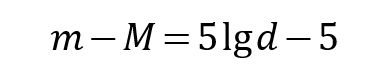
高中生都能看懂
其中m是前面所提的視星等,M是絕對星等,m減去M的差就叫做距離模數,而就d是要求的距離,是不是很簡單?
那麼為什麼說它是神仙公式呢?因為它很清晰:只需知道m與M,天體的距離就能求出,而其中的m(視星等)可以直接通過觀測得出,那麼只需知道M(絕對星等)就妥了。

你知道我想說什麼
省流:m可以直接觀測,想辦法測出M,代入公式就可以求出距離。M從何得出呢?當然就是用前面的標準燭光啦。
宇宙距離階梯——踩著星辰去往宇宙盡頭
以下是一些常用的標準燭光測距方法。這些方法技術上看似複雜,但技術背後的邏輯基本上都是圍繞求出M,或者直接求出m-M來展開的。
- 分光視差法
原理:光譜型相同的恆星的某幾條譜線強度只與絕對星等有關。
操作:用較近恆星的這幾條譜線的強度為橫座標,用經過校準的絕對星等為縱座標,得到“歸算曲線”,用它去算出待測的同光譜型恆星的絕對星等,M得出,m可直接測出,代入公式即得距離。
適用距離:30kpc
- 主星序重疊法
原理:光譜型相同的恆星具有差不多相同的絕對星等。
操作:以待測星團的視星等為縱座標,以光譜型為橫座標,得到的圖形叫赫羅圖。把待測星團的赫羅圖與已知距離的星團赫羅圖重疊,它們的區別僅僅只是縱座標不同,縱座標之差就是距離模數,代入公式可得距離。
適用距離:300kpc
- 造父變星
原理:造父變星的光度會週期性變化,描述這種光度與週期的關係叫周光關係,利用周光關係可以測得絕對星等,再觀測出其視星等,代入公式可得距離。
適用距離:30Mpc(3×10^7 pc)
此外還有很多方法,具體原理與操作就不過多介紹了,只列出其適用距離:
- 突利-費舍爾關係:100Mpc
- 法博-傑克森關係:100Mpc
- 最亮橢圓星系:1000Mpc
- Ⅰa型超新星:4000Mpc
……
可以看到這些方法所能適用的距離逐漸變遠,就好像一級一級的階梯延伸至遠處,這種象徵著距離的階梯,就叫做宇宙距離階梯。
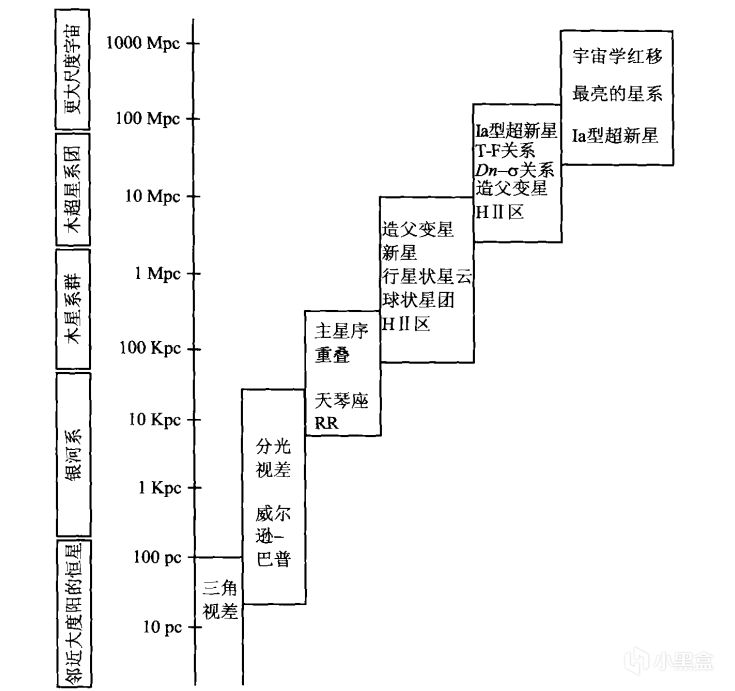
宇宙距離階梯
需要注意的是,標準燭光的適用距離越大,誤差越大,每一級階梯的標準燭光的精度都依賴於前一級階梯的校準定標。
於是,這種使用不同的標準燭光,由近到遠、逐級測距的方法稱為宇宙距離階梯。
結語
至此,一把宏大的宇宙“量天尺”就完成了!在這把尺子上,由近到遠,閃耀著不同天體的光芒。這些天體就像宇宙巨人點亮的一支支精確發光的蠟燭,它們標示的距離一級一級地延伸,最終讓我們知道:那些進入我們眼睛的星光,組成它們的光子,究竟在宇宙中跋涉了多少光年的漫漫長路……
