在我们闲来无聊刷手机时,时不时会看到这样的新闻:

韦伯立大功

452b老素材了()

《仅》
对于这类报道,忙于和现实对线的网友们难免发出这样的调侃:
触不可及
为什么我们会对这样看似“令人兴奋”的发现不屑一顾,一笑了之呢?
距离!距离是关键!
而事实上天文学的距离测量原理并不复杂,其中的逻辑很简单!
标准烛光——天文学家的“量天尺”
当我们形容某件事物数量极大时,“天文数字”这个词可是很有杀伤力的。那么这样大的数值,天文学家是怎么测量出来的呢?
我们在地球上最精确的测距手段当属雷达测距(或激光测距),然而这样的测距方式放到宇宙尺度上可就鞭长莫及了。但这并不代表天文测距有多高深,抛开具体的技术细节不谈,对于天体距离的测量,用的不是什么高深莫测的测量方式,而是最原始、最朴素的方式:
用尺子量!

当然这可不是一般的尺子,这是一把“量天尺”。尺子上每隔一定距离会有一些“刻度”,这些刻度叫做“标准烛光”。
先别开始头大,咱一步步来拆解:我们知道,天体的亮度(准确地说是光度)是最容易观察到的,那么我们可以把该发光天体放到这把宇宙巨尺上,此时天体就好像一支发着微光的蜡烛:它离我们越远,我们所看到的烛光自然就越暗!
换言之,对于具有相同光度的一类天体,我们观测到的光度越低,说明它离我们越远——这就是“标准烛光”的简单逻辑。

现在我们来选“蜡烛”:对于较近的距离,一颗恒星的光度就以够用。而对于更远的距离,恒星的烛光就有些暗淡了,得换“火苗”更大、更亮的蜡烛,如超新星甚至整个星系!
已经知道了用什么样的“蜡烛”,我们还得知道它们的烛光有多亮。我们当然不能通过瞪着清澈的大眼睛去试图看出这些蜡烛具体有多亮,而是应该通过天体的某些物理特征来测量。

我们把与天体的真实亮度具有相关性的物理特征称为“标准烛光”。
最简单的标准烛光就是星等,星等是天文学中用来衡量天体光度的量。我们在地球上观测到的天体亮度叫视星等;把遥远天体挪到距离地球10pc(pc:秒差距,1pc≈3.26光年)的地方所观测到的光度叫较绝对星等。
除了星等,可以作为标准烛光的物理特征还有很多,如恒星的某些谱线的强度、造父变星的周光关系、球状星团的光度函数等等。

就是这么朴素
简单又耐用的测距公式——距离模数
理解了什么是标准烛光,你离测量天体距离仅差一个“神仙公式”:距离模数公式。它长这样:
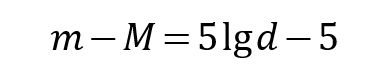
高中生都能看懂
其中m是前面所提的视星等,M是绝对星等,m减去M的差就叫做距离模数,而就d是要求的距离,是不是很简单?
那么为什么说它是神仙公式呢?因为它很清晰:只需知道m与M,天体的距离就能求出,而其中的m(视星等)可以直接通过观测得出,那么只需知道M(绝对星等)就妥了。

你知道我想说什么
省流:m可以直接观测,想办法测出M,代入公式就可以求出距离。M从何得出呢?当然就是用前面的标准烛光啦。
宇宙距离阶梯——踩着星辰去往宇宙尽头
以下是一些常用的标准烛光测距方法。这些方法技术上看似复杂,但技术背后的逻辑基本上都是围绕求出M,或者直接求出m-M来展开的。
- 分光视差法
原理:光谱型相同的恒星的某几条谱线强度只与绝对星等有关。
操作:用较近恒星的这几条谱线的强度为横坐标,用经过校准的绝对星等为纵坐标,得到“归算曲线”,用它去算出待测的同光谱型恒星的绝对星等,M得出,m可直接测出,代入公式即得距离。
适用距离:30kpc
- 主星序重叠法
原理:光谱型相同的恒星具有差不多相同的绝对星等。
操作:以待测星团的视星等为纵坐标,以光谱型为横坐标,得到的图形叫赫罗图。把待测星团的赫罗图与已知距离的星团赫罗图重叠,它们的区别仅仅只是纵坐标不同,纵坐标之差就是距离模数,代入公式可得距离。
适用距离:300kpc
- 造父变星
原理:造父变星的光度会周期性变化,描述这种光度与周期的关系叫周光关系,利用周光关系可以测得绝对星等,再观测出其视星等,代入公式可得距离。
适用距离:30Mpc(3×10^7 pc)
此外还有很多方法,具体原理与操作就不过多介绍了,只列出其适用距离:
- 突利-费舍尔关系:100Mpc
- 法博-杰克森关系:100Mpc
- 最亮椭圆星系:1000Mpc
- Ⅰa型超新星:4000Mpc
……
可以看到这些方法所能适用的距离逐渐变远,就好像一级一级的阶梯延伸至远处,这种象征着距离的阶梯,就叫做宇宙距离阶梯。
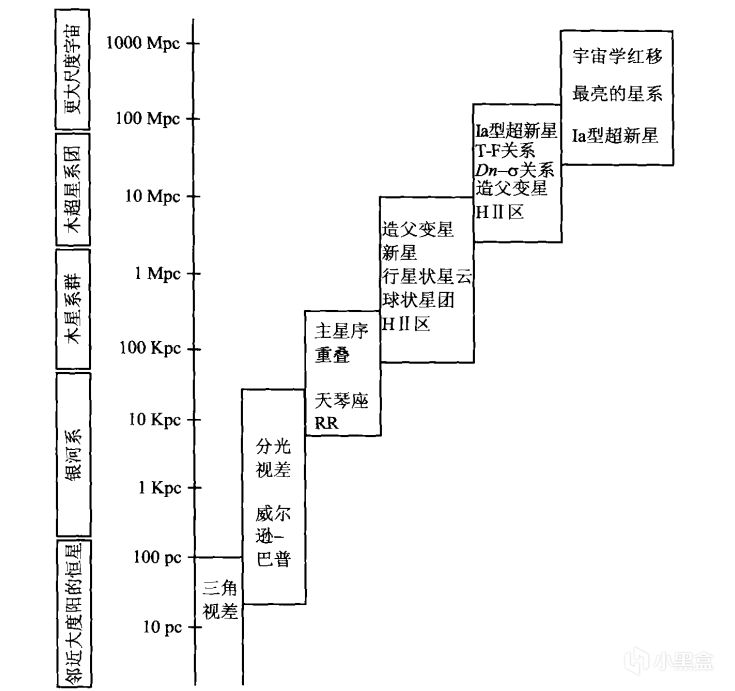
宇宙距离阶梯
需要注意的是,标准烛光的适用距离越大,误差越大,每一级阶梯的标准烛光的精度都依赖于前一级阶梯的校准定标。
于是,这种使用不同的标准烛光,由近到远、逐级测距的方法称为宇宙距离阶梯。
结语
至此,一把宏大的宇宙“量天尺”就完成了!在这把尺子上,由近到远,闪耀着不同天体的光芒。这些天体就像宇宙巨人点亮的一支支精确发光的蜡烛,它们标示的距离一级一级地延伸,最终让我们知道:那些进入我们眼睛的星光,组成它们的光子,究竟在宇宙中跋涉了多少光年的漫漫长路……
