原文鏈接：點擊跳轉
作者：Sébastien Bénard
譯者：mnikn

1. 什麼是 Bresenham 直線算法

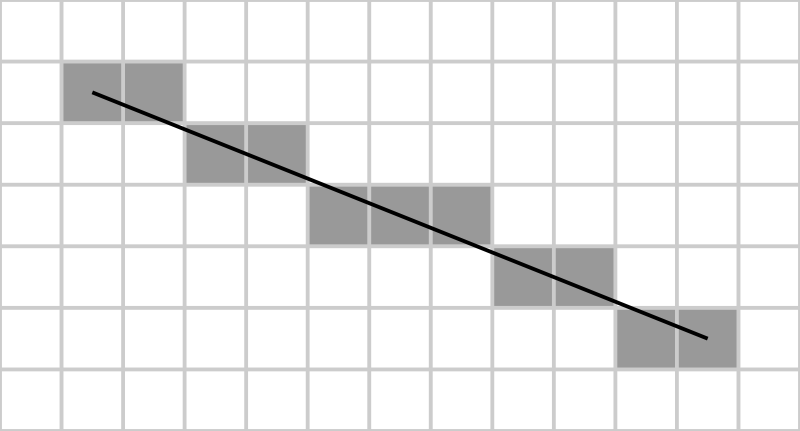
Bresenham 直線算法是個很通用的算法，幾個月前我才剛剛瞭解到它，它在許多用途上都很實用。這個算法基本用來在兩點之間基於網格（例如像素網格）繪製一條直線，繪製出來的直線是 pixel perfect 的，看起來很酷（譯註：pixel perfect 的定義參考這篇文章中有關線條的說法，幸好學過像素畫不然還不知道這個是什麼）。

不過這個算法還有很多有趣的用途：

視線檢測
尋路算法優化
平滑尋路路徑
視野檢測（圓錐）
光照
...

2. 實現

你可以看下基於 Haxe 的實現，這部分代碼在我的 GitHub 倉庫裡面：BRESENHAM.HX

以下是基於 Haxe 的實現：

function getLine(x0:Int, y0:Int, x1:Int, y1:Int) : Array<{x:Int, y:Int}> {
    var pts = [];
    var swapXY = fastAbs( y1 - y0 ) > fastAbs( x1 - x0 );
    var tmp : Int;
    if ( swapXY ) {
        // 交換 x 和 y
        tmp = x0; x0 = y0; y0 = tmp; // 交換 x0 和 y0
        tmp = x1; x1 = y1; y1 = tmp; // 交換 x1 和 y1
    }

    if ( x0 > x1 ) {
        // 確保 x0 < x1
        tmp = x0; x0 = x1; x1 = tmp; // 交換 x0 和 x1
        tmp = y0; y0 = y1; y1 = tmp; // 交換 y0 和 y1
    }

    var deltax = x1 - x0;
    var deltay = fastFloor( fastAbs( y1 - y0 ) );
    var error = fastFloor( deltax / 2 );
    var y = y0;
    var ystep = if ( y0 < y1 ) 1 else -1;
    if( swapXY )
        // Y / X
        for ( x in x0 ... x1+1 ) {
            pts.push({x:y, y:x});
            error -= deltay;
            if ( error < 0 ) {
                y = y + ystep;
                error = error + deltax;
            }
        }
    else
        // X / Y
        for ( x in x0 ... x1+1 ) {
            pts.push({x:x, y:y});
            error -= deltay;
            if ( error < 0 ) {
                y = y + ystep;
                error = error + deltax;
            }
        }
    return pts;
}

注意 fastAbs 和 fastFloor都是 absolute 和 floor 的極致性能實現版：

static inline function fastAbs(v:Int) : Int {
    return (v ^ (v >> 31)) - (v >> 31);
}

static inline function fastFloor(v:Float) : Int {
    return Std.int(v); // 實際上更多時候是在去除後面的小數值而不是向零取捨
}

對於 Bresenham 算法，你需要了解的是:

它很容易實現，而且很高效。
為了性能，我把 if( swapXY ) 移到了循環外面（只有當調用次數很多的時候才需要這麼做）。
數組的內存分配（例如 var pts = []）是有性能損耗的。出於性能考慮你可能想要特殊處理下這個函數，不讓這個函數每次執行都新建一個數組存點。
數組裡點的順序可能會變化。這點非常重要！這意味著數組可能返回 x0,y0 到 x1,y1的點或者剛好相反，這取決於直線的角度。

我建議你讀下 Wikipedia 上有關 Bresenham 直線算法的常規實現，尤其是如果你想要根據情況對它做一些特殊處理，在上面你還能發現一些有趣的優化技巧。

所以這個算法我們要怎麼去用呢？

3. 使用案例

3.1. AI

當你想要寫一個怪物敵人的 AI 時，你通常會遇到兩個很基礎的問題：

怪物和玩家接近嗎（基礎的做法是檢查之間的距離）
怪物能夠看到玩家嗎

第二個問題可以用 Bresenham 直線算法來輕鬆解答，只需要用它來檢測怪物的視線和玩家中是否有障礙物就好。

function checkLine(x0:Int, y0:Int, x1:Int, y1:Int, rayCanPass:Int->Int->Bool) {
    var swapXY = fastAbs( y1 - y0 ) > fastAbs( x1 - x0 );
    var tmp : Int;
    if ( swapXY ) {
        // swap x and y
        tmp = x0; x0 = y0; y0 = tmp; // swap x0 and y0
        tmp = x1; x1 = y1; y1 = tmp; // swap x1 and y1
    }

    if ( x0 > x1 ) {
        // make sure x0 < x1
        tmp = x0; x0 = x1; x1 = tmp; // swap x0 and x1
        tmp = y0; y0 = y1; y1 = tmp; // swap y0 and y1
    }

    var deltax = x1 - x0;
    var deltay = fastFloor( fastAbs( y1 - y0 ) );
    var error = fastFloor( deltax / 2 );
    var y = y0;
    var ystep = if ( y0 < y1 ) 1 else -1;

    if( swapXY )
        // Y / X
        for ( x in x0 ... x1+1 ) {
            if( !rayCanPass(y,x) )
            return false;

            error -= deltay;
            if ( error < 0 ) {
                y = y + ystep;
                error = error + deltax;
            }
        }
    else
        // X / Y
        for ( x in x0 ... x1+1 ) {
            if( !rayCanPass(x,y) )
            return false;

            error -= deltay;
            if ( error < 0 ) {
                y = y + ystep;
                error = error + deltax;
            }
        }
    return true;
}

這個版本沒有返回任何位置點，它只是對於線上的每個點都調用下函數（rayCanPass），如果函數返回為 false，那麼整個 checkLine 就停止運行然後返回 false。

例如:

checkLine(
    mob.x, mob.y, 
    player.x, player.y,
    function(x,y) return collisionMap[x][y] == false
);

這樣的實現很簡潔而且高效，尤其是當發現障礙就停止循環。注意如果你讓 checkLine 函數循環太多次的話，Flash 上的性能可能不會太好，因為 Flash 函數調用性能損耗挺高。（譯註：這篇文章發佈在 2013 年，現在 Flash 都已經進入墳墓了……）

3.2. 尋路算法優化

當你在寫尋路算法的時候（例如 A-star 算法），現實會讓你發現調用這些算法在實時遊戲中會消耗不少性能。所以你要儘可能不去調用尋路算法。

根據我們上述的例子，如果你能夠回答“怪物能夠看到玩家嗎”這個問題，你就可以利用這種方式來減少不必要的尋路算法調用。

3.3. 平滑尋路路徑

大部分的尋路算法會返回從起點到終點間的所有的位置點，不過對於網格來說會有點生硬。

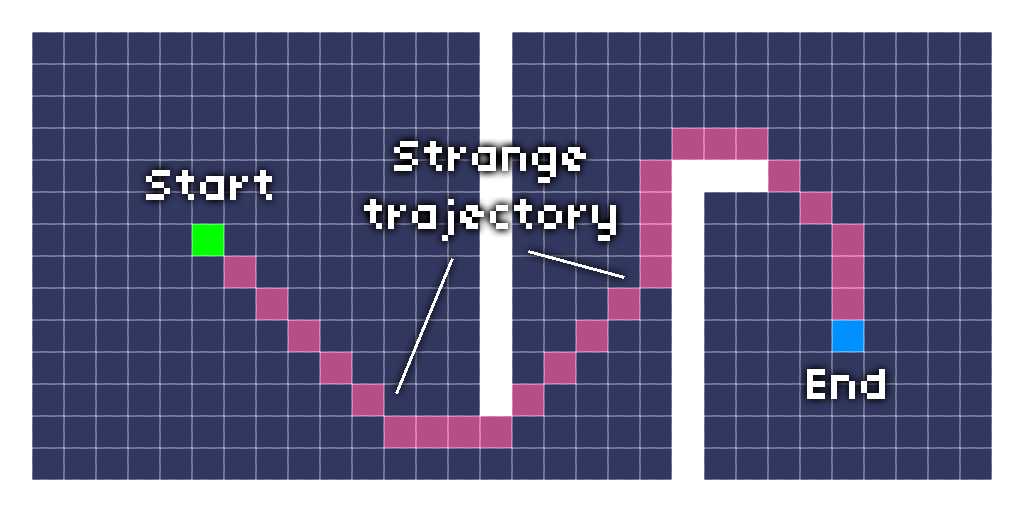
Bresenham 直線算法可以很輕鬆就讓尋路算法的結果更加“平滑”一些，你需要做的是：

設置一個叫 REF 點，這個點等於起點
檢測 REF 點能否在路徑上“看見”第三個點，如果可以的話，把第二個點去掉，因為這個點沒用
重複檢測操作，如 REF 點能否看到第四個點，以此類推
如果 REF 點不能看到我們給過去的點，那麼上一個點就有用了，我們保留它。在這種情況下，REF 點就變成了上一個點，然後對於剩下的點，重複剛才的算法
最後，通過只保留能夠相互看見的有用點，你就可以讓路徑更加簡潔

3.4. 視野檢測（圓錐）

想要實現像 Metal Gear Solid

or Commando 那樣的圓錐視野不難。

檢測敵人是否看到玩家的做法：

檢查下兩者間的距離
如果在範圍內，計算敵人和玩家之間的角度（Math.atan2）
如果計算出來的角度和敵人的方向角度之間的角距離小於圓錐範圍 / 2，開始 Bresenham 直線算法檢測
如果玩家沒有躲著什麼障礙物後面...警報響起來吧！

3.5. 關於對角的注意點

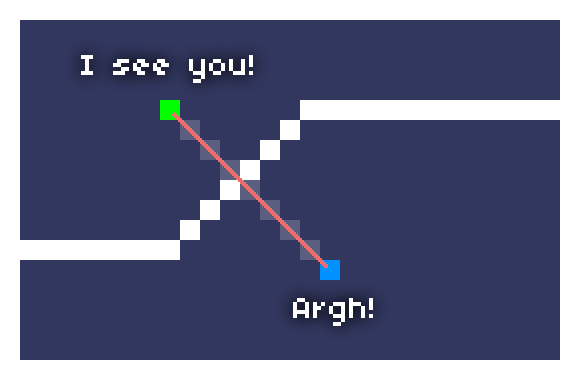
注意如果你的遊戲中有對角的牆，基礎的 bresenham 直線算法還是能夠穿牆而望的。

3.6. 光照

如果你需要遍歷範圍內的所有點，例如 rouge-like 遊戲裡面的火炬，你可以使用 Bresenham 直線算法來檢測火炬是否能夠看到某個特定點。如果可以，那你就可以點亮那個單元格，然後光照的亮度等於單元格距離火炬的距離 / 最大光照距離。

var intensity = 1 - dist / maxDist; // 0=沒有光照, 1=全光照

這樣一個算法實時運行的話會相當耗性能，因為你需要遍歷每個點和火炬來計算光照值。不過如果你不需要很實時，例如火炬不需要動態移動，你可以在遊戲開始前預計算你的光照值，這樣消耗基本上就忽略不計了，而且這實現起來一點都不難。

for (dx in -radius...radius+1)
    for(dy in -radius...radius+1) {
        var x = source.x + dx;
        var y = source.y + dy;

        var d = distance(source.x, source.y, x, y);
        if( d<=radius && checkLine(source.x,source.y, x,y, hasNoCollision) ){
            var intensity = 1 - d/radius;
            // 更新光照值，繪製，...
        }
    }

對於玩家你還是可以擁有動態光照的，像 roguelike 遊戲，只有在玩家的單元格發生變化時才重新計算光照（例如移動）。這裡面還有很多優化的空間，不過具體如何實現取決於你的需求。

3.7. Pixel perfect 的圓

Bresenham 直線算法通常用作畫直線，不過其實也可以用來畫圓。實際上實現這一點的作者並不是 Bresenham 本人，不過這個實現方法深受 Bresenham 的啟發。

它不像直線那麼常用，但是在一些情況下還是有作用的，而且很容易實現。更多的細節可以在 Wikipedia “Midpoint circle algorithm” 詞條頁面上看到。

在檢測中通過添加一些額外的點來修正圓：你可以修正圓裡面的中斷的地方（例如 error < 0），檢測中斷周圍的其它點。效果是在不影響水平線和垂直線的情況下，讓對角線變得更粗。（譯註：這段作者說得有點雲裡霧裡，簡單來說就是讓一個不 pixel perfect 的圓通過修正變得 pixel perfect）

譯者的話

現在大部分遊戲引擎都內置了尋路算法、動態光照等，可能大多數情況下使用內置的算法就能解決問題，不過文章中的思路還是很值得借鑑的，尤其是當發現內置的算法不滿足需求時。