本教学面向刚入坑的小萌新(虽然我也是),但希望我的计算能给大家带来一些启发,欢迎各位斧正。
场景一
不妨假设这样一个场景:战士每回合的能量是3点,牌组中有x张牌,其中
想要计算这些数值,我们首先要计算这些数据:
- 一次牌组循环所经历的平均回合数:x/5
- 一次牌组循环所产生的总能量:3x/5
- 打出所有打击所需要的能量:x/2
了解了这些,我们可以看出,在一次牌组循环中,产生的能量是大于打出所有打击所需要的能量的,所以我们不需要考虑因为能量不足导致无法达到理论最大伤害的情况出现。
那么在一次牌组循环中,理论最大伤害为x/2 * 6 = 3x,每回合平均最大伤害为3x / (x/5) = 15。
场景二
现在我们多出了一些变化,假设在刚才的牌组中加入一张剑柄打击,情况又会如何呢?笔者接下来带领大家重新计算一下数值。现在牌组中有x+1张牌了,其中:
- 一次牌组循环所经历的平均回合数:(x+1-1)/5(这里-1是因为剑柄打击能帮助我们抽一张牌)
- 一次牌组循环所产生的总能量:3(x+1-1)/5
- 打出所有打击和剑柄打击所需要的能量:x/2+1
情况似乎有所变化,我们发现打出所有打击和剑柄所需要的能量有可能会大于一次牌组循环所产生的总能量,此时我们就需要分类讨论:
- 当牌组循环的产能大于所需能量时,即3(x+1-1)/5 > x/2 + 1:此时x>= 10,理论最大伤害为3x + 9,平均每回合最大伤害为(3x + 9)/((x+1-1)/5)=15(x+3)/x=15+45/x。又因为x>= 10,所以当x= 10的时候,平均每回合输出的伤害最高,并且这个数值会随着x的增大而被稀释(即减小)。
- 当牌组循环的产能小于所需能量时,此时x< 10且x>= 5(确保每回合都可以抽到至少5张牌):那么此时理论最大伤害即为打出一张剑柄打击后,剩余所有能量都用来打出打击。计算值为:9+(3x/5-1)*6 = 3+18x/5。平均每回合最大伤害为:(3+18x/5)/((x+1-1)/5)=18+15/x。同样的,这个数值会随着x的增大而减小。
那么在场景2中,我们就可以尝试绘制下面这张图像了:
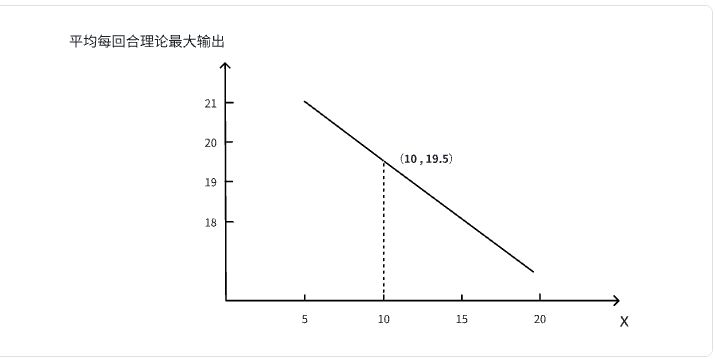
当然,上面出现的都是理想情况下的极限输出(一回合抽上手5张防的情况倒也并不多见),并且笔者没有考虑防御的情况,请勿见怪,举这两个例子是为了帮助读者更好地理解牌组循环的重要性。
简单总结
通过上面两个例子,相信读者已经注意到了,在我们的模拟过程中,有两个非常重要的概念在频繁出现,其中一个就是牌组循环,另一个则是隐性的效费比。效费比的定义为每1点能量所能产出的伤害数值。
当我们计算每回合最大平均伤害时,我们实际在计算的事实上是一次牌组循环的理论最大伤害/一次牌组循环所经历的回合数。而牌组循环的越快,其一次循环所经历的回合数就越小;每张输出牌的效费比越高,一次循环中理论最大伤害也就越高。这两者共同决定了每回合最大的平均伤害的数值。
如此看来,剑柄打击这张牌强势的原因则不言而喻了:效费比高的同时,能抽一张牌,加快牌组循环速度,从而大大提高每回合平均最大伤害。其他的卡牌也同理。