這篇內容本來是我分享在博客園上的技術博客,考慮到這些資料可能會對小黑盒平臺上的遊戲玩家們有幫助,這裡決定抄送一份在小黑盒發佈。
本文作者:多玩我的世界盒子
本文鏈接:https://www.cnblogs.com/BOXonline1396529/articles/18208092
版權聲明:本作品採用知識共享署名-非商業性使用-禁止演繹 2.5 中國大陸許可協議進行許可。
2024 年 5 月我的實驗課作業要求使用遺傳算法解決任意的交通領域實踐問題。我用 MATLAB 自己寫了一個遺傳算法求解器,對 CVRP 問題進行了求解,這裡把代碼分享給大家。
CVRP 問題,即包含容量限制的車輛路徑優化問題(Capacity Vehicle Routing Problem),是物流和運輸領域中的一個經典優化問題。其目標是確定一組車輛從一個配送中心出發,訪問一系列客戶節點並返回配送中心的 最優路徑方案。該問題的目的是在滿足所有客戶需求和車輛運載能力限制的同時,最小化總行駛距離或總成本。該問題可以被認為是 TSP 問題的一種變體,即增加了車輛容量限制的 TSP 問題。TSP 問題也可以被理解為無容量限制的 VRP 問題,即一輛車走完全局最短路即可滿足所有節點的需求。
我在寫這個求解器的時候我儘量去做了很多的適配,比如讓這個求解器能夠適配儘可能多的 CVRP 問題,以及讓代碼註釋儘可能詳細,以便大家能夠在我寫的代碼基礎上自行開展學習等等。原本就想著等我把這個作業寫完之後就把內容發到博客裡面來的,但寫完之後發現代碼文件太多太長了,沒有辦法直接插入到博客裡面來。博客園沒有云存儲,CSDN 又要充米恰金豆,所以只好上傳到 Gitee 平臺上了,項目地址是這個 通過遺傳算法實現車輛路徑優化問題求解:https://gitee.com/boxonline_1396529/ga-cvrp-opt
如果您還不知道如何從 Gitee 上面下載代碼,請查看這篇文章:沒有git,如何下載gitee代碼?
https://www.cnblogs.com/boxonline1396529/p/18207930
示例代碼及算例
算例生成
算例來自於 MATLAB 官網文章 CapacitatedVehicle Routing Problem(https://www.mathworks.com/help/matlab/math/quantum-capacitated-vehicle-routing.html),座標點及各個顧客的需求量根據原文中的方法隨機生成。算例可視化如下圖所示,詳情請參照原文。
Capacitated vehiclerouting is a combination of a knapsack problem and a traveling salespersonproblem. The problem is for a vehicle (or set of vehicles) to visit a group ofcustomers that are geographically distributed. The vehicle has a capacityconstraint, where the capacity refers to a quantity that the vehicle deliversto each customer. The problem has a central depot, and the vehicle must return tothe depot after each visit to a set of customers, or route. The problem is tovisit the customers at minimal cost, where the cost is the total length of theroute for visiting a group of customers.
The followingfigure shows four routes originating from a single point, the depot. Theseroutes do not represent a minimal solution, because nodes 2 and 3 (at least)should be visited in the opposite order. The route containing nodes 2 and 3 hasa self-intersection, which does not occur in an optimal tour.
下面的代碼可以生成算例:
% CapacitatedVehicle Routing Problem
rng(1) %For reproducibility
numCustomers = 24; %Depot at [0 0] makes 25 locations
depot = [0 0]; %Depot at the origin
loc = [depot; randi([-50, 50],numCustomers,2)];
% Integers from -50 to 50, 24-by-2
demands = 100*randi([1, 25],numCustomers,1);
capacity = 6000;
算例可視化
同樣是官網提供的代碼,用下面的代碼可以對算例進行可視化:
% Plot thelocations with demands overlaid
% figure;
scatter(loc(:,1),loc(:,2),'filled','SizeData',25);
text(loc(:,1),loc(:,2),["Depot"; num2str((1:numCustomers)')]);
title("Customer Locations and Demands");
hold off;
如下圖所示:

算例可視化
算法使用顧客與倉庫之間的 OD 矩陣,而不是真實座標進行運算,保障了算法的兼容性和可拓展性。
取得 OD 矩陣,可以使用如下的代碼:
% 生成 OD 矩陣
% OD_mat = squareform(pdist(loc));
% 鑑於一些人的電腦裡可能沒有統計與機器學習工具箱,pdist 函數有可能無法使用
% 下面的代碼也可以獲取原問題的 OD 矩陣
OD_mat = zeros(numCustomers, numCustomers);
for i = 1:numCustomers+1
for j = 1:numCustomers+1
OD_mat(i, j)= sqrt(sum((loc(i, :)- loc(j, :)).^2));
end
end
算法設計簡述
基因編碼設計: 基因編碼設計參考了博客:用遺傳算法解決VRP問題(https://blog.csdn.net/panbaoran913/article/details/128250015),其基本邏輯為:首先隨機生成所有顧客節點編號的隨機排列,再在其中插入數量相當於運載工具數量減去1 數量的0,即,設此時共有 輛車,則插入的 0 元素數量為 。每一段用0 分割的節點序列即代表一輛車的訪問節點次序。
如:設此時存在基因編碼方案 23 9 0 7 6 4 0 1 8 5,代表第一輛車訪問節點的順序是2、3、9,第二輛車訪問的節點是 7、6、4,第三輛車訪問的節點是 1、8、5。詳情參見原文所述。
約束處理: 算法強調並實現瞭如下的模型約束:
• 每個客戶節點必須被訪問一次。
• 每輛車從配送中心出發並返回配送中心。
• 每輛車的總負載不能超過其最大載重量。
適應度函數取值: 取總路程倒數為適應度函數值。對於超出模型約束(車輛數量約束和總載重量限制約束)的個體,強制令其適應度函數值為0。
交叉和變異方法: 使用單點交叉和單點變異的方法。對於交叉、變異後產生不符合模型約束的非法個體的情形,不予交叉變異。 該策略通過在交叉、變異前提前對交叉編譯產生的個體進行檢驗並根據檢驗結果進行判斷來實現。
精英策略: 算法保存歷次迭代中取得的最優適應度個體,並在未來次數迭代中使用該個體替換種群中適應度最低的個體,避免種群劣化。
對於代碼裡的詳細的信息內容,請自行下載代碼查看。
算法迭代過程
設置迭代次數為 1000 次,種群大小為 50000。由於交叉變異過程受到模型約束的限制,為了保障實際的交叉變異發生率,應當適當增加交叉變異概率。這裡取得交叉變異概率分別為 Pc = 0.9,Pm = 0.09。
求解器的使用是很容易的。使用 help GA_CVRP_optimize 命令可以查看求解器的使用方法。這些代碼註釋我已經寫得非常詳細了。(真的很詳細!)
>> help GA_CVRP_optimize
GA_CVRP_optimize 針對 CVRP 問題的遺傳算法求解器
此 MATLAB 函數利用遺傳算法優化解決 CVRP 問題,支持動態圖實時顯示迭代過程的全
局最優解搜索下降進度,會在命令行窗口輸出提示信息。
[bestIndividual, minCost] = GA_CVRP_optimize( ...
OD_mat, numVehicles, demands, capacity, ...
popSize, maxIter, pc, pm)
[bestIndividual, minCost, iterPop, fitnessValues] ...
= GA_CVRP_optimize( ...
OD_mat, numVehicles, demands, capacity, ...
popSize, maxIter, pc, pm, ...
dynamic_plot ...
)
注意事項
1. 為了簡化問題的建模,採用整型數據編碼的形式。
2. 算法採用了精英策略,保存、記錄和返回歷代中的最精英個體及其適應度。
3. 交叉、變異過程採用了帶約束的交叉編譯過程,如果交叉變異產生的新的個體
無法滿足模型約束的要求,交叉、變異將不會發生。
4. 無法確保找到全局最優解。
輸入參數
OD_mat - 所有節點之間的 OD 矩陣。此處要求 OD 矩陣中的第一個節點是 CVRP
問題的配送中心節點,即 Depot 節點。
numVehicles - CVRP 問題中運載工具的數量
demands - CVRP 問題中各個顧客節點的需求量的一維向量
capacity - CVRP 問題中運載工具的容量限制
popSize - 遺傳算法的種群大小
maxIter - 最大迭代次數限制
pc - 交叉概率
pm - 變異概率
dynamic_plot - 一個 Bool 值,表示是否彈窗並動態繪製模型求解的下降過程
輸出參數
bestIndividual - 遺傳算法迭代產生的最優精英個體
minCost - 遺傳算法優化的結果,即 CVRP 問題中汽車最終行駛的總里程數
iterPop - 最終次迭代的種群
求解器支持在算法迭代過程中實時動態繪製下降過程,繪製效果如下圖所示。

遺傳算法中最小化路程的下降過程
輸出結果
算法的輸出結果如下圖所示,圖中使用不同的顏色標記了不同車輛的訪問路徑。取得極小化路徑長度為 815.29。
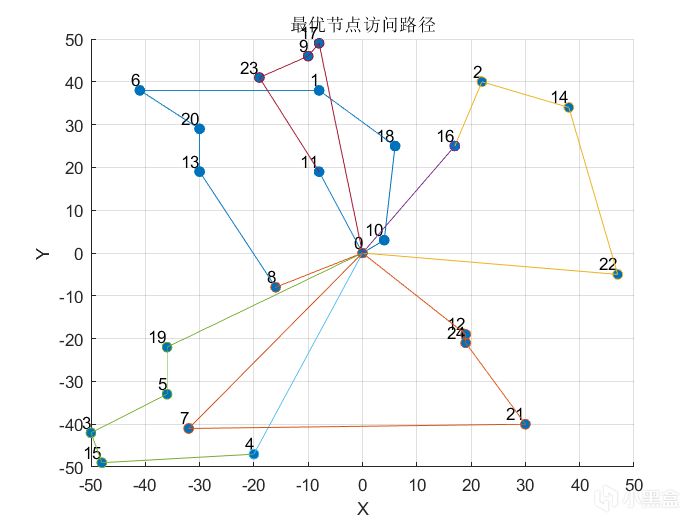
遺傳算法的優化結果
總結
代碼是根據自己的理解寫的,可能有諸多不成熟、不嚴謹的地方。如果您對於代碼有任何的改進建議,歡迎您提交 Pull Request 和 Issue。您的建議對我來說很重要。